AUTOMATIQUE
Automation, automatique, automatisation, automatismes, théorie des automates, cybernétique..., la variété même des vocables utilisés traduit la difficulté de définir précisément le contenu du substantif automatique .
Nous choisirons ici d’appeler automatisation l’art de rendre automatique un processus et automatique l’ensemble des méthodes permettant d’apporter des solutions à des idéalisations mathématiques de problèmes posés par l’automatisation, et visant à produire des méthodes concrètes pour la solution de ceux-ci, généralement sous la forme d’algorithmes numériques.
Cette définition restrictive présente l’avantage de délimiter un ensemble de méthodes et de résultats, de nature mathématique, qui, d’une part, ont une certaine perennité, et, d’autre part, sont assez universels et indépendants des applications.
En effet, l’automatique n’a pu devenir une science qu’en dégageant des modèles abstraits des problèmes d’automatisation. Cette abstraction même a eu pour conséquence de faire sortir largement l’automatique du cadre étroit de l’automatisation des processus industriels qui l’avait engendrée. Parmi les nouveaux domaines d’application, citons l’économie et la gestion, la géophysique et l’hydrogéologie, la biologie et la pharmacocinétique, la dynamique des populations et l’épidémiologie, etc.
Comme science de modèles mathématiques, elle ne peut éviter de traiter aussi de questions nées de la logique propre de la construction échafaudée, c’est-à-dire de science «fondamentale». Ainsi, il n’est pas douteux que l’automatique ait fait faire des progrès à certains domaines des mathématiques pures (en calcul des variations par exemple). Mais, dans sa nature même, l’automatique est une science appliquée.
À ce propos, un fait remarquable est que c’est un domaine où les mathématiques se sont révélées particulièrement pertinentes, permettant d’apporter des solutions efficaces à des problèmes concrets difficiles.
L’efficacité de l’outil mathématique n’est pas nouvelle tant qu’il s’agit d’«expliquer», voire de prédire, le comportement de la nature. Le fait assez nouveau est le pouvoir, ou plutôt l’ambition, de guider l’action qui a décuplé, en raison d’une mutation fondamentale de la nature même d’une partie des mathématiques. L’avènement des calculateurs, analogiques puis et surtout numériques, en permettant des calculs d’une complexité inconcevable auparavant, a fait des mathématiques une science opérationnelle , et non plus spéculative. La théorie des systèmes, qui est le cœur de l’automatique contemporaine, est une des premières constructions mathématiques conçues pour exploiter ce fait.
Une construction antérieure, plus hétéroclite, est la recherche opérationnelle. Aujourd’hui, les frontières tendent à s’effacer, et le passage des modèles statiques aux modèles dynamiques se fait par l’irruption des méthodes de l’automatique dans les domaines autrefois réservés de la recherche opérationnelle: gestion, planification économique, etc. Dans une autre direction, l’automatique se fond avec la théorie du signal, pour la double raison que la mise en œuvre en temps réel oblige l’automaticien a se préoccuper de ces questions, et que les modèles de la théorie des systèmes sont particulièrement bien adaptés pour les traiter.
Il ne faudrait pas en déduire qu’une théorie unifiée de tous les problèmes de décision est née. L’automatique est elle-même une collection de méthodes et de théories, avec une typologie très forte entre problèmes à état discret et problèmes à état continu.
1. Exemples
Automatique discrète
Les automatismes les plus simples sont les séquencements conditionnels. Considérons, à titre d’exemple, une machine devant percer une pièce mécanique qui lui est présentée par un porte-pièce mobile. La séquence à exécuter est définie de la façon suivante: – quand une pièce est déposée sur le porte-pièce, déclencher l’avancement de celui-ci et la mise en rotation du foret;
– quand le signal de fin de course du porte-pièce a été reçu, et quand le courant moteur du foret est à sa valeur nominale, déclencher l’abaissement du foret. Simultanément, déclencher une horloge;
– quand le signal de fin de course du foret a été reçu, ou quand l’horloge a atteint trente secondes, remonter le foret et arrêter son moteur.
La séquence pourrait se continuer avec émission de signaux de fin normale ou anormale de cycle, retrait du porte-pièce, etc.
On voit donc des actions qui doivent être prises quand un signal est présent (la première), ou quand plusieurs signaux sont présents simultanément (la deuxième), ou quand l’un ou l’autre de plusieurs signaux est présent (la troisième). Naturellement, des combinaisons plus complexes sont possibles. Cela doit être réalisé à l’aide de circuits logiques remplissant ces fonctions. Chacun de ces signaux (signaux reçus ou ordres donnés) peut être présent ou absent , ou encore l’affirmation «le signal est donné» prendre la valeur vrai ou faux . On a donc une logique binaire, dont on représentera souvent les valeurs par 1 et 0.
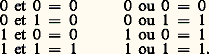
On peut ainsi développer une algèbre de ces opérations, appelée algèbre de Boole , qui indique comment les composer, étant admis que plusieurs technologies permettent de les réaliser physiquement.
Pourtant il est, dans la description ci-dessus, un signal un peu particulier, c’est celui de l’horloge. En pratique, on procédera en comptant des impulsions émises à intervalles réguliers. Cela suppose donc un dispositif qui se «souvienne» du nombre d’impulsions reçues, donc de mémoires. Ainsi, l’arrivée de l’impulsion de rang voulu déclenche le signal (ici, signal de relèvement du foret), alors que l’arrivée des impulsions précédentes n’avait provoqué aucune modification «externe» au compteur, mais en avait seulement modifié l’état «interne».
L’existence de mémoires, et d’un état interne de l’automatisme, apparaît dans de nombreux systèmes beaucoup plus complexes allant du dispositif de commande d’un ascenseur à mémoire aux ordinateurs. Ce sont là des systèmes à état discret. (L’état ne peut prendre qu’un nombre fini de valeurs, même si, dans le cas d’un ordinateur par exemple, ce nombre est très élevé.) On les appelle automates (ou machines ).
Si l’on appelle x (t ) la valeur de l’état à l’instant t , u (t ) l’ensemble des signaux d’entrée, y (t ) l’ensemble des signaux émis (ce peut être, par exemple, des vecteurs dont les coordonnées prennent les valeurs 0 ou 1), l’automate sera décrit par des équations de la forme:

Dans le cas où l’état ne peut prendre qu’un petit nombre de valeurs, il peut être commode de représenter l’automate à l’aide d’un graphe, dont chaque nœud représente une valeur possible de l’état, à laquelle est aussi associée une valeur de la sortie, et chaque arc une transition possible. On note sur chacun la valeur de l’entrée produisant cette transition.
Ainsi, un compteur dont l’entrée peut prendre les valeurs 0 et 1, signalant par l’émission d’un 1 l’occurrence du quatrième 1 en entrée a le graphe qui est représenté dans la figure 1.
Par contre, si on veut signaler les chaînes de quatre 1 successifs, le graphe sera celui de la figure 2.
La théorie des automates a connu un grand développement dans le cadre de l’automatique, un des problèmes de base étant de trouver le nombre minimal d’éléments mémoires requis, ainsi que leur arrangement, pour réaliser un automate spécifié par son comportement. L’objectif était bien sûr d’économiser ces composants. Aujourd’hui ce problème a pratiquement disparu. Les composants élémentaires disponibles sur le marché (et très bon marché) sont composés de milliers ou de dizaines de milliers d’éléments logiques. Ils effectuent des fonctions très complexes, ou sont eux-mêmes cet automate universel qu’est un ordinateur programmable. Le problème s’est donc déplacé: ce qui est cher n’est plus le composant, mais le temps passé par les ingénieurs à concevoir puis utiliser le système, et éventuellement les erreurs et le temps passé à les corriger. On s’oriente donc vers l’utilisation d’un matériel très surabondant du strict point de vue du nombre d’états nécessaires, mais facile à mettre en œuvre: le microprocesseur.
Ainsi, la frontière entre l’automatique et l’informatique s’estompe. Cela d’autant plus que la théorie des automates est le fondement de la théorie des langages [cf. INFORMATIQUE].
Des progrès ont été réalisés dans le domaine des langages utilisés pour spécifier un processus: langages graphiques, tels les réseaux de Petri, ou le Grafcet normalisé en France, ou langages de programmation en temps réel. Là de gros progrès restent à faire, malgré l’apparition de concepts de ce type dans le langage ADA par exemple.
Automatique continue
Le problème de base qui est à l’origine de l’automatique continue est celui de la régulation . Il s’agit, en agissant sur un système physique, de maintenir certaines grandeurs au voisinage de valeurs données, dites de consigne, en dépit des perturbations qui tendent à les déplacer.
Nous prendrons pour premier exemple le problème de maintenir l’attitude d’un vaisseau spatial en rotation autour d’un axe d’inertie (fig. 3). On souhaite maintenir près de zéro l’angle y entre l’axe du vaisseau et sa direction de consigne. On dispose pour ce faire de petites fusées de commande d’attitude susceptibles d’exercer un couple 臨 connu dans un sens ou dans l’autre. On veut s’en servir pour compenser les perturbations, telles que la pression de radiation solaire, qui tendent à écarter le vaisseau de la position souhaitée.
En notant I le moment d’inertie du vaisseau, et u le couple appliqué, l’équation du mouvement est donc:

(on note avec des points les dérivées successives par rapport au temps).
L’idée la plus simple, sans doute, est d’utiliser la loi de commande :

On se rend vite compte qu’elle présente l’inconvénient d’induire des oscillations peut-être excessivement rapides du vaisseau, mais surtout de conduire à l’utilisation continue des fusées de commande, et donc à l’épuisement rapide de leur carburant.
On peut l’améliorer en introduisant une bande morte de largeur 2 :

On peut représenter le comportement du système sous ces régulations (en négligeant les perturbations) sur un graphique en (y , face="EU Updot" 冷 ), qui fait apparaître des cycles limites (fig. 4). Pour la loi (4), si la vitesse v à laquelle on sort la bande morte est faible, alors le temps de parcours des arcs de paraboles, pendant lequel les fusées agissent, est court (4 vI / 臨 par cycle) par rapport à la durée du cycle (supérieure à 4 v). Si on veut en outre pouvoir réduire l’amplitude du cycle jusqu’à une valeur jugée acceptable, il faut aussi faire intervenir face="EU Updot" 冷 dans la loi de commande.
Pour élémentaire qu’il soit, cet exemple contient les ingrédients de base du problème de la régulation: une commande (ou entrée ), le couple, influence une observation (ou sortie ), l’attitude, à travers une relation dynamique (2). On a là un système dynamique , dit monovariable car on n’y prend en compte qu’une entrée et qu’une sortie. Les automaticiens ont coutume de symboliser cet objet par le diagramme ci-dessous:
C’est ce concept de système dynamique, en général multivariable (m entrées influencent p sorties, m et p supérieurs à un), qui est l’abstraction clef de l’automatique. Le même concept peut s’appliquer à de très nombreux systèmes physiques à temps, voire état, discret, comme en (1), ou continu comme ici. L’analyse mathématique de classes de tels systèmes a donc des applications dans tous les domaines où cette représentation est pertinente. Ainsi le système (2) peut-il aussi bien représenter le positionnement d’un chariot automoteur sur une voie, ou tout système où l’on commande l’accélération d’une variable, sans terme de frottement ni de rappel.
Le fait essentiel mis en évidence par cet exemple est que, pour réguler le système, il faut mesurer la sortie et choisir la commande en fonction de cette sortie. C’est ce qu’on appelle une commande en rétroaction (ou, de l’anglais, en feedback ) ou en boucle fermée , par opposition à une commande définie a priori, dite en boucle ouverte . On la symbolise par le diagramme de la figure 5, où l’on a en outre indiqué des perturbations additives v.
Un deuxième exemple de régulation va nous être fourni par le régulateur de Watt. Le problème est de maintenir constante la vitesse de rotation y d’une machine à vapeur, bien qu’elle entraîne les machines d’un atelier et supporte de ce fait une charge variable. On peut agir sur la position de la vanne de vapeur, représentée par u (qui sera par exemple la fraction de l’ouverture maximale).
Pour pouvoir mesurer la vitesse de rotation y à réguler, Watt utilise le célèbre dispositif à boules (fig. 6), dont le curseur se stabilise à une hauteur qui croît avec la vitesse de rotation de l’axe vertical qui le porte. Cela fournit une grandeur fonction monotone de y , qui permet, par l’intermédiaire d’un dispositif mécanique, d’agir sur la vanne d’alimentation.
Ici, il ne saurait être question d’agir, comme dans le premier exemple, par «tout ou rien». Manifestement, il faut ouvrir «un peu plus» la vanne quand la machine ralentit, et la refermer «un peu» quand elle accélère. Mais de combien? L’idée la plus simple est de repérer la position u c de la vanne pour laquelle la machine, sous une charge moyenne, tourne à la vitesse de consigne y c . Puis on dévie de u c d’une quantité proportionnelle à l’écart y 漣 y c , avec un gain k à choisir:

Cependant, on se convainc vite qu’aucune loi u = f (y ) ne peut maintenir la vitesse de rotation à y c pour des charges différentes. En effet, cette loi devrait, pour être correcte à charge moyenne, satisfaire comme (5) u c = f (y c ). Mais pour une charge plus grande, il faudrait avoir u 礪 u c , pour y = y c , ce qui est contradictoire.
Si la vitesse se stabilise pour une charge supérieure à la moyenne, ce sera donc à une valeur inférieure à y c , et d’autant plus proche que la pente de la fonction f sera grande (en valeur absolue), donc que k sera grand dans (5), ce qui aura aussi tendance à faire réagir le système plus vite. On dit alors que l’asservissement est «raide». Mais cela risque de produire des oscillations parasites – penser à l’exemple (2) –, voire de rendre le système instable, c’est-à-dire que l’amplitude des oscillations va augmenter jusqu’à ce que des limitations physiques entrent en jeu.
On voit qu’on peut remédier au premier inconvénient (le biais en valeur asymptotique) en ajoutant à (5) un terme intégral et au deuxième en ajoutant un terme dérivé , ce qui mène à la célèbre régulation P.I.D.:

De tels boîtiers, en technologie analogique (les grandeurs sont représentées par des tensions électriques) sont très répandus dans l’industrie.
Il faut remarquer que dans cette régulation, toujours en rétroaction, le compensateur est lui-même un système dynamique, en raison du terme intégral constituant une «mémoire» du passé. Remarquons aussi que la dérivée face="EU Updot" 冷 peut être difficile à évaluer si le signal est corrompu par un bruit de mesure à haute fréquence.
Cette régulation peut remplir sa fonction, si le système se stabilise. Mais comment répondre à cette dernière interrogation? Comment concevoir un meilleur régulateur si celui-ci n’est pas satisfaisant? Comment prendre en compte des systèmes multivariables (avec, par exemple, moins de commandes que de variables à réguler)? Comment s’accommoder des imprécisions de mesure? Pour répondre à ces questions, il faut manifestement disposer d’un modèle mathématique du système et, comme celui-ci risque d’être singulièrement plus compliqué que dans l’exemple (2), d’une méthodologie pour étudier ces modèles. De plus, il sera peut-être aussi nécessaire de disposer d’un «modèle» (par exemple statistique) des perturbations susceptibles d’agir sur le système ou de corrompre les mesures.
Les chapitres suivants sont destinés à donner un aperçu des constructions mathématiques qui ont été élaborées pour apporter des réponses à certaines de ces questions. Mais, auparavant, nous voulons aborder un vaste domaine d’applications qui joue un rôle très important dans le développement de l’automatique contemporaine, tant sur le plan de la réflexion théorique que sur celui des applications industrielles.
La robotique
L’automatique née de la théorie des systèmes répond très bien aux problèmes d’automatisation des processus continus et de communication (ainsi, nous l’avons dit, qu’à de nombreux problèmes de même structure logique issus d’autres domaines). Mais il reste tout le domaine de l’industrie manufacturière, caractérisée par de nombreuses opérations discontinues, impliquant des manutentions. Les industries d’assemblage en sont le type (automobile...). Deux voies complémentaires ont été poursuivies pour résoudre ces problèmes. La première consiste à remodeler profondément le processus de fabrication pour intégrer les transports, les usinages et les manutentions dans une conception globale, réduisant au minimum l’intervention d’opérateurs. C’est ce qu’on a appelé des «ateliers flexibles», car cette organisation nouvelle étant fondée sur des commandes par calculateurs, elle dépend de programmes qui peuvent être transformés pour modifier le fonctionnement de l’atelier. L’optimisation de ces ateliers pose aux mathématiciens appliqués des problèmes extrêmement difficiles, et encore largement ouverts.
La seconde voie consiste, schématiquement, non seulement à conserver l’organisation traditionnelle des chaînes de montage mais aussi à automatiser le poste de travail, à l’aide d’un outil qui, devant imiter le mouvement d’un homme, a parfois un caractère anthropomorphe, et qu’on appelle un robot.
Dans la génération actuellement industrialisée, ces robots ne sont guère que de remarquables manipulateurs programmables. Les problèmes d’automatique qu’ils posent reçoivent des réponses opérationnelles, sinon idéales, avec la théorie disponible: asservissements devant fonctionner avec des charges très variables suivant que le bras est chargé ou non, plié ou déplié... Ils permettent déjà de construire des objets (carrosseries d’automobile par exemple) différents mêlés sur une même chaîne. Le transporteur porte simplement un marquage qui peut être enregistré par l’outil de commande du robot, provoquant le déroulement du programme approprié.
Mais on vise une génération ultérieure où le robot disposera de capteurs beaucoup plus sophistiqués de son environnement, permettant une action fonction de circonstances non décrites en détail a priori. Un exemple type est la prise d’objets en vrac, à l’aide de capteurs optiques. À partir d’une image, les programmes doivent être capables de faire saisir une pièce du vrac au robot, et de la poser avec précision dans une position déterminée pour alimenter une machine d’usinage. D’autres capteurs sont aussi étudiés: proximètre, «peau» artificielle, etc. qui permettront au robot de se comporter de manière efficace (on dit «intelligente») dans des environnements très complexes.
2. Théorie des asservissements
À l’ère des calculateurs analogiques a correspondu la théorie des asservissements, qui traite des systèmes linéaires stationnaires, monovariables:

La réponse impulsionnelle h (t ) est nulle pour les valeurs négatives de t afin que le système soit causal: pour 精 礪 t , u ( 精) n’influence pas y (t ).
En passant aux transformées de Laplace de ces quantités, notées ci-dessous par les lettres majuscules correspondantes, et fonctions d’une variable complexe z , on obtient un produit ordinaire:

H (z ) est appelée la fonction de transfert du système. Grâce à cette forme simple, on obtiendra facilement la fonction de transfert de systèmes en cascade, en rétroaction, etc. Par exemple avec une rétroaction 漣 G (z ) on obtient:
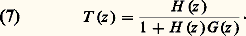
On sait que la transformée de Laplace de face="EU Updot" 冷 est zY (z ). Ainsi, on a une justification rigoureuse du calcul formel de Heaviside; le système:

admettra une fonction de transfert rationnelle:
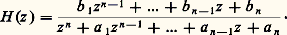
Les opérations de cascade, de mise en parallèle et de feedback ne font pas sortir du domaine des fonctions de transfert rationnelles. Leurs transformées inverses se calculent facilement par décomposition en éléments simples (ou à l’aide de tables).
On vérifie que le système (6) est stable (i.e. a une sortie bornée pour toute entrée bornée, et tendant vers zéro pour une entrée nulle) si et seulement si h est absolument sommable. En tenant compte du fait que h (t ) est nulle pour t négatif, cela se traduit par le fait que H (z ) doit être holomorphe pour les z à partie réelle positive, et donc, dans le cas rationnel, par le fait que les racines du dénominateur de H (le polynôme caractéristique) soient à partie réelle négative.
Les méthodes de synthèse de compensateurs sont fondées soit sur l’étude du polynôme caractéristique (critère de Routh) – mais cela est limité au cas où est explicitement connue une forme rationnelle de H (z ) –, soit le plus souvent sur le théorème de Nyquist. Celui-ci ne suppose connu que le lieu de Nyquist , qui est l’image dans le plan complexe de H (i 諸), 諸 捻 [ 漣 秊, + 秊]. (Ce lieu peut être obtenu de façon expérimentale, et est lié à l’impédance complexe des électriciens.)
Le théorème affirme que le système bouclé avec un gain négatif unitaire est stable si et seulement si le lieu de Nyquist entoure le point 漣 1 dans le sens positif un nombre de fois égal au nombre de pôles instables de H . Il est fondé sur le théorème de Cauchy et sur l’observation de la formule (7), qui montre que le théorème s’applique encore à un système muni d’un compensateur de fonction de transfert G, pourvu qu’on utilise le lieu de Nyquist du produit H (z ) G (z ).
Ainsi on pourra choisir le compensateur G (z ) pour qu’il déforme le lieu de la façon souhaitée, l’éloignant, par exemple, du point 漣 1.
D’autres critères graphiques ont été développés, fondés sur le même théorème mais utilisant d’autres représentations de H (i 諸). La plus répandue est peut-être le diagramme de Bode, constitué de deux courbes donnant, en fonction de Log 諸, l’une le (logarithme du) gain Log H (i 諸), l’autre la phase Arg H (i 諸). Ces deux quantités représentent respectivement le (logarithme du) rapport des amplitudes et le déphasage entre l’entrée et la sortie pour une entrée sinusoïdale de pulsation 諸 (d’où l’obtention expérimentale du lieu).
3. Théorie des systèmes
La théorie des systèmes linéaires (stationnaires) de dimension finie étudie des processus représentés par des modèles, à temps continu ou discret, de la forme:
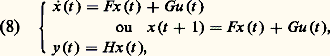
appelée représentation interne ; ici u (t ) est le vecteur des m entrées au temps t , x (t ) un élément de l’espace vectoriel des états (dont la dimension n est appelée dimension du système) et y (t ) le vecteur des p sorties; F , G et H sont des matrices de taille adéquate, dont les coefficients sont des nombres réels (indépendants du temps pour un système stationnaire). Si m = p = 1, le système est dit monovariable .
La résolution de ce système d’équations peut être effectuée aussi bien dans le domaine temporel , à partir d’un état initial x (t i ):

que dans le domaine fréquentiel , c’est-à-dire à l’aide des transformées de Laplace ou transformées en z pour le cas discret. La formule est la même pour les deux cas, et s’écrit (en prenant 0 pour instant initial, par stationnarité):
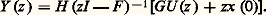
Si l’on échantillonne un système continu avec une période 精, considérant l’entrée constante entre deux instants d’échantillonnage successifs, il vient:
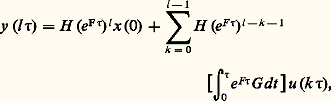
ce qui est la sortie du système discret défini par les matrices (e F size=1精 , 咽 精0e Ft Gdt , H ). Mais un système discret ne provient pas toujours de l’échantillonnage d’un système continu!
Un tel système évoluant à partir d’un état initial donné réalise une fonctionnelle affine entre les entrées et les sorties, linéaire si l’état initial est nul. Cette relation est caractérisée dans le domaine temporel par sa réponse impulsionnelle :

dont la convolution (continue ou discrète) avec l’entrée donne la sortie (cf. chap. 2) et dans le domaine fréquentiel, par sa fonction de transfert :

qui est une matrice rationnelle, ayant des valeurs propres de F pour pôles. Ce sont les représentations externes du système. On remarque aussi que:

L’étude des systèmes a mis en évidence le rôle essentiel joué par certains concepts:
– la complète accessibilité qui, quels que soient l’état initial du système et l’état final souhaité, garantit l’existence d’une fonction d’entrée amenant le système de l’un dans l’autre; pour un système linéaire stationnaire, continu ou discret, un critère est:

– la complète observabilité , qui garantit que les sorties d’un système correspondant à une même entrée, mais à deux états initiaux différents, ne sont pas des fonctions identiques; toujours dans les mêmes cas, un critère est:

– la stabilité correspond au fait que l’état du système tende vers zéro lorsque le temps tend vers l’infini, pour des entrées nulles. (Pour un système stationnaire, cela équivaut à ce que les valeurs propres de F aient leur partie réelle négative dans le cas continu, leur module inférieur à un dans le cas discret. Le système discret résultant de l’échantillonnage d’un système continu stable est donc lui-même stable.)
Si l’on sait expliciter la relation d’entrée-sortie induite par un système (8), la correspondance entre description interne et description externe n’est pas biunivoque: un changement de bases dans l’espace d’états, ou l’adjonction d’états non accessibles à partir de zéro, ou non distinguables de zéro par des observations de sortie, ne change pas la relation d’entrée-sortie.
Le théorème fondamental de la théorie des systèmes linéaires stationnaires affirme qu’une représentation interne est de dimension minimale parmi toutes celles ayant le même comportement d’entrée-sortie (les mêmes représentations externes) si et seulement si elle est complètement accessible et complètement observable (on dit alors qu’elle est canonique ), et elle est alors unique à un changement de base près dans l’espace des états.
La théorie de la réalisation affirme qu’un comportement externe donné admet une représentation interne de dimension finie si et seulement si la matrice de transfert est rationnelle, ou, de façon équivalente en termes de réponse impulsionnelle, si le rang de la matrice de Hankel (infinie) du système:
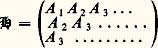
est fini (ce rang est la dimension n du système). Elle présente des liens étroits avec la théorie de la synthèse des réseaux passifs.
Le problème de la stabilisation d’un système linéaire a été résolu par le théorème suivant: il existe une loi de commande u = 漣 Cx (C : matrice de gains constante) telle que les valeurs propres de la matrice de dynamique F 漣 GC du système résultant prennent des valeurs fixées arbitrairement (en particulier stables) si et seulement si le système est complètement accessible. Si l’on n’a pas accès à l’état x du système et si ce dernier est complètement observable, on peut construire un système dynamique:

et choisir la matrice de gain K appliquée à l’innovation y 漣 y de manière que la différence entre l’état x et son estimée x tende vers 0 à un taux arbitrairement choisi; on peut alors utiliser l’estimée x à la place de x dans la loi de commande. On a alors une régulation par observateur-commandeur .
Il est possible de chercher un feedback d’états ou de sorties pour d’autres fins que la stabilisation du système: rejet de perturbations (c’est-à-dire faire en sorte que certaines entrées n’influent pas sur les sorties), découplage (chaque entrée influe sur une seule sortie), etc. Il a fallu pour essayer de résoudre ces problèmes faire une étude plus fine de la commandabilité du système et étudier les sous-espaces d’états accessibles par des trajectoires ne sortant pas de ce sous-espace: les sous-espaces de commandabilité , menant à ce qu’on appelle la théorie géométrique des systèmes linéaires.
Plus généralement, étant donné un système de fonction de transfert H (z ), se pose le problème de déterminer s’il existe un précompensateur interne, un externe et une boucle de réaction (tous trois étant des systèmes dynamiques et non plus de simples gains) tels que le système résultant:

ait une fonction de transfert T imposée en tout ou partie, et que les compensateurs soient stables et de dimension minimale. Les approches de ce problème reposent sur des factorisations de matrices rationnelles.
Le grand intérêt de la théorie des systèmes linéaires de dimension finie est qu’elle fournit une approximation opérationnellement satisfaisante pour une grande majorité de problèmes. Il existe bien sûr des phénomènes qui ne lui sont pas réductibles (changement de fréquence dans un poste de radio, mise en vibration d’une corde de violon par un archet...). Des efforts fructueux ont été faits pour étendre le cadre de la théorie.
La plupart des résultats restent valables si non seulement la variable temporelle mais aussi les valeurs des coefficients sont discrétisées (et sont par exemple des nombres entiers), ou si les équations différentielles ordinaires sont remplacées par des équations différentielles retardées (systèmes héréditaires). Parmi les systèmes non linéaires, les systèmes bilinéaires:
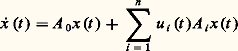
bénéficient eux aussi d’une théorie de la réalisation et de la stabilisation par boucle de réaction. Comme il a été démontré qu’un système non linéaire quelconque évoluant sur un intervalle de temps fini et y demeurant borné pouvait être approché arbitrairement près par un système bilinéaire de dimension adéquate (mais finie), il y a là un outil fort intéressant pour l’étude des systèmes non linéaires.
L’étude de systèmes non linéaires plus généraux mène à l’utilisation d’outils de géométrie algébrique pour les systèmes discrets, de géométrie différentielle (algèbres de Lie en particulier) pour les systèmes continus et en est au stade de la recherche.
4. Modélisation et identification
Le premier problème qui se pose à l’automaticien, chronologiquement, est d’obtenir un modèle du système à étudier. On distingue la modélisation, qui consiste à trouver les variables pertinentes et la forme des équations à utiliser, de l’identification, dont l’objet est l’évaluation numérique des paramètres apparaissant dans ces équations.
Le choix du modèle élaboré doit tenir compte de ce qu’on veut en faire, et exige, pour être bien mené, une bonne connaissance des propriétés des modèles mathématiques. On distingue les modèles de «connaissance», qui cherchent à être aussi précis que possible et doivent permettre de simuler au mieux le processus, par exemple pour tester plusieurs régulations, des modèles d’«action», destinés à permettre la conception d’une régulation. Une tendance moderne consiste à utiliser plusieurs modèles dans l’élaboration d’un même algorithme (cf. Grands systèmes , in chap. 5).
La phase de modélisation peut se limiter à la décision de retenir un système linéaire stationnaire. Cela est justifié, par exemple, quand on veut représenter de petits écarts du système autour d’un régime nominal. Une façon d’obtenir la réponse impulsionnelle consiste à superposer à la commande nominale une perturbation pseudoblanche (de spectre plat dans le domaine de fréquences d’intérêt). Les fonctions de corrélation croisée des sorties avec l’entrée perturbée sont alors les éléments correspondants de la matrice de réponse impulsionnelle. Dans d’autres cas, on peut obtenir directement les coefficients A i (systèmes aléatoires, déconvolution d’un système discret, etc.). La théorie des systèmes linéaires guide l’expérimentation et permet de passer de la description identifiée à celle qui est souhaitée.
D’une manière générale, le problème de l’identification peut se ramener à un problème d’optimisation. Pour une expérience d’entrée-sortie fixée, on choisit les paramètres à identifier pour minimiser une mesure (par exemple l’écart quadratique moyen) de l’écart entre la sortie observée et la sortie simulée par le modèle. Dans le cas non stationnaire, cela conduit à un problème de commande optimale.
Un cadre naturel, notamment pour l’identification en temps réel (cf. Commande adaptative , in chap. 6), est aussi fourni par la théorie du filtrage, linéaire ou non linéaire suivant la nature du modèle utilisé. Considérons par exemple le modèle monovariable suivant, où n est fixé (phase de modélisation):

où w (t ) est un bruit blanc de covariance connue. Regroupons les coefficients et les variables en deux vecteurs de façon suivante:

Si on admet pour modèle a priori de (t ) une marche aléatoire dont la covariance du bruit d’excitation est connue (elle peut être nulle pour représenter le cas constant), on arrive au système suivant, où la deuxième équation est une réécriture de (9):

À l’instant t , la matrice 兀 (t ) est entièrement connue. On peut donc estimer (t ) en temps réel à l’aide d’un filtre de Kalman non stationnaire (cf. chap. 6).
L’extension de cet algorithme au cas multivariable est élémentaire. Un inconvénient en est qu’alors la dimension minimale d’une réalisation interne de (9) n’est pas connue a priori, et peut varier avec les évaluations de . On peut avoir recours à des algorithmes de commande utilisant directement la forme (9) dite ARMA (autoregressive moving average ) vectorielle.
5. Commande optimale
Le problème type de la commande optimale est spécifié par un système dynamique, un ensemble de commandes admissibles:


où t 1 est le premier instant tel que p contraintes finales 﨏i (x ,t ) = 0 soient satisfaites. (Des cas particuliers sont t 1 = T donné et x (t 1) libre, ou fixé.) Ici, K et L représentent des coûts, final et de fonctionnement, ou l’opposé de gains, ou une pondération de tels éléments. Si, par exemple, 﨏 (x ,t ) = x 漣 x 1, K 令 0, L 令 1, on a le problème de transférer l’état de x 0 à x 1 en temps minimal.
Deux approches ramènent le calcul de la commande optimale à l’évaluation de la commande (x ,,t ) qui minimise le hamiltonien du problème:

Dans le principe du minimum de Pontriaguine, est calculé le long d’une trajectoire extrémale par la solution d’un problème aux limites:


(les 益i sont des paramètres à déterminer). On obtient une commande en boucle ouverte satisfaisant des conditions nécessaires d’optimalité.
En outre, pour toute commande u (.), les équations adjointes (10), initialisées en t 1 avec 益i = 0, permettent de calculer le gradient de J:

Ainsi, on peut soit chercher à résoudre directement le système (10) (11), soit généraliser les algorithmes de la programmation mathématique.
Dans la théorie de CarathéodoryBellman, apparaît comme le gradient en x de la fonction performance V (x ,t ) = minJ (x ,t ; u (.))|u (.) 捻 行, elle-même solution de l’équation de Hamilton-Jacobi Bellman:
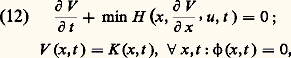
qui admet (10) (11) pour équations des caractéristiques. Pour V solution de (12), toute trajectoire engendrée par la commande en boucle fermée u (x ,t ) = (x , 煉V/ 煉x (x , t ), t ) et qui satisfait les contraintes finales est optimale.
Cette théorie s’étend à des cas plus compliqués (contraintes d’état, état discret...). Elle est utilisée dans sa version à temps discret, appelée programmation dynamique , régie par l’équation de Bellman, initialisée comme (12):

Un cas particulier intéressant est le cas linéaire quadratique:

t 1 est donné, x (t 1) libre. R (t ) est une matrice définie positive. Ce problème admet un infimum fini si et seulement si l’équation de Riccati :
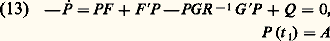

Il existe diverses extensions de la théorie, notamment au cas stationnaire: F , G , Q , R constantes, t 1 = 秊. Alors, si 﨏 = H H , et si (H , F , G ) est, par exemple, canonique, il existe une solution de la forme (14) stationnaire, où P est la limite pour t漣 秊 de la solution de (13) avec P(0) = 0. Une théorie algébrique très développée montre, par exemple, que les valeurs propres de la matrice F 漣 GR -1 G P du système bouclé optimal sont les valeurs propres stables de la matrice hamiltonienne:
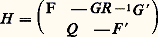
Le critère quadratique peut être un simple intermédiaire pour synthétiser une loi de commande stable: c’est la synthèse quadratique .
Commande des systèmes à paramètres distribués
La théorie ci-dessus peut être étendue aux systèmes gouvernés par des équations aux dérivées partielles. À chaque instant t , l’état y (t ) du système (on a changé de notation, adoptant y pour l’état, pour respecter la tradition de la littérature) est lui-même une fonction (c’est, par exemple, la distribution spatiale de température d’un corps 行, d’où l’expression «système distribué»). Un exemple simple est constitué par la commande de l’état thermique d’un corps 行. L’état y du système est gouverné par les équations:
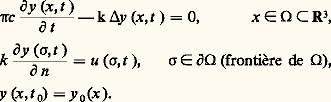
y (x , t ) représente la température au point x à l’instant t , u est la commande et représente le flux de chaleur (par unité de surface et de temps) entrant dans 行 au point 靖 de sa frontière, y 0 est la carte de température initiale, donnée, et 福, c et k sont des constantes physiques. On choisit un critère à minimiser. Par exemple:

Cela correspond à un compromis entre un coût de chauffage (ou refroidissement) et l’écart entre la température Zd désirée à l’instant t 1 et celle qui est obtenue. Il s’agit là d’un exemple «linéaire quadratique», et l’on peut définir l’analogue de l’équation de Riccati (13).
Une grande variété de problèmes peuvent se poser. La commande, par exemple, peut être répartie dans tout le domaine, ou, comme ci-dessus, à sa frontière. Elle peut intervenir en un nombre fini de points, ou même être de nature géométrique: localisation de ces points, forme du domaine, etc. De nombreux exemples apparaissent en thermique, électromagnétisme, biochimie, conception optimale de forme, etc.
Le calcul d’une solution se fait d’habitude par des méthodes d’état adjoint et de gradient. La recherche de commandes en boucle fermée se heurte à la très grande dimension du problème (on se ramène en effet au cas y (t ) 捻 Rn par une discrétisation convenable du problème).
Jeux différentiels
Une autre extension de la théorie de la commande optimale concerne les situations où plusieurs agents agissent sur le même système, chacun souhaitant minimiser son propre critère. Comme en théorie classique des jeux, il faut d’abord définir ce qu’on appelle une solution. Nous ne reprendrons pas la discussion des différents concepts d’équilibre. Ce sont les mêmes qu’en théorie des jeux, parfois un peu enrichis par la possibilité de faire agir les joueurs dans un ordre ou un autre à chaque pas de temps (notamment en temps discret).
Pour simplifier l’exposé, nous nous limiterons ici au cas le mieux résolu: jeu à deux joueurs (u et v) et somme nulle, et au concept de solution de point selle:
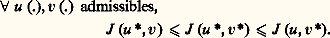
Donc u veut minimiser le critère et v le maximiser. Cela peut représenter une situation de conflit, comme dans les jeux de poursuite ou en temps minimax (K = 0, L = 1, t 1 = «capture»). Mais ce peut aussi être un problème de commande (par u ) en présence de perturbations (v), où l’on cherche le meilleur coût garanti possible.
La difficulté essentielle vient du fait qu’il faut, de manière cruciale, tenir compte de l’information disponible aux joueurs au cours de la partie sur les actions passées de leur adversaire. Ainsi, en général, il n’existera pas de point selle en boucle ouverte, mais seulement en boucle fermée (ou en stratégies u = 﨏(x ,t ), v = 祥(x ,t )). L’obligation de considérer des stratégies ajoute des problèmes techniques concernant l’existence d’une solution à l’équation différentielle, suivant le choix des ensembles de stratégies admissibles.
Le fondement de l’étude, théorique et pratique, de ces jeux est la version à deux joueurs de la théorie de Carathéodory, et de l’équation de Hamilton-Jacobi, qu’on appelle alors équation d’Isaacs . Une grande part de la théorie est consacrée à l’étude des singularités de cette équation, notamment d’hypersurfaces de discontinuité du gradient de la fonction valeur, phénomène qui ne se produit pas en commande optimale.
Le cas linéaire quadratique donne encore lieu à une théorie complète, mais seulement plus compliquée qu’en commande: l’existence d’une solution à l’équation de Riccati associée est une condition suffisante mais non nécessaire d’existence d’un point selle.
Grands systèmes
Les préoccupations de l’automatique issues de la régulation de processus comportant quelques entrées et quelques sorties ont évolué vers la conduite de vastes ensembles technologiques ou économiques dont les grands réseaux de distribution ou de service (électricité, eau, gaz, télécommunications, réseaux d’ordinateurs) ou les ateliers flexibles sont des exemples typiques. Elle s’est trouvée confrontée à de nouvelles questions pratiques, mais aussi théoriques, qui rejoignent par certains côtés celles de la recherche opérationnelle, de l’analyse numérique et de l’économie mathématique, et qui sont loin d’être toutes résolues aujourd’hui.
Il faut souligner l’extrême importance que revêt la notion d’optimisation dans ces grands systèmes: en effet, des gains de quelques pour-cent peuvent se traduire, en valeur absolue, par des économies considérables. Aussi les premiers résultats ont porté sur l’optimisation déterministe de ces systèmes par des méthodes de décomposition et coordination . Il s’agit de ramener l’optimisation globale du système considéré comme l’interconnection de plusieurs sous-systèmes à celle de l’optimisation indépendante de ces sous-systèmes, la poursuite de l’optimum collectif étant assuré par l’action (itérative) d’un niveau hiérarchique supérieur appelé coordonnateur . En ramenant ainsi l’optimisation du tout à celle des parties, on tente de surmonter les problèmes de taille (grand nombre de variables, de contraintes, etc.), mais un autre avantage important est de pouvoir adapter à chaque sous-problème une méthode spécifique de résolution.
À cause des deux niveaux d’optimisation locale et de coordination, on parle de commande hiérarchisée mais, comme les décisions optimales sont élaborées finalement par la résolution des sous-problèmes, on parle aussi de décentralisation . Ce dernier terme ne prend cependant tout son sens que dans une situation non déterministe, lorsque l’information en temps réel n’est pas centralisée auprès d’un décideur unique, par exemple lorsque la dispersion géographique du système rend cette centralisation trop coûteuse, voire impossible. On rejoint alors le cadre de la théorie des équipes (cf. chap. 7).
Du fait de la formulation de sous-problèmes solubles indépendamment les uns des autres, on débouche aussi sur une certaine forme de calcul parallèle et, de là, sur les questions d’architecture spécialisée d’ordinateurs (réseaux, machines multiprocesseurs, etc.).
Complémentaire à l’idée de décomposition est l’idée d’agrégation. Il s’agit là de scinder l’optimisation globale en problèmes à court terme et à long terme et d’adapter à chaque horizon d’optimisation un modèle différent. Ainsi dans l’optimisation à long terme, on tentera de simplifier la représentation de phénomènes dynamiques rapides transitoires ou périodiques. On aboutit ainsi à des modèles où le nombre de variables d’état est réduit. Sur le plan mathématique, ces techniques s’appuient sur la théorie des perturbations singulières et sur celle de l’homogénéisation .
6. Traitement du signal
Les mesures faites sur un processus sont toujours plus ou moins entachées d’erreurs, dues aux capteurs et à la transmission. De même, dans un système de télécommunication, le signal reçu a été perturbé par le canal et on cherche à récupérer le signal d’origine. D’où la nécessité de «traiter» le signal reçu.
Dans les problèmes de commande, dans de nombreux problèmes de télécommunication, on veut le signal amélioré en temps réel . C’est-à-dire que seuls sont disponibles pour déterminer le signal traité à l’instant t les signaux reçus jusqu’à cet instant. Ainsi, le processus même de traitement est un système dynamique, dont l’entrée est le signal reçu (éventuellement multivariable) et la sortie le signal traité. (On se limitera souvent à un traitement linéaire, utilisant la théorie des systèmes linéaires.) Autrefois, ce traitement était effectué par un dispositif électronique, appelé filtre , et le problème de la réalisation physique des filtres a donné naissance à la théorie de la réalisation. Aujourd’hui, il est plus souvent effectué par un ordinateur, donc aussi en temps discret. On a conservé le nom de filtre à l’algorithme mis en œuvre, la théorie de la réalisation fournit toujours un algorithme simple (de type (7)), à partir d’une spécification de comportement externe linéaire.
Les liens entre un signal continu et le même signal échantillonné font aussi partie de la théorie du signal. Le théorème de Nyquist indique que, pour ne pas perdre d’information, il faut échantillonner le signal à une fréquence double de la plus haute fréquence présente dans ce signal (cf. théorie du SIGNAL). De même, l’effet de la quantification et du choix du codage relève de la théorie de l’information (cf. théorie de l’INFORMATION).
Pour pouvoir améliorer le signal reçu, il faut avoir des connaissances a priori sur le signal que l’on aurait dû recevoir, à savoir un modèle de ce signal. Un modèle traditionnel typique, bien que presque toujours implicite, est qu’il ne doit comporter que des fréquences «assez basses», et que le bruit, lui, est à haute fréquence. Il faut donc lisser le signal (fig. 7).
Le filtre qui réalise cette opération est un passe bas idéal ayant un gain unité pour 諸 麗 諸0, et nul pour 諸 礪 諸0. Aucune fraction rationnelle n’ayant ce graphe, on ne sait pas réaliser un tel filtre, mais on l’approche au mieux par des filtres de dimension finie (de 5 à 10 couramment).
Les problèmes d’estimation d’un signal à partir d’un autre (le signal bruité) ont pu être quantifiés en prenant des modèles stochastiques: on admet que chaque signal est une réalisation d’un processus stochastique, supposé ergodique pour qu’on puisse mesurer ses propriétés statistiques. Ainsi peut-on calculer des espérances mathématiques.
Dans le filtre de Wiener , on suppose connue la fonction d’autocorrélation du signal reçu (elle peut être mesurée) et la fonction de corrélation croisée entre le signal à estimer et le signal reçu (qu’on peut déduire de la précédente si on considère, par exemple, que le signal reçu est la somme du signal à estimer et d’un bruit indépendant d’autocorrélation connue). On peut alors calculer la fonction de transfert du filtre optimal. La formule, assez compliquée, n’est guère utilisable que pour des signaux scalaires à spectre rationnel.
Dans le filtre de Kalman , on prend pour modèle du signal reçu la sortie d’un système linéaire excité par un bruit blanc:
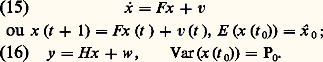
Ici (vw) est un bruit blanc gaussien discret ou continu suivant la nature du modèle utilisé, de densité spectrale connue (nous écrirons les formules pour le cas ou elle est diagonale par bloc: diag[Q,R ]). Alors, x (t ) = E (x (t )|y (s ), s 麗 t ) est donné par:

où K (t ) et la covariance d’erreur P (t ) se calculent, dans le cas continu, à l’aide d’une équation de Riccati:
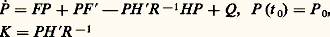
(on note la dualité avec les formules (13) et (14) de la commande optimale linéaire quadratique), et avec des formules analogues dans le cas discret (duales de celles du problème de commande discret):

La théorie des systèmes nous apprend que tous les processus à spectre rationnel peuvent être représentés par un modèle de type (15) (16) ci-dessus (sans que les variables x aient nécessairement un sens physique). Donc le champ d’application du filtre de Kalman est celui du filtre de Wiener, étendu au multivariable et surtout au non stationnaire. Dans le cas stationnaire, il converge vers une représentation interne du filtre de Wiener.
Enfin, la théorie de la réalisation gaussienne markovienne montre comment retrouver H ,F ,Q et R (et la covariance croisée S de v et w) à partir de la seule fonction d’autocorrélation de y (qui peut se mesurer). Il y a une infinité de modèles possibles, répartissant différemment l’énergie du bruit entre v et w. Mais tous ont la même estimée filtrée y = Hx .
Les modèles de signal consistant en la sortie d’un système linéaire excité par un bruit blanc sont très utilisés, notamment en économétrie (séries temporelles) et en télécommunications (égalisation, suppression d’écho...). Différentes techniques ont été mises au point pour identifier le modèle. Elles utilisent souvent la forme autorégressive à moyenne mobile , ou ARMA, qui dérive directement de la représentation fonction de transfert d’un système discret. Prenons le cas scalaire. Le système Y (z ) = H (z ) U (z ) avec:
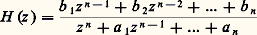
peut être écrit en multipliant par le dénominateur et en revenant dans le domaine temporel:

En prenant pour u (t ) un bruit blanc, c’est un modèle ARMA de y (t ). On peut aussi l’utiliser dans le cas multivariable, avec des coefficients a i et b i matriciels, correspondant à la forme fraction matricielle de la fonction de transfert: H (z ) = a -1 (z ) b (z ), a (z ) et b (z ) polynômes matriciels, de plus en plus utilisée en théorie moderne des systèmes.
Ces algorithmes (et donc cette forme de modèle) sont aussi utilisés maintenant en commande adaptative (cf. infra ).
Le problème du filtrage non linéaire est beaucoup plus difficile. Il impose de propager toute la loi de distribution conditionnelle de l’état (estimé) et manipule donc des systèmes distribués. (Le problème de l’approximation numérique du filtre, soit par discrétisation, soit par une approximation théorique par des filtres de dimension finie, a fait l’objet de recherches actives.) Un certain nombre de problèmes, comme la démodulation de phase, entrent typiquement dans ce champ.
Il faut enfin mentionner des développements vers le traitement des images, qui peuvent être considérées comme un signal où le temps est de dimension deux. On utilise de nombreux concepts issus de la théorie classique. Il faut aussi, par exemple en télévision, considérer des suites d’images corrélées les unes aux autres. Ces traitements exigent des systèmes numériques ayant des débits d’information considérables.
7. Commande stochastique et adaptative
Commande stochastique et théorème de séparation
Nous nous limiterons ici à une formulation à état continu et à temps discret (le cas du temps continu ferait appel à la théorie des équations différentielles stochastiques et le cas du temps et de l’état discrets, à celle des chaînes de Markov). Dans ce cadre, le problème s’énonce:

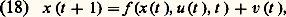
v étant un bruit blanc gaussien. Le symbole E représente l’espérance mathématique mais il ne prend de sens que lorsque l’on a précisé comment u et donc x dépendent des variables aléatoires introduites initialement dans le modèle. Cela revient à préciser la classe des stratégies (ou commandes en boucle fermée) sur laquelle l’optimisation est conduite. Ces stratégies seront toujours causales, c’est-à-dire ne dépendant que des observations passées. On distingue le cas de l’observation parfaite (on observe x t exactement) et celui de l’observation imparfaite, voire incomplète:

où y est un vecteur d’observations de dimension éventuellement plus petite que celle de x , et w est un autre bruit blanc.
Le cas de l’observation parfaite est évidemment plus simple et les conditions d’optimalité prennent la forme de l’équation de Hamilton-Jacobi-Bellman issue de la programmation dynamique stochastique (extension du cas déterministe). Sur le plan de la résolution numérique, on souffre donc des mêmes limitations (dimension de x limitée à trois).
Dans le cas général, la grande difficulté vient du fait que l’information contenue dans l’observation y t dépend des stratégies utilisées avant t , d’où le phénomène connu sous le nom d’effet dual de la commande stochastique: un moyen indirect pour minimiser (17) est de chercher à améliorer la qualité des observations futures. Sur le plan mathématique, le problème se ramène à celui de la commande d’un système stochastique de dimension infinie: le filtre non linéaire qui propage la densité de probabilité de x t conditionnelle aux observations jusqu’à t , le critère (18) pouvant manifestement s’écrire en fonction de celle-ci.
Il est cependant un cas qui échappe à cette complexité: c’est le cas où la dynamique (18) et l’observation (19) sont linéaires et le critère (17) est quadratique. Les problèmes de filtrage et de commande optimale peuvent alors être résolus séparément (d’où le nom de théorème de séparation ). La stratégie optimale, consiste à remplacer x par l’estimée x , fournie par le filtre de Kalman, dans la solution du problème déterministe (cf. supra ). On constate ici l’absence d’effet dual, la covariance de la loi conditionnelle (gaussienne) de x t (fournie par le filtre de Kalman) étant indépendante de la loi de commande (linéaire) utilisée.
Commande adaptative
Cette théorie est une tentative d’aborder, par des techniques linéaires d’estimation et de commande, la régulation de systèmes dont le modèle ou l’environnement sont mal connus a priori ou susceptibles de varier de façon imprévisible. Cette situation peut résulter par exemple de la prise en compte d’un modèle linéaire pour un processus non linéaire (le modèle linéaire étant vu comme une linéarisation autour d’un point de fonctionnement variable).
Il existe des formulations déterministes et stochastiques de la théorie qui tendent à se rejoindre aujourd’hui. On pourrait considérer les paramètres inconnus du modèle comme des variables d’état supplémentaires dont la dynamique peut ou bien refléter une connaissance a priori de leur évolution, ou bien être simplement une marche aléatoire. Mais on sort alors du cadre linéaire. Dans une formulation stochastique, on hériterait donc des difficultés rencontrées ci-dessus. On sépare donc artificiellement à chaque instant la phase de recalage du modèle (estimation des paramètres) et celle de calcul de la commande, utilisant le modèle recalé, d’où à chaque fois un problème linéaire (d’estimation ou de commande). Cela constitue l’approche indirecte . Dans l’approche directe , ce sont les paramètres de la loi de commande que l’on recale directement. La seule justification de ces approches est la démonstration a posteriori de la stabilité des schémas ainsi construits. Cette question fait appel aux théories de l’hyperstabilité et de l’approximation stochastique .
Du point de vue pratique, l’utilisation des techniques linéaires doit permettre celle des microprocesseurs. La commande adaptative trouve son application dans les cas de régulation industrielle difficiles tels que la synchronisation des turbo-alternateurs sur le réseau électrique en cas de perte de certaines lignes, la commande de systèmes mécaniques en robotique dans des conditions de charge variable, etc.
Cas de structures d’information non classiques
Dans le cadre général de la commande stochastique, on désigne ainsi les situations où plusieurs décideurs agissent sur un système avec des informations différentes (commande décentralisée) ou bien le même décideur physique agit à des instants successifs sans pouvoir utiliser toutes ses observations passées. Dans une situation coopérative par exemple (minimisation par l’ensemble des décideurs d’un même critère – cas de la théorie des équipes ), cela ouvre la possibilité pour les décideurs en amont d’améliorer par le choix de leur stratégie l’information contenue dans les observations des décideurs en aval. Ce phénomène de «signalisation» via la dynamique du système est analogue à celui de l’effet dual rencontré plus haut et peut conduire à des stratégies très non linéaires même dans le cadre linéaire-quadratique-gaussien.
Dans ce cadre, une condition suffisante pour que les stratégies optimales restent linéaires est que chaque décideur ait au moins toute l’information qu’ont ceux dont l’action influence ses observations (ce qui rend l’effet de «signalisation» inutile).
Dans le cas général, on ne sait généralement pas calculer les stratégies optimales et on ne dispose pas encore de conditions nécessaires ni suffisantes d’optimalité sauf dans certains cas plus particuliers.
Étant donné ces difficultés, ce type de question a aujourd’hui un intérêt plus théorique que pratique. Cependant, la situation simple d’un système émetteur-récepteur où l’émetteur code un message qui est corrompu par un bruit de transmission avant d’être reçu et décodé par le récepteur entre dans ce cadre. Le but est en effet de minimiser l’écart quadratique moyen entre les messages avant codage et après décodage par le choix de stratégies optimales de codage et décodage.
automatique [ ɔtɔmatik ] adj. et n.
• 1751; de automate
I ♦ Adj.
1 ♦ Physiol. Qui s'accomplit sans la participation de la volonté. Mouvement, réflexe automatique. ⇒ inconscient, involontaire , machinal, mécanique, spontané. Les gestes automatiques du somnambule. — L'écriture automatique des surréalistes.
2 ♦ (1839) Cour. Qui, une fois mis en mouvement, fonctionne de lui-même; qui opère par des moyens mécaniques. Appareil automatique. Boîte de vitesse automatique (opposé à mécanique), et par ext. voiture automatique. Distributeur automatique. Téléphone automatique. Pilote automatique. Signaux automatiques. Arme automatique, dans laquelle la pression des gaz de combustion est utilisée pour réarmer. — Traduction automatique.
3 ♦ (1878) Fig. Qui s'accomplit avec une régularité déterminée. « Nous avons un système de relèvement automatique des salaires quand le coefficient du prix de la vie augmente » (Maurois). Prélèvements automatiques sur un compte chèque.
♢ Fam. Qui doit forcément se produire. ⇒ forcé, sûr. Chaque année, à l'automne, il tombe malade, c'est automatique.
II ♦ N. m. Pistolet automatique. ⇒ browning.
♢ Téléphone automatique, sans intervention de standardiste. « Une dame des P. T. T. qui tardait à lui expliquer le fonctionnement de l'automatique dans le Var » (Sagan).
III ♦ N. f. Sc. Ensemble des disciplines scientifiques et des techniques utilisées pour la conception de la commande et du contrôle des processus. ⇒ cybernétique, informatique, robotique; asservissement.
⊗ CONTR. Conscient, délibéré, intentionnel, médité, prémédité, réfléchi, volontaire.
● automatique adjectif (de automate) Qui fonctionne par des moyens mécaniques sans intervention humaine : Fermeture automatique. Se dit d'un geste qui s'exécute sans la participation de la volonté ; machinal. Qui s'accomplit en vertu de règles fixées d'avance ou d'un enchaînement inéluctable : À cet âge, la mise à la retraite est automatique. ● automatique (difficultés) adjectif (de automate) Registre Au sens d'«inévitable», le mot est familier. Recommandation Préférer les équivalents fatal, inéluctable, inévitable : les rumeurs de dévaluation font s'effondrer les cours, c'est inévitable (plutôt que : c'est automatique). ● automatique (expressions) adjectif (de automate) Arme automatique, arme dans laquelle la force produite par les gaz de combustion de la poudre effectue à la place du tireur la plupart des opérations nécessaires à son fonctionnement. Écriture automatique, procédé d'écriture qui est à la base de la pratique littéraire du surréalisme. ● automatique (synonymes) adjectif (de automate) Qui fonctionne par des moyens mécaniques sans intervention humaine
Synonymes :
- mécanique
Se dit d'un geste qui s'exécute sans la participation de...
Synonymes :
- machinal
- mécanique
- réflexe
Contraires :
- délibéré
- réfléchi
Qui s'accomplit en vertu de règles fixées d'avance ou d'un...
Synonymes :
- systématique
Contraires :
- aléatoire
- douteux
- hypothétique
● automatique
nom masculin
Téléphone automatique.
Pistolet automatique.
Moulinet pour la pêche à la mouche, dont la rotation du tambour est assurée par un ressort puissant.
● automatique
nom féminin
Science et technique de l'automatisation, groupant l'ensemble des disciplines théoriques et technologiques intervenant dans la conception, la construction et l'emploi des systèmes automatiques.
automatique
adj. et n.
rI./r adj.
d1./d Qualifie les mouvements du corps humain exécutés sans l'intervention de la volonté, de la conscience.
d2./d Qualifie un dispositif qui exécute de lui-même certaines opérations définies à l'avance. Distributeur automatique de café.
|| Fig. Qui s'accomplit lorsque certaines conditions sont remplies. Une mise à la retraite automatique.
rII./r n. f. Science qui étudie les automates.
rIII/r n. m.
d1./d Pistolet automatique.
d2./d Système de liaison téléphonique automatique.
⇒AUTOMATIQUE, adj. et subst.
A.— Adjectif
1. [En parlant de l'activité de l'homme]
a) [Sans idée d'itération] Qui s'accomplit d'une manière inconsciente, sans la participation directe de la volonté ou de l'intelligence :
• 1. On peut établir en général, que, dans toutes les affections dites nerveuses, il y a des irrégularités plus ou moins fortes, et relativement à la manière dont les impressions ont lieu, et relativement à celle dont se forment les déterminations, soit automatiques, soit volontaires.
CABANIS, Rapports du physique et du moral de l'homme, t. 1, 1808, p. 425.
• 2. Il [Quinault] ne répondit pas un mot et quitta la pièce d'un pas automatique, hébété, dompté, sans trouver dans tout son répertoire une attitude à prendre pour couvrir cette piteuse sortie...
P. BOURGET, Conflits intimes, 1925, p. 108.
SYNT. Acte, comportement, geste, manière, mouvement, réaction, réflexe automatique.
Rem. Adverbialement (arg.) :
• 3. ... j'attrape un pavé, un gros... Je l'amarre à mon truc... Je regarde bien encore autour... J'agrafe tout le fourbi à deux poignes et je le balance en plein jus... Le plus loin que je peux... ça a pas beaucoup fait de bruit... J'ai fait ça automatique.
CÉLINE, Mort à crédit, 1936, p. 504.
— Spéc., LITT. Écriture automatique. Procédé utilisé par les surréalistes dans l'art de la composition poétique et consistant à écrire sous la dictée non contrôlée de l'esprit. Synon. plus rare automatisme :
• 4. — (...) Dans le temps, son frère Benjamin et lui ont pratiqué ce qu'on appelle l'écriture automatique. On obtient des rencontres de mots extraordinaires, des images bouleversantes. Il suffit de se droguer un peu pour que le geste soit assez rapide, que la pensée ne rattrape pas la vision... Quelles drogues? Alcool, café, puis toutes les autres, naturellement, jusqu'aux plus fortes, si l'on veut atteindre au génie...
ABELLIO, Heureux les pacifiques, 1946, p. 320.
b) [Avec fréquemment une idée de répétition, en parlant d'un événement, d'une action] Qui doit obligatoirement se produire, ou intervenir de façon prévisible, voire à intervalles réguliers. L'avancement automatique :
• 5. L'Allemagne, tenue par son traité de 1879 avec l'Autriche, est nécessairement amenée à mobiliser contre la Russie... Or, cette mobilisation forcerait la France à tenir les engagements qu'elle a pris envers la Russie, et à mobiliser immédiatement contre une Allemagne menaçant notre alliée... C'est automatique. ...
R. MARTIN DU GARD, Les Thibault, L'Été 1914, 1936, p. 356.
2. [En parlant d'objets, de mécanismes, d'appareils divers] Qui exécute un programme pré-établi d'opérations, sans intervention humaine directe :
• 6. Elle changea de métro dans un état d'égarement, horrifiée par ces dédales, ces courses vers un portillon automatique qui se ferme sous votre nez, ces portillons qui vous manœuvrent comme un bétail, comme si vous étiez un troupeau de porcs que sériaient des machines, dans une usine d'Amérique...
MONTHERLANT, Les Jeunes filles, 1936, p. 985.
• 7. Ce robinet doit être ouvert lorsque le régulateur est fermé. Sa commande est automatique ou manuelle suivant le cas.
M. BAILLEUL, Notions de matériel roulant des ch. de fer, 1951, p. 49.
SYNT. Arme, distributeur, embrayage, fermeture, téléphone automatique.
— Spéc. Traduction automatique. Méthode de traduction de textes qui s'effectue par l'intermédiaire d'ordinateurs :
• 8. À côté des langages documentaires, intermédiaires entre les utilisateurs et les auteurs de documents, il existe depuis quelques années, des tentatives de constitution de langages intermédiaires, très imparfaits, destinés à la traduction automatique entre langues naturelles.
M. COYAUD, Introd. à l'ét. des lang. documentaires, 1966, p. 18.
B.— Subst. (correspond à l'emploi adj. A 1)
1. Masc. (cour., le subst. est sous-entendu)
a) L'automatique. Téléphone qui ne nécessite pas l'intervention d'opérateurs :
• 9. ... Jacques sortit un bout de papier et y nota gravement le numéro de téléphone. Puis on se sépara. Et Jacques s'éloigna bien décidé : jamais il ne ferait par sept fois subir au cadran d'un automatique les rotations d'amplitudes diverses correspondant aux trois lettres et aux quatre chiffres de l'appel indiqué.
QUENEAU, Loin de Rueil, 1944, p. 144.
b) Un automatique. Pistolet, revolver.
2. Fém. ,,Science visant l'emploi d'une machine où l'intervention humaine est limitée à la préparation préalable, intellectuelle et matérielle, d'un programme incorporé à la machine qui le suivra seule, en le modifiant d'elle-même s'il y a lieu, par des décisions logiques conditionnées par les circonstances de déroulement des opérations`` (Électron. 1959).
PRONONC. :[ ] ou [
] ou [ -]. PASSY 1914 note [
-]. PASSY 1914 note [ -] et DUB. [oto-].
-] et DUB. [oto-].
 ] ou [
] ou [ -]. PASSY 1914 note [
-]. PASSY 1914 note [ -] et DUB. [oto-].
-] et DUB. [oto-]. ÉTYMOL. ET HIST. — 1. 1751 physiol. (M. Tarin ds Encyclop. : [...] se dit des mouvemens qui dépendent uniquement de la structure des corps, & sur lesquels la volonté n'a aucun pouvoir); 2. a) 1859 (REYBAUD, Et. sur le régime des Manufactures, Lyon [Aperçu historique], p. 121 : Même avant Vaucanson, et en 1678, l'officier de marine de Gennes avait trouvé et soumis à l'Académie des sciences un système qui assujetissait les divers organes du métier à tisser à des mouvements purement automatiques, pp. 126-128. En simplifiant le métier à tisser, Jacquart supprimait l'emploi des bras parasites; là où il fallait trois hommes autrefois, il n'en laissait qu'un d'occupé [...] Parallèlement à l'invention de Jacquart, il en est une autre qui a eu ses origines en France, mais qui lui a échappé pour n'y revenir que plus tard, c'est celle du tissage mécanique ou automatique. L'idée en existait dans les appareils de Gennes et de Vaucanson, dans le dernier surtout [...] Nous avions précédé l'Angleterre dans la découverte, nous l'avons suivie dans l'application. Des machines automatiques sont venues tisser nos cotons d'abord, puis nos laines, nos lins et enfin nos soies); b) av. 1872 id. « relatif aux automates » (Th. Gautier ds Lar. 19e : Vous voyez là des pièces automatiques que n'aurait pas désavouées Vaucanson).
Dér. de automate; suff. -ique.
STAT. — Fréq. abs. littér. :364. Fréq. rel. littér. : XIXe s. : a) 89, b) 214; XXe s. : a) 537, b) 1 033.
BBG. — AGRON (P.). La Fin d'un monstre : automation. Vie Lang. 1957, pp. 12-13. — BADER-TH. 1962. — BAUDHUIN 1968. — BOUILLET 1859. — BURN. 1970. — CHESN. 1857. — COLAS-CAB. 1968. — CROS-GARDIN 1964. — Électron. 1959. — Électron. 1963-64. — FOULQ.-ST-JEAN 1962. — GALL. 1955, p. 37, 284. — GUILB. Aviat. 1965 (s.v. automate). — LAL. 1968. — LHOSTE-PÈPE 1964. — LITTRÉ-ROBIN 1865. — NOËL 1968. — NYSTEN 1814. — PIÉRON 1963. — PRIVAT-FOC. 1870. — SIZ. 1968. — SOÉ-DUP. 1906. — TEZ. 1968.
automatique [otomatik; ɔtɔmatik] adj. et n.
ÉTYM. 1751; de automate.
❖
———
I Adj.
1 Qui s'accomplit sans la participation de la volonté. || Mouvement, réflexe automatique. ⇒ Inconscient, involontaire, machinal, mécanique, spontané. || Marche automatique du nouveau-né. || Les gestes automatiques du somnambule.
1 (…) le lent et minutieux travail (de recherche dans sa mémoire) s'accomplit. On aurait tort de croire qu'il est involontaire, automatique. Il est au contraire, tout à fait délibéré.
G. Duhamel, Inventaire de l'abîme, V.
♦ ☑ Loc. Écriture automatique. ⇒ Écriture (cit. 18 et supra). || Poème automatique : poème écrit par les procédés de l'écriture automatique.
1.1 Il s'agissait, en l'espèce, d'un poème automatique : tout de premier jet ou si peu s'en fallait qu'il pouvait passer pour tel en 1923, quand je lui donnai place dans Clair de Terre.
A. Breton, l'Amour fou, p. 79.
2 (1839). Cour. Qui, une fois mis en mouvement, fonctionne de lui-même; qui opère par des moyens mécaniques. || Appareil automatique. || Transporteur automatique. || Frein automatique. || Portillon (cit. 2) automatique, à fermeture automatique. || Boîte de vitesses automatique (opposé à mécanique), et, par ext., voiture automatique; conduite automatique (→ ci-dessous l'automatique, cit. 4). || Tourne-disque automatique, dont le bras s'abaisse et se relève automatiquement. || Commande automatique ou manuelle. || Montre automatique, que l'on n'a pas besoin de remonter à la main. || Répondeur automatique. || Distributeur automatique. — (1903, in Rev. gén. des sc., no 8, p. 411). || Téléphone automatique. — Signaux automatiques. || Arme automatique, dans laquelle la pression des gaz de combustion est utilisée pour réarmer. ⇒ Semi-automatique. || La mitrailleuse est une arme automatique. || Browning (cit. 2) automatique (→ ci-dessous, II.).
1.2 De nouveau c'est l'attaque, le bruit sec et saccadé des armes automatiques, plus ou moins proche derrière le petit bois (…)
A. Robbe-Grillet, Dans le labyrinthe, p. 160.
1.3 Si l'on remplaçait les garde-barrière par des appareils automatiques robustes et bien conçus, les accidents se résorberaient presque complètement. C'est la surveillance automatique qui, jointe aux machines-transfert, a rendu possible l'automatisation complète des usines (…)
A. David, la Cybernétique et l'Humain, 1965, p. 64, in T. L. F., art. Automatisme.
♦ Qui se fait sans intervention humaine, par des machines. || Traduction automatique. ⇒ Informatisé, programmé. || Documentation automatique (utilisant la mécanographie ou l'électronique). || Rendre un processus technique automatique. ⇒ Automatisation; automation.
3 (1878). Fig. Qui s'accomplit avec une régularité déterminée. || Une répression automatique, aveugle. || L'avancement automatique des fonctionnaires. || « Nous avons un système de relèvement automatique des salaires quand le coefficient du prix de la vie augmente » (Maurois). || Prélèvements automatiques sur un compte chèque.
2 Un mécanisme inséré dans la nature, une réglementation automatique de la société (…)
H. Bergson, le Rire, I, p. 36.
4 Fam. Qui doit forcément se produire. ⇒ Forcé, sûr. || Il va se ruiner, c'est automatique.
———
II N. m.
1 Pistolet automatique. ⇒ Browning. || Un automatique à la ceinture.
3 Gerfaut (…) sortit le Star de sa veste. Précipitamment et maladroitement, il ôta la sûreté de l'automatique.
— Haut les mains ! cria-t-il avec niaiserie.
J.-P. Manchette, Trois hommes à abattre, XI, p. 82.
2 Téléphone automatique, sans intervention de standardiste. || L'automatique, après avoir équipé les réseaux urbains, est progressivement étendu aux réseaux interurbains nationaux et à certaines liaisons internationales. || Le « cadran d'un automatique » (→ Téléphone, cit. 1.1).
4 Excusez-moi, dit Antoine, il faut que je téléphone.
Il courut jusqu'à chez lui, se disputa avec une dame des P. T. T. qui tardait à lui expliquer le fonctionnement de l'automatique dans le Var (…)
F. Sagan, la Chamade, p. 163.
———
III N. f.
1 Sc. Ensemble des disciplines scientifiques et des techniques utilisées pour la conception et l'emploi des dispositifs qui fonctionnent sans intervention d'un opérateur humain. ⇒ Automatisme, cybernétique, informatique. || Spécialiste de l'automatique. ⇒ Automaticien.
2 Montre automatique.
3 Utilisation du changement de vitesse automatique (dans une automobile).
5 En souplesse, le mastodonte décolla. Il n'y avait pas de changement de vitesse. — Ça vous plaît, l'automatique, mon capitaine ? Ça ne manque pas un peu de nerf ? — Tout dépend de la puissance du moteur.
Vladimir Volkoff, le Retournement, p. 312.
❖
CONTR. Conscient, délibéré, intentionnel, médité, prémédité, réfléchi, volontaire.
DÉR. Automaticien, automaticité, automatiquement, automatiser.
Encyclopédie Universelle. 2012.