AÉRODYNAMIQUE
L’aérodynamique, dont l’étymologie évoque immédiatement l’action de l’air en mouvement, est la science qui étudie les différents aspects de cette action, notamment les forces, pressions et moments qui résultent du déplacement des corps dans l’atmosphère. L’aérodynamique intervient essentiellement dans la conception des avions et des missiles, dont elle définit les formes optimales, mais joue également un rôle d’importance variable dans le dessin de bateaux, voitures rapides, véhicules à coussins d’air, ainsi que dans la construction d’ouvrages fixes comme les ponts, tours, ou grands immeubles, dont elle détermine les réactions au vent.
Sa naissance, comme science, peut être située au XVIIIe siècle, en Europe, où furent développées les théories (D. Bernoulli, 1738; L. Euler, 1755) qui faisaient suite à un empirisme séculaire.
Mais ce n’est qu’un siècle plus tard que les lois fondamentales tenant compte des contraintes intérieures d’un milieu continu ont été formulées (M. Navier, 1827; S. D. Poisson, 1831; D. de Saint-Venant, 1843; G. G. Stokes, 1845). Devant l’impossibilité de résoudre ces équations extrêmement compliquées, les connaissances aérodynamiques n’ont pu se développer que grâce à l’introduction d’hypothèses simplificatrices, appuyées sur l’expérience. Les étapes les plus importantes de ces travaux théoriques et expérimentaux sont marquées, entre autres, par l’introduction des coefficients de similitude (E. Mach, 1889; O. Reynolds, 1883), des notions de fluide parfait et de couche limite (L. Prandtl, 1904) dans le cas des écoulements à des vitesses modérées.
C’est également à la fin du XIXe siècle et au début du XXe que l’aérodynamique expérimentale a découvert les lois physiques, que les théoriciens ont eu à expliquer, concernant les phénomènes de la portance (N. I. Joukovski, 1904), de la traînée (W. Blasius, 1907), de la stabilité et du contrôle des avions subsoniques. L’accroissement de la vitesse, jusqu’à des valeurs supersoniques, a résulté des progrès de la technique, favorisés par le développement des connaissances aérodynamiques grâce d’abord aux balisticiens (Mach, 1887, P. H. Hugoniot, 1883). L’étude très difficile des écoulements transsoniques en est encore à un stade moins avancé, malgré les progrès intervenus récemment. La réalisation de missiles à très grande vitesse a provoqué de nouvelles recherches concernant les écoulements hypersoniques et l’effet des modifications physico-chimiques de l’air, liées aux températures élevées atteintes en vol.
1. Considérations théoriques
Mise en équations du problème et approximations
Mis à part quelques cas particuliers, comme celui de la très haute atmosphère, où les phénomènes dus à la raréfaction deviennent très importants, on peut considérer qu’un gaz est un milieu continu , dont le mouvement est décrit par les équations de Navier-Stokes (1 et 2).
La première traduit la conservation de la masse totale et la deuxième celle de la quantité de mouvement. Les notations utilisées sont classiques: 福 masse volumique, p pression, u i composante du vecteur vitesse u sur x i , f i , composante sur x i de l’accélération des forces de masse (pesanteur む ), 精 ik tenseur des contraintes (3), et 猪 sont les deux coefficients de viscosité du gaz, fonctions de la température.
À ces équations, il convient d’ajouter l’équation de l’énergie qui, en l’absence de réactions chimiques, s’écrit sous la forme (4). H = h + u 2/2 est l’enthalpie totale du fluide, somme de l’enthalpie massique h et de l’énergie cinétique massique u 2/2, tandis que q j désigne le flux de chaleur:
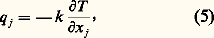
Ce système doit enfin être complété par la loi d’état du gaz qui, pour l’air, est très complexe; pratiquement, on est amené à considérer plusieurs lois distinctes selon les valeurs des vitesses, températures et pressions, et selon l’importance de leurs variations au cours du mouvement:
– Aux faibles vitesses (de 0 à 300 km/h), on peut en général considérer l’air comme un fluide homogène et incompressible, pour lequel:
– Aux vitesses moyennes (de 300 à 2 000 km/h), les effets de la compressibilité deviennent importants, et l’air se comporte sensiblement comme un gaz parfait pour lequel:
– Enfin, aux très grandes vitesses, l’air s’écarte de plus en plus du gaz parfait. Ces effets dits de gaz réel , qui se traduisent en particulier par l’apparition de réactions chimiques et d’ionisation, seront étudiés dans le paragraphe «domaine hypersonique».
À ces équations, on doit ajouter les conditions aux limites suivantes:
– Écoulement donné à l’infini, en général uniforme.
– Vitesse nulle sur le corps traduisant l’hypothèse de l’adhérence du fluide à la paroi.
Le problème ainsi posé doit permettre d’accéder aux champs des vitesses, pressions, frottements, températures, etc. dans tout le fluide; en fait, d’un point de vue pratique, on cherche à déterminer ces grandeurs sur la paroi en vue d’en déduire notamment la trainée F x et la portance F z de l’obstacle, qui sont respectivement les composantes de la résultante aérodynamique づ, dans la direction de la vitesse ぴ 秊 à l’infini et dans le plan perpendiculaire à ぴ 秊 (fig. 1). D’autres grandeurs importantes sur le plan pratique sont les flux de chaleur en tout point de la paroi et sa température locale. Toutes ces grandeurs, comme pour d’autres disciplines de la physique, sont réduites en coefficients sans dimension . On définit ainsi les coefficients de traînée et de portance par les formules:
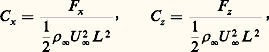
où 福 size=1秊 et U size=1秊 désignent respectivement la masse volumique et le module de la vitesse à l’infini amont, L 2 = S étant une surface caractéristique du corps (telle que la surface de l’aile pour un avion).
On définit de façon analogue divers coefficients de moment ainsi que des coefficients locaux tels que ceux de flux de chaleur, de pression K p et de frottement C f:
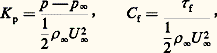
où 精 f est la tension de frottement du fluide sur la paroi.
La détermination de ces quantités est un problème mathématique très complexe, essentiellement par suite de la non-linéarité des équations du mouvement (1) à (4), dont on ne connaît que très peu de solutions analytiques exactes. Pratiquement, on est donc amené soit à utiliser des méthodes numériques souvent coûteuses (cf. chap. 3), soit à rechercher, par voie théorique, des solutions approchées: c’est ce que nous allons examiner ci-dessous.
Première simplification: paramètres de similitude
Lorsqu’on écrit les équations sous forme adimensionnelle en choisissant pour grandeurs de référence les conditions à l’infini, on voit apparaître plusieurs nombres sans dimension et on peut simplifier le problème si ces paramètres ont des valeurs très grandes ou très petites. Les principaux parmi ces paramètres de similitude sont:
– le nombre de Reynolds Re = ( 福 size=1秊U size=1秊L )/ 猪 size=1秊,
Dans les applications industrielles, notamment en aéronautique, le nombre de Reynolds Re est souvent très grand, si bien que les effets dus à la viscosité sont négligeables en première approximation: c’est ce que l’on nomme l’approximation de fluide parfait. En fait, cela reste vrai partout où il n’existe pas de gradients de vitesse trop importants; c’est le cas dans la majeure partie de l’écoulement, sauf au voisinage des parois ou dans les problèmes de mélange de jets, où la viscosité devient essentielle; c’est elle qui donne lieu en particulier au phénomène de couche limite étudié ci-après.
Le nombre de Froude est, lui aussi, très grand, si bien que, sauf dans des cas très particuliers comme l’étude des phénomènes météorologiques ou l’aérodynamique des ballons et dirigeables, les forces de pesanteur sont négligeables.
Le nombre de Mach joue un rôle très important:
– s’il est petit (inférieur à 0,3 pour fixer les idées), on peut considérer que le fluide est incompressible ;
– s’il est inférieur à 1, on dit que l’on est dans le domaine subsonique , et les équations du mouvement de fluide parfait sont elliptiques;
– s’il est voisin de 1, c’est le domaine transsonique , de type mixte, très difficile à étudier;
– s’il est plus grand que 1, on se trouve dans le domaine supersonique , caractérisé par des équations hyperboliques et par l’apparition d’ondes de choc ;
– enfin, s’il est très grand devant 1, on se trouve dans le domaine hypersonique où de nouvelles approximations sont possibles, mais où l’apparition de réactions chimiques vient compliquer le problème.
Seconde simplification: petites perturbations
Un second type de simplification est dû au fait que, bien souvent, les corps que l’on considère perturbent peu l’écoulement: c’est le cas en particulier de l’aile mince ou du corps élancé. Il s’ensuit que l’on peut fréquemment linéariser l’écoulement autour d’un écoulement connu, et obtenir ainsi une excellente approximation des effets cherchés.
Méthode générale d’étude et limitation
Pratiquement, on cherche à construire une solution stationnaire , en commençant par négliger complètement les effets de la viscosité. Cette étude, en fluide parfait, permet de définir une première approximation du coefficient de portance C z et du coefficient de traînée C x . Celui-ci apparaît ainsi comme la somme d’une «traînée induite» due à la portance, et, en écoulement supersonique, d’une «traînée d’onde».
On corrige ensuite l’écoulement obtenu en tenant compte de la viscosité, ce qui conduit, en particulier, à la très importante théorie de la couche limite, qui permet le calcul de la traînée de frottement, et du flux de chaleur à la paroi.
On voit en quoi cette méthode est critiquable: en effet, rien ne prouve que la solution ainsi définie soit stable dans le temps, et, effectivement, elle ne l’est pas toujours; si tel est le cas, il y a deux possibilités:
– ou bien il existe une autre solution, stationnaire, stable, au même problème; c’est ce qui se produit, par exemple, s’il y a décollement de l’écoulement, c’est-à-dire lorsque les filets fluides provenant de l’infini amont contournent l’obstacle sans rester au contact de toute sa surface; l’étude du décollement est difficile et encore très incomplète, mais il existe des méthodes plus ou moins justifiées pour prévoir son apparition, en particulier grâce à la théorie de la couche limite;
– ou bien il n’existe pas de solution stationnaire stable au problème: l’écoulement est alors complètement instationnaire, comme le montre la figure 2 représentant les tourbillons de Karman en aval d’un bord de fuite cylindrique: de tels écoulements instationnaires sont à éviter au maximum dans le cas des avions ou des missiles, car ils entraînent en général des efforts importants et rapidement variables sur les structures; celles-ci n’étant jamais parfaitement rigides, il peut alors se produire un couplage entre leurs déformations et l’écoulement externe; c’est là l’origine du très grave phénomène de flottement aéroélastique.
Ces problèmes, très complexes, donnent lieu à l’heure actuelle à de nombreuses études, dont les plus prometteuses sont probablement les théories non linéaires de la stabilité.
Mouvements stationnaires d’un fluide parfait
Si on néglige complètement la viscosité (Re = 秊), les équations de Navier-Stokes se simplifient considérablement pour donner les équations d’Euler caractérisant tous les mouvements de fluide parfait. Dans ce cas, on établit un certain nombre de propriétés mathématiques de ces équations dites «théorèmes généraux » (cf. Mécanique des FLUIDES), qui permettent d’affirmer, sous réserve qu’il n’y ait pas d’irréversibilités telles que des chocs dans l’écoulement, que celui-ci est irrotationnel et qu’il existe, par suite, un potentiel des vitesses 﨏 tel que:
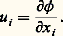
Ce potentiel vérifie l’équation de Steichen:
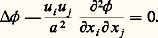
Domaine incompressible
Pour de faibles nombres de Mach, on a vu que l’air pouvait être considéré comme incompressible. Il en résulte que l’équation de Steichen se réduit à l’équation de Laplace:
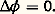
On aboutit donc à une équation linéaire bien connue, pour laquelle on dispose de méthodes mathématiques de résolution classiques, même pour un corps de forme arbitraire. Parmi ces méthodes, on peut citer celle basée sur la théorie des distributions, qui permet de déterminer le potentiel 﨏 par superposition de solutions élémentaires, qui sont des sources ou tourbillons généralement distribués de façon convenable sur la surface limitant l’obstacle ou à l’intérieur même de celui-ci. Le potentiel 﨏 , donc les vitesses, étant déterminé, on obtient ensuite le champ des pressions et, par conséquent, les efforts sur le corps par l’intégrale de Bernoulli:
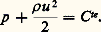
Dans le cas des écoulements bidimensionnels, on peut utiliser une méthode basée sur la considération du potentiel complexe f défini par:
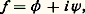
où 祥 désigne la fonction de courant:
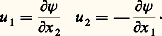
Partant d’un écoulement connu exactement, tel que l’écoulement autour d’un cercle, on effectue alors des transformations conformes , qui ont pour effet de transformer le cercle en un autre corps et de fournir ainsi la solution exacte de l’écoulement autour de ce nouveau corps. Cette méthode permet en particulier de définir et d’étudier un très grand nombre de profils d’ailes, tels que les profils Joukovski ou Karman-Trefftz, pour lesquels toutes les propriétés aérodynamiques peuvent être obtenues sous forme analytique exacte.
Une autre méthode extrêmement intéressante est l’utilisation de l’analogie électrique , décrite plus loin, et qui utilise le fait que le potentiel électrique vérifie également l’équation de Laplace: par de simples mesures de potentiel, on est ainsi capable de définir tout le champ de l’écoulement.
Remarquons cependant qu’on se heurte à une importante difficulté dans la résolution de l’équation de Laplace avec les conditions limites imposées, car il n’y a pas unicité de la solution: pour lever cette indétermination, on est conduit à appliquer la «condition de Joukovski», qui impose de conserver des vitesses finies au bord de fuite du profil, ce qui revient à dire que la ligne de séparation entre les écoulements intrados et extrados est issue du bord de fuite. Cette condition impose ainsi une circulation 臨 de la vitesse, autour du profil, non nulle, et la portance est directement proportionnelle à cette circulation en vertu du théorème de d’Alembert. Cependant, dans le cadre de la théorie du fluide parfait, il est impossible d’expliquer la provenance de cette circulation et c’est, en fait, la viscosité, aussi faible soit-elle, qui permet l’établissement de la circulation nécessaire à la portance.
L’utilisation de la méthode des petites perturbations permet d’autre part de traiter de façon approchée, mais très simple, les écoulements autour des profils minces et des corps élancés de forme arbitraire et d’aboutir là aussi à des formules analytiques.
De toutes ces méthodes, il ressort que l’on est capable d’évaluer le coefficient de pression locale sur le corps, d’où le coefficient de portance C z qui, en première approximation, est proportionnel à l’incidence; on aboutit toujours à un coefficient de traînée C x nul, ce qui est conforme au «paradoxe de d’Alembert», mais physiquement inadmissible.
Cette difficulté se trouve levée dans la théorie tridimensionnelle de la ligne portante, ou théorie de Prandtl, basée sur le fait que l’écoulement n’est pas partout irrotationnel: il existe un sillage tourbillonnaire que l’on peut assimiler, en première approximation, à une surface de discontinuité de vitesse et qui s’étend depuis l’aile jusqu’à l’infini aval; cette théorie, qui fait appel à la présence de tourbillons, a eu un très gros succès, car elle a permis d’expliquer la présence d’une traînée induite par la portance et donnée par la formule:
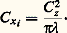
Il apparaît ainsi que la traînée induite est inversement proportionnelle à l’allongement de l’aile, que l’on a donc intérêt à augmenter, et que la polaire de l’aile, c’est-à-dire la courbe C x = f (C z ), est une parabole, ce qui est assez bien confirmé expérimentalement lorsqu’on néglige les effets de la viscosité.
Domaine compressible subsonique
Dans le cas général d’un écoulement irrotationnel, le mouvement est décrit par l’équation de Steichen complète, quasi linéaire, de type elliptique pour un nombre de Mach inférieur à l’unité. En dehors des résolutions purement numériques, quelques résultats peuvent être obtenus par la méthode de l’hodographe qui consiste à raisonner dans l’espace des vitesses, mais le retour au plan physique soulève souvent des difficultés. En revanche, les méthodes de petites perturbations sont très intéressantes: c’est ainsi que, par linéarisation de l’équation de Steichen, on peut montrer que l’écoulement compressible autour d’un profil mince se déduit immédiatement de la connaissance de l’écoulement incompressible par l’affinité de Prandtl-Glauert. Le résultat, très simple,
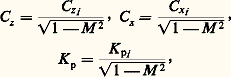
où l’indice i indique les valeurs incompressibles, n’est toutefois valable que si le nombre de Mach reste assez éloigné de l’unité.
Domaine supersonique
L’étude des écoulements supersoniques est relativement plus facile, malgré l’apparition de phénomènes nouveaux, tels que les ondes de choc.
Cette relative facilité est due au fait qu’une petite perturbation en un point d’un écoulement supersonique ne se fait pas sentir dans tout l’espace, mais seulement, à l’aval de ce point, dans un domaine limité, en écoulement bidimensionnel, par deux courbes dites caractéristiques , qui s’identifient physiquement avec les lignes de Mach. La théorie mathématique des caractéristiques, fondée sur le fait que les équations du mouvement sont de caractère hyperbolique, est très développée et bien au point. Elle permet, entre autre, le calcul numérique des écoulements, par des méthodes de différences finies.
Le deuxième caractère des écoulements supersoniques est l’apparition possible d’ondes de choc qui, en fluide parfait, se réduisent à des surfaces de discontinuité des grandeurs physiques. Ces discontinuités sont connues depuis fort longtemps, puisque la première étude en a été faite par Riemann dès 1860, puis par Rankine et Hugoniot, qui ont établi les formules donnant les valeurs des discontinuités à la traversée de l’onde de choc droite, c’est-à-dire normale à l’écoulement. On constate que l’onde de choc est un phénomène irréversible, entraînant un ralentissement de l’écoulement et accompagné d’une augmentation de la pression de la masse volumique et de la température. Si M 1 est le nombre de Mach amont, on montre en particulier que:
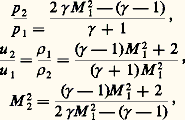
塚 désignant le rapport C p/C v des chaleurs massiques à pression et volume constants ( 塚 = 1,4 environ pour l’air).
Ces formules ont été généralisées ensuite à l’onde de choc oblique , accompagnée d’une déviation brusque de l’écoulement et étudiée par Busemann dans le cas de l’écoulement sur un dièdre.
La polaire de choc de Busemann, qui est dans le plan de l’hodographe le lieu de l’extrémité du vecteur vitesse en aval du choc lorsque l’angle du dièdre varie, montre en particulier qu’il existe une déviation limite au-delà de laquelle le choc se détache du sommet du dièdre. On constate bien expérimentalement l’existence de ces chocs détachés non rectilignes, à l’aval desquels l’écoulement cesse d’être uniforme et, surtout, n’est plus irrotationnel. L’apparition d’un tourbillon derrière les chocs non rectilignes est directement liée à la variation d’entropie à travers les chocs, c’est-à-dire finalement à l’irréversibilité du mouvement. La détermination de la position et de l’intensité des chocs détachés est un problème mathématique extrêmement complexe qui, dans la pratique, n’est guère abordé que par intégration numérique des équations du mouvement, ou par étude expérimentale.
Dans le cas simple où le corps ne perturbe que peu l’écoulement et où le choc reste attaché au nez de l’obstacle, on est capable de généraliser la méthode des petites perturbations en conservant la notion de potentiel des vitesses, tout au moins en première approximation, car l’irrotationnalité du mouvement ne tombe en défaut qu’à un ordre d’approximation supérieur.
Le potentiel de perturbation 﨏 vérifie alors une équation linéaire hyperbolique du type:
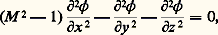
qui admet pour solution élémentaire la «source supersonique»:
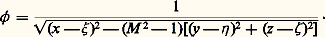
En écoulement bidimensionnel, on peut ainsi, par superposition de «sources supersoniques», obtenir les formules dites d’Ackeret donnant la portance et la traînée d’un profil de longueur L , placé à l’incidence i , et dont la forme est définie par les équations de l’extrados y = f +(x ) et de l’intrados y = f -(x ):
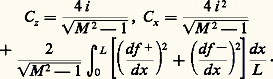
Donc, même pour un écoulement irrotationnel, et même à incidence nulle, il apparaît, contrairement au cas subsonique, une traînée dite traînée d’onde directement liée à la forme du profil.
Il est également possible, toujours par superposition de «sources supersoniques», de traiter numériquement, sinon analytiquement, des problèmes tridimensionnels stationnaires et instationnaires.
Domaine transsonique
Du point de vue théorique, l’étude des phénomènes qui interviennent pour un nombre de Mach voisin de l’unité est très complexe. Les difficultés essentielles proviennent à la fois du changement de type de l’équation qui est elliptique dans les zones subsoniques et hyperbolique dans les zones supersoniques, et de la non-linéarité fondamentale des phénomènes, même si on se limite à l’étude de petites perturbations. On est ainsi conduit soit à faire des études expérimentales, soit à raisonner sur des équations de type mixte, représentant des écoulements de fluide fictif, telles que l’équation de Tricomi.
Pratiquement, le calcul direct de l’écoulement transsonique autour d’un profil mince bidimensionnel et, a fortiori, autour d’une surface portante tridimensionnelle, demeure un problème très difficile, même par voie numérique.
Domaine hypersonique
Le domaine hypersonique est un cas particulier des écoulements supersoniques, assez mal défini en ce sens qu’il n’existe pas de limite inférieure précise pour définir le régime hypersonique.
Pratiquement, on considère que le nombre de Mach doit être supérieur à 7.
C’est cependant un cas théorique limite important, car l’inverse du nombre de Mach joue alors dans les équations le rôle d’un petit paramètre permettant la construction d’un nouveau type de développement asymptotique: c’est sur ce fait qu’est basée la théorie hypersonique des petites perturbations , très fructueuse, dont les deux résultats les plus importants sont la notion d’analogie du piston (ou analogie de l’explosion), due à C. Hayes, et la notion de similitude hypersonique .
L’analogie du piston consiste à affirmer que tout écoulement hypersonique, stationnaire ou non, sur une aile mince ou un obstacle élancé est équivalent à un écoulement instationnaire à une dimension de moins; l’analogie en question est précisée sur la figure 3: il faut imaginer que la fente FF de la figure est immobile alors que les axes Oxy sont entraînés vers la gauche avec la vitesse U size=1秊 de l’obstacle. Un observateur lié à la fente voit alors l’écoulement transversal, instationnaire, qui lui apparaît comme étant provoqué par le déplacement brusque d’un piston.
La notion de similitude hypersonique est fort précieuse car elle permet d’exploiter les résultats expérimentaux. En ce qui concerne les efforts globaux sur une aile mince, elle s’exprime sous la forme:
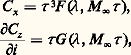
où désigne l’allongement de l’aile et 精 = e /L son épaisseur relative: on voit que l’on peut ainsi évaluer les efforts sur une aile donnée lorsqu’on les connaît sur une autre aile, à condition que soient vérifiées les «conditions de similitude»: même allongement et même valeur pour le produit M size=1秊 精 .
Une autre théorie hypersonique importante et déjà ancienne, est la «théorie de Newton», qui n’assimile pas le gaz à un milieu continu et n’utilise donc pas les équations de Navier-Stokes: l’hypothèse fondamentale revient à admettre qu’aux vitesses hypersoniques, les particules constituant le gaz viennent frapper le corps sans subir aucune déviation préalable, et repartent tangentiellement à la paroi, créant autour de celle-ci une couche de très forte densité et d’épaisseur négligeable.
Cette théorie élémentaire est d’autant plus valable que le nombre de Mach est plus élevé; elle fournit des résultats simples, tels que l’expression du coefficient de pression en un point où le plan tangent à l’obstacle fait l’angle avec la vitesse à l’infini:
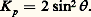
Revenant à une description continue de l’écoulement, on ne peut passer sous silence l’importance considérable des effets de gaz réels aux vitesses hypersoniques: les températures atteintes en aval des ondes de choc sont telles qu’il se produit à la fois dissociation et ionisation de l’air. Les principales réactions sont les suivantes:
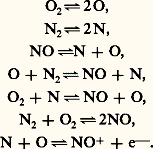
Une étude théorique montre que le champ des pressions n’est pas sensiblement affecté par ces effets de gaz réels, mais que le champ des températures est, lui, considérablement influencé. Ces effets sont particulièrement importants dans la couche limite, où ils seront repris, et sont calculables numériquement au moyen de puissants ordinateurs. À titre d’exemple, pour un mobile entrant dans l’atmosphère à une vitesse de 4 km/s, l’air est porté à une température de 5 000 K environ, alors que, sans effet de gaz réel, cette température serait de 8 000 K.
Le degré d’ionisation est de l’ordre de 10-5; il reste faible, mais suffit cependant à perturber les liaisons radio avec un missile en cours de rentrée, au point de les supprimer complètement.
2. Viscosité: concept de couche limite
Écoulement d’un fluide faiblement visqueux
La viscosité d’un fluide, qui n’est jamais strictement nulle, peut modifier considérablement l’écoulement que la théorie du fluide parfait avait laissé prévoir.
La viscosité est responsable de phénomènes aussi importants que le frottement à la paroi, l’échauffement cinétique, le décollement, la création de la circulation nécessaire à la sustentation, etc. Elle joue, par ailleurs, un rôle très important dans l’étude des sillages.
En aérodynamique, on se limite à l’étude des fluides faiblement visqueux dont les mouvements sont caractérisés par des nombres de Reynolds très grands, le cas des faibles nombres de Reynolds relevant plutôt de la mécanique des fluides.
Outre la viscosité, les fluides réels possèdent aussi des propriétés de conductibilité thermique et de diffusion massique. À l’échelle macroscopique, ces propriétés se traduisent par des effets de diffusion de quantité de mouvement, de diffusion de chaleur et de masse qui apparaissent dans les écoulements lorsque ceux-ci présentent des non-uniformités importantes de vitesse, de température, de pression ou de concentration des espèces chimiques constituant le gaz. En aérodynamique, ces phénomènes se concentrent essentiellement au voisinage des parois où se forme la couche limite, dans les sillages qui résultent de la confluence de couches limites ou encore dans les jets. La viscosité, la conductibilité thermique et la diffusion massique sont des propriétés du fluide qui ont une interprétation à l’échelle moléculaire dans le cas des gaz. À l’aide de la théorie cinétique, on montre que ces propriétés résultent du bilan statistique des échanges de quantité de mouvement et d’énergie lors des chocs moléculaires. Ces propriétés peuvent se calculer théoriquement si l’on connaît les lois d’interaction entre les molécules.
Équations de la couche limite
Couche limite laminaire
Dans un écoulement, le nombre de Reynolds caractérise le rapport des forces d’inertie aux forces de viscosité. Or, en aérodynamique, ce nombre est très grand devant l’unité. On pourrait en conclure que les forces de viscosité sont négligeables. C’est vrai presque partout mais il existe des régions, comme la couche limite, où les effets visqueux restent significatifs. De fait, la couche limite est définie comme étant le lieu où les effets visqueux sont du même ordre que les effets d’inertie. Alors, une analyse d’ordre de grandeur montre que l’épaisseur 嗀 de la couche limite est d’ordre L / 連Re , où L représente la longueur de développement de la couche limite, et Re le nombre de Reynolds associé. Grâce à cette hypothèse introduite par Prandtl, les équations de Navier-Stokes se simplifient. Soit par analyse d’ordre de grandeur des termes des équations de Navier-Stokes, soit par la technique des développements asymptotiques raccordés, on aboutit au système d’équations (7, 8, 9) valables en bidimensionnel.
Ici x est l’abscisse curviligne le long de la paroi sur laquelle se développe la couche limite, et y est la coordonnée normale à la paroi. Les composantes de la vitesse suivant x et y sont u et v . Avec l’hypothèse de couche limite, l’enthalpie d’arrêt H est liée à l’enthalpie h par H = h + u 2/2.
Il est à noter que l’hypothèse de l’aérodynamique (Re 拾 1) conduit en fait à une double approximation. Près de la paroi, c’est le domaine de la couche limite, et au-delà, c’est le domaine du fluide parfait, où les effets visqueux sont négligeables en première approximation.
Le système (7) à (9) est à compléter par l’équation d’état et les conditions initiales et aux limites imposant l’adhérence du fluide à la paroi et assurant le raccord avec l’écoulement extérieur.
L’équation (8b) montre que la pression est constante sur une normale à la paroi. En conséquence, la pression mesurée à la paroi est égale à la pression qui règne à la frontière de la couche limite. Pour calculer la couche limite autour d’un corps donné, on procède en deux étapes successives:
– Les équations relatives au fluide parfait sont résolues d’abord. Il en résulte notamment l’état d’écoulement à la paroi y = 0.
– Le calcul de la couche limite est effectué ensuite. Les répartitions pariétales précédemment trouvées sont imposées à la couche limite par l’intermédiaire des termes 煉p / 煉t et 煉p / 煉x et des conditions aux limites en y秊.
Couche limite turbulente
Dans la plupart des cas pratiques, l’écoulement n’est pas partout laminaire. Après une phase dite de transition, il devient turbulent. Une véritable théorie de la turbulence n’existe pas et constitue l’un des défis de la physique moderne. Pour déterminer les effets de la turbulence, des techniques sont mises en jeu dans lesquelles des informations expérimentales sont introduites. Ces informations sont aussi extraites des méthodes de simulation de la turbulence: il s’agit de solutions numériques aux équations de NavierStokes instationnaires. La difficulté majeure soulevée par ces résolutions provient de ce que les fluctuations turbulentes de l’écoulement couvrent une gamme d’échelles très large et d’autant plus large que le nombre de Reynolds est élevé. Le cisaillement induit dans l’écoulement par les différences de vitesse qui y règnent est à l’origine de la formation de structures turbulentes dont la dimension (l’échelle de longueur) est de l’ordre de grandeur de l’épaisseur de la couche cisaillée. Le nombre de Reynolds caractéristique de ces structures est très grand devant l’unité, de sorte que les effets visqueux sont faibles à leur échelle. Par des mécanismes non linéaires, ces structures donnent naissance à une cascade de structures de plus en plus fines. La taille des plus fines est telle que le nombre de Reynolds qui les caractérise est de l’ordre de l’unité, de sorte que le travail des tensions visqueuses associées transforme entièrement leur énergie cinétique en chaleur; c’est le phénomène de dissipation, dont le rôle est essentiel dans l’étude des écoulements turbulents. Le rapport des échelles de longueur entre les plus grosses et les plus petites structures augmente comme la puissance 3/4 du nombre de Reynolds des grosses structures. On conçoit alors qu’il est difficile numériquement de calculer toutes les échelles de l’écoulement, car la taille de mémoire ordinateur nécessaire devient vite extraordinairement élevée. Pour contourner cette difficulté, des méthodes de simulation des grosses structures ont été élaborées. Elles consistent à filtrer l’écoulement et les équations qui le régissent. Les grosses structures sont alors calculées par ces équations filtrées dans lesquelles l’influence des petites structures est représentée par un modèle appelé modèle de sous-maille. Ces méthodes permettent d’étudier des écoulements à plus grand nombre de Reynolds que les méthodes de simulation directe.
Pour les applications pratiques de l’ingénieur, une approche plus radicale encore est utilisée. Elle consiste à séparer l’écoulement en une composante moyenne (au sens statistique) et une composante fluctuante. On a ainsi par exemple:
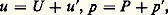
où u et p sont les valeurs instantanées de la vitesse suivant x et de la pression, U et P sont les valeurs moyennes, u et p sont les fluctuations dont la moyenne est nulle.
Avec les simplifications dues aux hypothèses de couche limite, pour un écoulement bidimensionnel en moyenne, on obtient les équations (10, 11, 12).
En écoulement compressible, l’établissement des équations est en principe plus compliqué. On fait généralement appel aux moyennes de Favre (moyennes pondérées par la masse), et les équations contiennent quelques termes supplémentaires. Cependant, jusqu’à des nombres de Mach de l’ordre de 5 on peut raisonner de façon pratiquement équivalente sur les moyennes statistiques et on aboutit aux équations (10, 11, 12).
Dans ces équations, l’effet de la turbulence se traduit par la corrélation 漣 福 麗u v 礪, qui apparaît comme une tension turbulente apparente, appelée tension de Reynolds; il se traduit aussi par la corrélation 福 麗v h 礪 entre la fluctuation de vitesse v et la fluctuation d’enthalpie h , qui apparaît comme un flux de chaleur turbulent apparent. Ces corrélations sont des inconnues supplémentaires des équations (10, 11, 12). Elles doivent être exprimées à l’aide d’un modèle (modèle de turbulence) pour que les équations (10, 11, 12) puissent être résolues. Le problème de la modélisation de la turbulence est encore loin d’être résolu et fait l’objet de recherches poussées. Sa solution est l’une des clés de l’aérodynamique numérique.
Physiquement, la turbulence se traduit par un mélange accru de l’écoulement qui met au contact des régions relativement éloignées les unes des autres et possédant des vitesses et des températures très différentes. L’effet de mélange a tendance à gommer ces différences de vitesse et de température. Il en résulte que les coefficients d’échange aux parois sont plus élevés; c’est le principe des échangeurs de chaleur. Le coefficient de frottement pariétal est donc considérablement augmenté ainsi que le coefficient de flux de chaleur pariétal (fig. 4). Une autre conséquence fondamentale est que la tendance au décollement est très réduite en régime turbulent (cf. infra ).
Équations globales
Des analyses simplifiées reposent sur des bilans globaux (de masse, de quantité de mouvement, d’énergie, etc.) dans l’épaisseur de la couche limite. Par exemple, l’équation globale de quantité de mouvement est obtenue en intégrant l’équation (11a ) par rapport à y entre y = 0 et y秊. En stationnaire, elle s’écrit:
où 精 p représente la contrainte de frottement pariétale. L’épaisseur 嗀 1 caractérise l’effet de déplacement de l’écoulement extérieur dû à la présence de la couche limite, et représente la perte de quantité de mouvement dans la couche limite. L’indice «e» désigne l’état à la frontière de la couche limite.
Les méthodes intégrales consistent à calculer la couche limite en résolvant les équations globales auxquelles sont jointes des lois entre les caractéristiques globales de la couche limite.
Couches limites laminaires stationnaires bidimensionnelles
Couches limites incompressibles
Lorsqu’un gaz est traité comme un fluide incompressible, non seulement sa masse volumique 福 mais aussi ses coefficients de viscosité 猪 et de conduction thermique ainsi que sa chaleur massique c sont constants. Le problème dynamique (équations de continuité et de quantité de mouvement) peut alors être résolu indépendamment du problème thermique (équation de l’énergie).
Des solutions particulières à ces équations existent lorsque la vitesse à la frontière de la couche limite est de la forme u e = C te . x m .
Des considérations de similitude suggèrent l’introduction des variables indépendantes:
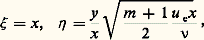
et de la variable dépendante:
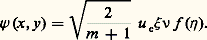
L’équation de quantité de mouvement devient:
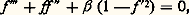
avec:
L’équation ainsi obtenue (équation de Falkner-Skan) est résolue avec les conditions aux limites:
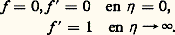
Physiquement, cette situation représente la couche limite sur un dièdre semi-infini d’angle d’ouverture 廓 神.
La figure 5 reproduit les solutions de l’équation de Falkner-Skan et montre que le profil de vitesse f = u /u e dépend de 廓 , paramètre de gradient de pression. Le cas 廓 礪 0 [(dp /dx) 麗 0] représente un écoulement extérieur accéléré. Le cas particulier 廓 = 0 [(dp /dx ) = 0] correspond à la couche limite sur une plaque plane, problème qui a été examiné par Blasius. On notera l’apparition d’un point d’inflexion dans le cas des écoulements ralentis caractérisés par 廓 麗 0 [(dp /dx) 礪 0]. Les profils de vitesse dotés d’un point d’inflexion dénotent une instabilité vis-à-vis de petites perturbations; il faut donc s’attendre à la destruction de l’état laminaire lorsque la couche limite est soumise à un gradient de pression positif. Pour 漣 0,1988 麗 廓 麗 0, Stewartson a montré l’existence d’une solution double; pour l’une d’entre elles, la vitesse u est partout positive dans l’épaisseur de la couche limite, alors que pour l’autre, il existe une zone à contre-courant (u 麗 0) près de la paroi. La limite 廓 = 漣 0,1988 correspond à une pente à l’origine nulle du profil de vitesse ce qui, en écoulement bidimensionnel, caractérise le décollement.
En pratique, la vitesse à la frontière extérieure n’est pas dans le cas général de la forme u e = C te . x m et la séparation des variables n’est pas possible. Néanmoins, les «solutions semblables» sont d’une importance capitale pour la compréhension des phénomènes. En particulier, la tendance de la couche limite à devenir instable ou à décoller sous l’effet d’un gradient de pression positif est clairement mise en évidence.
Le décollement s’explique par la perte d’énergie cinétique des particules fluides les plus voisines de la paroi, freinées à la fois par l’action du frottement et par le gradient de pression adverse (positif); elles s’immobilisent donc en un certain point au-delà duquel l’écoulement est dirigé en sens inverse. Pour assurer la continuité de débit, la couche limite est contrainte de quitter la paroi, devenant ainsi une couche de mélange. Cette situation est schématiquement représentée sur la figure 6. Selon la configuration géométrique de l’écoulement, la couche limite peut recoller sur la paroi. La figure 7 en donne un exemple choisi dans le domaine hypersonique. Le «fluide mort» enfermé entre le corps et la couche limite décollée n’est pas au repos, il est entraîné par la couche visqueuse et circule le long de trajectoires fermées sur elles-mêmes.
La répartition de pression à la paroi dans une région décollée diffère totalement de la répartition calculée en fluide parfait. C’est notamment ce qui se produit sur une aile, lorsque, l’incidence croissant, un décollement se forme sur l’extrados; il en résulte un large sillage qui diminue la sustentation et qui donne naissance à une traînée de pression.
Couches limites compressibles
Tout ce qui a été dit à propos des couches limites incompressibles reste qualitativement valable lorsque les effets de la compressibilité interviennent dans le domaine des nombres de Mach subsoniques élevés ou supersoniques.
Outre les nombres de Reynolds et de Mach, un paramètre particulièrement intéressant est le nombre de Prandtl Pr = ( 猪 / 福 )/( / 福 C p ), rapport de la viscosité cinématique à la diffusivité thermique. Lorsque Pr = 1, le taux d’échange de quantité de mouvement par diffusion entre filets fluides est égal au taux d’échange de chaleur. Cette égalité se traduit par la disparition du terme:
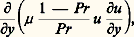
dans l’équation de l’énergie qui admet alors deux intégrales particulières:
– l’intégrale de Buseman:
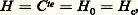
qui s’applique lorsque la paroi est thermiquement isolée;
– l’intégrale de Crocco:
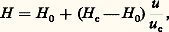
Ces intégrales jouent un rôle important dans la théorie des couches limites compressibles car, le nombre de Prandtl étant assez proche de l’unité (pour l’air, Pr = 0,725), l’hypothèse Pr = 1 constitue souvent une approximation raisonnable pour les problèmes réels.
Le freinage non uniforme des filets fluides sous l’action de la viscosité transforme l’énergie cinétique en chaleur et crée un champ de température non uniforme donnant lieu à des flux de chaleur au sein de la couche limite. Lorsque la paroi est thermiquement isolée, une solution particulière de l’équation d’énergie avec Pr = 1 est H = C te : l’enthalpie d’arrêt se conserve comme en fluide non visqueux; dans ces conditions le travail (extérieur) des forces visqueuses est exactement compensé par le transport diffusif de chaleur. Lorsque Pr 麗 1, la chaleur s’écoule plus facilement, et la température T f de la paroi thermiquement isolée diminue. Il est d’usage de caractériser ce phénomène par le facteur thermique pariétal r = (H f 漣 h e)/(H e 漣 h e) de l’énergie cinétique disponible H e 漣 h e, seule la fraction H f 漣 h e se traduit par une augmentation de température de paroi. Des résultats numériques montrent qu’avec une bonne approximation on a r = 連Pr . Lorsque la paroi n’est pas isolée, le flux de chaleur reçu par la paroi (H 0 麗 H f) ou cédé par la paroi (H 0 礪 H f) est proportionnel à la différence H 0 漣 H f et non à H 0 漣 h e.
D’après ce qui précède, l’existence de la couche limite entraîne deux conséquences importantes dans le domaine compressible:
– lorsque H e est très élevé (vol hypersonique), H f l’est aussi, et les parois doivent être refroidies énergiquement ou protégées par un «bouclier thermique» pour maintenir leur température à un niveau compatible avec leur résistance mécanique;
– il est impossible de mesurer la température d’un écoulement en y plaçant un thermomètre, celui-ci indiquerait une température voisine de T f en raison de sa propre couche limite.
Couches limites hypersoniques
Dans le domaine hypersonique, une première catégorie de phénomènes nouveaux est liée à l’augmentation considérable de l’épaisseur de la couche limite avec le nombre de Mach. On démontre que ( 嗀 /L ) 黎 (M 2/ 連Re L ). Le déplacement que subit l’écoulement extérieur peut donner lieu à une répartition de pression p (x ) notablement différente de celle que l’on calculerait en fluide parfait autour du corps géométrique.
Les hautes énergies mises en jeu en vol hypersonique donnent lieu à une autre catégorie de phénomènes, de nature physico-chimique. Dans l’équation d’énergie généralisée, il est tenu compte des chaleurs de dissociation libérées par les réactions chimiques et diffusées à travers la couche limite. Les concentrations massiques c i = 福 i / 福 des n espèces chimiques différentes sont déterminées par n équations de conservation:
Le terme 陸i représente le flux de diffusion massique. Il est exprimé par un modèle que la théorie cinétique des gaz permet de préciser.
Le taux de production chimique 諸i de l’espèce i résulte de la création (ou de la destruction) de cette espèce dans les diverses réactions chimiques en présence. Ce terme est souvent mal connu à cause de l’imprécision qui règne sur la connaissance des vitesses de réaction.
Les phénomènes de dissociation de l’air à haute température sont essentiels car ils sont fortement endothermiques, de sorte que la température de l’écoulement et les flux de chaleur à la paroi sont beaucoup plus faibles que ceux déterminés sans les prendre en compte.
Stabilité et transition
Le passage du régime laminaire au régime turbulent, appelé transition, s’effectue souvent par un phénomène d’instabilité. Sur un profil d’aile en configuration bidimensionnelle stationnaire, l’écoulement est laminaire près du bord d’attaque. En aval, à partir d’un certain point, les lignes de courant ondulent. L’écoulement est devenu instationnaire. Les ondes sont d’abord bidimensionnelles et parallèles au bord d’attaque. Des phénomènes complexes prennent place ensuite pour conduire l’écoulement au régime turbulent. L’analyse théorique de la première phase de transition (ondes de Tollmien-Schlichting) est étudiée à l’aide de l’équation d’Orr-Sommerfeld. Les équations de Navier-Stokes sont développées en petites perturbations. La perturbation de la fonction de courant est mise sous la forme:
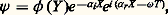
où les grandeurs sont adimensionnées à l’aide d’une longueur face=F9796 l liée à l’épaisseur de couche limite et d’une vitesse de référence V 0.
Avec l’hypothèse que l’écoulement de base est parallèle on obtient:
Cette équation permet de prévoir si l’écoulement de base, défini par son profil de vitesse U (Y ) et le nombre de Reynolds Re , est stable ( 見 i 礪 0) ou instable ( 見 i 麗 0) pour une perturbation de fréquence et de nombre d’onde donnés. Les résultats de cette théorie sont très bien confirmés par l’expérience et servent à établir des critères de transition. Ces critères reposent sur le calcul du taux d’amplification des ondes les plus instables; la transition se produit lorsque ce taux atteint un seuil critique déterminé empiriquement.
L’équation d’Orr-Sommerfeld montre que le nombre de Reynolds joue un rôle essentiel sur la stabilité de l’écoulement laminaire et donc sur la transition. Toutefois, il est loin d’être le seul paramètre qui gouverne la transition. Un gradient de pression positif, la rugosité de la paroi, la préturbulence de l’écoulement ont tendance à produire la transition à un nombre de Reynolds plus faible. La compressibilité, la température de la paroi ont aussi des rôles importants. En tridimensionnel, sur une aile en flèche par exemple, les phénomènes sont plus complexes. En particulier, l’écoulement secondaire créé dans la couche limite peut conduire à des instabilités lorsque l’écoulement est accéléré, même au voisinage du bord d’attaque. En outre, la couche limite turbulente se développant sur le fuselage peut perturber la couche limite qui s’écoule le long du bord d’attaque; elle devient turbulente et contamine toute la couche limite de l’aile.
Couches limites turbulentes stationnaires bidimensionnelles
Couches limites incompressibles
Deux régions sont distinguées dans la couche limite turbulente:
– La région de proche paroi est étudiée à l’aide des variables de paroi y + = yU size=1精 / 益 et U + = U /U size=1精 . L’échelle de longueur visqueuse 益 /U size=1精 est formée à partir de la vitesse de frottement U size=1精 = 連 精 p/ 福 où 精 p est la contrainte de frottement pariétale. Cette échelle caractérise l’épaisseur dans laquelle la tension visqueuse est prédominante devant la tension turbulente.
– La région extérieure est caractérisée par l’échelle de vitesse U size=1精 et l’échelle de longueur 嗀 , qui est l’épaisseur de la couche limite.
L’expérience et des considérations théoriques reposant notamment sur la théorie des développements asymptotiques raccordés montrent que le profil de vitesse dans la région interne suit une loi universelle U + = f (y +). Cette loi est universelle dans le sens où elle ne dépend pas des conditions dans lesquelles évolue la couche limite (nombre de Reynolds, gradient de pression). Pour les faibles valeurs de y + (y + 麗 3), on a U + = y +; quand y + est grand devant l’unité (y + 礪 50), la loi de paroi prend une forme logarithmique:
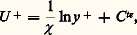
où 﨑 et C te sont des constantes déterminées empiriquement: 﨑 = 0,41, C te = 5.
Ce résultat est essentiel car tous les modèles de turbulence sont recalés de façon à le satisfaire.
Pour établir ces modèles qui servent à résoudre les équations de la couche limite (11 et 12), la turbulence est schématisée à l’aide de la notion d’échelle (vitesse, longueur, temps). Deux classes de structures turbulentes jouent un rôle important: les grosses structures caractérisées par les échelles u , face=F9796 l et et les structures dissipatives caractérisées par v , 兀 et 精 . L’ordre de grandeur de u est la racine carrée de l’énergie cinétique de turbulence; l’ordre de grandeur de face=F9796 l dans une couche limite, la distance à la paroi y pour les régions proches de la paroi; elle est de l’ordre de 嗀 pour la région extérieure. Le taux de dissipation 﨎 représente la quantité d’énergie cinétique de turbulence k transformée en chaleur par unité de temps. Il sert notamment à évaluer les échelles des structures dissipatives (échelles de Kolmogorov):
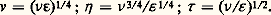
Ces échelles sont telles que le nombre de Reynolds v 兀 / 益 est d’ordre 1.
Le schéma de turbulence le plus simple est établi en écrivant que le rapport de cause à effet qui lie l’écoulement moyen aux grosses structures nécessite que les échelles de temps des deux phénomènes soient du même ordre de grandeur. On a ainsi:
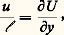
où u / face=F9796 l représente l’inverse de l’échelle de temps de la turbulence, et 煉U / 煉y celui du cisaillement de l’écoulement moyen. D’autre part, l’expérience montre que le coefficient de corrélation entre u et v est bon. On obtient alors le schéma de longueur de mélange de Prandtl:
La longueur l représente une échelle de longueur. Près de la paroi, elle est proportionnelle à la distance à la paroi, et pour retrouver la loi logarithmique de paroi on doit avoir l = 﨑 y . Dans la région externe, l est proportionnelle à 嗀 (l = 0,085 嗀 ). En fait, au voisinage immédiat de la paroi ce modèle doit être corrigé pour tenir compte des effets de paroi et de viscosité sur la turbulence.
Ce modèle est bien adapté au calcul des couches limites, mais l’expression de l doit être modifiée pour les sillages ou pour les jets, par exemple. Des modèles plus généraux font appel à des équations de transport des caractéristiques de la turbulence (par exemple, l’énergie cinétique de turbulence k et son taux de dissipation 﨎 ). Ces équations sont obtenues à partir des équations de Navier-Stokes après quelques manipulations algébriques. Les équations exactes ainsi déduites ne sont pas directement utilisables, car elles font intervenir de nouvelles corrélations, et elles nécessitent une modélisation. Un modèle couramment employé est le modèle k 漣 﨎 . On admet que 﨎 est très voisin du flux d’énergie qui se transmet des grosses aux petites structures. Or, ce flux est gouverné par des mécanismes non visqueux. On relie alors 﨎 aux échelles de turbulence des grosses structures: 﨎 黎 u 3/ face=F9796 l. En remplaçant face=F9796 l dans le schéma de longueur de mélange, on obtient:
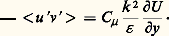
Les équations modélisées pour k et 﨎 sont:
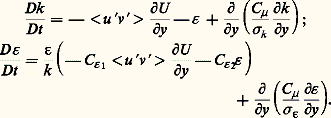
Ce modèle est valable dans la région externe de la couche limite. Près de la paroi, il doit être modifié ou remplacé par le modèle de longueur de mélange approprié.
Les constantes (C ) intervenant dans ces équations sont déterminées à l’aide de résultats expérimentaux. En particulier, les propriétés de la région logarithmique de paroi sont utilisées.
Couches limites compressibles
Le flux de chaleur turbulent doit être exprimé par un modèle. Pour les couches limites, il est souvent admis que le nombre de Prandtl turbulent est constant. Celui-ci est défini par:
La valeur couramment admise est Pr t = 0,89.
Des équations de transport pour le flux de chaleur turbulent peuvent également être établies. Pour un nombre de Mach inférieur à 5, les modèles proposés en incompressible pour la couche limite dynamique restent valables.
Des résultats approchés analogues à ceux du régime laminaire sont obtenus en faisant Pr = 1 et Pr t = 1.
Contrôle de la couche limite
Maintien du régime laminaire
Sur une aile d’avion, l’intérêt de maintenir le régime laminaire sur un parcours assez long réside dans la possibilité d’une réduction de frottement pariétal importante par rapport au régime turbulent. Sur un avion de transport transsonique, la laminarisation des ailes et de la dérive conduit à une réduction de traînée de l’avion de l’ordre de 10 à 15 p. 100. Les moyens pour y parvenir consistent à dessiner des formes d’ailes donnant des gradients de pression appropriés ou à appliquer une aspiration pariétale de la couche limite à travers une paroi perméable.
Moyens d’éviter le décollement
Il est possible d’éviter le décollement en agissant sur ses causes. L’intensité du gradient de pression positif défavorable sera beaucoup atténuée par un profil «aérodynamique» du corps. L’aspiration à travers la paroi fera disparaître les couches lentes, pauvres en énergie cinétique. Un soufflage tangentiel dans le sens de l’écoulement, en revanche, leur communiquera de l’énergie.
Le brassage intense entre filets fluides dans une couche limite turbulente fournit beaucoup plus d’énergie cinétique aux filets proches de la paroi que l’échange moléculaire dans une couche limite laminaire. La couche limite turbulente résiste donc bien mieux au gradient de pression positif et décolle plus tard que la couche limite laminaire soumise au même gradient de pression. Dans certains cas, un déclenchement artificiel de la transition réduit la traînée totale d’un corps ou accroît sa portance dans des proportions considérables, par suite du recul du décollement.
Protection thermique des surfaces
Les corps en vol supersonique et surtout hypersonique doivent être bien protégés contre l’échauffement cinétique.
À cet effet, le corps peut être revêtu d’une couche protectrice qui se consume par ablation. La chaleur transmise à ce «bouclier thermique» est évacuée par la liquéfaction ou la sublimation du matériau utilisé (graphite, verre, matière synthétique).
Un autre moyen de protection consiste à injecter un fluide froid (liquide ou gazeux) dans la couche limite à travers la paroi.
Le rayonnement de la surface peut également contribuer à l’évacuation de la chaleur reçue par la paroi.
Jets, sillages, couches de mélange
Ces écoulements jouent également un rôle important en aérodynamique et de nombreuses études expérimentales leur sont consacrées. Leur calcul relève des mêmes techniques que la couche limite. Cependant l’existence de structures cohérentes leur donne des particularités que les simulations numériques directes (ou les simulations des grosses structures) permettent d’analyser finement.
3. Méthodes numériques
Le développement extraordinaire de l’informatique a entraîné pour les sciences de l’ingénieur, et particulièrement pour l’aérodynamique, une révolution dans les méthodes d’étude théorique. Cette révolution, que l’on peut faire remonter au début des années soixante, a conduit à l’émergence d’une nouvelle discipline, l’aérodynamique numérique, qui joue un rôle de plus en plus important dans la conception et l’optimisation des véhicules ou engins aériens.
Le développement de l’informatique et des méthodes numériques en aérodynamique a eu deux sortes de conséquences, D’une part, des théories simplifiées (théories linéarisées, théories asymptotiques comme celle de la couche limite) ou des méthodes plus exactes bien connues dans leur principe (méthodes des singularités, méthodes des caractéristiques) ont vu leur champ d’applications considérablement élargi. D’autre part, des problèmes, jusque-là inaccessibles à cause de leur complexité mathématique (par exemple, le calcul des écoulements transsoniques et des ondes de choc, ou le calcul d’écoulements fortement décollés), ont pu être résolus numériquement à l’aide de nouvelles méthodes.
Complexité des problèmes d’aérodynamique
La détermination théorique des écoulements autour de véhicules ou d’engins, et plus généralement autour d’obstacles, se heurte à des difficultés variées qui tiennent aussi bien aux caractéristiques des équations à résoudre (équations non linéaires, fortement couplées, de type mathématique variable) qu’à la complexité même des écoulements auxquels on a affaire (complexité géométrique des obstacles, diversité des conditions aux limites parfois délicates à définir, champs illimités, effets physiques avec des échelles de longueur et/ou de temps très différentes). En particulier, la très faible viscosité des fluides usuels tels que l’air et l’eau (qui se traduit par de très grandes valeurs du nombre de Reynolds) conduit à l’existence de couches visqueuses minces, comparées aux dimensions de l’obstacle, et de surfaces de quasi-discontinuité des propriétés de l’écoulement (les ondes de choc).
En conséquence de la complexité mathématique des problèmes, l’existence et l’unicité de la solution ne peuvent être démontrées qu’avec des hypothèses restrictives peu applicables à des problèmes réels d’aérodynamique. Une connaissance expérimentale préalable du problème est toujours indispensable à sa formulation mathématique.
Parmi les facteurs qui contribuent à la complexité des écoulements, il convient de faire une place à part à la turbulence, présente dans la plupart des problèmes d’aérodynamique. En effet, bien que les équations de Navier-Stokes soient valables pour décrire la turbulence, la prise en compte de toutes les échelles des fluctuations turbulentes exige une discrétisation spatio-temporelle tellement fine que le calcul complet d’un écoulement turbulent réel n’est possible que dans des situations physiques très simplifiées et au prix de centaines d’heures de calcul sur un ordinateur puissant. Comme une description statistique de la turbulence est en général suffisante, les méthodes de calcul actuelles portent sur la résolution des équations moyennées ou filtrées qui régissent un écoulement moyen. On sait que ces équations font apparaître de nouvelles grandeurs inconnues (termes de corrélation, comme les tensions de Reynolds) qui nécessitent des relations supplémentaires, soit algébriques, soit aux dérivées partielles, constituant ce qu’on appelle un modèle de turbulence. La modélisation de la turbulence reste un problème ouvert, d’une grande importance pratique, dont dépend pour une part la fiabilité des prévisions numériques.
Diversité des méthodes numériques
La diversité des méthodes numériques utilisées en aérodynamique va de pair avec celle des problèmes d’écoulement et avec celle de leurs formulations mathématiques.
Pour caractériser les divers types de méthodes, considérons le problème continu représenté symboliquement par les équations et conditions (14) du tableau, où f est l’ensemble des inconnues scalaires (f 1, f 2, ..., f L ), fonctions des variables X = (X 1, X 2, ..., X R ) dans un domaine 阮 de frontière 嗀 阮; 硫f = 0 représente le système des équations à résoudre et 暈f = g celui des conditions aux limites. Toute méthode de résolution numérique de ce problème continu comporte une phase de discrétisation (ou phase d’approximation) et une phase de résolution.
La phase de discrétisation transforme le problème continu en un problème discret, c’est-à-dire un problème dont l’inconnue p appartient à l’espace de dimension finie RM , soit p = (p 1, p 2, ..., p M ) où les p m sont des nombres réels. La donnée de p doit définir une approximation 﨏 de f ; autrement dit, on fait le choix d’une représentation approchée de f (X ) par 﨏 (X , p ), fonction donnée de X et de p . Les équations et conditions (14) sont approchées par des équations et conditions discrètes (15) qui, appliquées à 﨏 , donnent un système (16) de M équations pour les M inconnues p 1, p 2, ..., p M .
La phase de résolution porte sur la détermination de la solution p des équations discrètes (16). La résolution est dite directe si elle est effectuée avec un nombre fini d’opérations; elle est dite itérative si la solution p est obtenue asymptotiquement à la limite d’une suite infinie d’opérations, nécessairement tronquée en pratique. Même s’il existe une méthode de résolution directe, une méthode itérative peut être plus efficace et exiger en pratique moins d’opérations.
À partir de ces considérations générales, on peut caractériser les grands types de méthodes de la façon suivante.
Méthodes de singularités
L’équation 硫f = 0 étant supposée linéaire, on choisit pour 﨏 une solution exacte de cette équation construite par superposition de certaines solutions fondamentales (appelées «singularités») qui dépendent de paramètres; l’ensemble de ces paramètres définit les inconnues discrètes p . Il s’agit donc d’un cas spécial où le système discret (16) résulte de la seule discrétisation des conditions aux limites, l’équation 硫 﨏 = 0 étant vérifiée exactement, ce qui présente l’avantage de réduire considérablement le nombre M d’inconnues discrètes nécessaires.
Méthodes de différences finies
Les équations du problème continu sont prises sous la forme d’équations aux dérivées partielles. Le domaine 阮 est discrétisé par un ensemble de points («nœuds») définis en général par les intersections de familles de lignes ou de surfaces qui constituent un maillage. Les inconnues p sont les valeurs de 﨏 aux nœuds; le problème discret résulte de l’application de l’équation 硫 﨏 = 0 et des conditions aux limites 暈 﨏 = g aux nœuds du maillage respectivement dans 阮 et sur 煉 阮. En pratique, la dépendance de 﨏 par rapport à X n’est pas donnée explicitement; elle résulte implicitement (sans d’ailleurs être unique) des formules aux différences finies utilisées pour représenter les dérivées de 﨏 aux nœuds, formules déduites de développements en série de Taylor. Sauf cas spéciaux, on peut considérer que 﨏 est un polynôme en X continu et dérivable par morceaux.
Méthodes de volumes finis
Le problème continu est formulé en termes d’équations de bilan (lois de conservation) sous forme intégrale s’appliquant à des sous-domaines quelconques de 阮. Le domaine 阮 est discrétisé par des volumes élémentaires (ou cellules, ou volumes finis) pouvant se recouvrir partiellement, et le plus souvent définis par des maillages comme dans les méthodes de différences finies. Les inconnues p peuvent être les valeurs moyennes de 﨏 dans chaque cellule, ou plus généralement des valeurs de 﨏 en certains points de chaque cellule. Les équations discrètes résultent de l’application à 﨏 des équations de bilan dans chaque cellule.
Méthodes d’éléments finis
Le problème continu est pris sous une formulation variationnelle, s’il en existe une, ou plus généralement sous une formulation faible. Cette dernière revient à écrire que 硫f est orthogonal à un certain espace 劉T de fonctions-tests 祥 , soit symboliquement:
Le domaine 阮 est discrétisé par des volumes élémentaires (ou cellules, ou éléments finis) – notons e k l’un d’eux – dans chacun desquels 﨏 a une représentation explicite assez simple du type:
Les fonctions 淋 j k , appelées fonctions de forme, sont le plus souvent des polynômes par rapport à une variable Y déduite de X par une transformation de e k en un élément de référence. En général, les a j k sont reliés aux valeurs de 﨏 et éventuellement de ses dérivées en des points particuliers de e k . Les inconnues p sont donc l’ensemble des a j k .
Le problème discret s’obtient soit en substituant 﨏 à f dans la formulation variationnelle du problème continu, soit en écrivant que 﨏 vérifie la formulation faible (17) pour un sous-ensemble fini de fonctions-tests (méthode des résidus pondérés).
Les équations de bilan qui sont utilisées dans les méthodes de volumes finis peuvent être obtenues à partir d’une formulation faible de type (17) où les fonctions-tests 祥 sont les fonctions caractéristiques d’une famille infinie de sous-domaines de 阮 (la fonction caractéristique d’un sous-domaine d 1 prend la valeur 1 si X 捻 d 1, 0 autrement). On peut donc considérer que les méthodes de volumes finis ne sont qu’une classe particulière de méthodes d’éléments finis utilisant comme fonctions-tests 祥 k les fonctions caractéristiques des éléments finis e k . La distinction s’est établie en pratique pour des raisons historiques, les méthodes de volumes finis s’étant développées initialement pour des systèmes d’équations de conservation du premier ordre, et les méthodes d’éléments finis pour des équations du second ordre de type elliptique.
Méthodes spectrales
Ces méthodes sont caractérisées par la représentation de 﨏 (dans 阮, ou dans des sous-domaines macroscopiques de 阮) sous la forme d’un développement par rapport à des fonctions de base 淋 (r )(X r ) pour chacune des composantes de X . Supposant que 阮, ou le sous-domaine considéré, soit un cube, on écrit:
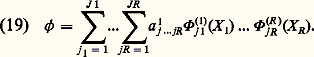
Les inconnues discrètes p sont l’ensemble des coefficients a j 1 ... jR . Les équations discrètes s’obtiennent à partir de (19) par l’une quelconque des approches utilisées dans les autres types de méthodes.
Convergence
Dans toutes ces méthodes se pose le problème théorique de la convergence de 﨏 vers f lorsque la discrétisation est rendue de plus en plus fine, le nombre M d’inconnues discrètes augmentant indéfiniment. Cette question fondamentale, à laquelle on ne peut répondre de façon complète et rigoureuse que pour des problèmes modèles simplifiés, est du domaine de l’analyse numérique (cf. analyse NUMÉRIQUE). On notera que dans les méthodes spectrales, la discrétisation est affinée en augmentant les nombres des termes J 1, ... JR des développements de type (19), chaque sous-domaine où s’applique un tel développement restant fixé, alors que dans tous les autres types de méthodes, le raffinement de la discrétisation est obtenu en diminuant de plus en plus la taille des mailles ou des cellules, le schéma local de discrétisation pour une maille ou une cellule restant fixé.
Méthodes de type mixte
Les définitions générales ci-dessus ne distinguent pas, dans X , la variable temporelle t et les variables spatiales x = (x 1, x 2, x 3) qui peuvent être des coordonnées curvilignes quelconques. En pratique, cette distinction est importante; on considère séparément la discrétisation du temps et la discrétisation de l’espace, qui peuvent être de types différents. Ainsi, on pourra avoir une discrétisation de type différences finies en temps (cas usuel) et de type éléments finis ou de type spectral en espace. Il est même possible de mettre en œuvre des discrétisations de types différents selon la variable d’espace, par exemple de type différences finies en x 1, x 2 et de type spectral en x 3.
Domaines d’application
Méthodes de singularités
Elles sont adaptées au calcul des écoulements incompressibles «irrotationnels», et plus généralement au calcul approché des écoulements compressibles de fluide parfait en théorie linéarisée. L’équation à laquelle obéit, dans ces conditions, le potentiel des vitesses est linéaire, de type équation de Laplace ou équation des ondes. Les solutions fondamentales, dont la superposition donne le potentiel de perturbation qui s’annule à l’infini, sont des sources ou des doublets répartis sur la surface de l’obstacle qui est discrétisée au moyen de facettes, en général quadrangulaires ou triangulaires.
Il est essentiel de tenir compte de l’existence, dans les écoulements réels, de nappes ou de zones tourbillonnaires prenant naissance aux parois (décollements), et dans lesquelles l’écoulement est rotationnel. Ces zones sont discrétisées au moyen de filaments tourbillonnaires concentrés, ou de particules tourbillonnaires concentrées, qui sont autant de singularités «libres» dont les effets doivent être ajoutés à ceux des singularités «liées» à l’obstacle. Le calcul des positions en fonction du temps de ces singularités libres, ou la recherche de leurs positions d’équilibre en régime stationnaire, peut accroître considérablement les temps de calcul; il est possible, pour le traitement de configurations complexes, de figer ces singularités dans des positions approximatives. La figure 8 montre l’application d’une telle méthode à un avion Airbus au décollage.
Méthodes de différences finies et méthodes de volumes finis
Ces méthodes ont été les premières à atteindre un stade de développement avancé pour les calculs d’écoulements stationnaires ou instationnaires, avec prise en compte complète des effets de non-linéarité et de compressibilité, et avec prise en compte partielle (en théorie de la couche limite) ou complète (à l’aide des équations de Navier-Stokes éventuellement moyennées) des effets de la viscosité et de la turbulence (dans le cadre d’un modèle de turbulence).
Les progrès importants réalisés avec ces méthodes ont plus spécialement porté sur les problèmes suivants:
– Calcul des écoulements transsoniques de fluide parfait, soit par résolution de l’équation complète du potentiel (prise en compte de chocs faibles), soit par résolution du système des équations d’Euler instationnaires (prise en compte des chocs vérifiant les relations de Rankine-Hugoniot).
– Calcul des écoulements supersoniques de fluide parfait par résolution du système des équations d’Euler stationnaires. La méthode classique des caractéristiques, qui est une méthode de différences finies particulière, est très efficace pour les écoulements bidimensionnels; mais elle a été supplantée, pour les problèmes complexes, par exemple tridimensionnels ou comportant plusieurs chocs et surfaces de glissement, par des méthodes générales de différences finies ou de volumes finis en maillage fixe non lié aux caractéristiques.
– Calcul des écoulements de fluide visqueux, incompressible ou compressible, soit par résolution d’équations de la couche limite (ou d’équations moins simplifiées) et par des techniques de couplage entre fluide parfait et fluide visqueux, soit par résolution des équations de Navier-Stokes (moyennées pour le cas turbulent).
La figure 9 illustre le calcul de l’écoulement transsonique autour du profil NACA 0012 par résolution des équations de Navier-Stokes moyennées. Tous ces problèmes peuvent être traités en écoulement tridimensionnel, mais le coût du calcul reste un facteur limitatif pour la complexité des applications et pour la précision.
Méthodes d’éléments finis
Ces méthodes ont été développées à l’origine pour le calcul des structures, où elles se montrent très puissantes dans le traitement de géométries complexes. Elles sont particulièrement bien adaptées pour la résolution de problèmes de type principalement elliptique; elles ont d’abord trouvé un domaine d’application privilégié en mécanique des fluides pour de tels problèmes: calcul des écoulements visqueux par résolution des équations de Navier-Stokes, calcul des écoulements transsoniques de fluide parfait par résolution de l’équation complète du potentiel. Elles ont ensuite fait l’objet de nombreux travaux concernant leur application à la résolution des équations d’Euler (fig. 10) ou de Navier-Stokes en fluide compressible et elles couvrent maintenant tous les domaines d’écoulements.
Les méthodes d’éléments finis sont, par conception, bien adaptées à une discrétisation à l’aide de maillages non structurés (tels que des maillages à cellules tétraédriques), et donc au traitement de géométries complexes. Leur généralité et leur «robustesse» en font un outil puissant répondant bien aux exigences des applications à caractère industriel.
Méthodes spectrales
Ces méthodes se caractérisent par un très haut niveau de précision, une grande efficacité liée à l’utilisation de techniques de transformées de Fourier rapides, mais une moins bonne capacité que les autres types de méthodes à prendre en compte des géométries complexes. Ces propriétés font qu’elles ont été développées, depuis quelques années, surtout pour la résolution des équations de Navier-Stokes en vue du traitement numérique direct de la turbulence (avec ou sans modèle de turbulence pour les échelles les plus fines), traitement qui n’est effectivement possible actuellement que pour des cas géométriquement simples. Néanmoins, des recherches se poursuivent pour l’application de ces méthodes à d’autres problèmes, et notamment aux écoulements compressibles et aux ondes de choc.
Quelques aspects particuliers
Ondes de choc et viscosité artificielle
Le calcul des ondes de choc pose un problème difficile, mais essentiel, qui a trouvé une solution tout à fait générale grâce à l’idée de la viscosité artificielle due à J. von Neumann et R. D. Richtmyer (1950). Cette méthode consiste à modifier les équations du fluide parfait en y introduisant un terme jouant le rôle d’une viscosité artificielle, construite de façon à être négligeable en dehors des ondes de choc, et à donner à celles-ci une structure visqueuse artificielle sur une épaisseur de quelques mailles. Ainsi, les discontinuités sont remplacées par des variations continues très rapides. Cette approche est très puissante car elle permet une «capture» automatique des chocs, quel que soit leur nombre. Son inconvénient est d’étaler les discontinuités, ce qui impose d’avoir un maillage assez fin pour limiter l’épaisseur artificielle des chocs.
Il existe une autre approche, dite méthode d’ajustement du choc, dans laquelle le choc est réellement représenté par une surface de discontinuité qu’on suit dans son mouvement et qui vérifie les relations de Rankine-Hugoniot. Cette méthode est très précise, mais sa mise en œuvre est plus complexe et moins générale. Elle permet, par exemple, le calcul précis de l’onde de choc détachée devant un corps émoussé en régime supersonique ou hypersonique.
Écoulements transsoniques potentiels
De nombreux problèmes d’écoulements transsoniques peuvent être décrits par l’équation du potentiel, à condition que les ondes de choc éventuellement présentes restent de faible intensité. Cette formulation a le très grand avantage sur les équations d’Euler de ne faire appel qu’à une seule fonction inconnue scalaire, au lieu de cinq pour les équations d’Euler tridimensionnelles. Cependant, le fait que la nature mathématique de cette équation, dans le cas stationnaire, soit variable, à savoir elliptique en un point subsonique et hyperbolique en un point supersonique, a longtemps constitué un obstacle à sa résolution sauf – exception notable – dans le cadre des méthodes hodographiques.
La solution à cette difficulté est venue de l’idée d’introduire dans le problème discret la règle des signaux interdits, qui s’applique en tout point supersonique, au moyen d’un décentrement du schéma vers l’amont (E. M. Murman et J. D. Cole, 1971), le schéma restant centré aux points subsoniques. Ce principe a ensuite été mis en œuvre sous des formes diverses de type viscosité artificielle.
Écoulements compressibles rotationnels
Les premiers calculs d’écoulements transsoniques avec chocs ont été effectués à partir des équations d’Euler instationnaires, résolues par des méthodes de différences finies explicites. Cette approche instationnaire, outre qu’elle permet de prendre en compte les sauts d’entropie et de rotationnel à travers les chocs, est d’autant plus intéressante que le système d’équations est partout de type hyperbolique, et qu’il est donc possible d’utiliser un schéma de discrétisation unique en subsonique comme en supersonique. Les schémas explicites en temps sont soumis à la condition de stabilité de Courant-Friedrichs-Lewy (1928), condition dite C.F.L. qui limite la valeur du pas de temps et peut conduire à des coûts de calcul inacceptables. Pour le calcul d’écoulements stationnaires, où il n’est pas nécessaire que l’évolution instationnaire de la solution ait une signification physique, on peut modifier la partie instationnaire des équations ou du schéma numérique et accélérer ainsi notablement la convergence vers l’état stationnaire (méthodes pseudo-instationnaires).
L’efficacité des méthodes instationnaires a été également accrue de façon spectaculaire par l’utilisation de schémas implicites en temps qui autorisent des grands pas de temps, mais au prix d’une mise en œuvre plus complexe que celle des schémas explicites.
De grands progrès ont été réalisés sur la précision des méthodes de type instationnaire et sur le contrôle de la dissipation numérique, qu’il s’agisse de viscosité artificielle ajoutée à un schéma centré ou du caractère dissipatif propre d’un schéma centré ou décentré.
Effets visqueux
La prise en compte détaillée des effets visqueux (turbulence incluse), dans le calcul de l’écoulement autour d’une configuration complexe, est rendue possible grâce aux progrès des méthodes de calcul et des ordinateurs, mais la précision des solutions numériques reste tributaire de la validité des modèles de turbulence. Deux grands types d’approche, comportant de nombreuses variantes, sont étudiés. D’abord, l’approche globale consiste à prendre en compte les effets visqueux par résolution des équations de Navier-Stokes (moyennées en turbulent), résolution éventuellement limitée à certaines régions en dehors desquelles on sait a priori que les effets visqueux sont négligeables. Ensuite, l’approche par interaction entre écoulement de fluide parfait et écoulement de fluide visqueux s’applique dans l’hypothèse où ce dernier est limité à des couches minces (couches limites, sillages, zones de mélange) pouvant être décrites par des équations simplifiées susceptibles de techniques de résolution rapides; les deux écoulements sont calculés itérativement en introduisant un couplage entre eux au niveau des conditions aux limites.
Écoulements réactifs
Un important effort de recherche est consacré au calcul des écoulements de gaz réactif tels que ceux rencontrés dans les chambres de combustion ou autour d’engins ou véhicules hypersoniques lors de leur rentrée dans l’atmosphère. La disparité des temps caractéristiques de l’écoulement, d’une part, et des diverses réactions chimiques mises en jeu, d’autre part, peut entraîner un déséquilibre chimique; il faut alors résoudre une équation de conservation de masse pour chaque espèce chimique réagissante. La complexité des équations de la cinétique chimique se traduit par des problèmes de précision et de coût de calcul, problèmes sur lesquels de grands progrès ont été réalisés ces dernières années (fig. 11).
Maillages
La construction de maillages bien adaptés est un élément de plus en plus important pour la précision et l’efficacité du traitement numérique de problèmes complexes. Il est toujours nécessaire pour de tels problèmes, surtout s’ils sont tridimensionnels, de rechercher un compromis entre finesse de maillage, c’est-à-dire précision, et coût de calcul. Ce compromis sera d’autant réussi que le maillage sera bien adapté aux caractéristiques de l’écoulement. Cette adaptation peut être relativement grossière, basée surtout sur les caractéristiques géométriques de l’obstacle et effectuée a priori; ou encore elle peut être plus fine, liée à certaines caractéristiques de l’écoulement inconnues a priori, auquel cas elle doit être automatique et incorporée au processus de résolution (maillages auto-adaptables). L’étude des méthodes de construction et d’optimisation de maillages (structurés ou non structurés) est devenue une branche autonome de l’aérodynamique numérique.
Approche multidomaines
La complexité des formes géométriques et des écoulements ainsi que le souci de développer des méthodes suffisamment générales amènent à rechercher la solution à un problème complexe d’écoulement (l’écoulement autour d’un avion complet) à l’aide d’une approche de décomposition en plusieurs problèmes, chacun d’eux relatif à un domaine ou une partie d’écoulement. Cette approche permet de traiter chaque domaine séparément des autres, aussi bien pour la construction du maillage que pour la formulation mathématique et la méthode numérique. En contrepartie, des procédures de raccord des solutions dans chaque domaine, impliquant une résolution couplée, doivent être mises en œuvre. Cette approche par domaine ouvre la voie vers de nombreuses possibilités qui commencent à être explorées.
4. Souffleries aérodynamiques et moyens d’essai
Les premières mesures relatives à la résistance de l’air sont effectuées au XVIe siècle sur des corps en chute libre. Aux siècles suivants apparaissent la méthode du manège et l’utilisation du vent naturel atmosphérique. En 1884 naît un procédé nouveau reposant sur un concept déjà ancien, puisque la paternité en revient selon toute vraisemblance à Léonard de Vinci: le corps à étudier est soumis à un courant d’air artificiel; c’est le principe des souffleries aérodynamiques.
La première soufflerie connue fonctionne par éjection d’air comprimé, mais quelques années plus tard, entre 1890 et 1910, un ventilateur est utilisé pour produire l’écoulement de l’air, soit en soufflant sur le corps situé à l’extrémité du tunnel, soit en aspirant sur celui-ci. L’aspiration se révèle très rapidement préférable au soufflage; l’écoulement est plus régulier dans l’espace et le temps, car la veine soufflée est animée de mouvements tourbillonnaires. C’est Gustave Eiffel qui, dès 1909, a utilisé dans la soufflerie du Champ-de-Mars, à Paris, les deux organes essentiels qu’on retrouve aujourd’hui dans toutes les souffleries aérodynamiques, à savoir le collecteur et le diffuseur, dont il sera question plus loin.
Les choses ont bien évolué depuis Eiffel. Aujourd’hui, on compte de par le monde plusieurs centaines de souffleries, dont la puissance va de quelques dizaines de kilowatts pour les plus modestes à plus de 100 mégawatts pour les plus importantes.
Les engins concernés par les essais en soufflerie sont en tout premier lieu les avions civils et militaires, mais aussi les missiles, les lanceurs, les hélicoptères, les équipements (sondes embarquées, par exemple), les éléments de turbomachines (grilles d’aubes de compresseur ou de turbine) et enfin les projectiles. En outre, la recherche de meilleures performances, alliée au légitime souci d’économies d’énergie, incite les constructeurs de véhicules navals et terrestres à réaliser aussi des essais aérodynamiques; les bâtiments et ouvrages d’art sont également concernés; et il n’est pas exceptionnel que, lors de la préparation de compétitions importantes, skieurs ou cyclistes recourent aussi aux essais en soufflerie pour expérimenter de nouveaux équipements ou parfaire leur position.
L’exposé qui suit est plus particulièrement consacré au domaine aéronautique et décrit les moyens d’essais et de mesure au sol les plus significatifs utilisés pour les problèmes d’aérodynamique externe. En particulier, il sera fait abstraction des bancs d’essai spécifiques aux turbomachines et aux propulseurs ainsi que des installations très spécialisées (comme, par exemple, celles destinées à l’étude des phénomènes de givrage, des parachutes, des sièges éjectables, etc.).
La philosophie d’utilisation actuelle des souffleries aérodynamiques est telle que, schématiquement, on tend de plus en plus vers deux types d’essais.
Le premier type rassemble les essais de synthèse sur des maquettes de grande taille et dont la géométrie est très proche de la configuration finale (résultat de l’expérience des bureaux d’études et des calculs numériques) allant jusqu’à intégrer les moindres détails des systèmes d’hypersustentation ou de la motorisation (fig. 12). Ces essais sont en général effectués dans les grandes souffleries industrielles, qui sont l’apanage des grands organismes à vocation aérospatiale comme, par exemple, l’O.N.E.R.A. (Office national d’études et de recherches aérospatiales) ou le C.E.A.T. (Centre d’études aéronautiques de Toulouse), en France. Dans le domaine des véhicules terrestres, l’I.A.T. (Institut aérotechnique) de Saint-Cyr gère plusieurs souffleries de taille importante.
Le second type d’essais, de nature fondamentale, a pour objectif principal de constituer des banques de données extrêmement détaillées des grandeurs caractérisant le champ aérodynamique relatif à des configurations bien identifiées. Il s’agit cette fois d’élaborer ou de contrôler les différents modèles théoriques nécessaires à la réalisation des calculs numériques. Les souffleries de laboratoire, dont les dimensions sont le plus souvent modestes, conviennent très bien à ce type d’expérience.
En fait, il existe un large éventail d’études dont les finalités se situent à mi-chemin entre ces deux extrêmes et qui sont généralement menées dans des installations de taille intermédiaire souvent qualifiées de souffleries de recherche (fig. 13).
La réalisation d’essais sur maquette nécessite de satisfaire un certain nombre de conditions de similitude qui permettent, d’une part, de garantir l’équivalence des phénomènes simulés et des phénomènes réels, et d’autre part, de remonter, à partir des résultats de soufflerie, aux grandeurs intéressant le vol. Dans les cas les plus usuels en aérodynamique, il s’agit d’assurer l’égalité du nombre de Reynolds et du nombre de Mach. La distinction des souffleries suivant ce dernier paramètre semble la plus naturelle; elle est d’ailleurs conforme à l’évolution historique, et c’est celle qui sera adoptée après un bref rappel des propriétés fondamentales des écoulements monodimensionnels qui sont indispensables à la compréhension du fonctionnement d’une soufflerie.
Écoulements monodimensionnels
Considérons un tube de courant dont la section évolue lentement (fig. 14); on pourra faire l’hypothèse que, dans toute section normale d’aire A , l’écoulement est homogène et caractérisé par la vitesse V , la pression P , la masse volumique 福 , la température T du fluide. On démontre alors que, dans toute autre section de ce même tube de courant, la connaissance d’un de ces paramètres permet de définir tous les autres. En particulier, dans le cas d’un gaz parfait, la température et la pression dans une section où le nombre de Mach est M , s’expriment simplement en fonction des conditions au repos du gaz (cas limite V0, A秊) appelées température génératrice (T i) et pression génératrice (P i), par les relations suivantes (détente isentropique):
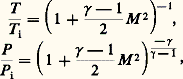
où 塚 est le rapport des chaleurs spécifiques du gaz à pression constante et à volume constant ( 塚 = 1,4 aux températures usuelles pour l’air).
La détente du gaz s’accompagne donc d’un refroidissement croissant avec le nombre de Mach, mais ces relations montrent qu’en régime bas subsonique les évolutions de pression et de température sont faibles et qu’il est possible d’utiliser l’air ambiant comme gaz générateur. En revanche, dès que M excède environ 0,6, il peut en résulter une condensation de la vapeur d’eau éventuellement contenue dans l’air de la soufflerie; il convient donc de l’alimenter en air desséché ou légèrement réchauffé. Aux nombres de Mach plus élevés, le refroidissement peut conduire à liquéfier l’air lui-même; les installations hypersoniques sont donc nécessairement alimentées en air chauffé à un niveau de température T i convenable pour s’affranchir de ce problème.
Une autre relation fondamentale que nous enseigne la théorie des écoulements monodimensionnels est la relation d’Hugoniot, qui exprime, en l’absence de frottement, la variation de la vitesse V du fluide le long du tube de courant de section A où le nombre de Mach est M :
Ainsi, en subsonique (M 麗 1), A et V varient en sens inverse, la vitesse croissant dans des sections convergentes, alors qu’en régime supersonique (M 礪 1), au contraire, la vitesse croît dans des sections divergentes; il s’ensuit aussi que M = 1 ne peut être obtenu que pour dA = 0 et dans une section minimale (le col).
Ces considérations permettent de comprendre les différents régimes de fonctionnement d’une tuyère convergente-divergente (ou tuyère de Laval) suivant la valeur du rapport de la pression à la sortie à la pression génératrice (fig. 15):
– si la pression à la sortie est peu inférieure à la pression P i, l’écoulement qui s’établit dans la tuyère reste subsonique. La vitesse passe par une valeur maximale au col, mais diminue ensuite (courbe a);
– en diminuant cette pression, on obtiendra pour une valeur particulière p , la vitesse du son au col (courbe b);
– pour p 麗 p , p étant la pression donnée par le rapport p /P i pour le nombre de Mach correspondant au rapport de section A s/A c, l’écoulement dans la tuyère est complètement supersonique, et la tuyère est dite «amorcée» (courbe c);
– pour p 麗 p 麗 p , l’écoulement atteint bien la vitesse sonique au col, mais, après un début de détente supersonique, il subit une recompression par choc à l’intérieur de la tuyère (courbe d).
Souffleries aérodynamiques
Souffleries basse vitesse et subsoniques (M size=4麗 0,8)
Le circuit des souffleries subsoniques modernes comprend les éléments suivants, disposés successivement de l’amont vers l’aval (fig. 16):
– le collecteur, partie convergente dans laquelle l’écoulement est progressivement accéléré à partir d’une vitesse faible jusqu’à la valeur recherchée en veine; ce collecteur est précédé de grillages et de filtres antiturbulents pour améliorer la qualité de l’écoulement;
– la veine d’essai où est placée la maquette à l’étude;
– le diffuseur divergent où l’écoulement se recomprime tout en se ralentissant;
– le ou les ventilateurs qui compensent les pertes de charge subies par l’écoulement dans l’ensemble du circuit;
– une canalisation de retour et des aubes directrices qui équipent les coudes du circuit fermé;
– un réfrigérant servant à évacuer toute la puissance fournie par le ventilateur et permettant la régulation de la température de l’écoulement.
Cette disposition en circuit fermé, favorable au rendement énergétique de l’ensemble de l’installation, autorise par ailleurs le contrôle de la pression et du degré hygrométrique de l’air.
Certaines souffleries parmi les plus anciennes, mais dont certaines sont encore en activité, diffèrent du schéma précédent: le fluide accéléré dans le collecteur traverse en jet libre la chambre de mesure, avant de pénétrer dans le diffuseur; malgré les commodités qu’elles offrent au montage des maquettes, les souffleries à veine libre se voient préférer celles à veine guidée, qui permettent une plus sûre évaluation des effets de paroi et ont un meilleur rendement énergétique. Dans certains cas, ces souffleries ne comportent pas de circuit de retour (souffleries de type Eiffel).
Souffleries transsoniques (0,8 size=4麗 M size=4麗 1,2)
Le schéma type d’une soufflerie transsonique diffère peu dans son principe de celui d’une soufflerie subsonique; toutefois, la puissance du ventilateur ou du compresseur mise en jeu est bien plus conséquente (à pression génératrice et section de veine données, la puissance nécessaire varie comme le cube de la vitesse). Fréquemment, à l’aval de la veine d’essai, on trouve un col qui, lorsqu’il est amorcé, a pour fonction d’établir une zone d’écoulement supersonique limitant la remontée des perturbations susceptibles de naître dans le diffuseur, dans le coude ou au niveau du ventilateur.
La réalisation d’un moyen d’essai de maquettes au voisinage de mach 1 pose le délicat problème du blocage de l’écoulement (fig. 17 a); la présence de la maquette dans une veine guidée provoque en effet une diminution locale de section, où s’installe un col sonique qui interdit l’obtention de mach 1 à l’amont de la maquette. Dans une telle situation, l’écoulement sur la maquette n’est manifestement pas représentatif de l’écoulement en atmosphère illimitée relatif au même nombre de Mach à l’amont.
Cette préoccupante question a amené les expérimentateurs à concevoir des veines à parois perméables (munies de perforations ou de fentes longitudinales, fig. 17 c) permettant une expansion transversale de l’écoulement dans les caissons qui l’entourent et à développer les théories complexes qui s’y rapportent. Ce type de veine présente également l’avantage de réduire l’intensité des perturbations qui sont émises par la maquette, puis réfléchies par la paroi et qui peuvent retomber sur celle-ci (fig. 17 b).
Une solution efficace à ce problème des effets de parois, particulièrement sensible en transsonique, mais également présent en subsonique, consiste à donner aux parois de la soufflerie la forme qu’auraient les lignes de courant à la même distance de la maquette si celle-ci était placée en atmosphère illimitée (fig. 17 d). Ce concept, connu sous le nom de «parois adaptables», date en réalité des années 1935-1940, mais n’a pu effectivement voir le jour que vers 1970-1975, car sa mise en œuvre requiert qu’on dispose, sur le site même de la soufflerie, de méthodes numériques fiables et de moyens de calcul puissants. Ce concept est désormais bien au point pour les essais bidimensionnels (fig. 18), mais se heurte à des difficultés d’ordre technique pour les écoulements tridimensionnels, qui font que le recours à des solutions approximatives est, dans ce cas, indispensable.
Un autre problème, particulièrement important en transsonique, est celui de la reproduction correcte des nombres de Reynolds de vol. Au prix de sérieuses difficultés technologiques, tant sur le plan de leur conception que sur celui des moyens de mesure à mettre en œuvre, la solution idéale à cette question réside dans les grandes souffleries cryogéniques, dans lesquelles on crée un écoulement à très basse température (par injection d’azote liquide dans le circuit) et à pression modérée (quelques bars); on agit ainsi sur chacune des variables intervenant dans la définition du nombre de Reynolds. La soufflerie transsonique européenne de Cologne, E.T.W. (European Transonic Windtunnel) construite conjointement par la France, l’Allemagne, la Grande-Bretagne et les Pays-Bas, a été conçue à cet effet.
Souffleries supersoniques (1,2 size=4麗 M size=4麗 5)
Une soufflerie supersonique comporte les éléments suivants:
– un réservoir amont, où le fluide est au repos, ou, dans le cas d’un circuit fermé, un compresseur (mieux adapté que le ventilateur des souffleries subsoniques);
– une tuyère convergente-divergente, dont le profil assure l’uniformité de l’écoulement dans la zone d’expérience (fig. 19);
– un second col de section réglable, suivi d’un diffuseur, l’un et l’autre, destinés à recomprimer l’air du mieux possible avant son évacuation à l’air libre ou son admission dans le compresseur.
Dans une tuyère supersonique amorcée, le nombre de Mach ne dépend, pour un gaz donné, que de la géométrie de la tuyère. La méthode des caractéristiques (cf. supra, Considérations théoriques ), applicable aux écoulements de fluides parfaits, couplée à une méthode de calcul de couche limite (cf. supra, Viscosité: concept de couche limite ), permet de déterminer la forme des tuyères. On réalise le plus souvent des tuyères à section rectangulaire et parois latérales planes (fig. 20) pour les raisons suivantes:
– facilité de réalisation en deux demi-tuyères opposées;
– variation éventuelle de la «géométrie» par pivotement ou translation, en vue de réaliser une petite variation du nombre de Mach autour de la valeur nominale pour laquelle la tuyère a été calculée;
– raccord et réglage aisé du second col servant à améliorer le taux de récupération de la pression.
Certaines souffleries supersoniques possèdent des tuyères dites à mach variable, qui comportent des parois haute et basse flexibles et dont la forme peut être adaptée, sur une large plage, au nombre de Mach désiré à l’aide d’un système de vérins. La réalisation de telles tuyères est cependant délicate en raison des très grandes précisions qu’il faut atteindre sur les déplacements pour obtenir un écoulement de qualité sur toute la plage de variation visée.
Dans l’immense majorité des installations à fonctionnement continu, le ventilateur ou le compresseur est entraîné par un moteur électrique; toutefois, dans le cas des souffleries subsoniques et supersoniques de l’O.N.E.R.A. de Modane, cet organe est remplacé par des turbines Pelton alimentées par une importante chute d’eau. Dans quelques rares cas, l’air du circuit est mis en mouvement grâce à un effet d’entraînement produit par des «trompes» alimentées avec de l’air comprimé emmagasiné dans des réservoirs (souffleries à induction).
Souffleries hypersoniques (M size=4礪 5)
Les problèmes posés par le vol des planeurs hypersoniques, des engins balistiques et des avions de transport à très grande vitesse justifient l’intérêt des essais aérodynamiques à des nombres de Mach élevés (5 麗 M 麗 18, pour fixer les idées). Dans de telles situations, la similitude nombre de Mach-nombre de Reynolds, qu’on s’efforce à grand-peine de réaliser dans les essais à plus bas nombre de Mach n’est plus suffisante; par exemple, la seule étude des échanges thermiques exige d’imposer une condition de similitude supplémentaire portant sur la température de la maquette et la température de l’écoulement.
La figure 21 précise les conditions génératrices dont il faudrait disposer pour simuler la rentrée des véhicules spatiaux actuels. Aux vitesses de plusieurs kilomètres par seconde considérées, les températures atteintes au voisinage de ces véhicules conduisent à un état physico-chimique de l’air caractérisé par des phénomènes de vibration moléculaire, de dissociation et d’ionisation particulièrement difficiles à reproduire et à étudier.
La nécessité de réaliser des enthalpies génératrices élevées et la difficulté de les produire sont à l’origine de la grande variété des moyens d’essai en hypersonique.
Caractères communs aux souffleries hypersoniques
En hypersonique, les lois de sections conduisent à des dimensions de col si faibles que les tuyères planes se trouvent éliminées au bénéfice exclusif des tuyères de révolution, plus faciles à usiner; par ailleurs, les corrections de couche limite, dont les épaisseurs sont de l’ordre du rayon de la tuyère, deviennent délicates à calculer par la méthode exposée précédemment, si bien que le recours à des programmes de résolution des équations de Navier-Stokes moyennées (cf. supra, Considérations théoriques ) est dans ce cas souhaitable. De plus, les rapports de pression d’amorçage croissent rapidement avec le nombre de Mach, et il faut assurer, outre une augmentation de la pression génératrice, afin d’obtenir des nombres de Reynolds significatifs, des pressions d’extraction très basses obtenues généralement grâce à des réservoirs vidés avant la rafale. En outre, les relations de la détente isentropique ont montré qu’il est nécessaire d’alimenter ces souffleries avec de l’air chaud (environ 1 100 kelvins pour mach 10 et 2 500 K pour mach 16). Les puissances correspondantes deviennent telles que les souffleries hypersoniques sont, sauf exceptions, «à rafales»: l’énergie correspondant à un essai est d’abord emmagasinée sous forme d’air comprimé, par exemple, puis utilisée pendant un temps très court.
Les souffleries «tièdes»
Dans ces souffleries, où est seulement évitée la liquéfaction, la simulation des phénomènes réels du vol hypersonique est loin d’être complètement assurée; elles constituent cependant un outil important pour l’étude des phénomènes intéressant les nombres de Mach élevés.
Dans le cas le plus courant et pour des températures ne dépassant guère 800 K, on dispose en série un réchauffeur et un accumulateur de chaleur – à plaques, ou à billes – (fig. 22); le réchauffage de l’accumulateur est effectué, préalablement à l’essai, par une circulation de gaz chauffé électriquement; cette phase, qui peut être assez longue, ne requiert qu’une puissance modérée. D’autres solutions de chauffage consistent, par exemple, à faire traverser au gaz des conducteurs électriques creux chauffés par effet Joule, au prix de puissances électriques instantanées plus élevées; leur avantage réside dans l’obtention de températures allant jusqu’à environ 1 200 K et dans l’absence des inévitables poussières générées dans les accumulateurs de chaleur.
Les souffleries à haute enthalpie
L’obtention de températures génératrices excédant 2 500 K accompagnées de pressions élevées requiert des puissances considérables; la durée d’une rafale est par suite extrêmement courte, limitée également par la tenue mécanique à haute température des matériaux constituant la partie amont de la tuyère. Dans les souffleries à arc, l’énergie est fournie par un arc électrique jaillissant entre une électrode et la paroi (mise à la masse) d’une chambre préalablement remplie du fluide à échauffer (air ou azote) sous une pression choisie en fonction des conditions finales souhaitées. L’éclatement d’un diaphragme ou l’extrusion d’un obturateur permet l’écoulement du gaz dans la tuyère, où sont réalisés des nombres de Mach allant jusqu’à 20. On obtient ainsi des pressions de quelques milliers de bars et des températures de 3 000 à 8 000 K, pendant des durées utiles de l’ordre de 100 millisecondes. Les énergies nécessaires, avoisinant 10 mégajoules, peuvent être obtenues, par exemple, en transformant en énergie électrique l’énergie cinétique du rotor d’un alternateur et du volant d’inertie qui lui est lié, préalablement mis en rotation rapide (soufflerie F 4 de l’O.N.E.R.A. du Fauga).
En réduisant le niveau de pression, on peut entretenir sous faible puissance l’arc électrique et disposer ainsi d’une soufflerie à plasma pratiquement continue, dont l’intérêt réside surtout dans l’étude d’échantillons de matériaux servant à la protection des engins spatiaux devant rentrer dans l’atmosphère.
Les tubes et souffleries à choc
Des écoulements à pression et enthalpie élevées y sont engendrés par le passage d’une onde de choc dans un long tube cylindrique. Fermé à ses extrémités et divisé en deux enceintes par un diaphragme, le tube est rempli de gaz à haute pression dans une des enceintes et à faible pression dans l’autre; la rupture du diaphragme provoque la formation puis le déplacement d’une onde de choc, qui comprime, échauffe et met en mouvement le gaz initialement à basse pression. La température et la pression de l’écoulement ainsi obtenu dépendent du rapport des pressions initiales dans les deux enceintes et du rapport des vitesses du son des deux gaz; en utilisant dans l’enceinte à haute pression un gaz léger, éventuellement chauffé pour y augmenter la vitesse du son, et de l’air dans l’autre enceinte, on peut obtenir pendant environ 100 microsecondes, de 7 000 à 8 000 K à un nombre de Mach modéré. Pour faire d’un tube à choc un moyen de recherche aérodynamique (soufflerie à choc), on le prolonge par une tuyère où sera alors obtenu un nombre de Mach hypersonique.
Les tunnels balistiques
Dans les tunnels balistiques, on étudie directement le mouvement de maquettes (le plus souvent de formes géométriques simples) tirées à grande vitesse par un canon. Les canons à gaz léger, associés à ces installations, peuvent lancer à 8 km/s des projectiles de quelques grammes et à 4 km/s des projectiles de plusieurs centaines de grammes. Des stations d’observation disposées tout au long du tunnel permettent de restituer la trajectoire et, par dérivations, les forces aérodynamiques sur le projectile. Les visualisations strioscopiques de l’écoulement autour des maquettes, facilitées par le niveau élevé des densités qui règnent en général dans ces tunnels, mettent en évidence les moindres détails de l’écoulement, ainsi qu’en témoigne la photographie d’un sillage turbulent (fig. 23); de même que peuvent être observées les caractéristiques électromagnétiques des gaz chauds entourant la maquette. Quelques mesures internes peuvent également être effectuées grâce à des microémetteurs contenus dans la maquette, en dépit des difficultés de réalisation de circuits électroniques résistant à des accélérations de l’ordre de 106 fois celle de la gravité.
Méthodes et moyens de mesures
Les grandeurs à mesurer dans l’expérimentation aérodynamique ne sont pas de nature fondamentalement différente de celles concernant les autres branches de la physique: forces, moments, pressions étaient effectivement mesurés dans les premières souffleries au moyen des balances, dynamomètres et manomètres existant par ailleurs. Cependant, les techniques ont dû s’adapter au caractère particulier des essais en soufflerie, notamment en évoluant vers les faibles dimensions et vers la réduction des temps de réponse pour s’accorder aux brèves durées des expériences aérodynamiques modernes. L’enregistrement des mesures a suivi les progrès techniques: après avoir été à lecture directe, puis à stylet, puis photographique, il est à présent numérique, et les résultats des essais sont désormais traités par des ordinateurs reliés aux chaînes de mesures (conditionneurs des capteurs, amplificateurs, filtres, convertisseur analogique-numérique). Ces puissants moyens permettent un suivi en temps réel des principaux paramètres, et les résultats finaux sont obtenus très rapidement avec une intervention minimale du personnel.
Les moyens d’investigation utilisés en aérodynamique sont d’une grande variété: les plus courants sont les procédés de visualisation, les mesures de pression, les mesures d’effort, les mesures de vitesse (en module et direction) et les mesures de flux thermique.
Les procédés de visualisation
Ils permettent, par l’observation directe de l’écoulement sur la maquette elle-même ou dans son voisinage, d’expliquer des phénomènes révélés par les mesures, notamment les décollements et la présence de tourbillons. À la paroi, enduits visqueux, fils de laine collés (ou encore fils de Nylon enduits de produit fluorescent) renseignent immédiatement sur l’allure générale de l’écoulement. Une méthode extrêmement didactique consistant à visualiser les lignes de courant par des filets de fumée émis à l’amont de la maquette a trouvé un développement fécond dans les tunnels hydrodynamiques, où l’écoulement est rendu visible par des bulles illuminées au sein du courant liquide ou par l’émission de filets différemment colorés en des points de la maquette: la planche hors texte illustre la richesse des informations recueillies par ce dernier procédé. Une autre méthode, particulièrement utile pour la mise en évidence de tourbillons, consiste à créer un plan de lumière, en général transversalement à l’écoulement et à observer la lumière diffusée par des particules très légères introduites loin en amont, qui le traversent.
Aux plus grandes vitesses, et notamment à partir de mach 0,8, sont mises en œuvre des méthodes optiques qui, au moyen de montages spéciaux, mettent en évidence les variations de l’indice de réfraction de l’écoulement n , liées à celles des masses volumiques locales 福 par la loi de Gladstone-Dale: (n 漣 1)/ 福 = C te (fig. 24); de remarquables visualisations peuvent ainsi être obtenues (fig. 23 et 25). Le faible niveau des masses volumiques dans les souffleries hypersoniques rend peu sensibles ces méthodes au-delà des nombres de Mach 12 à 14, où ne sont plus visibles que les chocs intenses; pour des densités suffisamment faibles, on peut provoquer la luminescence au sein de l’écoulement par décharges électriques, champ à haute fréquence ou bombardement électronique et observer sous forme d’un accroissement de luminosité les ondes de choc et autres singularités.
Les mesures de pression et la détermination des conditions de référence soufflerie
Les progrès techniques ont fait abandonner les manomètres à liquide au bénéfice des capteurs piézo-électriques, des capteurs utilisant un résonateur à cristal de quartz ou plus souvent des capteurs à membrane. Le principe de ces derniers consiste à mesurer le déplacement de cette membrane par extensométrie (jauges de contrainte rapportées ou diffusées), par variation de capacité ou par variation de self-induction entre deux microbobines. La diminution des temps de réponse amène à écourter le plus possible les tubes disposés entre les prises de pression et les capteurs et à réduire les dimensions propres de ces derniers de façon à pouvoir en disposer le plus grand nombre à l’intérieur des maquettes. L’utilisation de commutateurs pneumatiques, permettant avec un seul capteur de mesurer successivement jusqu’à quarante-huit pressions, est fréquente. Les récents progrès de l’électronique ont permis d’intégrer dans un volume extrêmement réduit (quelques centimètres cubes) un grand nombre de capteurs autorisant des mesures à cadence rapide.
La valeur de la pression génératrice de l’écoulement dans une soufflerie est obtenue à l’aide d’un capteur installé dans la chambre de tranquillisation (où la vitesse de l’écoulement est quasi nulle) ou connecté à une antenne de Pitot placée en veine. Ce type de sonde consiste en un simple tube, d’extrémité généralement hémisphérique, disposé parallèlement à la vitesse (fig. 26 a). En subsonique, les deux procédés fournissent des résultats équivalents, mais en supersonique un tel pitot mesure la pression d’arrêt à l’aval du choc, localement assimilable à un choc droit, qui se forme devant lui. La connaissance de la pression Pitot et de la pression génératrice déterminée par la première méthode permet de remonter au nombre de Mach à l’endroit de la sonde.
La mesure de la pression statique est réalisée en disposant convenablement des orifices de pression de faible diamètre, percés perpendiculairement à l’axe du pitot (fig. 26 a) ou bien encore à la paroi même de la soufflerie ou de la maquette. Puisque dans la couche limite le gradient de pression normal à la paroi est nul, la pression pariétale est donc égale à la pression de l’écoulement potentiel. La connaissance de la pression statique et de la pression génératrice permet de remonter au module de la vitesse locale de l’écoulement, grâce à la relation de Bernoulli en incompressible (cf. supra, Considérations théoriques ), ou au nombre de Mach, grâce à la relation de la détente isentropique en compressible (dans ce cas, le calcul de la vitesse nécessite également une mesure de température). En supersonique, on peut recourir à des sondes du type de celle de la figure 26 b pour déterminer la pression statique au sein d’un écoulement.
Mesures d’effort
Pour analyser les trois forces et trois moments de la résultante aérodynamique s’exerçant sur la maquette en essai, on utilise une «balance aérodynamique». Les premières balances, de type mécanique, confiaient à une cinématique complexe la mesure séparée des six composantes; elles ont été remplacées en général par des balances en dard, munies de jauges extensométriques (fig. 20), créées pour les essais transsoniques et supersoniques qui prohibent toute fixation transversale perturbatrice de l’écoulement. La conception, l’usinage et l’équipement de telles balances se révèlent délicats, et leur emploi exige un étalonnage soigné en laboratoire.
Mesure des vitesses
Il a été indiqué plus haut comment pouvait être obtenu le module de la vitesse dans un écoulement; dans les situations où il faut déterminer également sa direction, on utilise très souvent des sondes biseautées du type de celle de la figure 26 c; celles-ci délivrent une différence de pression dont la valeur est étroitement liée à l’inclinaison de l’écoulement dans un plan passant par l’axe de la sonde et les deux orifices de pression. Le principe de la sonde directionnelle, qui vient d’être évoqué, peut être étendu à des sondes d’extrémité conique comportant, en plus du trou central (servant de pitot), quatre, voire six orifices disposés sur la périphérie (fig. 26 d). Ce type de sonde permet de déterminer la vitesse en module et direction jusqu’à des angles de 40 degrés et pour des nombres de Mach allant jusqu’à 4.
La vitesse de l’écoulement peut également être directement mesurée à l’aide d’un dispositif, appelé «fil chaud» (fig. 26 e), qui comporte un fil de tungstène dont la longueur active ne dépasse pas 1 millimètre et dont le diamètre est de quelques micromètres, placé perpendiculairement à l’écoulement; ce fil est chauffé par effet Joule et maintenu à une température rigoureusement constante et supérieure à celle du fluide environnant, grâce à un asservissement électronique. Après étalonnage préalable, la mesure de la tension d’alimentation permet de remonter à la vitesse instantanée de l’écoulement, qui tend à refroidir le fil. L’utilisation de fils chauds croisés ou disposés en pyramide permet la mesure simultanée de plusieurs composantes.
La vélocimétrie laser est, quant à elle, une technique optique de mesure des vitesses locales et instantanées dans les écoulements fluides, et son intérêt principal réside dans le fait qu’aucune sonde matérielle n’est introduite à l’endroit où s’effectuent les mesures. Dans la configuration le plus généralement adoptée, deux faisceaux lasers cohérents entre eux, d’égale intensité, se croisent et sont focalisés dans un petit volume de mesure où est créé un réseau de franges d’interférence (fig. 27). On introduit, très à l’amont de la zone de mesure, des particules très légères et submicroniques qui suivent pratiquement sans aucun retard les accélérations et les décélérations de l’écoulement, ainsi que les fluctuations turbulentes. Chaque particule traversant le volume de mesure «voit» alternativement des franges sombres et brillantes et diffuse un flux modulé à une certaine fréquence; la mesure de cette fréquence et la connaissance de la distance d’interfrange conduisent à la valeur de la composante de la vitesse perpendiculaire aux franges. Les montages à deux ou trois réseaux de franges permettent la mesure simultanée de deux ou trois composantes; la vélocimétrie laser constitue un outil extrêmement précieux pour l’étude de la turbulence.
Mesure des flux thermiques
La détermination des échauffements cinétiques auxquels sont soumis les véhicules hypersoniques fait également appel à des essais en soufflerie. Les mesures de flux thermique sont réputées délicates; cela tient au fait que cette grandeur n’est accessible que par l’effet qu’elle produit, c’est-à-dire une élévation de température. Le fait que la très grande majorité des souffleries hypersoniques aient des durées d’essai tout au plus de quelques dizaines de secondes exige l’utilisation de fluxmètres adaptés aux régimes thermiques transitoires. On distingue les méthodes ponctuelles, qui conduisent à des résultats précis en des points particuliers de la maquette, et les méthodes cartographiques, qui permettent une appréciation beaucoup plus globale des phénomènes, au prix cependant d’une précision moindre.
Dans le premier cas, il s’agit d’appliquer la technique calorimétrique classique en différents points de la maquette ou bien encore de mesurer l’échauffement pariétal à l’aide d’un thermomètre à film de platine ou d’un thermocouple dont la jonction est réalisée précisément à la surface; la détermination du flux thermique en surface repose alors sur la résolution de l’équation de la chaleur.
Diverses méthodes cartographiques sont utilisées: il s’agit, par exemple, d’appliquer, sous forme de peinture, différents revêtements thermosensibles dont la colorimétrie évolue avec la température de façon irréversible (peinture «thermocolor») ou réversible (cristaux liquides), ou bien encore des produits dont la sensibilité thermique est fondée sur le changement de phase de l’un de ses constituants. La thermographie, quant à elle, analyse le rayonnement infrarouge émis par la maquette, et la luminescence utilise la propriété de certains matériaux qui, lorsqu’ils sont excités par un rayonnement ultraviolet, réémettent un spectre visible dont certaines qualités dépendent, entre autres facteurs, de la température. Dans tous les cas, on vise à déduire les flux thermiques à partir des échauffements pariétaux, de la même façon qu’avec les fluxmètres ponctuels.
5. Applications
Les applications pour lesquelles l’aérodynamique joue un rôle important sont nombreuses. Pour les aéronefs, tels que les planeurs, les avions de transport, les avions militaires, les missiles et les véhicules spatiaux, ce sont les forces aérodynamiques qui assurent la sustentation des appareils. Pour d’autres aéronefs, tels que les hélicoptères ou les «convertibles», les forces aérodynamiques assurent à la fois la sustentation et la propulsion.
Pour les turboréacteurs, les statoréacteurs, l’aérodynamique interne du moteur joue un rôle essentiel pour le rendement du système propulsif, et il en est de même de l’aérodynamique des hélices pour les turbopropulseurs et les éoliennes. Si, pour les bateaux à voiles, les forces aérodynamiques assurent la propulsion, elles s’opposent par contre au déplacement des véhicules terrestres. Enfin, les efforts aérodynamiques sont également pris en compte pour le dimensionnement de certains bâtiments et ouvrages d’art.
Coefficients aérodynamiques
Les efforts aérodynamiques s’exercent perpendiculairement à la surface du véhicule ou de l’obstacle (efforts de pression) et tangentiellement à la surface (efforts de frottement). La réduction de ces efforts conduit au torseur des forces aérodynamiques dont les éléments sont une force F et un moment 紐. La projection de ce torseur sur un trièdre lié à la vitesse (fig. 28) et ayant pour origine un point de référence (généralement le centre de gravité) donne six composantes qui sont adimensionnées en utilisant une surface de référence S , une longueur de référence l et une pression de référence 1/2 福 0 V 2 (pression cinétique). L’on définit ainsi six coefficients aérodynamiques qui sont, dans le cas d’un avion sans propulsion (planeur), les coefficients:
L’axe de l’avion est repéré par rapport au vecteur vitesse à l’aide de deux angles, l’incidence 見 (positive quand l’avion est «à cabrer») et le dérapage 廓 (positif quand l’aile droite est avancée) [fig. 28].
Ces coefficients aérodynamiques dépendant de la géométrie du véhicule ou de l’obstacle, du nombre de Mach M 0 = V 0/a (a étant la vitesse du son), du nombre de Reynolds Re = V 0l / 猪 ( 猪 étant la viscosité dynamique de l’air), de la turbulence de l’écoulement, de l’état de surface de la paroi et sa température, etc.
Aérodynamique des profils aux basses vitesses
La section d’une aile d’avion par un plan parallèle au plan de symétrie de l’avion est appelée «profil d’aile». L’écoulement autour d’un profil est dit «bidimensionnel», le vecteur vitesse en un point quelconque étant dans le plan du profil. L’écoulement autour d’un profil est celui qui existerait autour d’une aile d’envergure infinie et sans flèche. Pour les profils, la longueur de référence est la corde 1, et la surface de référence S est le produit de la corde par une largeur unité: S = 1 憐 1 (fig. 29 a). Les performances des profils sont généralement tracées sous la forme de courbes d’évolution des coefficients aérodynamiques (fig. 29 b) C z = f ( 見 ), C z = f (C x ) appelée polaire, C z = f (C m ), le C m étant calculé par rapport à un point de la corde situé à l’abscisse réduite x /l = 0,25. La courbe C z ( 見 ) est sensiblement linéaire aux faibles incidences avec une pente dC z /d 見 力 1/2 神 par radian, cette pente diminue pour les incidences élevées du fait de l’épaississement de la couche limite qui se développe le long de la paroi du profil, et le C z maximum est atteint lorsque cette couche limite «décolle» de la paroi à l’extrados. Pour les profils usuels, les valeurs de C z max sont comprises entre 0,8 et 2 et les incidences de décrochage entre 100 et 200.
Sur la polaire C z = f (C x ), on distingue plusieurs points particuliers. Le point de finesse maximale (C z /C x maximum), le point de traînée minimale, le point de vitesse verticale de descente minimum, qui est important pour les planeurs (C x2/C z3 minimum). Pour un niveau de portance donné, la traînée augmente avec l’épaisseur relative e /l et la cambrure. Le coefficient de traînée minimale des profils classiques est voisin de 0,01, mais il peut être beaucoup plus faible (face=F0019 黎 0,005) pour les profils «laminaires», qui possèdent des répartitions de pressions spécifiques destinées à reculer le plus possible la transition de la couche limite.
La courbe C z = f (C m ) permet d’obtenir la position du centre de poussée (point d’application de la résultante aérodynamique):
et celle du foyer (point d’application de la variation C z de portance due à une variation 見 de l’incidence):
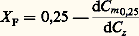
par rapport au point x /l = 0,25. La position du foyer par rapport au centre de gravité traduit la stabilité en tangage. Une configuration sera stable en tangage si le foyer est en arrière du centre de gravité. Pour augmenter la portance maximale des profils, on utilise des dispositifs «hypersustentateurs» au bord d’attaque et/ou au bord de fuite. Les dispositifs de bord d’attaque (cambrure locale, bec à fente) permettent de prolonger la courbe C z = f ( 見 ) à des valeurs plus élevées de C zmax ( C zmax 力 0,5). Les dispositifs de bord de fuite (volet de courbure, volets à fente) augmentent le C z à incidence fixée, mais réduisent l’incidence de décrochage. Ces dispositifs hypersustentateurs augmentent fortement la traînée, ils sont donc amovibles et ne sont utilisés que pour les phases de vol nécessitant de fortes portances (décollage, atterrissage).
Influence du nombre de Mach sur les coefficients aérodynamiques
Lorsque le nombre de Mach augmente, tant qu’il n’y a pas de zones d’écoulement supersonique sur le profil (écoulement subcritique), les théories linéarisées rendent bien compte des évolutions des coefficients aérodynamiques. Ainsi à incidence fixée, le C z et les coefficients de pression
augmentent en valeur absolue avec le nombre de Mach. Au-delà du mach critique (nombre de Mach amont pour lequel on atteint M = 1 en un point du profil), apparaissent des ondes de choc qui modifient les répartitions de pression. Les ondes de choc constituent des recompressions brutales qui épaississent la couche limite et peuvent la faire décoller du profil. La traînée croît alors fortement à partir d’un point appelé «mach de divergence de traînée» et la portance chute pour un nombre de Mach légèrement supérieur appelé «mach de divergence de portance».
Quand le nombre de Mach M 0 est supérieur à l’unité (écoulement supersonique), il se forme en amont du profil une onde de choc courbe avec une zone subsonique limitée par le choc et une ligne sonique et deux ondes de choc apparaissent au bord de fuite (fig. 30). Lorsque M 0 croît, l’onde de choc détachée se rapproche du profil, la zone subsonique diminue, les ondes de choc s’inclinent de plus en plus. Pour ces écoulements supersoniques, la traînée à iso-incidence est plus élevée qu’en subsonique, du fait de la présence de ces ondes de choc (traînée d’onde), dont l’intensité croît avec le nombre de Mach. Les finesses des profils sont faibles en écoulement supersonique. Le centre de pousssée se situe, quant à lui, vers la mi-corde, il recule donc par raport à l’écoulement subsonique. Les coefficients aérodynamiques C z et C x diminuent progressivement lorsque le nombre de Mach M 0 augmente.
Aérodynamique des ailes
Une aile est constituée par l’«empilement» de profils. La forme en plan est la projection de l’aile dans un plan perpendiculaire au plan de symétrie. L’aire de la forme en plan est prise comme surface de référence, et une corde moyenne est utilisée comme longueur de référence. Les principaux paramètres géométriques d’une aile sont son allongement = 4L 2/S , son effilement 﨎 = l /l 0, les angles de flèche de bord d’attaque 淋 BA, de bord de fuite 淋 BF et de la ligne des quarts de corde des profils 淋 m (fig. 31). La loi d’évolution du calage des profils en envergure s’appelle le vrillage de l’aile. Les deux grandeurs géométriques qui influencent le plus les performances aérodynamiques d’une aile sont l’allongement et la (les) flèche(s).
Influence de l’allongement
Du fait de l’envergure limitée et de l’existence, en régime de fonctionnement normal, de surpressions à l’intrados (partie inférieure) de l’aile et de dépressions à l’extrados (partie supérieure), le vecteur vitesse possède une composante transversale dirigée de l’extrémité vers l’emplanture du côté extrados et de l’emplanture vers l’extrémité du côté intrados. Cette différence de direction du vecteur vitesse entre l’extrados et l’intrados, aussi présente en aval du bord de fuite, crée une nappe tourbillonnaire qui «s’enroule» aux extrémités de l’aile pour former les tourbillons marginaux (fig. 32). Elle crée également en un point quelconque de l’écoulement une vitesse verticale dirigée vers le bas (vitesse induite) qui diminue l’incidence effective des profils et génère une force de traînée (traînée induite), même en écoulement non visqueux. Le coefficient de traînée correspondant C xi s’ajoute donc au coefficient de traînée de frottement pour former la traînée totale de l’aile. Le coefficient de traînée induite est fonction de la portance et de l’allongement, et la loi C xi = C z 2/ 神凞 e traduit approximativement son évolution en fonction de ces deux paramètres. Le coefficient e fonction de la forme en plan et du vrillage de l’aile est généralement compris entre 0,9 et 1.
L’incidence induite provoque une diminution de la pente dC z /d 見 des ailes par rapport à celle des profils, diminution d’autant plus forte que l’allongement est faible. Du fait de l’envergure limitée, la répartition du C z des profils en envergure n’est pas uniforme, le C z s’annulant en extrémité de l’aile.
Influence de la flèche
L’effet essentiel de la flèche est de réduire le nombre de Mach effectif de fonctionnement des profils, et par conséquent de repousser à des valeurs plus élevées du nombre de Mach de vol, les troubles transsoniques tels que les divergences de traînée et de portance. Le nombre de Mach effectif devient, selon la théorie de l’effet de flèche, le nombre de Mach normal au bord d’attaque M n = M 0 cos 淋 BA pour une aile non effilée d’allongement infini.
Écoulements tourbillonnaires
Pour des ailes de faible allongement ( 諒 3) et/ou à forte flèche ( 淋 閭 400), des décollements apparaissent à l’extrados dès les faibles incidences, ces décollements s’organisent en tourbillons qui induisent des survitesses et par conséquent des dépressions qui augmentent la portance (fig. 33). Ce supplément de portance appelée «portance tourbillonnaire» est d’autant plus fort que l’allongement est faible et la flèche élevée. Ces tourbillons augmentent d’intensité avec l’incidence. Ils «éclatent» en aval de l’aile aux faibles incidences, mais la position de l’éclatement se rapproche de l’aile lorsque l’incidence croît et lorsque celui-ci a lieu au-dessus de la voilure, il induit des non-linéarités importantes sur les courbes C z ( 見 ) et C z (C m ).
Aérodynamique des planeurs
Pour les aéronefs non motorisés tels que les planeurs, les ailes delta ou les parapentes, il s’agit soit de parcourir la distance maximale à partir d’une altitude de départ, soit de voler le plus longemps possible, c’est-à-dire de voler avec la vitesse verticale de descente le plus faible possible.
La finesse est le paramètre essentiel pour ce type d’appareil; elle varie pour les planeurs actuels entre 30 et 60 selon leur taille. Ces valeurs élevées de finesse sont obtenues grâce à des ailes de grand allongement ( de 20 à 45) pour réduire la traînée induite et à l’utilisation de profils laminaires pour minimiser la traînée de frottement. Ces finesses élevées sont maintenues pour des plages de C z importantes sur les planeurs de classe course ou libre grâce à l’utilisation de volets de courbure.
Pour les ailes delta ou les parapentes, les finesses sont nettement plus faibles (de 5 à 12), parce que les allongements sont plus petits (de 6 à 10 pour les ailes delta, de 3 à 5 pour les parapentes), et aussi du fait de sources de traînées parasites telles que le pilote, les câbles de suspente, et enfin du fait de l’utilisation de profils très minces (toile) et poreux.
Aérodynamique des avions de transport
Les principales performances des avions de transport sont:
– le rayon d’action donnée par la formule de Breguet:
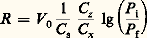
où V 0 est la vitesse de vol, C s la consommation spécifique des moteurs, P i le poids en début de croisière, et P f le poids en fin de croisière, C z /C x étant la finesse;
– la portance maximale et la finesse aux basses vitesses qui conditionnent les longueurs de pistes au décollage et à l’atterrissage, ainsi que la pente de montée de l’avion, cette dernière étant essentielle pour le niveau de bruit de survol au décollage.
Les avions de transport ou d’affaires ont vu leur efficacité énergétique (exprimée en sièges 憐 km/kg de carburant) augmenter considérablement depuis la dernière guerre. Ceci a été obtenu grâce aux progrès réalisés dans la conception du système propulsif (introduction des réacteurs avec des taux de dilution croissants), des structures (diminution des masses) et de l’aérodynamique. Les principales améliorations aérodynamiques ont consisté en:
– l’utilisation de profils performants en transsonique (profils supercritiques);
– l’augmentation de l’allongement des voilures;
– l’amélioration des systèmes hypersustentateurs;
– la réduction des traînées parasites et des traînées d’interférence entre les différents éléments de l’avion.
Les profils supercritiques apparus au début des années 1970 possèdent, par rapport aux anciens profils, de meilleures performances en écoulement transsonique (finesse augmentée) par suite d’un accroissement moins rapide de l’intensité des ondes de choc avec le nombre de Mach de vol (fig. 34). Pour les avions les plus récents, les allongements sont proches de 9, et les flèches voisines de 300 pour un mach de croisière d’environ 0,8 (fig. 35). Les finesses en croisière des avions de transport sont passées de 12 à 20 durant les vingt dernières années. Les C z de croisière sont compris actuellement entre 0,5 et 0,6 et sont de l’ordre de 2,5 à 3 à l’atterrissage et de 1,5 au décollage.
La présence des moteurs et des mâts supports modifie l’écoulement sur l’aile. Cet effet est surtout important à l’intrados de l’aile au voisinage des mâts supports avec création de survitesses pouvant engendrer des ondes de choc et des décollements de la couche limite, d’où une augmentation de la traînée de frottement.
La présence des moteurs engendre une diminution de la portance de l’aile et modifie la répartition des portances locales en envergure, avec accroissement de la traînée induite de l’aile.
Les recherches actuelles au niveau de l’aérodynamique des avions de transport concernent la réduction de la traînée et donc de la consommation de carburant. Les principales sources de traînée étant la traînée induite (face=F0019 力 40 p. 100) et la traînée de frottement (face=F0019 力 50 p. 100), c’est sur ces deux postes que portent les recherches.
Pour ce qui est de la traînée induite, des dispositifs tels que les ailettes de bout d’aile (winglets ) utilisés sur les avions récents (A-320, A-300 600, A-340, MD-11, 747-400) engendrent, du fait de leur orientation, une force de portance s’ajoutant à celle de l’aile et une force de poussée diminuant la traînée (fig. 36).
Pour la traînée de frottement qui représente environ la moitié de la traînée totale de l’avion, deux voies sont explorées. La première consiste, par modification de la paroi, à diminuer le coefficient de frottement moyen de la couche limite turbulente; ceci est obtenu par l’utilisation de parois comportant de petites rainures (appelées riblets ), disposées parallèlement à la vitesse amont, de section triangulaire et de hauteur inférieure à 0,1 mm; les gains de traînée de frottement obtenus varient entre 5 et 10 p. 100. La seconde voie consiste à maintenir, comme sur les planeurs, une couche limite laminaire sur une partie importante de la voilure, de la dérive et des empennages. Ceci peut être réalisé sur les avions à flèche modérée ( 淋 麗 200) par l’utilisation de profils laminaires adaptés au vol transsonique (laminarité naturelle), en revanche pour les avions à flèche plus élevée ( 淋 礪 200), la transition ne peut être évitée que par une aspiration à la paroi (laminarité contrôlée). Dans les deux cas, les gains de traînée de frottement sur la voilure sont évalués à environ 50 p. 100, soit un gain de traînée total de l’avion de 10 p. 100 à 15 p. 100 selon les surfaces «laminarisées». Ces gains sont très importants mais nécessitent des adaptations, voire des modifications, des technologies de fabrication, ainsi que la mise au point des systèmes particuliers de contrôle, de régulation, etc.
Aérodynamique des avions de transport supersoniques
La réduction des temps de vol sur les longs parcours est l’objectif du transport supersonique. Le seul avion de ce type actuellement en service commercial est le Concorde, et cela depuis 1975. D’autres projets actuellement à l’étude pourraient déboucher sur de nouveaux appareils au début du siècle prochain.
Pour minimiser la traînée en croisière supersonique, les voilures sont à forte flèche (bords d’attaque subsoniques), les profils ont de très faibles épaisseurs relatives (face=F0019 諒 4 p. 100), les formes avant et arrière du fuselage sont pointues et élancées; de plus, le C z de croisière est très faible (face=F0019 力 0,1). Malgré cela, les finesses sont nettement plus faibles que celles des avions subsoniques, puisque, pour Concorde, la finesse en croisière est voisine de 8, et une valeur de 11 est visée pour les projets futurs au même nombre de Mach de croisière (M 0 力 2).
Les niveaux de C z requis pour l’atterrissage et le décollage sont relativement faibles (face=F0019 力 de 0,6 à 0,8), néanmoins, pour atteindre ces niveaux de portance, pour ces ailes de faible allongement, il faut des incidences élevées conduisant à l’apparition d’écoulements tourbillonnaires à l’extrados qui augmentent la portance (portance tourbillonnaire), mais augmentent aussi fortement la traînée. Ainsi sur Concorde, à l’atterrissage, la portance tourbillonnaire représente 30 p. 100 de la portance totale et la finesse est d’environ 5. Un problème spécifique du vol à grande vitesse est l’échauffement cinétique, c’est-à-dire l’échauffement de la paroi dû au frottement de l’air. La température d’équilibre de la paroi est donnée par la loi T p = T 0 (1 + 0,18 M 20) où T 0 est la température ambiante et M 0 le mach de croisière. Ainsi à M 0 = 2 et Z = 15 km (T 0 = 217 K), T p = 375 K, soit 100 0C (fig. 37). En fait, une partie du flux de chaleur est rayonné, et les températures de paroi sont légèrement inférieures. L’échauffement cinétique limite le nombre de Mach de croisière, car l’utilisation d’alliages légers pour la structure ne permet pas de dépasser M 0 力 2,4.
Le problème majeur pour ces avions est cependant le «bang» supersonique dû aux variations brutales de pression engendrées par les ondes de choc attachées à l’avion en vol supersonique et qui se propagent jusqu’au sol. L’effet, au sol, de ces ondes de choc est plus important à la verticale de la trajectoire de l’avion, mais est encore sensible à des distances latérales d’environ 50 km. Ce «bang» interdit donc pratiquement le survol en supersonique des terres habitées, d’où la nécessité pour ces avions de posséder également de bonnes performanes à des nombres de Mach légèrement subsoniques (face=F0019 力 0,9).
Aérodynamique des avions militaires
Les avions militaires doivent effectuer différentes missions correspondant à des performances aérodynamiques également différentes. Pour les missions d’interception qui exigent d’excellentes capacités d’accélération, on recherchera le meilleur rapport poussée-poids et la plus faible traînée à faible incidence dans tout le domaine de vitesse et d’altitude. Pour la supériorité aérienne, les avions doivent être «manœuvrants» et «agiles», ce qui implique de forts C zmax , de grandes finesses à fort C z , ainsi que des gouvernes permettant le contrôle de l’appareil aux fortes incidences, voire au-delà du C zmax . Pour les missions de pénétration à basse altitude ou d’attaque au sol, l’avion ne doit pas être sensible aux rafales ou turbulences atmosphériques, afin d’assurer une bonne précision du tir; l’on cherchera à cet effet à minimiser la surface de voilure et la pente dC z /d 見 . Pour les missions stratégiques, l’avion doit avoir un rayon d’action élevé, d’où une finesse importante dans les conditions de croisière à haute altitude avec des charges externes. Enfin, pour les missions de reconnaissance ou de surveillance, l’avion doit être capable de vols de longues durées sans ravitaillement, d’où la recherche de faibles niveaux de traînée. Quelle que soit la mission, la portance maximale aux basses vitesses doit être élevée pour réduire les distances de décollage et d’atterrissage, ceci étant encore plus important pour les avions embarqués sur porte-avions. D’autres paramètres non aérodynamiques, tels que la discrétion électromagnétique ou infrarouge, peuvent influencer fortement les formes de l’avion (B-2, F-117). Si l’on excepte les missions stratégiques (Tupolev 160 et 22 M, B-52, B-1 B, B-2, Mirage IV) et les missions de surveillance (Awacs), la tendance actuelle est de définir des avions capables d’effectuer l’ensemble des autres missions. De ce fait, les voilures des avions militaires récents présentent généralement un bord d’attaque à double flèche, et l’allongement est voisin de 3, ce qui assure un bon compromis entre les exigences de finesse aux faibles incidences en supersonique et aux fortes incidences en subsonique.
En pratique, les manœuvres sont limitées non pas par le C z maximum, mais par le C z utilisable, c’est-à-dire, le C z pour lequel n’apparaissent pas encore de troubles aérodynamiques tels que le départ en roulis, l’autocabrage, etc., troubles dus essentiellement à l’éclatement des tourbillons présents sur ces voilures de faible allongement et à forte flèche. Pour accroître le C z utilisable, différents dispositifs sont utilisés pour augmenter la portance tourbillonnaire et retarder l’éclatement des tourbillons (fig. 38), ce sont essentiellement:
– les «strakes», petites surfaces portantes à forte flèche placées à l’emplanture de la voilure (F-16, F-18) et la prolongeant vers l’avant;
– les canards, petites ailes placées en amont et généralement au-dessus de la voilure principale (Rafale, E.F.A.).
Sur les avions récents, la finesse aux forts C z est améliorée par une cambrure de l’aile réalisée à l’aide de becs de bords d’attaque et, de volets de bords de fuite (F-16, F-18, F-111, Mirage 2000, Rafale, E.F.A.).
Deux concepts sont actuellement au stade expérimental, il s’agit de la poussée vectorielle et de la flèche inverse. La poussée vectorielle consiste à orienter le vecteur poussée du moteur, grâce à une tuyère à géométrie variable, pour générer une composante de sustentation s’ajoutant à la portance aérodynamique.
Une aile à flèche inverse (négative) possède à fort C z de meilleures caractéristiques aérodynamiques qu’une aile à flèche classique (positive). En effet, la répartition de portance en envergure permet d’obtenir de plus faibles traînées induites et une meilleure efficacité des ailerons. En revanche, les problèmes structuraux liés à la flèche inverse conduisent à des ailes plus lourdes. L’utilisation de matériaux composites permet de limiter cet inconvénient, et un avion expérimental, le X-29, utilise ce concept de flèche inverse.
L’utilisation de la flèche variable permet de conférer à l’avion de bonnes performances dans tout le domaine de vol; en revanche cette solution impose une augmentation de la masse de l’avion et une plus grande complexité des systèmes de commande et de contrôle.
L’emport de charges (bombes, missiles, réservoirs auxiliaires) conduit à une augmentation importante de la traînée et par conséquent à une diminution des performances de l’avion (accélération, rayon d’action, manœuvrabilité). Une optimisation de l’emplacement des charges ou l’utilisation de «containers» profilés permettent de réduire le supplément de traînée.
Aérodynamique des missiles
Pour les missiles stratégiques à longue portée (plusieurs milliers de kilomètres), la trajectoire est balistique, et ils n’ont pas à effectuer de manœuvres, sauf éventuellement en phase terminale. L’aérodynamique joue donc un rôle secondaire et n’intervient que pour la stabilité, de façon à maintenir l’engin sur sa trajectoire.
Pour les missiles tactiques de plus faible portée (quelques centaines de kilomètres au maximum), et qui évoluent à des nombres de Mach plus faibles (face=F0019 麗 6) et à des altitudes également plus faibles (face=F0019 麗 30 km), l’aérodynamique joue un rôle beaucoup plus important.
Ces missiles peuvent avoir des architectures différentes du fait de leur mission, du système de lancement, du système de guidage, etc. La portance du fuselage étant généralement insuffisante, plusieurs voilures (deux ou quatre) sont souvent nécessaires, mais, compte tenu des contraintes d’encombrement, ces voilures ont généralement des envergures et des allongements très faibles (de 0,3 à 4). Des gouvernes aérodynamiques, telles que les canards ou les empennages, placées en amont ou en aval du centre de gravité créent des moments aérodynamiques qui modifient l’attitude de l’engin (incidence, dérapage ou roulis) [fig. 39]. Lorsque le missile est tiré avec une faible vitesse initiale et/ou à haute altitude, la pression cinétique 福 V 2/2 étant faible, les efforts aérodynamiques sont insuffisants pour piloter le missile. Dans ce cas, le pilotage est réalisé soit par orientation du vecteur poussée du moteur, soit par des jets d’air comprimé ou d’autres gaz localisés à certains endroits du missile.
La traînée des missiles est également un paramètre important, puisqu’elle conditionne sa vitesse et sa portée. Pour minimiser la traînée de l’ogive, celle-ci est généralement pointue et de forme parabolique avec une longueur d’environ trois fois le diamètre du missile. La traînée de culot, qui peut représenter de 20 à 40 p. 100 de la traînée totale, est diminuée par un rétreint de la partie arrière réduisant la surface du culot et augmentant le niveau de la pression dans la zone décollée en aval du culot. Lorsque le missile comporte une tuyère, l’écoulement du culot est complexe, car il y a interaction entre le jet de la tuyère et l’écoulement extérieur. Ainsi, si la pression ambiante est inférieure à la pression du jet, ce qui se produit à haute altitude, le jet s’évase fortement et peut engendrer un décollement sur la partie arrière du fuselage, augmentant la traînée et réduisant l’efficacité des gouvernes.
Aérodynamique des véhicules spatiaux
Si l’on excepte les missiles balistiques, les véhicules spatiaux sont soit des capsules soit des navettes spatiales (navettes américaines ou soviétiques, projet Hermès). Le domaine de vol de ces véhicules est très étendu en nombre de Mach (0 諒 M 0 諒 30) et en altitude (0 諒 Z 諒 100 km). Outre les problèmes d’aérodynamique classique, des problèmes spécifiques liés aux forts nombres de Mach (aérodynamique hypersonique) et aux altitudes élevées (aérodynamique moléculaire) sont à résoudre pour ces véhicules. Pour les nombres de Mach élevés, des ondes de choc très intenses et enveloppantes se forment près de l’obstacle, la zone entre le choc et l’obstacle est appelée couche de choc. À travers l’onde de choc intense, l’entropie augmente fortement dans une zone, appelée couche d’entropie, qui se mélange à la couche limite et contribue également à la traînée.
À travers l’onde de choc, la température augmente considérablement, pouvant atteindre des valeurs supérieures à 6 000 K. À ces niveaux de température, les molécules d’oxygène et d’azote se dissocient en atomes, et le gaz s’ionise avec formation d’ions et d’électrons libres (plasma) qui perturbent la propagation des ondes (phénomène de blackout lors de la phase de rentrée). Ces fortes températures conduisent à des flux de chaleur à la paroi, maximaux au voisinage du nez, où ils peuvent atteindre plusieurs milliers de watts par mètre carré, nécessitant des protections thermiques très élaborées avec des matériaux ablatifs se «détruisant» en absorbant une partie de l’énergie thermique.
Aux altitudes élevées, l’air se raréfie, le libre parcours moyen des molécules (distance moyenne entre deux collisions successives des molécules) devient très grand, et le nombre de particules n par unité de volume (densité particulaire) diminue fortement. Dans ces conditions, l’air ne peut plus être considéré comme un «milieu continu», et les équations de l’aérodynamique classique sont mises en défaut; les molécules d’air se comportent comme des «projectiles» bombardant les parois en se réfléchissant ou en glissant sur celles-ci. Ainsi, pour un véhicule de 10 m de longueur, le régime moléculaire domine pour Z 閭 180 km; l’aérodynamique classique étant valable pour des altitudes Z 諒 100 km. Les effets visqueux sont plus importants relativement que pour l’aérodynamique aux plus faibles vitesses (interaction visqueuse importante), cela étant accentué lorsque des ondes de choc entrent en interaction avec la couche limite en l’épaississant encore davantage. Ces effets visqueux modifient de manière sensible le champ de pression sur les obstacles. Des théories simplifiées permettent cependant d’estimer correctement certains coefficients aérodynamiques. C’est le cas de la théorie de Newton, dans laquelle seules les particules «captées» par l’obstacle induisent des efforts (fig. 40). Cette théorie appliquée à une aile épaisse conduit à une pente dC z /d 見 ( 見 incidence) faible à l’origine et à une finesse maximale de 2,3 pour une incidence de 90 (sans tenir compte des effets visqueux); 90 p. 100 de la traînée provient du nez et du bord d’attaque de l’aile, ce qui est bien vérifié expérimentalement. La finesse est un paramètre essentiel pour les navettes spatiales, très faible pour les capsules habitées (face=F0019 麗 0,5) elle est voisine de 2 pour les navettes actuelles et permet d’obtenir un rayon d’action suffisant par rapport au plan de l’orbite (déport latéral) pour pouvoir atterrir sur un terrain prédéterminé avec possibilité de déroutement.
La rentrée dans l’atmosphère est une phase délicate, le «corridor» de rentrée étant relativement étroit et limité d’une part par la portance maximale du véhicule et d’autre part l’échauffement de la cellule. Les formes arrondies caractéristiques du nez et des bords d’attaque des ailes et de la dérive sont destinées à accroître la traînée, et donc la décélération, et à diminuer les flux thermiques. La finesse augmente continûment depuis une valeur 力 1 en début de rentrée jusqu’à une valeur de 力 3,5 en subsonique, valeur permettant de limiter la vitesse d’atterrissage et la longueur de piste nécessaire.
Aérodynamique des hélicoptères
La capacité des hélicoptères à décoller et à atterrir verticalement et de pouvoir rester immobiles (vol stationnaire) offre beaucoup d’avantages, et de telles machines sont apparues sensiblement en même temps que les avions, puisque les deux premiers hélicoptères «officiels» sont ceux de Louis Breguet en 1907, exception faite bien entendu des dessins de Léonard de Vinci.
L’accélération d’une masse d’air à l’aide d’une hélice ou d’un rotor d’une vitesse nulle à une vitesse V j procure une poussée (ou une traction) égale à T = q m V j , q m étant le débit en masse de l’air accéléré. La puissance à fournir est P i = (1/2) q m V 2j et l’efficacité peut être traduite par le rapport T/P i (poussée spécifique), qui est égal à 2/V j . Pour l’hélicoptère, cette poussée spécifique est plus élevée que pour d’autres systèmes, car la vitesse V j est relativement faible (face=F0019 力 20 m/s), si bien que le «rendement» de l’hélicoptère pour l’essor vertical est le plus élevé (fig. 41). En revanche, en vol de croisière l’hélicoptère a, de par son architecture, une finesse relativement faible (de 3 à 5), et par conséquent son efficacité énergétique est inférieure à celle des avions. Le rotor assure à la fois la portance (sustentation) et la propulsion, qui est obtenue par basculement vers l’amont de l’axe de rotation du rotor (fig. 42). La rotation du rotor engendre des efforts aérodynamiques sur les pales se décomposant en une force de portance et une force de traînée, cette dernière s’opposant à la rotation. Pour vaincre cet effort de traînée et maintenir une rotation du rotor, il faut fournir au rotor un couple moteur.
Ce couple moteur induit sur la cellule un couple opposé qui est contrebalancé par un rotor de queue. En vol d’avancement, la vitesse relative de l’air par rapport à la pale résulte de la combinaison de la vitesse de rotation 行 du rotor et de la vitesse d’avancement V a de l’appareil. Elle est égale, pour un profil de pale situé au rayon r , à V e = 行 r + V a sin 切 , soit V e = 行 R (r /R + 猪 sin 切 ), R étant le rayon du rotor, 猪 = V a/ 行 R k paramètre d’avancement de l’hélicoptère, et 切 la position azimutale de la pale. La pression cinétique relative correspondante (1/2) 福 V 2e n’est donc pas symétrique par rapport à la direction de déplacement de l’appareil avec une valeur supérieure du côté de la pale avançante (0 諒 切 諒 1800) par rapport au côté de la pale reculante (1800 諒 切 諒 3600). Pour supprimer le moment de roulis correspondant, les pales sont articulées au niveau du moyeu, et le mouvement de «battement» ainsi permis élimine l’effet de la dissymétrie; ce mouvement reste relativement faible en amplitude car les efforts centrifuges sont très nettement supérieurs aux efforts aérodynamiques. Une autre articulation permet des mouvements selon le plan de la pale contrant ainsi les effets dus à la fluctuation de la force de traînée.
En plus des articulations de battement et de traînée, une variation sinusoïdale du calage des pales et donc de l’incidence est imposée, au cours de la rotation (pas cyclique), autour d’une valeur moyenne (pas collectif), ce qui permet le contrôle de l’attitude de l’appareil en tangage et en roulis.
Ces variations de vitesse et d’incidence au cours de la rotation de la pale induisent des effets instationnaires d’autant plus importants que l’écoulement sur la pale est proche du décollement ou transsonique. Une autre particularité de l’hélicoptère concerne le sillage du rotor qui peut être schématisé par une nappe tourbillonnaire liée à chaque pale, s’enroulant de façon sensiblement hélicoïdale en vol stationnaire, la géométrie étant plus complexe en vol d’avancement. Ce sillage entre en interaction avec les autres éléments de l’appareil (fuselage, dérive...), et le sillage de chaque pale avec la suivante, créant des fluctuations des pressions qui sont une source de bruit et de fatigue structurale.
En vol stationnaire, il faut minimiser la puissance perdue par la traînée des pales (traînée de frottement et traînée due à l’allongement fini de la pale) et l’on utilise un vrillage de la pale pour obtenir une répartition optimale de portance en envergure et des profils possédant une bonne finesse dans les conditions de fonctionnement correspondantes (M 力 0,6 et C z 力 0,6).
En vol d’avancement, il faut diminuer la puissance perdue par les traînées des pales et de la cellule.
L’application du concept supercritique a permis d’améliorer sensiblement les performances des profils pour pale d’hélicoptère ces dernières années, d’où des gains significatifs sur la finesse des rotors, notamment aux vitesses d’avancement élevées. Par ailleurs de nouvelles formes d’extrémité de pale permettent également de réduire la traînée en pale avançante et de minimiser les interactions tourbillonnaires, et donc le bruit.
Les avions à décollage et atterrissage vertical (A.D.A.V.) ou court (A.D.A.C.)
L’augmentation importante des traînées du rotor et de la cellule avec la vitesse limite la vitesse maximale des hélicoptères à environ 300 km/h. Pour conserver les avantages de l’hélicoptère et pouvoir voler plus vite, plusieurs formules sont possibles.
Le «convertible» (V-22 Osprey ou le projet Eurofar) est un appareil comportant deux rotors basculants aux extrémités de l’aile. À l’atterrissage et au décollage, les axes des rotors sont verticaux et le fonctionnement est du type hélicoptère, le pilotage étant assuré sur les trois axes (roulis, tangage, lacet) par variation des pas collectif et cyclique des deux rotors. En vol d’avancement, les axes des rotors sont horizontaux et le fonctionnement est du type avion, les rotors, comme des hélices, fournissant la traction et la voilure assurant la portance.
D’autres formules privilégient davantage la croisière comme les formules à hélices carénées pivotantes où les formules utilisant la déflexion des jets des réacteurs (Harrier AV-8 B).
Les appareils à décollage et atterrissage court sont des avions possédant de fortes portances maximales aux basses vitesses obtenues grâce à un soufflage effectué au niveau des systèmes hypersustentateurs. Ce soufflage peut provenir des hélices (Breguet 941), des réacteurs (YC-14, YC-15, Q.S.R.A.) ou par un dispositif spécial (CV-7 A Buffalo). Le soufflage retarde l’apparition des décollements de couche limite sur les volets, induit un effet d’hypercirculation, et une partie de sa quantité de mouvement est également récupérée sous forme de force de portance. Ces trois effets combinés permettent d’obtenir des C z maximaux compris entre 6 et 9 alors que les C z maximaux des dispositifs classiques n’excèdent pas de 3,5 à 4 actuellement.
Aérodynamique interne
L’aérodynamique des divers constituants des moteurs aérobies que sont la prise d’air, le compresseur, la turbine et la tuyère pour les turboréacteurs conditionne le rendement du système propulsif et la traînée de l’ensemble de la configuration qu’ils propulsent (avions, missiles).
Aérodynamique des prises d’air
Le rôle de la prise d’air est de capter l’air pour alimenter la chambre de combustion. Elle transforme l’énergie cinétique de l’air capté en énergie potentielle, par ralentissement de l’écoulement. Les principaux paramètres utilisés pour les prises d’air sont le coefficient de débit 﨎 = A 0/A 1 (A 0 section du tube de courant capté à l’amont, A 1 section d’entrée), l’efficacité 兀 = P i2 /P i0 (P i2 : pression d’arrêt moyenne dans le plan d’entrée compresseur pour un turboréacteur ou à l’entrée de la chambre de combustion pour un statoréacteur; et P i0 : pression d’arrêt ambiante) [fig. 43]. Plusieurs critères sont par ailleurs utilisés pour qualifier la distorsion de l’écoulement dans le plan d’entrée du compresseur.
Pour les avions de transport subsoniques, les prises d’air sont de type Pitot et de formes sensiblement axisymétriques. Selon le régime du moteur, le coefficient de débit 﨎 peut être supérieur ou inférieur à 1. La traînée d’une prise d’air résulte des efforts de pression et de frottement qui s’exercent sur la paroi externe (traînée de carène), mais aussi d’un terme supplémentaire la résistance additive, résultante des efforts de pression sur les faces du tube de courant capté entre l’infini amont et le plan d’entrée. Un dessin soigné du bord d’attaque de la prise d’air permet d’obtenir des efficacités très proches de l’unité et de minimiser la traînée de carène.
Pour les véhicules supersoniques, il faut ralentir considérablement l’écoulement, et l’utilisation de prises d’air Pitot conduirait à la formation d’ondes de choc droites intenses devant la prise d’air et à de faibles efficacités. On utilise donc généralement des prises d’air à compression supersonique externe bidimensionnelles ou axisymétriques dans lesquelles l’écoulement est ralenti à travers un choc ou une succession de chocs obliques générés par des rampes. Le fonctionnement de la prise d’air est représenté par l’évolution de l’efficacité en fonction du coefficient de débit (caractéristique). Le régime critique est le régime optimal de fonctionnement, il procure une bonne efficacité et une marge de sécurité vis-à-vis du pompage. Pour accroître le domaine de bon fonctionnement de la prise d’air, celle-ci est souvent dotée de parties mobiles (rampes ou souris) réglables en fonction des conditions de vol et du régime moteur. L’efficacité de la prise d’air est également améliorée en aspirant la couche limite qui se développe le long des rampes de compression à travers un «piège interne» dont le débit est réinjecté au niveau de la tuyère (fig. 44). Le piège interne permet également de retarder l’apparition du pompage. Les efficacités maximales obtenues sont voisines de 0,95 par un nombre de Mach de croisière de 2.
Aérodynamique des tuyères et des arrière-corps
Le rôle de la tuyère est de poursuivre la détente de la turbine et de transformer l’énergie potentielle en énergie cinétique. Cette transformation procure une poussée (le reste de la poussée provenant du moteur et de la prise d’air). L’arrière-corps est la partie externe de la tuyère. Pour les avions subsoniques, les tuyères sont convergentes; les flux primaire et secondaire peuvent être séparés, confluents ou mélangés.
Pour les avions supersoniques, les tuyères sont convergentes-divergentes; les débits provenant du piège à couche limite et des circuits de refroidissement sont réinjectés généralement au voisinage du col de la tuyère principale. Les sections du col et de sortie sont réglables de manière à assurer un bon fonctionnement de la tuyère dans tout le domaine de vol (subsonique, supersonique avec et sans réchauffe).
Aérodynamique des compresseurs et des turbines
Le compresseur assure un débit au point fixe (V 0 = 0), procure de l’énergie cinétique à l’air qui le traverse et transforme cette énergie cinétique en pression. À l’inverse, la turbine prélève dans le fluide de l’énergie de pression, qu’elle transforme en énergie cinétique, puis en puissance sur l’arbre. On appelle corps un ensemble compresseur-turbine accouplés sur un même arbre et tournant donc à la même vitesse. Un turboréacteur peut être mono-, double ou triple corps. Les aubes sont constituées par un empilage de profils aérodynamiques dont les caractéristiques géométriques évoluent avec le rayon (corde, épaisseur, calage, etc.). Une grille est un ensemble d’aubes identiques disposées sur un même rayon à des intervalles angulaires 2 神/n égaux (n : nombre d’aubes). Une grille est définie par divers paramètres tels que le rapport de moyeu R i/R e (rapport des rayons minimum et maximum), le rapport des sections S 2/S 1 de passage du fluide entre la sortie et l’entrée de la grille, le pas relatif t /c (t : distance qui sépare deux profils au même rayon; c : corde des profils à ce rayon) [fig. 45]. Le rôle d’une grille, fixe ou mobile, de compression ou de détente, est de modifier la direction et le module du vecteur vitesse. La déviation est surtout liée aux caractéristiques des profils (cambrure, calage) et au pas relatif de la grille. La variation du module de la vitesse est liée au rapport des sections de passage du fluide entre l’entrée et la sortie de la grille; ces sections diminuent pour une compression (S 2 礪 S 1) et augmentent pour une détente (S 2 礪 S 1). Dans les études de grille, on est amené à considérer trois vitesses: la vitesse absolue ふ, la vitesse relative ぶ et la vitesse d’entraînement ぴ(U = 行 r ) liées par la relation ふ = ぴ + ぶ.
Dans un compresseur axial, les évolutions des vecteurs vitesse entre l’entrée et la sortie des grilles mobiles ou fixes sont tracées dans des diagrammes appelés triangles des vitesses, qui évoluent en fonction du rayon considéré (fig. 46). Le taux de compression est lié à l’augmentation de la température provenant du ralentissement de l’écoulement dans la grille mobile (W 2 麗 W 1), dans la grille fixe (V 3 麗 V 2) et de l’effet centrifuge (U 1 麗 U 2). La variation de température statique dans un étage ne dépasse généralement pas 15 p. 100 en valeur relative ( T/T 諒 0,15). La «charge» de l’étage est la variation d’enthalpie correspondante H = C p T (C p, chaleur massique à pression constante). Le rôle des profils est d’assurer les déviations de l’écoulement avec le moins de pertes possible, ces pertes étant exprimées à l’aide d’un coefficient 諸 = (P i1 漣 P i2 )/(P i1 漣 p 1) (P i pression d’arrêt, p pression statique) équivalent au C x des profils isolés.
On trace l’évolution de ce coefficient en fonction de l’angle d’entrée 廓 1 de la grille, ce qui correspond aux courbes C x ( 見 ) des profils isolés. La plage de fonctionnement avec de faibles pertes est beaucoup plus réduite que pour un profil isolé, du fait des interactions avec les profils voisins. Cette plage diminue lorsque le nombre de Mach amont augmente par suite de l’apparition sur les profils d’ondes de choc.
En plus des pertes dues aux couches limites et aux ondes de choc, une autre source de pertes est l’existence de jeux entre les parties mobiles et les parties fixes. Ces jeux permettent des écoulements entre l’intrados et l’extrados de la roue mobile et du stator, appelés écoulements secondaires. De plus, les sillages d’une grille entrent en interaction avec les aubes de la grille suivante et la présence d’organes mobiles rend l’écoulement instationnaire.
Les turbines axiales sont constituées d’étages successifs comprenant une grille fixe suivie d’une grille mobile; la grille fixe transforme la pression du fluide en vitesse et la grille mobile transforme cette vitesse en travail recueilli sur l’arbre de la roue. L’évolution des vitesses axiales est obtenue par la loi des sections de passage du fluide, qui augmentent progressivement. La variation relative de température dans un étage T /T est comme pour les compresseurs comprise entre 0,08 et 0,15. Cependant, comme la température est beaucoup plus élevée que dans le compresseur le T , et, par suite, la variation d’enthalpie H est environ cinq à six fois plus grande que pour le compresseur et un étage de turbine peut donc entraîner cinq à six étages de compresseur (maximum 力 9). Pour les profils les déviations sont très élevées (face=F0019 力 de 90 à 1200), les canaux interaubes sont convergents; les profils sont beaucoup plus épais que pour les compresseurs. Les premiers étages de turbine, placés juste en aval de la chambre de combustion fonctionnent à des températures très élevées. Les aubes sont refroidies par de l’air prélevé au niveau du compresseur, et qui circule à l’intérieur des aubes à travers de petits canaux ou des cavités, et est évacué par des trous disposés sur la surface de l’aube, permettant ainsi la création d’un film d’air «froid» limitant la température.
Aérodynamique des hélices
L’hélice fournit une traction orientée selon son axe de rotation. Le pas de l’hélice au rayon r est t = 2 神r tan , étant l’angle entre la corde du profil et la vitesse de rotation U (calage). Les hélices classiques comportant généralement de deux à quatre pales, les pas relatifs t/c (c : corde des profils) sont élevés, et les profils peuvent être considérés comme des profils «isolés», sauf au voisinage du moyeu ou des effets de «grille» peuvent apparaître. La force aérodynamique s’exerçant sur un élément de pale peut être décomposée en une composante selon la direction de l’axe (traction) et une composante perpendiculaire provoquant un couple.
Les performances des hélices sont traduites par les évolutions des coefficients de traction 精 = T /( 福 0N 2D 4) de couple C M = C ( 福 0N 2D 5) et de puissance X = P / 福 0N 3D 5) en fonction du paramètre d’avancement 塚 = V 0/ND . Dans ces formules, N est la fréquence angulaire égale à 行 /2 神, D le diamètre extérieur de l’hélice et 福 0 la masse volumique de l’air. Le rendement, 兀 = ( 精 /X ) 塚 , passe par un maximum pour une valeur de 塚 , ce qui conduit à l’utilisation d’hélices à pas variable (r tan variable) pour adapter l’hélice en fonction des conditions de vol. Les profils doivent posséder de bonnes performances aux forts C z (finesse élevée) pour procurer à l’hélice de fortes valeurs de traction au décollage et en montée. Les hélices possèdent de bonnes performances aux faibles vitesses d’avancement ( 兀 力 de 0,80 à 0,85), par contre, pour des nombres de Mach de croisière supérieurs à 0,5, leurs performances chutent rapidement du fait de l’apparition d’ondes de choc sur les pales. Récemment de nouvelles hélices ont été définies pour des nombres de Mach de croisière plus élevés (de 0,7 à 0,8). Ces hélices transsoniques ou prop fan sont caractérisées par des pales en flèche, la flèche étant, comme sur les ailes, destinée à retarder l’apparition des problèmes transsoniques et un nombre de pales élevé (de 8 à 12) [fig. 47].
Aérodynamique des éoliennes
Les éoliennes captent l’énergie cinétique du vent pour la transformer en énergie mécanique utilisée directement ou transformée en énergie électrique. Le fonctionnement des éoliennes à axe horizontal est voisin de celui des hélices, la différence provenant du fait que, contrairement à l’hélice, l’éolienne ralentit l’écoulement d’air qui la traverse, la vitesse à l’aval étant égale à un tiers de la vitesse du vent pour un fonctionnement optimal. La puissance maximale correspondante est égale à P max = 8/27 福 S V 3 (S : surface du disque de l’hélice; V : vitesse du vent). En pratique, la puissance récupérée ne dépasse pas en général de 60 à 70 p. 100 de la puissance maximale donnée par la formule de Betz précédente, du fait des pertes aérodynamiques et mécaniques. Les profils utilisés pour les pales varient selon le type de machine. Pour les moulins à vent, les ailes étant constituées par une charpente de bois recouverte de toile, les qualités aérodynamiques (finesse) n’étaient pas très grandes; il en est de même des éoliennes lentes dont les profils sont très minces et cambrés. Pour les éoliennes rapides, et notamment sur les machines récentes, on utilise des profils possédant une bonne finesse (C z /C x ) pour améliorer le rendement. Les profils fonctionnent à faible nombre de Reynolds (R e = 福 Vl / 猪 ) généralement inférieurs à 500 000, les couches limites sont épaisses, et des décollements apparaissent soit au niveau de la transition de la couche limite, soit au bord de fuite.
Aérodynamique des véhicules terrestres
L’aérodynamique des voitures, des camions et des motocycles prend d’autant plus d’importance que les vitesses augmentent et que se posent avec acuité les problèmes d’économie d’énergie. La puissance perdue pour vaincre la résistance à l’avancement P = (1/2)( 福 S v 3C x ) sera d’autant plus faible que le coefficient de traînée C x du véhicule sera petit. La plupart des voitures actuelles ont des C x de l’ordre de 0,3 à 0,4 (le C x étant calculé avec la surface frontale comme surface de référence), mais des valeurs beaucoup plus faibles (de 0,15 à 0,2) sont atteintes sur des prototypes (véhicules Orphée, Vesta ou Ève de Renault). La traînée de pression est de loin le terme le plus important; les parties du véhicule contribuant le plus à cette traînée sont les parties situées en amont du maître couple, où règnent des surpressions (avant, pare-brise) et les parties situées en aval du maître couple où règnent des dépressions (lunette arrière, arrière du véhicule) [fig. 48]. La structure de l’écoulement sur la partie arrière du véhicule, qui conditionne la distribution des pressions, et donc la traînée associée, est extrêmement complexe, avec des décollements s’organisant en tourbillons qui interagissent avec d’autres tourbillons, issus de l’avant (montants de pare-brise).
La portance du véhicule ainsi que la répartition de cette portance sur les quatre roues sont également des paramètres importants. La voiture assimilable à une aile de très faible allongement engendre une portance aérodynamique, qui augmente avec la vitesse F z = (1/2)( 福 S V 2 C z ) et qui provoque une diminution de l’adhérence (délestage). Le coefficient de portance C z dépend bien entendu de la forme de la carrosserie, mais aussi de la forme du plancher. D’une manière générale, on essaye d’obtenir des dépressions sous le plancher, de façon à limiter l’augmentation de la portance de la voiture. Lorsque cette portance est trop élevée cependant, notamment pour les voitures de compétition, l’on rajoute des surfaces déportantes (ailerons) à l’avant et à l’arrière pour augmenter les appuis sur les roues. La présence d’un vent latéral crée un effet de dérapage modifiant les caractéristiques aérodynamiques C z et C x mais surtout induit une force latérale F y et un moment de lacet N nuisibles à la tenue de route du véhicule.
Pour les véhicules industriels (camions, semi-remorques), les problèmes aérodynamiques sont voisins avec encore une importance plus grande pour la traînée et donc la consommation. En effet, à titre d’exemple, la consommation moyenne d’un véhicule de 38 t est due pour 20 p. 100 à sa traînée aérodynamique pour une vitesse de 80 km/h, mais ce chiffre passe à 40 p. 100 pour une vitesse de 90 km/h. Les formes avant et arrière, la géométrie du plancher, l’espace entre la cabine et la remorque sont les principaux éléments contribuant à la traînée.
Pour les motocycles, les formes aérodynamiques des carénages doivent permettre de protéger le conducteur du vent et des projections, de réduire la traînée de la machine, de minimiser les effets du vent latéral et de réduire la portance de la roue avant, afin de conserver une bonne adhérence à vitesse élevée.
Comme pour les véhicules routiers, l’augmentation de la vitesse des trains rend plus importants les problèmes aérodynamiques. Ces problèmes concernent bien entendu la résistance à l’avancement, mais aussi les variations de pression liées au croisement des trains ou à la circulation des trains dans les tunnels.
Pour un train roulant à 300 km/h, environ 90 p. 100 de la résistance totale provient de la traînée aérodynamique. Les principales sources de traînée aérodynamique sont les parties avant et arrière, l’espacement entre les voitures, l’état de surface (rugosités dues à la présence des vitres, des portières...), la forme du plancher sous les voitures (appendices, bogies...). La forme élancée de la partie avant du T.G.V. possède une traînée cinq fois plus faible que les formes avant des anciennes locomotives des séries BB ou CC. Cette forme avant conditionne également le champ de pression (fig. 49) induit par le déplacement du train et qui comporte à l’amont une zone de surpressions élevées suivie, au niveau du maître couple, d’une zone de dépression. Ces variations de pression, accentuées encore par la présence d’un tunnel où le croisement de deux trains, posent des problèmes mécaniques (tenue des vitres à l’avant) et de confort (bruit, niveau de pression interne) qui peuvent être réduits par un dessin soigné de la partie avant. Les bruits d’origine aérodynamique augmentant beaucoup plus rapidement avec la vitesse que les bruits de roulement, les formes extérieures doivent être le plus «lisses» possible pour éviter les décollements de couche limite, les formations de tourbillons qui sont source de bruit.
Aérodynamique des bateaux à voiles
L’aérodynamique des bateaux à voiles ne peut pas être dissociée de l’hydrodynamique, puisque l’équilibre du bateau est obtenu du fait de l’existence de forces hydrodynamiques sur la coque et sur la quille. Les efforts aérodynamiques sur la ou les voiles sont dus au «vent apparent» résultant de la combinaison du vent réel et de la vitesse du bateau. La force aérodynamique ainsi créée se projette en une composante propulsive selon la direction de la vitesse du bateau et en une composante perpendiculaire à la précédente. Ces efforts et les moments qui en résultent sont équilibrés par les forces et les moments hydrodynamiques, l’équilibre étant obtenu pour une certaine attitude de bateau (dérive, gîte). Les forces aérodynamiques dépendent de nombreux paramètres tels que la surface, la forme en plan de la voile, les formes des profils et du mât, la nature du tissu (porosité), les interactions entre les différentes voiles et bien entendu de l’incidence et du nombre de Reynolds. Les différences essentielles par rapport aux autres types de voilure proviennent de l’utilisation de profils très minces et d’un fonctionnement à faible nombre de Reynolds. Pour des incidences différentes de l’incidence d’adaptation correspondant à une vitesse tangente au squelette du bord d’attaque, des décollements apparaissent à l’extrados ou à l’intrados de ces profils leur conférant des performances médiocres (C z max, finesse) pour des nombres de Reynolds supérieurs à 黎 500 000; cependant, aux faibles nombres de Reynolds inférieurs à 500 000 correspondant au reynolds de fonctionnement des voiles des petits bateaux par vent faible, les performances de ces profils sont supérieures à celles des profils épais et, de plus, elles sont moins sensibles aux variations du nombre de Reynolds. L’utilisation de mâts profilés permet d’étendre la plage d’incidence de bon fonctionnement de ces profils. Les formes des voiles influencent également la finesse (forme en plan, allongement, effilement, vrillage). Pour les voiles triangulaires couramment utilisées et qui limitent le couple de gîte, les coefficients de portance sont les plus élevés en extrémité, dans une région où le nombre de Reynolds est le plus faible; il existe donc fréquemment une zone décollée qui peut être réduite par une cambrure plus accentuée de la voile. Les formes elliptiques ou rectangulaires qui procurent de meilleures finesses sont utilisées pour des «voiles» rigides conçues pour les bateaux pouvant accepter des couples de gîte plus importants (catamarans, hydrofoils). Les effets de la porosité des voiles sont surtout sensibles lorsque la différence de pression entre l’extrados et l’intrados est importante, c’est-à-dire pour des vitesses de vent élevées et de forts coefficients de portance, et se traduisent par une baisse de la finesse. Les finesses maximales des voiles triangulaires classiques varient entre 4 et 6 et les coefficients de portance maximale varient entre 1,2 à 1,6 selon la cambrure. L’utilisation de plusieurs voiles conduit à des interactions qui sont (lorsque les réglages sont corrects) favorables, permettant d’obtenir une portance totale supérieure à la somme des portances des deux voiles isolées.
Dans les conditions les plus favorables (V apparent perpendiculaire au vent réel), le rapport de la vitesse du bateau à la vitesse du vent ne peut dépasser 2 pour un petit monocoque ayant une finesse de voile de 6, et, même si la finesse était portée à 18, ce rapport ne serait que d’environ 2,5. L’obtention de rapports plus élevés nécessite des architectures différentes permettant d’utiliser de plus grandes forces aérodynamiques telles que les multicoques.
Aérodynamique des bâtiments
Les bâtiments et ouvrages d’art doivent être dimensionnés pour résister aux vitesses maximales du vent prévisibles à leur emplacement. Ces vitesses peuvent atteindre 150 à 200 km/h lors de tempêtes ou de violents orages et même davantage lors de passages de cyclones. Pour ces vitesses élevées, la pression cinétique (1/2)( 福 V 2) devient importante, ainsi que les efforts aérodynamiques. Pour les édifices de grande hauteur, les différences de pression cinétique entre la base et le sommet doivent être prises en compte pour le calcul de la répartition des efforts aérodynamiques. Cette différence de pression cinétique (1/2)( 福 V 2) est due à la présence de la couche limite terrestre dont la hauteur varie entre 300 et 500 m selon qu’il s’agit d’un site en rase campagne ou du centre d’une ville. Il en résulte une position du centre de poussée située au-dessus de la mi-hauteur et des couples de renversements élevés. Le profilage des bâtiments selon la direction des vents dominants permet de réduire les coefficients de traînée et par conséquent les efforts aérodynamiques.
À l’arrière des ouvrages mal profilés (cheminées, tours de refroidissement, bâtiments, ponts...) se développe un sillage constitué de tourbillons alternés dont la fréquence d’échappement augmente avec le nombre de Reynolds. Cette fréquence est caractérisée par le nombre de Strouhal Sr = fh /V (f : fréquence des tourbillons; h : épaisseur de l’obstacle; V : vitesse du vent). Ces tourbillons engendrent des fluctuations de la pression à la surface du corps à la fréquence d’échappement qui peuvent provoquer des oscillations de la structure si cette fréquence est voisine de la fréquence naturelle (phénomène de résonance). Des oscillations d’amplitude considérable peuvent ainsi être générées par des forces aérodynamiques relativement petites pouvant conduire à la destruction de l’édifice comme ce fut le cas pour le pont de Tacoma, aux États-Unis (fig. 50).
aérodynamique [ aerodinamik ] n. f. et adj.
• 1836; de aéro- et dynamique
1 ♦ Partie de la physique qui étudie les phénomènes accompagnant tout mouvement relatif entre un corps et l'air où il baigne. Aérodynamique théorique, expérimentale. Spécialiste de l'aérodynamique (AÉRODYNAMICIEN, IENNE n. ).
2 ♦ Adj. (1891) Relatif à l'aérodynamique et à ses études. Laboratoire, soufflerie aérodynamique.
♢ Conforme aux lois de l'aérodynamique. Profil aérodynamique, conçu pour améliorer la pénétration dans l'air (⇒ portance, traînée) . Frein aérodynamique. ⇒ aérofrein. Autom. Carrosserie, lignes aérodynamiques, profilées.
● aérodynamique adjectif Qui se rapporte à l'influence de l'air sur un corps en mouvement. Qui suit les lois de l'aérodynamique. ● aérodynamique (difficultés) adjectif Sens et emploi Le sens « qui est spécialement conçu pour offrir peu de résistance à l'air » est aujourd'hui admis : carrosserie aérodynamique. Remarque Cet emploi a été longtemps critiqué (le sens « qui utilise la force de l'air » était considéré comme seul correct). ● aérodynamique nom féminin Science qui étudie les phénomènes accompagnant tout mouvement relatif entre un corps et l'air qui l'entoure. (Le corps peut être fixe dans l'air en mouvement [écoulement autour d'un bâtiment soumis à l'action du vent] ou se déplacer dans l'air immobile [projectile, automobile, avion, etc.].) Ensemble des caractéristiques aérodynamiques d'un véhicule.
aérodynamique
n. f. et adj.
rI./r n. f. Science des phénomènes physiques liés au déplacement des corps solides dans l'atmosphère.
rII./r adj.
d1./d Relatif à cette science.
d2./d Caréné de façon à opposer à l'air une résistance minimale. Carrosserie de voiture aérodynamique.
⇒AÉRODYNAMIQUE, adj. et subst. fém.
PHYSIQUE
I.— Adjectif
A.— Qui est relatif aux lois du déplacement des corps dans l'air :
• 1. La vitesse propre, appelée aussi vitesse aérodynamique, est la vitesse de l'aéronef par rapport à l'air.
A.-B. DUVAL, L. HÉBRARD, Traité pratique de navigation aérienne, 1928, p. 50.
• 2. ... biplans et multiplans (...). Très mauvais rendement aérodynamique à cause de l'interaction du haubannage sur les ailes et des ailes entre elles.
J. GUILLEMIN, Précis de construction, calcul et essai des avions et hydravions, 1929, pp. 86-87.
• 3. [les] boques d'hydravions (...) [ont] leurs formes (...) déterminées par des conditions hydrodynamiques et aérodynamiques.
J. GUILLEMIN, Précis de construction, calcul et essai des avions et hydravions, 1929 p. 94.
• 4. Bien que l'aile soit la partie la plus importante de l'avion, tout au moins en ce qui concerne la portance, les autres éléments doivent être étudiés du point de vue aérodynamique, ne serait-ce que pour connaître leur traînée, leur influence sur la stabilité générale ou les répercussions que peuvent avoir les différentes interactions qui existent entre eux.
J. LACHNITT, L'Aérodynamique, coll. « Que sais-je? », 1965, p. 99.
Rem. Syntagmes : calculs, coefficients, conditions, échauffement, point de vue, rendement, vibrations, vitesse, etc. aérodynamique(s).
B.— [En parlant d'un obj. : avion, autom., train] Dont la forme est calculée de manière à offrir le minimum de résistance à l'air :
• 5. ... un fuselage [d'avion] ne présente pas (...), une surface extérieure suffisamment régulière et aérodynamique (...), [et] on englobe le fuselage dans un « carénage ».
J. GUILLEMIN, Précis de construction, calcul et essai des avions et hydravions, 1929, p. 161.
• 6. Équipement électrique pour bicyclette, comprenant : 1 dynamo, (...), 1 phare aérodynamique ...
Magasin du Louvre, Catalogue de jouets, 1937.
• 7. L'Iguanodon eût pu facilement déguster une douzaine de paniers d'huîtres au balcon d'un sixième étage. Après quoi il eût culbuté la maison comme on plie sa serviette et retourné trois tramways d'un coup de queue, histoire de dépenser un peu de phosphore. Nous avons beau être habitués aux trains « aérodynamiques » et aux immeubles de trente étages : ces monstres, qui poussaient comme des arbres au lieu de naître des cerveaux, ces bêtes de plusieurs tonnes descendent au fond de l'émotion et secouent fortement nos vieilles peurs éparses...
L.-P. FARGUE, Le Piéton de Paris, 1939, p. 127.
• 8. Les effets de l'écoulement de l'air autour des corps en mouvement ne se font pas sentir qu'en aviation (...) Un exemple récent vient d'en être donné dernièrement par le record de vitesse sur rail de la locomotive CC de la SNCF portée sur la ligne électrifiée Paris-Dijon à 340 km/h. Une telle performance n'a pu être obtenue que par une étude soignée du profil aérodynamique de la motrice dessinée pour offrir le moins de résistance au vent.
J. LACHNITT, L'Aérodynamique, coll. « Que sais-je? », 1965, p. 115.
Rem. Dans l'ex. suiv. aérodynamique est appliqué p. méton. au mot époque, et signifie « qui fait une large place aux considérations d'aérodynamique » :
• 9. « L'époque [notre époque] est aérodynamique et scientifique, ne l'oublions pas. »
L'Œuvre, 18 janv. 1937, p. 2, col. 1.
II.— Subst. fém.
A.— Vieilli. Partie de la physique qui étudie les lois du mouvement des fluides élastiques :
• 10. Je traiterai ici spécialement de l'aérostatique et de l'aérodynamique, c'est-à-dire des propriétés naturelles de l'air en repos et en mouvement.
HUREAU DE VILLENEUVE, L'Aéronaute, janv. 1871, p. 5 (GUILB. Aviat. 1965).
B.— En gén.
1. Partie de la physique qui étudie les lois du déplacement relatif d'un corps et de l'air environnant (déplacement de l'air qui s'écoule dans ou autour d'un corps, déplacement d'un corps dans un air aux caractéristiques variables) :
• 11. Il serait absurde et sans intérêt, pour représenter la pression du vent en aérodynamique, de vouloir utiliser un modèle mécanique, qui reproduirait chaque trajectoire moléculaire. Le savant s'occupe du résultat d'ensemble, qui est une réalité aussi authentique et bien plus intéressante que le mouvement de chaque molécule.
R. RUYER, Esquisse d'une philosophie de la structure, 1930, p. 241.
• 12. Les écoulements hypersoniques (...). Il est bien évident qu'à de telles vitesses les propriétés des écoulements de fluides sont très différentes de ce qu'elles sont aux vitesses supersoniques, et cela a ouvert un nouveau champ de recherches, l'aérodynamique hypersonique, sur lequel on sait encore fort peu de choses du fait de la rareté des résultats expérimentaux.
J. LACHNITT, L'Aérodynamique, coll. « Que sais-je? », 1965, p. 75.
2. En partic., TECHNOL. (aviat., autom., ch. de fer). Étude des rapports entre la forme et la position des engins et la pression de l'air dans lequel ils se déplacent; étude de ces rapports envisagée du point de vue de l'optimisation des engins :
• 13. ..., si (...) [la] permanence [de la forme] n'est pas assurée, il est (...) inutile de faire des études pour donner à l'enveloppe [du dirigeable] un profil irréprochable au point de vue de l'aérodynamique.
L. MARCHIS, Leçons sur la navigation aérienne, 1904, p. 593.
• 14. ... l'importance de l'aérodynamique [a] familiarisé l'œil moderne avec les courbes coniques en particulier : ellipses, hyperboles, paraboles... Un observateur attentif constatera quel est leur empire sur l'art d'aujourd'hui et ses arrangements, depuis le tableau jusqu'au meuble ou à la céramique; il mesurera combien elles tendent à remplacer les constructions planes basées surtout sur l'angle et le cercle, ces dominantes d'hier.
R. HUYGHE, Dialogue avec le visible, 1955, pp. 171-172.
Prononc. — 1. Forme phon. :[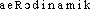
]. DUB. transcrit le préf. avec [o] fermé : 
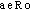-. Enq. :/
/. 2. Dér. et composés : aérodynamicien (cf. Lar. encyclop.), aérodynamisation, aérodynamisme, aérodynamiste.
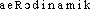]. DUB. transcrit le préf. avec [o] fermé : 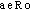-. Enq. ://. 2. Dér. et composés : aérodynamicien (cf. Lar. encyclop.), aérodynamisation, aérodynamisme, aérodynamiste.Étymol. ET HIST. — 1. Subst., 1836 phys. (RAYMOND, Suppl. au dict. de l'Ac. : Aérodynamique. Partie de la physique qui s'occupe des phénomènes dépendant de la pression atmosphérique); 2. adj., 1891 « qui a trait à l'aérodynamique » (l'Aéronaute, août 1891, p. 176 ds GUILB. Aviat. 1965, p. 407 : Recherches expérimentales aérodynamiques et données d'expérience par S. P. Lengley); 1929 (THÉRIVE, Querelles de langage, p. 167 ds QUEM. t. 1 1959); 1re moitié XXe s. autom. : lignes aérodynamiques (ds Fr. mod., VII, 15).
Composé de l'élément préf. aéro- et de dynamique.
STAT. — Fréq. abs. litt. :3.
BBG. — BÉL. 1957. — CHESN. 1857. — DELC. t. 1 1926. — GALIANA Astronaut. 1963. — GALIANA Déc. sc. 1968. — GALL. 1955, p. 123; pp. 139-141; p. 150, 204. — GUERBER 1967. — GUILB. Aviat. 1965. — HANSE 1949. — HÖFLER (M.). Une Source négligée de Landais et des Compléments au Dictionnaire de l'Académie française. Fr. mod. 1969, t. 37, p. 36. — LITTRÉ-ROBIN 1865. — SPITZER (L.). Néologismes. Aérodynamique. Total. Fr. mod. 1939, t. 7, pp. 15-19. — SPITZER (L.). Aérodynamique. Fr. mod. 1939, t. 7, p. 263. — THOMAS 1956. — UV.-CHAPMAN 1956.
aérodynamique [aeʀodinamik] n. f. et adj.
ÉTYM. 1842; de aéro-, et dynamique.
❖
———
I N. f. Partie de la physique qui étudie les phénomènes accompagnant tout mouvement relatif entre un corps et l'air où il baigne. || Aérodynamique théorique, expérimentale (→ Aérotechnique).
➪ tableau Noms de sciences et d'activités à caractère scientifique.
———
II Adj.
1 (1852, in D. D. L.). Sc. Relatif à l'aérodynamique et à ses études. || Laboratoire, soufflerie aérodynamique.
2 Cour. Conforme aux lois de l'aérodynamique. || Profil aérodynamique, conçu pour réduire le plus possible la résistance de l'air. || Frein aérodynamique (ou aérofrein). || Carrosserie d'automobile aérodynamique (⇒ aussi Becquet). || Lignes aérodynamiques, profilées.
1 Nous avons beau être habitués aux trains « aérodynamiques » et aux immeubles de trente étages : ces monstres, qui poussaient comme des arbres au lieu de naître des cerveaux, ces bêtes de plusieurs tonnes descendent au fond de l'émotion et secouent fortement nos vieilles peurs éparses (…)
Léon-Paul Fargue, le Piéton de Paris, p. 127.
REM. Le terme, dans son sens courant, a été refusé par certains puristes.
2 Ce terme (aérodynamique) ne veut absolument rien dire, et il est d'un pédantisme effarant (…) Cela n'empêchera pas le mot de faire, j'en suis sûr, une brillante carrière.
A. Thérive, Querelles de langage, t. III, p. 167-168.
❖
DÉR. et COMP. Aérodynamicien, aérodynamisme. Magnétoaérodynamique.
Encyclopédie Universelle. 2012.