- ГРУППА
-
- множество, на к-ром определена операция, наз. умножением и удовлетворяющая спец. условиям (групповым аксиомам): в Г. существует единичный элемент; для каждого элемента Г. существует обратный; операция умножения ассоциативна. Понятие Г. возникло как обобщение при рассмотрении конкретных групп преобразований (взаимно однозначных отображений разл. множеств на себя). Для преобразований роль умножения играет композиция преобразований, т. е. последоват. выполнение сначала одного из них, а потом второго. Такая операция по определению ассоциативна. Роль единицы играет тождественное преобразование. Любую Г. можно реализовать как Г. преобразований, сохранив при этом внутр. алгебраич. структуру.
Понятие Г. зародилось в кон. 18 - нач. 19 вв. независимо в трёх областях математики: в теории алгебраич. ур-ний [Ж. Лагранж (J. Lagrange), A. Вандермонд (A. Vandermonde), H. Абель (N. Abel), Э. Галуа (E. Galois)], геометрии [А. Мёбиус (A. Mobius), А. Кэли (A. Cayley)] и теории чисел [Л. Эйлер (L. Euler), К. Гаусс (С. Gauss)]. B законченном виде понятие Г. оформилось в кон. 19 - нач. 20 вв. [К. Жордан (С. Jordan), Ф. Клейн (F. Klein), C. Ли (S. Lie), Г. Вейль (H. Weyl)].
Б. ч. приложений теории Г. связана с тем, что в терминах Г. естественно выражается свойство симметрии той или иной физ. системы или её матем. модели (напр., геом. фигуры). Система обладает симметрией, если её свойства остаются инвариантными (неизменными) при нек-ром преобразовании её элементов. Г. преобразований, оставляющих свойства системы инвариантными, наз. группой симметрии. Напр., Г. симметрии равностороннего треугольника содержит повороты вокруг его центра на углы, кратные 120 , и отражения относительно осей, каждая из к-рых проходит через центр и одну из вершин. Практически важный пример - непрерывные симметрии, с к-рыми в физике связаны сохранения законы (см. Нетер теорема, Симметрия законов физики).
Первые применения теории Г. в физике были связаны с выделением геом. элементов симметрии. Так, в 1890 E. С. Фёдоров нашёл все возможные Г. симметрии кристаллов (кристаллографические, или фёдоровские Г.). Квантовомеханич. теория атома водорода, построенная в 20-х гг., существенно опиралась на тот факт, что атом водорода обладает центр. симметрией, т. е. его свойства инвариантны относительно группы вращений (см. Вращений группа). Понимание таких характеристик элементарных частиц, как масса и спин, было достигнуто в рамках теоретико-группового подхода [Ю. П. Вигнер (E. P. Wigner), 1939], когда стало понятно, что симметрии релятивистской элементарной частицы описываются Г. движений пространства-времени, в к-ром она распространяется ( Пуанкаре группой).
В нач. 50-х гг. было введено понятие внутренней симметрии, связанной не со структурой пространства-времени, а с нек-рыми свойствами взаимодействий ( изотопическая инвариантность, унитарная симметрия). В 60-х гг. развивается теория калибровочных полей, или Янга - Миллса полей, где гл. роль играет Г. калибровочных преобразований, к-рая получается, если преобразования из Г. внутр. симметрии совершать в разных точках независимо друг от друга. Развитие теории калибровочных полей повысило интерес физиков к совр. теории Г. Групповые методы существенны также в теории перенормировок (см. Ренормализационная группа).
Теоретико-групповые методы применяют в спектроскопии атомов и молекул (см. Симметрия молекул, Перестановок группа), ядерной физике, квантовой теории поля, квантовой механике, физике твёрдого тела, теории ур-ний матем. физики. В приложениях используют гл. обр. теорию представлений групп, т. е. реализаций Г. преобразованиями линейного пространства. Эта теория позволяет извлекать количеств. следствия из одного лишь факта, что физ. система обладает той или иной симметрией.
Основные определения. Операция умножения в группе G каждой (упорядоченной) паре элементов g, g' ставит в соответствие третий элемент
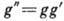 , наз. их произведением. Эта операция должна удовлетворять групповым аксиомам: 1) она ассоциативна,
, наз. их произведением. Эта операция должна удовлетворять групповым аксиомам: 1) она ассоциативна, 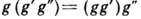 ; 2) существует элемент е, наз. групповой единицей, умножение на к-рую ничего не меняет,
; 2) существует элемент е, наз. групповой единицей, умножение на к-рую ничего не меняет, 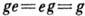 ; 3) для любого элемента g существует обратный элемент
; 3) для любого элемента g существует обратный элемент 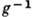 , к-рый при умножении на g даёт единицу,
, к-рый при умножении на g даёт единицу, 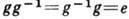 . Умножение в Г., вообще говоря, не перестановочно,
. Умножение в Г., вообще говоря, не перестановочно, 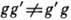 . Г., для к-рых умножение перестановочно (коммутативно), наз. коммутативными или абелевыми. В таких Г. групповая операция часто наз. не умножением, а сложением, вместо gg' используют обозначение g+g', а элемент е наз. нулем.
. Г., для к-рых умножение перестановочно (коммутативно), наз. коммутативными или абелевыми. В таких Г. групповая операция часто наз. не умножением, а сложением, вместо gg' используют обозначение g+g', а элемент е наз. нулем.
С точки зрения групповой структуры, природа элементов Г. несущественна. Г. задана, если любым способом описаны все её элементы и определена групповая операция над ними. Напр., в конечной Г. (содержащей конечное число элементов, наз. порядком Г.) групповую операцию можно задать с помощью табл. умножения. В приложениях Г. возникает обычно в некрои конкретной реализации, её элементами могут быть, напр., числа, матрицы, операторы и т. д. При этом групповую операцию можно задавать как сложение или умножение чисел, умножение матриц или операторов и т. п. Наиб. распространение имеет реализация элементов Г. как преобразований, т. е. взаимно однозначных отображений разл. множеств на себя, g : X->X. Групповой операцией в этом случае является к о м п о з и ц и я отображений,
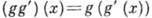 , такое определение гарантирует ассоциативность умножения.
, такое определение гарантирует ассоциативность умножения.
Часто группу G задают как Г. всех преобразований данного множества X, сохраняющих нек-рую матем. структуру, введённую на этом множестве. Так, если X - конечное множество (без какой бы то ни было дополнит. структуры), то G состоит из всех перестановок точек X; если X - векторное пространство, то G - совокупность всех линейных невырожденных преобразований Х; если X - вещественное евклидово (соответственно комплексное гильбертово) пространство, то G - совокупность ортогональных (соответственно унитарных) преобразований; если X - гладкое многообразие (точки к-рою в каждой достаточно малой окрестности задаются координатами, а переход от одной системы координат к другой описывается гладкими ф-циями), то G- совокупность всех диффеоморфизмов (взаимно однозначных преобразований, описывающихся гладкими ф-циями в любой системе координат).
Подмножество К в группе G наз. подгруппой, если оно само является Г. относительно той же групповой операции. Подмножество gK, состоящее из элементов вида gk, где
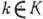 , наз. левым смежным классом элемента g по подгруппе К. Два смежных класса g, g'К либо не имеют ни одного общего элемента, либо полностью совпадают (последнее имеет место при
, наз. левым смежным классом элемента g по подгруппе К. Два смежных класса g, g'К либо не имеют ни одного общего элемента, либо полностью совпадают (последнее имеет место при 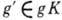 ). T. о., группа G разбивается на непересекающиеся смежные классы. Можно рассматривать смежные классы как элементы нек-рого нового множества. Оно наз. фактор-пространством Г. G по подгруппе К и обозначается G/K. Аналогично можно ввести и правые смежные классы Kg, к-рые также осуществляют (вообще говоря, другое) разбиение Г. Множество правых классов также наз. фактор-пространством и обозначается КС.
). T. о., группа G разбивается на непересекающиеся смежные классы. Можно рассматривать смежные классы как элементы нек-рого нового множества. Оно наз. фактор-пространством Г. G по подгруппе К и обозначается G/K. Аналогично можно ввести и правые смежные классы Kg, к-рые также осуществляют (вообще говоря, другое) разбиение Г. Множество правых классов также наз. фактор-пространством и обозначается КС.
Подгруппа
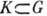 наз. инвариантной подгруппой (или нормальным делителем), если для любого
наз. инвариантной подгруппой (или нормальным делителем), если для любого 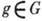 имеет место
имеет место 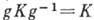 (т. е.
(т. е. 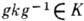 , коль скоро
, коль скоро 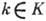 ). В случае инвариантной подгруппы правые смежные классы совпадают с левыми, Kg= gK.B этом случае умножение на Г. естеств. образом определяет умножение смежных классов:
). В случае инвариантной подгруппы правые смежные классы совпадают с левыми, Kg= gK.B этом случае умножение на Г. естеств. образом определяет умножение смежных классов: 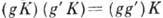 , так что фактор-пространство G/К превращается в Г. Эта Г. наз. фактор-группой G по К. Напр., в группе Пуанкаре P выделяют две подгруппы: Г. трансляций T и Лоренца группу L. Подгруппа T инвариантна в P. Фактор-группа P/T изоморфна L (об изоморфизме см. ниже). Примером инвариантной подгруппы является центр группы G, т. е. множество элементов, каждый из к-рых коммутирует со всеми остальными элементами Г.
, так что фактор-пространство G/К превращается в Г. Эта Г. наз. фактор-группой G по К. Напр., в группе Пуанкаре P выделяют две подгруппы: Г. трансляций T и Лоренца группу L. Подгруппа T инвариантна в P. Фактор-группа P/T изоморфна L (об изоморфизме см. ниже). Примером инвариантной подгруппы является центр группы G, т. е. множество элементов, каждый из к-рых коммутирует со всеми остальными элементами Г.
Отображение
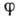 :
:  , одной Г. на другую наз. изоморфизмом, если это отображение взаимно однозначно и согласовано с групповым умножением в обеих Г., т. е. если
, одной Г. на другую наз. изоморфизмом, если это отображение взаимно однозначно и согласовано с групповым умножением в обеих Г., т. е. если 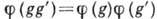 для любых g,
для любых g, 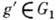 . В этом случае Г. G1 и G2 наз. изоморфными, что обозначают
. В этом случае Г. G1 и G2 наз. изоморфными, что обозначают 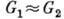 или G1=G2. Изоморфизм
или G1=G2. Изоморфизм
Г. на ту же самую Г. (на себя) наз. автоморфизмом. Изоморфные Г. не отличаются с точки зрения своей внутр. групповой структуры. Когда говорят об абстрактной Г., имеют в виду, что Г. задана с точностью до изоморфизма (т. е. задан на самом деле лишь класс изоморфных друг другу Г.). Наоборот, конкретная реализация Г. означает выбор одной определенной Г. из класса изоморфных. Напр., Г.
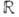 всех веществ. чисел со сложением в качестве групповой операции изоморфна Г.
всех веществ. чисел со сложением в качестве групповой операции изоморфна Г. 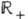 положит. чисел с умножением в качестве групповой операции (изоморфизм в одном направлении осуществляется операцией ехр, в обратном - операцией ln). Можно считать, что
положит. чисел с умножением в качестве групповой операции (изоморфизм в одном направлении осуществляется операцией ехр, в обратном - операцией ln). Можно считать, что 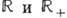 это разные реализации одной и той же абстрактной Г. Ещё одной реализацией той же Г. является Г. сдвигов (трансляций) веществ. прямой. Точно так же разл. реализациями одной и той же абстрактной Г. являются окружность (со сложением углов в качестве групповой операции), Г. движений окружности, Г. поворотов плоскости и Г. всех комплексных чисел, по модулю равных единице (с умножением в качестве групповой операции). Соответствующую абстрактную Г. часто обозначают через
это разные реализации одной и той же абстрактной Г. Ещё одной реализацией той же Г. является Г. сдвигов (трансляций) веществ. прямой. Точно так же разл. реализациями одной и той же абстрактной Г. являются окружность (со сложением углов в качестве групповой операции), Г. движений окружности, Г. поворотов плоскости и Г. всех комплексных чисел, по модулю равных единице (с умножением в качестве групповой операции). Соответствующую абстрактную Г. часто обозначают через 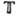 или
или 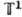 (одномерный тор, т. е. окружность).
(одномерный тор, т. е. окружность).
Более общим, чем изоморфизм, является понятие гомоморфизма Г. Отображение
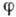 :
:  одной Г. в другую наз. гомоморфизмом, если оно согласовано с групповым умножением в обеих Г. В этом случае не требуется, чтобы образ отображения
одной Г. в другую наз. гомоморфизмом, если оно согласовано с групповым умножением в обеих Г. В этом случае не требуется, чтобы образ отображения 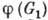 совпадал с группой G2. Он может быть подгруппой в G2. Не требуется и взаимной однозначности отображения, так что одному элементу в
совпадал с группой G2. Он может быть подгруппой в G2. Не требуется и взаимной однозначности отображения, так что одному элементу в 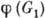 может соответствовать более чем один прообраз в G1. Множество прообразов единицы,
может соответствовать более чем один прообраз в G1. Множество прообразов единицы, 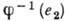 , образует в G1 инвариантную подгруппу, наз. ядром гомоморфизма. Факторгруппа
, образует в G1 инвариантную подгруппу, наз. ядром гомоморфизма. Факторгруппа 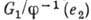 изоморфна группе
изоморфна группе 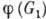 .
.
Если G' - группа линейных преобразований (невырожденных операторов) в нек-ром линейном пространстве L, то гомоморфизм U:
 . наз. представлением группы G (точнее, линейным представлением). T. о., линейное представление каждому элементу g группы G ставит в соответствие невырожденный линейный оператор U(g), причём произведению элементов
. наз. представлением группы G (точнее, линейным представлением). T. о., линейное представление каждому элементу g группы G ставит в соответствие невырожденный линейный оператор U(g), причём произведению элементов 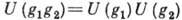 Г. соответствует произведение операторов,
Г. соответствует произведение операторов,
В более общем случае, когда G' - Г. преобразований множества X любой природы, говорят, что гомоморфизм
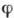 :
:  определяет действие группы G на X (иногда такой гомоморфизм наз. нелинейным представлением группы). Вместо
определяет действие группы G на X (иногда такой гомоморфизм наз. нелинейным представлением группы). Вместо 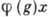 результат действия элемента g на точку x обозначают иногда gx.
результат действия элемента g на точку x обозначают иногда gx.
Пространство X, на к-ром задано действие группы G, наз. G- пространством. Если Г. действует транзитивно, т. е. для любой пары точек х,
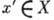 найдётся элемент группы g, переводящий одну из этих точек в другую, x'=gx, то X наз. однородным пространством. Фактор-пространство всегда является однородным пространством. Напр., группа Лоренца L не является инвариантной подгруппой в группе Пуанкаре P, поэтому фактор-пространство P/L является однородным пространством, но не факторгруппой. Любое G -пространство представляется в виде объединения непересекающихся подпространств, в каждом из к-рых Г. действует транзитивно. Эти подпространства наз. областями транзитивности или орбитами группы. Стационарной подгруппой (стабилизатором) нек-рой точки
найдётся элемент группы g, переводящий одну из этих точек в другую, x'=gx, то X наз. однородным пространством. Фактор-пространство всегда является однородным пространством. Напр., группа Лоренца L не является инвариантной подгруппой в группе Пуанкаре P, поэтому фактор-пространство P/L является однородным пространством, но не факторгруппой. Любое G -пространство представляется в виде объединения непересекающихся подпространств, в каждом из к-рых Г. действует транзитивно. Эти подпространства наз. областями транзитивности или орбитами группы. Стационарной подгруппой (стабилизатором) нек-рой точки 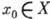 наз. множество элементов Г., оставляющих эту точку на месте.
наз. множество элементов Г., оставляющих эту точку на месте.
Прямым произведением групп G1 и G2 наз. множество пар (g1,g2), где
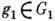 ,
, 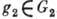 , с определённой на этом множестве операцией умножения
, с определённой на этом множестве операцией умножения 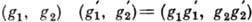 . T. о., прямое произведение Г. также является Г., к-рая обозначается
. T. о., прямое произведение Г. также является Г., к-рая обозначается  или
или 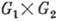 . Если Г.-сомножители совпадают, то используется обозначение
. Если Г.-сомножители совпадают, то используется обозначение 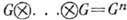 . Если Г.-сомножители коммутативны, то их прямое произведение - также коммутативная Г. В этом случае иногда вместо термина "прямое произведение" употребляют термин "прямая сумма" и вводят обозначение
. Если Г.-сомножители коммутативны, то их прямое произведение - также коммутативная Г. В этом случае иногда вместо термина "прямое произведение" употребляют термин "прямая сумма" и вводят обозначение  или
или 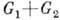 .
.
Топологические типы групп. Обычно встречающиеся на практике Г. являются топологич. группами. Это значит, что для элементов Г. определено понятие предельного перехода, причём операция умножения и переход к обратному элементу непрерывны (т. е., если
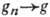 и
и 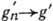 при
при  , то
, то 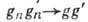 и
и 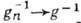 ). С точки зрения топологии выделяются след. типы Г.
). С точки зрения топологии выделяются след. типы Г.
1. Дискретные группы. Это Г. с тривиальной топологией: последовательность
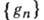 сходится только тогда, когда она стабилизируется, т. е. все её элементы, начиная с нек-рого, равны,
сходится только тогда, когда она стабилизируется, т. е. все её элементы, начиная с нек-рого, равны, 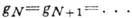 Дискретными являются, напр., все конечные Г. и кристаллографич. Г. (Г. симметрии кристаллич. решёток).
Дискретными являются, напр., все конечные Г. и кристаллографич. Г. (Г. симметрии кристаллич. решёток).
2. Компактные группы. Это Г., в к-рых из каждой последовательности
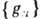 можно выделить сходящуюся подпоследовательность. Компактные Г. имеют "конечный объём". Более точно, инвариантная мера Г. конечна в том и только в том случае, если Г. компактна (мера на Г. наз. инвариантной, если меры подмножеств В и gB равны для любого подмножества
можно выделить сходящуюся подпоследовательность. Компактные Г. имеют "конечный объём". Более точно, инвариантная мера Г. конечна в том и только в том случае, если Г. компактна (мера на Г. наз. инвариантной, если меры подмножеств В и gB равны для любого подмножества 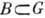 и элемента
и элемента 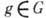 ). Среди дискретных Г. компактными являются только конечные Г. Примеры компактных Г.: Г. вращений окружности и сферы (и вообще Г. движений компактны многообразий), Г. унитарных преобразований в конечномерном гильбертовом пространстве U(п )и Г. ортогональных преобразований в конечномерном евклидовом пространстве О(п).
). Среди дискретных Г. компактными являются только конечные Г. Примеры компактных Г.: Г. вращений окружности и сферы (и вообще Г. движений компактны многообразий), Г. унитарных преобразований в конечномерном гильбертовом пространстве U(п )и Г. ортогональных преобразований в конечномерном евклидовом пространстве О(п).
3. Локально компактные группы. Это такие Г., в к-рых каждый элемент обладает компактной окрестностью. Этот класс Г. очень широк: он содержит все дискретные и все компактные Г., а также все конечномерные группы Ли (см. ниже). Характеристическим свойством локально компактной Г. является наличие инвариантной меры на ней (т. н. меры Хаара). К классу локально компактных относится большая часть Г., используемых в физике.
4. Группы Ли (ГЛ) отличаются тем, что их элементы можно охарактеризовать конечным набором числовых параметров, т. е. на Г. можно ввести систему координат (см. ниже).
5. Бесконечномерные группы Ли являются обобщением ГЛ. Элементы таких Г. характеризуются заданием бесконечного набора числовых параметров (или нек-рого количества ф-ций). В физике используют в осн. Г. линейных операторов в бесконечномерных линейных пространствах, Г. диффеоморфизмов гладких многообразий и Г. калибровочных преобразований. Теория таких Г. разработана в гораздо меньшей степени, чем теория обычных (конечномерных) ГЛ. Большинство результатов здесь носит отрицат. характер: эти Г. не являются локально компактными, на них не существует инвариантного интеграла, они могут не иметь полной системы унитарных представлений.
Алгебраические типы групп. С точки зрения алгебраич. (групповой) структуры среди всех Г. выделяют след. типы.
1.Коммутативные (абелевы) группы. Это Г., для к-рых любые два элемента перестановочны: gg'=g'g. Простейшими дискретными коммутативными Г. являются Г. целых чисел
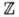 (групповая операция - сложение) и Г.
(групповая операция - сложение) и Г. 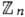 вычетов по модулю п (она получается из
вычетов по модулю п (она получается из 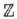 , если элементом Г. считать класс целых чисел, отличающихся друг от друга на числа, кратные п). Простейшими непрерывными коммутативными Г. являются Г.
, если элементом Г. считать класс целых чисел, отличающихся друг от друга на числа, кратные п). Простейшими непрерывными коммутативными Г. являются Г. 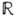 всех веществ. чисел (групповая операция - сложение) и Г.
всех веществ. чисел (групповая операция - сложение) и Г.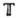 -SO(2) поворотов плоскости.
-SO(2) поворотов плоскости.
Всякая связная коммутативная одномерная Г. изоморфна либо
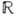 ,либо
,либо 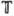 (связной наз. Г., любые два , элемента к-рой можно соединить непрерывной кривой, целиком принадлежащей Г.). Всякая связная коммутативная ГЛ изоморфна прямому произведению таких Г., т. е.
(связной наз. Г., любые два , элемента к-рой можно соединить непрерывной кривой, целиком принадлежащей Г.). Всякая связная коммутативная ГЛ изоморфна прямому произведению таких Г., т. е.  (
(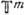 - m-мерный тор). Дискретную Г. ,. удобно описывать с помощью её образующих, т. е. таких элементов, что всякий элемент Г. представляется в виде произведения элементов-образующих. Г. с одной образующей (циклическая) изоморфна либо
- m-мерный тор). Дискретную Г. ,. удобно описывать с помощью её образующих, т. е. таких элементов, что всякий элемент Г. представляется в виде произведения элементов-образующих. Г. с одной образующей (циклическая) изоморфна либо 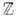 , либо
, либо 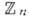 . Любая дискретная коммутативная Г. с конечным числом образующих является прямым произведением циклич. групп, т. е. изоморфна (набор чисел п 1, ..., nS не определяется
. Любая дискретная коммутативная Г. с конечным числом образующих является прямым произведением циклич. групп, т. е. изоморфна (набор чисел п 1, ..., nS не определяется 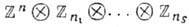 однозначно заданием Г.). Важными для физики примерами коммутативных Г. являются Г. трансляций n -мерного евклидова или псевдоевклидова пространства, изоморфная
однозначно заданием Г.). Важными для физики примерами коммутативных Г. являются Г. трансляций n -мерного евклидова или псевдоевклидова пространства, изоморфная 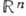 , и Г. трансляций n -мерной решетки, изоморфная
, и Г. трансляций n -мерной решетки, изоморфная 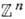
2. Разрешимые группы. Группа G наз. разрешимой, если в ней есть конечная цепочка вложенных друг в друга подгрупп
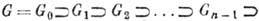
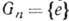 , обладающая свойствами: a) Gk+1- инвариантная подгруппа в Gk б) фактор-группа
, обладающая свойствами: a) Gk+1- инвариантная подгруппа в Gk б) фактор-группа 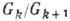 коммутативна. Изучение разрешимых Г. в большой степени сводится к изучению коммутативных Г. Абелева ГЛ разрешима. Пример разрешимой Г.- группа движений евклидовой плоскости. Термин "разрешимая" отражает роль этих Г. в теории алгебраич. и дифференц. ур-ний. А именно: алгебраич. ур-ние n- йстепени разрешимо в радикалах (соответственно обыкновенное дифференц. ур-ние n-го порядка разрешимо в квадратурах), если и только если его т. п. группа Галуа (соответственно группа Ли - Ритта- Колчина) разрешима.
коммутативна. Изучение разрешимых Г. в большой степени сводится к изучению коммутативных Г. Абелева ГЛ разрешима. Пример разрешимой Г.- группа движений евклидовой плоскости. Термин "разрешимая" отражает роль этих Г. в теории алгебраич. и дифференц. ур-ний. А именно: алгебраич. ур-ние n- йстепени разрешимо в радикалах (соответственно обыкновенное дифференц. ур-ние n-го порядка разрешимо в квадратурах), если и только если его т. п. группа Галуа (соответственно группа Ли - Ритта- Колчина) разрешима.
3. Нильпотентные группы. Группа G наз. нильпотентной, если она разрешима и, кроме того, для любого
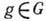 и любого
и любого 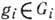 элемент
элемент 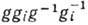 (наз. коммутатором g и gi )лежит в Gi+1. Др. словами, все Gi инвариантны в G и группа Gi/Gi+1 принадлежит центру группы G/Gi+1.
(наз. коммутатором g и gi )лежит в Gi+1. Др. словами, все Gi инвариантны в G и группа Gi/Gi+1 принадлежит центру группы G/Gi+1.
4. Простые группы. Это класс Г., наиб. далёкий от класса коммутативных Г. Группа G наз. простой, если она не содержит инвариантных подгрупп, отличных от самой Г. иединичной подгруппы. Примером простых Г. являются Г. PSU(п )проективной унитарной симметрии. Прямое произведение простых Г. иногда наз. полупростой группой (полупростая Г. характеризуется отсутствием абелевых инвариантных подгрупп). Описание всех простых ГЛ известно (см. Ли алгебра), а описание всех конечных простых Г. близится к завершению.
5. Расширения групп. Пусть в группе G есть инвариантная подгруппа G0. Обозначим факторгруппу G/G0 через G1. Говорят, что G является расширением G1 с помощью G0. Предположим, что в каждом смежном классе gG0 можно выбрать по одному представителю так, чтобы произведение представителей было представителем. Тогда множество представителей образует подгруппу группы G, изоморфную G1. В этом случае говорят, что расширение тривиально или что G является полупрямым произведением G1 на G0. Напр., группа Пуанкаре является полупрямым произведением группы Лоренца на Г. 4-мерных трансляций, а Г. движений евклидова пространства - полупрямым произведением Г. вращений на Г. трансляций. В теории Г. разработаны методы (когомологии групп), позволяющие описывать все расширения с заданными G1 и G0. Для широкого класса Г. (напр., для конечных Г. и для связных ГЛ) доказано, что каждая из них является расширением полупростой Г. с помощью разрешимой Г. Большинство кристаллографич. Г. являются нетривиальными расширениями нек-рой конечной Г. вращений и отражений с помощью дискретной Г. трансляций. Тривиальными расширениями (полупрямыми произведениями) являются Г. движений евклидовых и псевдоевклидовых пространств, в т. ч. группа Пуанкаре.
Группы Ли. Элементы ГЛ задают конечным набором числовых параметров (координат) так, что групповое умножение и переход к обратному элементу выражаются с помощью гладких (бесконечно дифференцируемых) ф-ций от этих параметров. Число параметров наз. размерностью ГЛ. Параметры могут быть вещественными или комплексными, в соответствии с этим ГЛ наз. вещественной или комплексной ГЛ. Каждую комплексную ГЛ можно рассматривать как веществ. ГЛ вдвое большей размерности. Примерами ГЛ являются физически важные Г. трансляций, вращений, конформных и унитарных преобразований разных размерностей, группа Лоренца, группа Пуанкаре и т. д. ГЛ в целом может обладать такой топологией, что её невозможно покрыть одной системой координат. Это имеет место даже для такой простой ГЛ, как Г. поворотов плоскости, SO(2). Топологически эта Г. эквивалентна окружности и не может быть гладко отображена на веществ. прямую (ось координат) или к.-л. интервал этой прямой.
Поэтому в общем случае на ГЛ вводят целое семейство систем координат (карт), каждая из них покрывает нек-рую область Г. (координатную окрестность). На пересечении любых двух координатных окрестностей, где имеют смысл сразу две системы координат, переход от одной из них к другой описывается с помощью гладких (бесконечно дифференцируемых) ф-ций. Операция умножения в Г. и переход к обратному элементу в любой системе координат описываются гладкими (бесконечно дифференцируемыми) ф-циями. Сказанное можно сформулировать след. образом: ГЛ - это группа, к-рая одновременно является гладким многообразием, причём групповая структура согласована со структурой многообразия.
Для определения алгебры Ли пользуются матричной реализацией (линейным представлением) Г.: пусть каждый элемент g группы G представляет собой матрицу (или, что то же, линейный оператор в конечномерном линейном пространстве). Элемент g характеризуется набором числовых параметров (координат на Г.), g=S(x1, ..., х п).
Условимся выбирать эти параметры так, чтобы единице Г. соответствовали нулевые значения параметров, e=g(0,...,0). Тогда инфинитезимальным оператором (генератором) Г. G наз. производная от ф-ции g по одному из параметров, взятая в единице Г.:
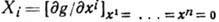 Ясно, что генераторы являются матрицами (операторами) той же размерности, что и элементы Г. Оказывается, что коммутатор двух генераторов линейно выражается через генераторы:
Ясно, что генераторы являются матрицами (операторами) той же размерности, что и элементы Г. Оказывается, что коммутатор двух генераторов линейно выражается через генераторы: 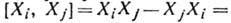
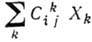 . Числа
. Числа 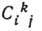 наз. структурными константами Г. Существенно, что набор структурных констант не зависит от того, какая матричная реализация (представление) Г. выбрана для определения операторов Xi. Поэтому структурные константы характеризуют не конкретное представление, а саму Г. В то же время структурные константы зависят от выбора системы координат вблизи единицы Г. При изменении системы координат структурные константы меняются как тензоры. Выбором системы координат обычно добиваются, чтобы набор структурных констант был по возможности более простым. Для полупростой ГЛ можно построить из генераторов скалярный квадратичный оператор С, наз. оператором Казимира:
наз. структурными константами Г. Существенно, что набор структурных констант не зависит от того, какая матричная реализация (представление) Г. выбрана для определения операторов Xi. Поэтому структурные константы характеризуют не конкретное представление, а саму Г. В то же время структурные константы зависят от выбора системы координат вблизи единицы Г. При изменении системы координат структурные константы меняются как тензоры. Выбором системы координат обычно добиваются, чтобы набор структурных констант был по возможности более простым. Для полупростой ГЛ можно построить из генераторов скалярный квадратичный оператор С, наз. оператором Казимира: 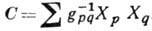 , где
, где 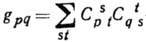 -метрич. тензор Картана.
-метрич. тензор Картана.
Операторы Xi, i=1, ..., n, образуют базис алгебры Ли. Произвольный элемент алгебры является линейной комбинацией базисных элементов,
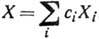 .
.
Т. о., алгебра Ли группы Ли G является касательным пространством к многообразию G в точке е.
Можно определить структурные константы и не обращаясь к матричной реализации (линейному представлению) Г. Пусть в нек-рой системе координат закон умножения в ГЛ имеет вид
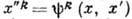 , так что g (x) g (x')=g(х " )(здесь одной буквой х обозначен весь набор координат х 1, ..., х n). По определению ГЛ, ф-ции yk (х, х' )должны быть бесконечно дифференцируемы. Разложение их в ряд Тейлора имеет вид
, так что g (x) g (x')=g(х " )(здесь одной буквой х обозначен весь набор координат х 1, ..., х n). По определению ГЛ, ф-ции yk (х, х' )должны быть бесконечно дифференцируемы. Разложение их в ряд Тейлора имеет вид
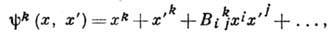
где многоточие обозначает члены более высоких порядков. Тогда величины
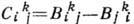 являются структурными константами и определяют соответствующую алгебру Ли. Существуют также способы построения алгебры Ли по ГЛ, не использующие явно систему координат. Для изучения ГЛ важны однопараметрич. подгруппы (т. е. одномерные ГЛ). Параметр t в такой подгруппе выбирают так, чтобы выполнялись равенства х(0)=е, x(t) x(s)-x(t+s). Существует взаимно однозначное соответствие между однопараметрич. подгруппами в ГЛ G и элементами её алгебры Ли
являются структурными константами и определяют соответствующую алгебру Ли. Существуют также способы построения алгебры Ли по ГЛ, не использующие явно систему координат. Для изучения ГЛ важны однопараметрич. подгруппы (т. е. одномерные ГЛ). Параметр t в такой подгруппе выбирают так, чтобы выполнялись равенства х(0)=е, x(t) x(s)-x(t+s). Существует взаимно однозначное соответствие между однопараметрич. подгруппами в ГЛ G и элементами её алгебры Ли 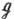 : подгруппе х(t )соответствует касательный вектор
: подгруппе х(t )соответствует касательный вектор 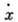 (0). Экспоненциальное отображение алгебры Ли
(0). Экспоненциальное отображение алгебры Ли 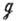 в ГЛ G определяют так:
в ГЛ G определяют так: 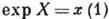 , где х(t) - однопараметрич. подгруппа, соответствующая элементу X. Для матричных ГЛ отображение ехр совпадает с обычной экспонентой:
, где х(t) - однопараметрич. подгруппа, соответствующая элементу X. Для матричных ГЛ отображение ехр совпадает с обычной экспонентой: 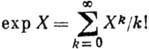 . Обратное отображение (определённое только в нек-рой окрестности единицы) иногда обозначают ln. С помощью экспоненц. отображения в ГЛ G определяют канонич. систему координат: координатами точки g= ехр X служат коэф. разложения X = lng по базису в алгебре Ли:
. Обратное отображение (определённое только в нек-рой окрестности единицы) иногда обозначают ln. С помощью экспоненц. отображения в ГЛ G определяют канонич. систему координат: координатами точки g= ехр X служат коэф. разложения X = lng по базису в алгебре Ли: 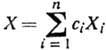 . Осн. свойство экспоненц. отображения - его функториальность, к-рая выражается коммутативной диаграммой:
. Осн. свойство экспоненц. отображения - его функториальность, к-рая выражается коммутативной диаграммой:
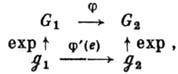
где
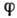 -любой гомоморфизм ГЛ G1 в ГЛ G2, а
-любой гомоморфизм ГЛ G1 в ГЛ G2, а 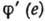 - производная отображения в точке е. Это значит, что в канонич. координатах любой гомоморфизм ГЛ записывается линейными ф-циями.
- производная отображения в точке е. Это значит, что в канонич. координатах любой гомоморфизм ГЛ записывается линейными ф-циями.
Наиб. важными примерами ГЛ являются Г. GL(n, R) всех невырожденных (обратимых)
 матриц с веществ. элементами и Г. GL(п, С) всех невырожденных
матриц с веществ. элементами и Г. GL(п, С) всех невырожденных 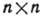 матриц с комплексными элементами. Координатами в этих Г. могут служить сами матричные элементы. Поэтому
матриц с комплексными элементами. Координатами в этих Г. могут служить сами матричные элементы. Поэтому 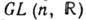 -это веществ. ГЛ размерности п 2, а
-это веществ. ГЛ размерности п 2, а 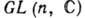 -комплексная ГЛ размерности n2 (к-рую можно рассматривать как веществ. ГЛ размерности 2n2). Алгеброй Ли группы GL(п, R)[соответственно
-комплексная ГЛ размерности n2 (к-рую можно рассматривать как веществ. ГЛ размерности 2n2). Алгеброй Ли группы GL(п, R)[соответственно 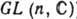 ] является пространство всех
] является пространство всех 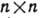 матриц с веществ. (соответственно комплексными) элементами. Она обозначается через
матриц с веществ. (соответственно комплексными) элементами. Она обозначается через 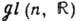 [соответственно
[соответственно 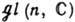 ].
].
В назв. матричных ГЛ отражены свойства их элементов. В общем случае ставят букву L (линейность), унитарность отмечают буквой U, ортогональность -буквой О. Если матрицы имеют единичный определитель (унимодулярны), в назв. Г. ставят букву S. В скобках после названия указывают ранг (число строк) матриц, образующих Г. Если ГЛ G реализована как подгруппа в GL (п,R) или GL (п, С), то её алгебра Ли
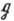 является подалгеброй в
является подалгеброй в 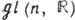 или
или 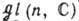 . Напр., Г. О(п )ортогональных матриц и Г. SO(n) ортогональных унимодулярных матриц имеют одну и ту же алгебру Ли so( п), состоящую из всех антисимметричных веществ. матриц; группе
. Напр., Г. О(п )ортогональных матриц и Г. SO(n) ортогональных унимодулярных матриц имеют одну и ту же алгебру Ли so( п), состоящую из всех антисимметричных веществ. матриц; группе 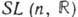 веществ. унимодулярных матриц соответствует алгебра Ли
веществ. унимодулярных матриц соответствует алгебра Ли 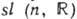 , состоящая из матриц с нулевым следом; группе U (п )унитарных матриц соответствует алгебра Ли и (п )антиэрмитовых матриц (т. е. таких, что
, состоящая из матриц с нулевым следом; группе U (п )унитарных матриц соответствует алгебра Ли и (п )антиэрмитовых матриц (т. е. таких, что 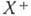 = - X).
= - X).
Тесная связь между ГЛ и алгеброй Ли позволяет свести изучение представлений ГЛ к изучению представлений алгебры Ли. В конечном счёте задача сводится к исследованию представлений генераторов Г. Задать такое представление - значит задать п матриц (или в общем случае линейных операторов) Xi, удовлетворяющих коммутац. соотношениям с заданным набором структурных констант. Именно эту методику (инфинитезимальный подход) обычно используют при изучении представлений ГЛ.
Алгебра Ли характеризует лишь локальные свойства ГЛ, т. е. такие, к-рые можно сформулировать в терминах достаточно малой окрестности единицы. В частности, для определения алгебры Ли достаточно ввести координаты лишь в нек-рой окрестности единицы.
Отображение
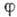 :
: 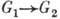 одной ГЛ на другую ГЛ наз. изоморфизмом групп Ли, если оно взаимно однозначно, согласовано с групповым умножением в каждой Г. и является гладким (т. е. в любой системе координат выражается гладкими ф-циями). ГЛ G1 и G2 в этом случае наз. изоморфными. Две ГЛ наз. локально изоморфными, если изоморфизм определён в нек-рой окрестности единицы (но, вообще говоря, не продолжается на всю Г.). Локально изоморфные ГЛ имеют одинаковые (изоморфные) алгебры Ли. Обратно, если две ГЛ имеют изоморфные алгебры Ли, то они локально изоморфны.
одной ГЛ на другую ГЛ наз. изоморфизмом групп Ли, если оно взаимно однозначно, согласовано с групповым умножением в каждой Г. и является гладким (т. е. в любой системе координат выражается гладкими ф-циями). ГЛ G1 и G2 в этом случае наз. изоморфными. Две ГЛ наз. локально изоморфными, если изоморфизм определён в нек-рой окрестности единицы (но, вообще говоря, не продолжается на всю Г.). Локально изоморфные ГЛ имеют одинаковые (изоморфные) алгебры Ли. Обратно, если две ГЛ имеют изоморфные алгебры Ли, то они локально изоморфны.
ГЛ наз. односвязной, если любая замкнутая кривая в этой Г. может быть непрерывной деформацией стянута в точку. Для любой ГЛ G совокупность G0 тех её элементов, к-рые можно соединить с единицей непрерывной кривой, образует максимальную связную подгруппу в G, наз. связной компонентой единицы Г. G. Подгруппа G0 инвариантна в G, а фактор-группа G/G0 дискретна. Напр., для Г. О(п )связной компонентой единицы является подгруппа SO(п). Фактор-группа O(n)/SO(n )состоит из двух элементов. Связная ГЛ G является разрешимой (соответственно нильпотентной, почти простой, полупростой), если и только если её алгебра Ли
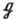 разрешима (соответственно нильпотентна, проста, полупроста).
разрешима (соответственно нильпотентна, проста, полупроста).
Среди всех связных ГЛ, локально изоморфных данной Г. G, есть ровно одна односвязная Г.
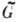 , наз. универсальной накрывающей Г. G. Все прочие Г., локально изоморфные G, являются фактор-группами
, наз. универсальной накрывающей Г. G. Все прочие Г., локально изоморфные G, являются фактор-группами 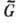 по различным дискретным инвариантным подгруппам, принадлежащим центру Г.
по различным дискретным инвариантным подгруппам, принадлежащим центру Г. 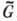 . Напр., все коммутативные связные ГЛ размерности п локально изоморфны. Односвязной Г. среди них (универсальной накрывающей для всех них) является
. Напр., все коммутативные связные ГЛ размерности п локально изоморфны. Односвязной Г. среди них (универсальной накрывающей для всех них) является 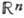 -евклидово n -мерное пространство со сложением в качестве групповой операции (или Г. трансляций этого пространства). Произвольная Г. из этого класса имеет вид
-евклидово n -мерное пространство со сложением в качестве групповой операции (или Г. трансляций этого пространства). Произвольная Г. из этого класса имеет вид 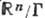 , где Г- нек-рая решётка (дискретная подгруппа) в
, где Г- нек-рая решётка (дискретная подгруппа) в 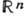 . Если группа Г порождена k линейно независимыми векторами, то
. Если группа Г порождена k линейно независимыми векторами, то 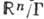 изоморфна
изоморфна 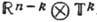 .
.
Всякая ГЛ локально изоморфна нек-рой матричной Г. Для мн. типов ГЛ это утверждение верно не только локально, но и в целом (глобально). В частности, все разрешимые, все компактные и все комплексные ГЛ допускают глобальную матричную реализацию.
Всякая связная односвязная ГЛ является полупрямым произведением связной односвязной полупростой
ГЛ на связную односвязную разрешимую ГЛ. Все полупростые ГЛ полностью описаны (см. Ли алгебра), а классификация разрешимых ГЛ доведена до размерности 6.
Лит.: Любарский Г. Я., Теория групп и ее применение в физике, M., 1958; Вигнер E., Теория групп и ее приложения к квантовомеханической теории атомных спектров, пер. с англ., M., 1961; Холл M., Теория групп, пер. с англ., M., 1962; Хамермеш M., Теория групп и ее применение к физическим проблемам, пер. с англ., M., 1966, Лиховский В. Д., Болохов А. А., Группы симметрии и элементарные частицы, Л., 1983; Эллиот Д ж., Добер П., Симметрия в физике, пер. с англ., т. 1-2, M , 1983; Рихтмайер Р., Принципы современной математической физики, пер. с англ., т. 2, M., 1984; Вейль Г., Теория групп и квантовая механика, пер. с англ., M., 1986.
А. А. Кириллов, M. Б. Менский.
Ориентационное и магнитное упорядочения. В изотропной жидкости, состоящей из анизотропных, но случайно ориентированных молекул, может происходить фазовый переход в анизотропную жидкость, в к-рой молекулы имеют преимуществ. ориентацию (см. Жидкие кристаллы). Параметром порядка при таком ориентационном упорядочении является спонтанная поляризация или константа анизотропии диэлектрич. проницаемости
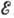 , равные 0 в изотропной жидкости и отличные от 0 в жидком кристалле.
, равные 0 в изотропной жидкости и отличные от 0 в жидком кристалле.
Магн. упорядочение состоит в том, что магн. моменты атомов, ориентированные при высокой темп-ре в разных точках независимо ( парамагнетик), при понижении темп-ры ниже точек Кюри или Нееля упорядочиваются и либо имеют одинаковое направление и ориентацию ( ферромагнетик), либо одинаковое направление, но разные ориентации. В последнем случае они образуют магн. подрешётки, причём ориентации магн. моментов для атомов каждой подрешётки одинаковы, а для атомов разных подрешёток - противоположны ( антиферромагнетик). Параметром порядка в ферромагнетиках является намагниченность.
Упорядочение в квантовых жидкостях. Все перечисленные виды упорядочения имели в качестве параметра порядка классич. величины. Имеется важная группа упорядочивающихся систем, в к-рых параметром порядка является макроскопич. волновая ф-ция всего образца. Такое квантовое упорядочение есть в сверхтекучем состоянии изотопов гелия HeII, 3He- A,3He-B (см. Гелий жидкий, Сверхтекучесть )и в сверхпроводящей фазе металлов (см. Сверхпроводимость). В этих случаях при темп-ре T выше темп-ры фазового перехода
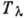 волновые ф-ции всех частиц, относящиеся к удалённым друг от друга точкам пространства, скоррелированы. Упорядоченное состояние характеризуется скоррелированной фазой волновых ф-ций частиц, к-рая может измениться во всём образце в целом, но не может измениться независимо в разных точках.
волновые ф-ции всех частиц, относящиеся к удалённым друг от друга точкам пространства, скоррелированы. Упорядоченное состояние характеризуется скоррелированной фазой волновых ф-ций частиц, к-рая может измениться во всём образце в целом, но не может измениться независимо в разных точках.
Изменение симметрии при упорядочении. В классификации упорядоченных и неупорядоченных фаз важную роль играет симметрия. Напр., в случае сплава в высокотемпературной фазе все узлы решётки эквивалентны, поэтому здесь имеет место инвариантность относительно трансляции на любое число периодов кристаллич. решётки, т. е. непрерывная симметрия. В упорядоченной фазе сплава эквивалентны только узлы, занятые, напр., атомами Cu. Ей отвечает инвариантность относительно таких трансляций, к-рые переводят один из узлов, занятых атомом Cu, в другой (дискретная симметрия). T. о., упорядоченной фазе отвечает более низкая симметрия.
В момент фазового перехода симметрия меняется скачком. Однако параметр порядка, к-рый является количеств. мерой нарушения симметрии, может возникать как скачком, так и непрерывно. Математич. теорией, классифицирующей симметрии разл. фаз, является теория групп. Изучение симметрии упорядоченной и неупорядоченной фаз позволяет, в частности, выяснить тип фазового перехода.
Если при упорядочении нарушается непрерывная симметрия, то говорят, что упорядоченная фаза обладает дополнительной по сравнению с неупорядоченной фазой "жёсткостью". Это означает, что малая деформация требует дополнит. затраты энергии. Напр., при переходе жидкости в кристаллич. состояние нарушается инвариантность относительно трансляции частиц на произвольный вектор а. Следствием этого является появление в твёрдом теле дополнит. жёсткости по отношению к деформации сдвига, к-рая отсутствует в жидкости. В HeII при согласованных изменениях фазы
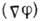 волновой ф-ции возникает дополнит. свободная энергия
волновой ф-ции возникает дополнит. свободная энергия 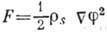 , где
, где 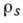 - удельная плотность сверхтекучей компоненты-играет роль коэф. жёсткости. Если переход в упорядоченное состояние является переходом 2-го рода, то в точке перехода
- удельная плотность сверхтекучей компоненты-играет роль коэф. жёсткости. Если переход в упорядоченное состояние является переходом 2-го рода, то в точке перехода
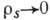 .
.
Примером, когда при упорядочении не возникает дополнит. жёсткости, является упорядочивание сплава. В этом случае в результате упорядочения нарушается не непрерывная, а дискретная симметрия относительно трансляций на периоды исходной решётки.
Упорядочение в одномерных (цепочки) и двумерных (плёнки) системах имеет ряд особенностей: как правило, дальний порядок при любой конечной темп-ре в них отсутствует, но при низких темп-pax есть ближний порядок с большим радиусом корреляции R С . Если при упорядочении нарушается дискретная симметрия, то в двумерном случае возможен дальний порядок. В одномерном же случае дальнего порядка нет, но
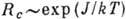 , где J - "выигрыш" в энергии при упорядочении. Если при упорядочении нарушается непрерывная симметрия, то дальнего порядка нет и в двумерных и в одномерных системах;
, где J - "выигрыш" в энергии при упорядочении. Если при упорядочении нарушается непрерывная симметрия, то дальнего порядка нет и в двумерных и в одномерных системах; 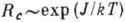 в двумерном или
в двумерном или 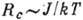 в одномерном случае.
в одномерном случае.
Если между цепочками или плёнками есть слабое взаимодействие, то при высокой темп-ре отсутствуют и дальний и ближний порядок, при понижении темп-ры возникает область ближнего порядка с большим RC , и при самых низких темп-pax возникает дальний порядок (см. Квазиодномерные соединения, Квазидвумерные соединения).
Многократное упорядочение. Вещество, в к-ром уже произошло кристаллич. упорядочение, может при понижении Т испытать вторичное упорядочение, приводящее к дальнейшему понижению симметрии как в координац. расположении атомов (сегнетоэлектрики, сплавы), так и в ориентации магн. моментов (магнетики). Если отношение периодов новой структуры и кристаллич. решётки является рациональным числом, то возникшую дополнит. структуру наз. соизмеримой и говорят, напр., о магн. элементарной ячейке. Примером несоизмеримой структуры является решётка вихрей Абрикосова в сверхпроводниках, периоды к-рой определяются напряжённостью внешнего ноля.
С дополнит. жёсткостями часто оказываются связанными дополнит. ветви коллективных возбуждений. Так, в кристаллах наблюдается поперечный звук, отсутствующий в жидкостях, в ферромагнетиках - спиновые волны, в сверхтекучем HeII - второй звук,
Экспериментальные методы. В нек-рых случаях удаётся непосредственно измерить параметр порядка, напр. намагниченность или спонтанную поляризацию. Др. способ дают дифракц. методы - нейтронографич. или рентгенографич. исследования корреляц. ф-ций удельной плотности или магн. момента (см. Нейтронография, Рентгеновский структурный анализ). В случае дальнего порядка нейтроно- или рентгенограммы обнаруживают узкие брэгговские пики, интенсивность к-рых пропорциональна квадрату объёма F образца. В случае же ближнего порядка эти пики "размываются" на ширину, обратно пропорциональную корреляц. радиусу RC, а их интенсивность пропорциональна RCV. B тех же случаях, когда RC велико, различить ближний и дальний порядок становится трудно (см. Нейтронография структурная, Магнитная нейтронография).
Ряд методов, напр. рассеяние света на звуковых и других длинноволновых колебаниях, позволяет обнаружить коллективные колебания и, следовательно, дополнит. жёсткости (см. Комбинационное рассеяние света). С помощью этих методов можно различить дальний и ближний порядок, если есть возможность исследовать коллективные колебания достаточно низких частот, т. к. высокочастотные колебания существуют и в случае ближнего порядка (напр., сдвиговые волны в жидкости).
Лит.: Ландау Л. Д., Лифшиц E. M., Статистическая физика, 3 изд., ч. 1, M., 1976; Френкель Я. И., Кинетическая теория жидкостей, Л., 1975; Паташинский А. 3., Покровский В. Л., Флуктуационная теория фазовых переходов, 2 изд., M., 1982; Лифшиц E. M., Питаевский Л. П., Физическая кинетика, M., 1979.
Д. E. Хмельницкий.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.