- ИНТЕРВАЛ
-
четырёхмерный (интервал), в теории относительности — величина, характеризующая связь между пространств. расстоянием и промежутком времени, разделяющими два события. С матем. точки зрения И. есть «расстояние» между двумя событиями в четырёхмерном пространстве-времени.В специальной (частной) теории относительности квадрат И. (SAB) между двумя событиями А и В равен:sAB=с2(Dt)2-(Dr)2,где Dt и Dr — соотв. пространств. расстояние и промежуток времени между этими событиями.И. между событиями остаётся неизменным при переходе от одной инерциальной системы отсчёта к другой, т. е. инвариантен относительно Лоренца преобразований (тогда как Dr и Dt зависят от выбора системы отсчёта). Если s2AB>0, то И. наз. времен и подобным; в этом случае существует система отсчёта, в к-рой события происходят в одной пространств. точке (Dr=0) и sAB=CDT, т. е. И. равен промежутку времени между событиями в этой системе, умноженному на скорость света. Если s2AB0, то И. наз. пространственноподобным; в этом случае существует система отсчёта, в к-рой события происходят одновременно (Dt=0) и расстояние между ними Dr=isAB. При sAB=0 И. наз. нулевым; в этом случае Dr=сDt всегда, т. е. события в любой системе отсчёта могут быть связаны световым сигналом (см. ОТНОСИТЕЛЬНОСТИ ТЕОРИЯ).В общей теории относительности, рассматривающей искривлённое пространство-время при наличии тяготения, всё сказанное об И. справедливо для бесконечно близких событий (см. ТЯГОТЕНИЕ).
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- ИНТЕРВАЛ
-
четырёхмерный (интервал) в теории относительности - величина, характеризующая связь между пространств, расстоянием и промежутком времени, разделяющим два события. С матем. точки зрения И. есть "расстояние" между двумя событиями в четырёхмерном пространстве-времени. В спец. (частной) теории относительности квадрат И. (sAB )между двумя событиями А и В равен
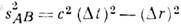 где Dt и Dr - соответственно промежуток времени и пространств, расстояние между этими событиями. И. между событиями остаётся неизменным при переходе от одной инерциалъной системы отсчёта к другой, т. e. инвариантен относительно Лоренца преобразований (тогда как Dr и Dtзависят от выбора системы отсчёта). Если s2AB>0, И. наз. времениподобным; в этом случае существует система отсчёта, в к-рой события происходят в одной пространств, точке (Dr=0) и sAB=cDt, т. е. И. равен промежутку времени между событиями в этой системе, умноженному на скорость света. Если s2AB<0, то И. наз. пространственноподобным; в этом случае существует система отсчёта, в к-рой события происходят одновременно (Dr=0) и расстояние между ними Dr=isAB. При sAB=0 И. наз. нулевым; в этом случае Dr= сDt всегда, т. e. события в любой системе отсчёта могут быть связаны световым сигналом (см. Относительности теория). В общей теории относительности, рассматривающей пространство-время при наличии тяготения, всё сказанное об И. справедливо для бесконечно близких событий (см. Тяготение). И. Д. Новиков.
где Dt и Dr - соответственно промежуток времени и пространств, расстояние между этими событиями. И. между событиями остаётся неизменным при переходе от одной инерциалъной системы отсчёта к другой, т. e. инвариантен относительно Лоренца преобразований (тогда как Dr и Dtзависят от выбора системы отсчёта). Если s2AB>0, И. наз. времениподобным; в этом случае существует система отсчёта, в к-рой события происходят в одной пространств, точке (Dr=0) и sAB=cDt, т. е. И. равен промежутку времени между событиями в этой системе, умноженному на скорость света. Если s2AB<0, то И. наз. пространственноподобным; в этом случае существует система отсчёта, в к-рой события происходят одновременно (Dr=0) и расстояние между ними Dr=isAB. При sAB=0 И. наз. нулевым; в этом случае Dr= сDt всегда, т. e. события в любой системе отсчёта могут быть связаны световым сигналом (см. Относительности теория). В общей теории относительности, рассматривающей пространство-время при наличии тяготения, всё сказанное об И. справедливо для бесконечно близких событий (см. Тяготение). И. Д. Новиков.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.