- ПРОСТРАНСТВО
-
- веществ. линейное пространство, снабжённое не положительно определённым скалярным произведением (а, b). Для П. п. размерности n и индекса p аксиома положит. определённости скалярного произведения евклидова пространства заменяется следующей: существуют п векторов = 1, ..., n, таких, что
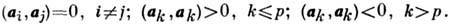
Пара чисел ( р, q), где q = n- p, наз. сигнатурой П. п., обозначаемого
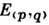 (или).
(или). 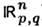 Для физики особенно важно Минковского пространство - время
Для физики особенно важно Минковского пространство - время 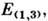 фигурирующее в специальной теории относительности.
фигурирующее в специальной теории относительности.В П. п. можно ввести основные операции векторного и тензорного анализа, в частности индефинитную метрику. Координаты, в к-рых метрич. тензор gij имеет вид
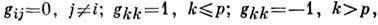
наз. псевдоевклидовыми. В них скалярное произведение принимает вид
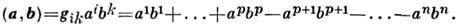
Псевдоевклидов квадрат длины вектора в П. п., в отличие от евклидова, может быть отрицательным, а также нулевым (изотропные векторы). Совокупность изотропных векторов образует изотропный конус.
Движения П. и. образуют п(п+ 1)/2-мерную группу (для E(1,3)- Пуанкаре группу )и в псевдоевклидовых координатах записываются в виде
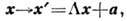
где а- вектор трансляции,
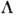 - n
- n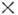 n -матрица поворотов, такая, что
n -матрица поворотов, такая, что 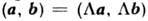 . Метрику П. п. можно получить из метрики евклидова пространства формальной заменой:
. Метрику П. п. можно получить из метрики евклидова пространства формальной заменой: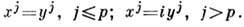
Кривизны тензор П. п. тождественно равен нулю: как и евклидово, оно плоское.
Лит.: Ефимов Н. В., Высшая геометрия, 6 изд., М., 1978; Дубровин Б. А., Новиков С. П., Фоменко А. Т., Современная геометрия, 2 изд., М., 1986; Новиков С. П., Фоменко А. Т., Элементы дифференциальной геометрии и топологии, М., 1987. А. М. Маломестное.,
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.