- МНОЖЕСТВО
-
- набор, совокупность, собрание к.-л. объектов, называемых его элементами, обладающих общим для всех них характеристич. свойством. Понятие M. принадлежит к числу первоначальных матем. понятий и может быть пояснено только при помощи примеров. Так, можно говорить о M. людей, живущих на нашей планете в данный момент времени, о M. точек данной геом. фигуры, о M. решений данного дифференц. ур-ния. Люди, живущие на нашей планете в данный момент времени, точки данной геом. фигуры, решение данного дифференц. ур-ния являются элементами соответствующего M. Множество А считается заданным, если указано характеристич. свойство элементов этого M., т. е. такое свойство, к-рым обладают все элементы этого M., и только они. Для обозначения того, что элемент а принадлежит M. А , пишут а
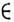 А (если а не принадлежит А, то пишут a
А (если а не принадлежит А, то пишут a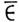 А). Может случиться, что характеристич. свойством, определяющим M. А, не обладает вообще ни один элемент, тогда говорят, что M. А пустое, и пишут А =
А). Может случиться, что характеристич. свойством, определяющим M. А, не обладает вообще ни один элемент, тогда говорят, что M. А пустое, и пишут А =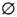 . Напр., M. действительных решений ур-ния х2 = -1 пустое. Если каждый элемент M. А является в то же время элементом M. В, то А наз. подмножеством В и пишут А
. Напр., M. действительных решений ур-ния х2 = -1 пустое. Если каждый элемент M. А является в то же время элементом M. В, то А наз. подмножеством В и пишут А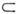 В. Если одновременно выполнено А
В. Если одновременно выполнено А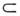 В и В
В и В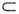 А, то говорят, что M. А и В равны и пишут A = B. Объединением А
А, то говорят, что M. А и В равны и пишут A = B. Объединением А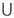 В M. А и В наз. M., состоящее из всех элементов, принадлежащих хотя бы одному из M. А и В. Пересечением А
В M. А и В наз. M., состоящее из всех элементов, принадлежащих хотя бы одному из M. А и В. Пересечением А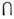 ВM. А и В наз. M., состоящее из всех элементов, принадлежащих как А, так и В. Операции объединения и пересечения коммутативны, ассоциативны и взаимно дистрибутивны. Напр., ( А
ВM. А и В наз. M., состоящее из всех элементов, принадлежащих как А, так и В. Операции объединения и пересечения коммутативны, ассоциативны и взаимно дистрибутивны. Напр., ( А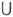 В)
В)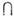 C = = (А
C = = (А 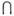 С)
С) 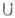 (В
(В 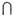 С). Наряду с данными двумя M. А и В рассмотрим M. С, элементами к-рого являются всевозможные пары (а, 6), где а
С). Наряду с данными двумя M. А и В рассмотрим M. С, элементами к-рого являются всевозможные пары (а, 6), где а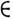 А, b
А, b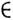 В.M. всех таких пар наз. произведением M. A и B иобозначается А
В.M. всех таких пар наз. произведением M. A и B иобозначается А В. Напр., евклидова плоскость R2=- R1
В. Напр., евклидова плоскость R2=- R1 R1 является произведением двух веществ. прямых R1. Если каждому элементу а
R1 является произведением двух веществ. прямых R1. Если каждому элементу а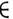 А поставлен в соответствие нек-рый элемент f( а)
А поставлен в соответствие нек-рый элемент f( а) 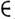 В, то говорят, что задано отображение M. А в M. В (записывается f: А
В, то говорят, что задано отображение M. А в M. В (записывается f: А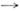 В), иназывают точку f(A )образом точки а при отображении f, M. f(A) - образом M. A, a M. f-1(b) - прообразом точки b
В), иназывают точку f(A )образом точки а при отображении f, M. f(A) - образом M. A, a M. f-1(b) - прообразом точки b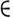 В. Если f(A) - С
В. Если f(A) - С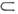 В, то f наз. отображением "в", в случае, когда f(A) = В, f наз. сюрьективным отображение м или отображением "на". Отображение f: А
В, то f наз. отображением "в", в случае, когда f(A) = В, f наз. сюрьективным отображение м или отображением "на". Отображение f: А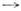 В наз. инъективным или вложением, если из a1, a2
В наз. инъективным или вложением, если из a1, a2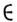 А и a1
А и a1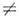 a2 следует f(a1)
a2 следует f(a1) 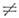 f(a2). Отображения, одновременно инъективные и суръективные, наз. биекциям и или взаимнооднозначными соответствиями.
f(a2). Отображения, одновременно инъективные и суръективные, наз. биекциям и или взаимнооднозначными соответствиями.Часто рассматривают только такие M., к-рые содержатся в нек-ром фиксиров. M. X. Если A - подмножество X и P - свойство, характеризующее элементы из A, то пишут А ={ х
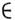 X: Р(х)}, где Р(х )означает, что свойство P выполнено для x (двоеточие заменяет слова "такое, что"). Напр., если X -M. всех действит. чисел, а A - подмножество положит. чисел, то А= { х
X: Р(х)}, где Р(х )означает, что свойство P выполнено для x (двоеточие заменяет слова "такое, что"). Напр., если X -M. всех действит. чисел, а A - подмножество положит. чисел, то А= { х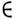 Х: х>0}. Если А
Х: х>0}. Если А X, то M. X А = = {х
X, то M. X А = = {х 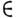 X : c
X : c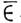 А}. наз. дополнением M. А. Операции объединения, пересечения и дополнения связаны т. н. законами де Моргана, напр.: Х(A
А}. наз. дополнением M. А. Операции объединения, пересечения и дополнения связаны т. н. законами де Моргана, напр.: Х(A  B) = ( Х А)
B) = ( Х А) 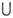 (X В).
(X В).Между двумя конечными M. можно установить биек-цию тогда и только тогда, когда оба M. состоят из одного и того же числа элементов. Обобщая этот факт, Г. Кантор (G. Cantor, 1871-83) определил количественную эквивалентность, или равномощность бесконечных M. как возможность установить между двумя M. взаимно однозначное соответствие. Если M. А равномощно M. В, то говорят, что A и B имеют одно и то же кардинальное число. Ценность понятия мощности M. определяется существованием неравномощных бесконечных M. Напр., M. всех действит. чисел и M. всех натуральных чисел имеют разные мощности. Первое имеет мощность континуума, а второе - счётное M. T. о., бесконечность M. допускает расчленение на разные ступени матем. бесконечности, к-рым соответствуют разл. кардинальные числа, образующие шкалу мощностей. Предположение о месте мощности континуума в этой шкале (точнее, о совпадении континуума с первой несчётной мощностью) наз. континуум-гипотезой. Отметим, что в каждом бесконечном M. А имеется собств. подмножество, равномощное всему А (правильная часть M.), в то время как ни в одном конечном M. такой правильной части найти нельзя. Поэтому наличие правильной части, равномощной целому, можно принять за определение бесконочного M.
Использование теоретико-множеств. конструкций в физике, как правило, опосредованно и происходит в осн. через такие матем. дисциплины, как функциональный анализ, динамич. системы, теория групп, топология, алгебраич. геометрия, нестандартный анализ и др. Классич. пример - формализация дельта-функции Дирака d( х), к-рую физик представляет, напр., как точечную единичную массу бесконечной плотности, а математик - как отображение M. финитных ф-ций на прямую, т. е. функционал на пространстве финитных ф-ций. Др. пример - это моделирование эл.-магн. поля или поля Янга - Миллса как связностей на специальных геом. объектах ( расслоениях), заданных парой пространств E и M и отображением f : E
 M, если M - модель пространства-времени, а f-1( т) - пространство внутр. состояний точки т
M, если M - модель пространства-времени, а f-1( т) - пространство внутр. состояний точки т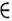 M. Такой подход является существ. шагом в единой теории поля. Многообещающим выглядит использование нестандартного анализа для нового построения квантовой механики и статистич. физики, где формализуются, напр., такие физ. конструкции, как бесконечные флуктуации поля в бесконечно малой области.
M. Такой подход является существ. шагом в единой теории поля. Многообещающим выглядит использование нестандартного анализа для нового построения квантовой механики и статистич. физики, где формализуются, напр., такие физ. конструкции, как бесконечные флуктуации поля в бесконечно малой области.Лит.: Бурбаки H., Начала математики, ч. 1- Основные структуры анализа, кн. 1 - Теория множеств, пер. с франц., M., 1965; Столл P. Р., Множества. Логика. Аксиоматические теории, пер. с англ., M., 1968; Fагrukh M. О., Application of nonstandard analysis to quantum mechanics, "J. Math. Phys.", 1975, v. 16, № 2, p. 177; Александров П. С., Введение в теорию множеств и общую топологию, M., 1977; Mанин Ю. И., Доказуемое и недоказуемое, M., 1979; его же, Калибровочные поля и комплексная геометрия, M., 1984; Девис M., Прикладной нестандартный анализ, пер. с англ., M., 1980; Кантор Г., Труды по теории множеств, пер. с нем., франц., M., 1985; Nonstandard methods in stochastic analysis and mathematical physics, Orlando - [a. o.], 1986; Архангельский А. В., Канторовская теория множеств, М., 1988.
Б. А. Ефимов.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.