- ОПЕРАТОРЫ
-
в квантовой теории, понятие, широко используемое в матем. аппарате квант. механики и квант. теории поля. О. служат для сопоставления с определ. волновой функцией (или вектором состояния) y другой определ. ф-ции (вектора) y'. Соотношение между y и y' записывается в виде y' =L^y, где L ^— О. В квант. механике физ. величинам L (координате, импульсу, энергии и др.) ставятся в соответствие О. L (оператор координаты, импульса и т. д.), действующие на y. Простейшие виды О., действующие на волн. ф-цию y(х) (где х — координата ч-цы),— О. умножения (напр., О. координаты х^, x^y=xy) и О. дифференцирования (напр., О. р^х проекции импульса на ось х, рх^y=-iћдy/дx). Если y — вектор, компоненты к-рого можно представить в виде столбца чисел, то О. представляет собой квадратную таблицу — матрицу.В квант. механике в осн. используются линейные О., к-рые обладают след. св-вом: если L^y1=y'1 и L^y2=y'2, тоL^(с1y1+с2y2)=c1y'1+c2y'2,где c1 и с2 — комплексные числа.Св-ва О. L^ определяются ур-нием L^yn=lnyn, где ln — числа. Решения этого ур-ния yn наз. собственными функциями (собств. векторами) О. ?. Собств. волн. ф-ции (собств. векторы состояния) описывают в квант. механике такие состояния, в к-рых физ. величина L (соответствующая О. ?) имеет определ. значение ln. Числа ln наз. собственными значениями О. L^, а их совокупность — спектром О. Спектр может быть непрерывным или дискретным; в первом случае ур-ние, определяющее yn, имеет решение при любом значении ln (в определ. области), во втором — решения существуют только при определ. дискр. значениях ln. Спектр О. может быть и смешанным: частично непрерывным, частично дискретным. Напр., О. координаты и импульса имеют непрерывный спектр, а О. энергии в зависимости от хар-ра действующих в системе сил — непрерывный, дискретный или смешанный спектр. Дискр. собств. значения О. энергии наз. уровнями энергии.Собств. ф-ции и собств. значения О. физ. величин должны удовлетворять определ. требованиям. Т. к. непосредственно измеряемые физ. величины всегда принимают веществ. значения, то соответствующие квантовомеханич. О. должны иметь веществ. собств. значения. Поскольку при измерении физ. величины в любом состоянии y должно получаться одно из возможных собств. значений О. этой величины, необходимо, чтобы произвольная волн. ф-ция (вектор состояния) могла быть представлена в виде линейной комбинации собств. ф-ций (векторов) yn О. этой физ. величины; другими словами, совокупность собств. ф-ций (векторов) должна представлять полную систему. Этими св-вами обладают собств. ф-ции и собств. значения т. н. самосопряжённых, или эрмитовых, О.С О. можно производить алгебр. действия. В частности, под произведением О. L^1 и L^2 понимается такой О. L^=L^1L^2, действие к-рого на y даёт L^y=y"', если L^2y=y' и L^1y'=y". Произведение О. в общем случае зависит от порядка сомножителей, т. е. L^1L^2?L^2L^1. Этим алгебра О. отличается от обычной алгебры чисел. Возможность перестановки порядка сомножителей в произведении двух О. тесно связана с возможностью физ. системы находиться в состоянии, в к-ром соответствующие О. физ. величины имеют точно определ. Значения (или с возможностью одноврем. измерения физ. величин, к-рым отвечают эти О.). Необходимым и достаточным условием одноврем. измеримости физ. величин L1 и L2 явл. равенство L^1L^2= L^2L^1 (см. ПЕРЕСТАНОВОЧНЫЕ СООТНОШЕНИЯ).Ур-ния квант. механики могут быть формально записаны точно в том же виде, что и ур-ния классич. механики (гейзенберговское представление в квант. механике), если заменить физ. величины, входящие в ур-ния классич. механики, соответствующими им О. Различие между квант. и классич. механикой сведётся тогда к различию алгебр. Поэтому О. в квант. механике иногда наз. q-числами, в отличие от c-чисел, т. е. обыкновенных чисел, с к-рыми имеет дело классич. механика.О. можно также возводить в степень, образовывать из них ряды и рассматривать ф-ции от О. Произведение эрмитовых О. в общем случае не явл. эрмитовым. В квант. механике используются и неэрмитовы О., важным классом к-рых явл. унитарные О., не меняющие норм («длин») векторов и «углов» между ними. Неизменность нормы вектора состояния даёт возможность интерпретации его компонент как амплитуд вероятности и исходной и преобразованной ф-ции. Поэтому действием унитарного О. описывается изменение квантовомеханич. системы с течением времени, а также её смещение как целого в пр-ве, поворот, зеркальное отражение и др. Выполняемые унитарными О. преобразования (унитарные преобразования) играют в квант. механике такую же роль, какую в классич. механике играют канонич. преобразования (см. КАНОНИЧЕСКИЕ УРАВНЕНИЯ МЕХАНИКИ).В квант. механике применяется также О. комплексного сопряжения, не являющийся линейным. Произведение такого О. на унитарный О. наз. антиунитарным О. Антиунитарные О. описывают преобразование обращения времени и некоторые др.В теории квант. систем, состоящих из тождеств. ч-ц, широко применяется метод вторичного квантования. В нём рассматриваются состояния с перем. числом частиц и вводятся О., действие к-рых на вектор состояния с данным числом ч-ц приводит к вектору состояния с изменённым на единицу числом ч-ц (О. рождения и уничтожения ч-ц). О. рождения или уничтожения ч-цы в данной точке х, y^(x), формально подобен волн. ф-ции y(x), как q- и с-числа, отвечающие одной и той же физ. величине соответственно в квант. и классич. механике. Такие О. образуют квантованные поля, играющие фундам. роль в релятив. квант. теориях (квант. электродинамике, теории элем. ч-ц).
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- ОПЕРАТОРЫ
-
в квантовой теории - символич. изображение составленных но определённым правилам матем. операций (алгебраич.,дифференциальных, интегральных, перестановочных и т. д.), используемыхв квантовой теории для преобразования встречающихся в ней величин. Еслисостояние квантовой системы описывается с помощью волновой ф-ции
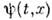 (для конкретности, напр., в Шрёдингера представлении), то О. илиих последовательность в конечном счёте действуют на эту ф-цию, сопоставляяс ней волновую ф-цию, соответствующую уже др. состоянию системы. В др. формализмах квантовой теории (напр., когда состояние системы фиксируетсяс помощью О. матрицы плотности или в представлениях, когда
(для конкретности, напр., в Шрёдингера представлении), то О. илиих последовательность в конечном счёте действуют на эту ф-цию, сопоставляяс ней волновую ф-цию, соответствующую уже др. состоянию системы. В др. формализмах квантовой теории (напр., когда состояние системы фиксируетсяс помощью О. матрицы плотности или в представлениях, когда 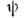 является фиксир. вектором в гильбертовом пространстве )О. действуютна др. О., характеризующие состояние системы или к.-л. её характеристики. Ниже будут рассмотрены наиб. часто встречающиеся типы О.
является фиксир. вектором в гильбертовом пространстве )О. действуютна др. О., характеризующие состояние системы или к.-л. её характеристики. Ниже будут рассмотрены наиб. часто встречающиеся типы О.Операторы динамических величин Общиеположения. В соответствии с осн. принципами квантовой механики (в линейнойотносительно
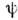 -функции теории) каждой физ. величине F ставится в соответствиелинейный самосопряжённый О.
-функции теории) каждой физ. величине F ставится в соответствиелинейный самосопряжённый О.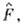 преобразующий
преобразующий 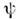 -функциюв новую, но принадлежащую тому же классу ф-цию
-функциюв новую, но принадлежащую тому же классу ф-цию 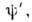
 (где f - число). Если кси задана в виде разложения
(где f - число). Если кси задана в виде разложения 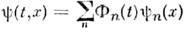
по заранее выбранным базисным ф-циям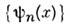 (определяющим конкретное представление как волновой ф-ции, так и действующихна неё О.), т. е. задана как вектор Ф(t) = {Ф п(t)}в бесконечномерном гильбертовом пространстве, то действие 0.
(определяющим конкретное представление как волновой ф-ции, так и действующихна неё О.), т. е. задана как вектор Ф(t) = {Ф п(t)}в бесконечномерном гильбертовом пространстве, то действие 0.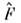 приводит помимо умножения на число f к повороту вектора Ф в этомпространстве, а изменение его компонент Ф п- > Ф' п- к перераспределению квантовомеханич. вероятностей |Ф п(t)|2 обнаружить систему в каждом из состояний, характеризуемых
приводит помимо умножения на число f к повороту вектора Ф в этомпространстве, а изменение его компонент Ф п- > Ф' п- к перераспределению квантовомеханич. вероятностей |Ф п(t)|2 обнаружить систему в каждом из состояний, характеризуемых 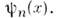 Ф-ции
Ф-ции 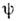 и
и 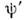 считаютсянормированными на 1, т. е. вне зависимости от наличия штриха
считаютсянормированными на 1, т. е. вне зависимости от наличия штриха 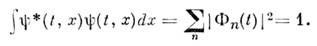
С каждым О.
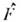 в квантовой механике связывается ур-ние
в квантовой механике связывается ур-ние  определяющее его собств. значения f п и полную системуортонормированных собств. ф-ций
определяющее его собств. значения f п и полную системуортонормированных собств. ф-ций 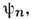 подчинённых определённым граничным и всем необходимым общим для
подчинённых определённым граничным и всем необходимым общим для 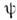 -функцийусловиям. Совокупность величии {f п} определяет спектрвозможных значений физ. величины F, а система ф-ций {
-функцийусловиям. Совокупность величии {f п} определяет спектрвозможных значений физ. величины F, а система ф-ций {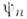 ;(каждая из к-рых характеризует состояние, в к-ром эта величина имеет значение fn )может служить базисом пространства, в к-ром представляются все др. состояниясистемы.
;(каждая из к-рых характеризует состояние, в к-ром эта величина имеет значение fn )может служить базисом пространства, в к-ром представляются все др. состояниясистемы.
Требование линейности О.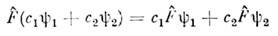
(где
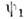 и
и 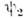 - волновые ф-цни двух возможных состояний системы, c1 и с 2 - числа) можно рассматривать как выражение суперпозициисостояний принципа в квантовой механике, условие же самосопряжённостиоператора
- волновые ф-цни двух возможных состояний системы, c1 и с 2 - числа) можно рассматривать как выражение суперпозициисостояний принципа в квантовой механике, условие же самосопряжённостиоператора 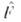 обеспечивает действительность квантовомеханич. ср. значений физ. величины F, к-рыеопределяются как
обеспечивает действительность квантовомеханич. ср. значений физ. величины F, к-рыеопределяются как 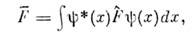
где
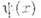 - волновая ф-ция состояния, для к-рого определяется ср. значение F, а
- волновая ф-ция состояния, для к-рого определяется ср. значение F, а 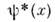 - её комплексносопряжённая величина (если
- её комплексносопряжённая величина (если 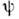 - многокомпонентная ф-ция, то вместо
- многокомпонентная ф-ция, то вместо 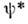 здесь стоит эрмитово сопряжённая ф-ция
здесь стоит эрмитово сопряжённая ф-ция 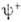 ).Определяя О.
).Определяя О.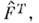 транспонированный по отношению к исходному с помощью соотношения
транспонированный по отношению к исходному с помощью соотношения 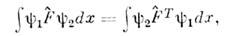
можно записать условие самосопряжённостиО.
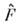 в виде
в виде  где
где 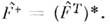 Вслучае, когда система находится в одном из состояний
Вслучае, когда система находится в одном из состояний 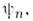 ср. значение
ср. значение 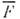 автоматическисовпадает с собств. значением fn. Более того, ур-ние, определяющее собств. ф-ции и собств. значения О.
автоматическисовпадает с собств. значением fn. Более того, ур-ние, определяющее собств. ф-ции и собств. значения О.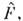 математически эквивалентно обращению в нуль квантовомеханич. дисперсии(не только квадратичной, но и любого порядка) величины F:
математически эквивалентно обращению в нуль квантовомеханич. дисперсии(не только квадратичной, но и любого порядка) величины F: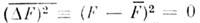 для состояний
для состояний 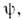 совпадающих с любым из
совпадающих с любым из 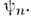 В связи с этим говорят, что в рамках квантовомеханических представленийизмерение физ. величины F может привести только к к.-л. из значений fn.
В связи с этим говорят, что в рамках квантовомеханических представленийизмерение физ. величины F может привести только к к.-л. из значений fn.
Алгебраич. действия с О. определяютсясогласно ф-лам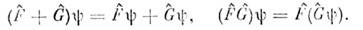
Деление на О. определяется с помощью введенияобратного О.
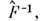 такого, что
такого, что 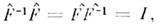 где I означает О. умножения на единицу, причём
где I означает О. умножения на единицу, причём 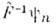 =
=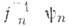 для fn
для fn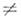 0. Если О.
0. Если О.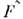 выступает в качестве аргумента нек-рой ф-цни
выступает в качестве аргумента нек-рой ф-цни 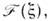 то О.
то О.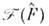 понимаетсякак разложение этой ф-ции в формальный степенной ряд, в к-ром вместо степеней
понимаетсякак разложение этой ф-ции в формальный степенной ряд, в к-ром вместо степеней 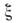 стоятсоответствующие степени О.
стоятсоответствующие степени О.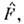
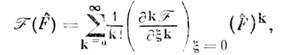
а его собств. значения непосредственновыражаются через собств. значения
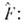
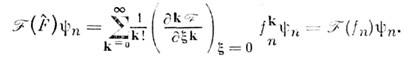
Еслп два О.
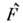 и
и 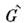 имеютодну и ту же систему собств. ф-ций,
имеютодну и ту же систему собств. ф-ций, и
и  то порядокдействия этих О. в произведении безразличен и коммутатор этих О. равеннулю:
то порядокдействия этих О. в произведении безразличен и коммутатор этих О. равеннулю: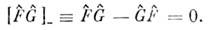
И обратно, величины . и G могутодновременно иметь определённые значения только в том случае, если коммутаторО.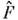 и
и 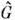 равеннулю. В противном случае физ. величины F и G не могут (врамках квантовой теории) одновременно иметь точные значения. Некоммутативностьряда О. физ. величин приводит к существованию соответствующих неопределённостейсоотношений в квантовой механике. Т. к. при эрмитовом сопряжении произведениядвух О. порядок их расположения меняется,
равеннулю. В противном случае физ. величины F и G не могут (врамках квантовой теории) одновременно иметь точные значения. Некоммутативностьряда О. физ. величин приводит к существованию соответствующих неопределённостейсоотношений в квантовой механике. Т. к. при эрмитовом сопряжении произведениядвух О. порядок их расположения меняется,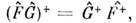 то произведение эрмитовых О. будет также эрмитовым О. только в случае, если эти О. коммутируют друг с другом.
то произведение эрмитовых О. будет также эрмитовым О. только в случае, если эти О. коммутируют друг с другом.
Постановка задачи на полное определениеф-ции состояния и полного набора квантовых чисел п, характеризующихэто состояние, для системы с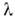 степенями свободы (с обязат. включением степени свободы, связанной с возможнымиэнергетич. состояниями) заключается в построении полного набора независимыхкоммутирующих друг с другом О.
степенями свободы (с обязат. включением степени свободы, связанной с возможнымиэнергетич. состояниями) заключается в построении полного набора независимыхкоммутирующих друг с другом О.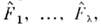 характеризующих положение системы по отношению к её степеням свободы, исовместном решении ур-ний
характеризующих положение системы по отношению к её степеням свободы, исовместном решении ур-ний 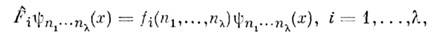
со всеми необходимыми для волновой ф-ции
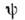 дополнит. условиями, соответствующими характеру рассматриваемой задачи.
дополнит. условиями, соответствующими характеру рассматриваемой задачи.
Конкретное матем. выражение О. дипамич. величины зависит от выбора пространства х, на к-ром определены ф-циисостояния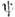 ( х).
( х).
О. в конфигурационном (координатном) представлении. Если волновая ф-цня системы задана как ф-ция пространств, координат и времени,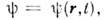 то простейшими О., с помощью к-рых строятся все остальные О. динамич. величин, являются О. координаты
то простейшими О., с помощью к-рых строятся все остальные О. динамич. величин, являются О. координаты 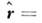
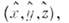 определяемый как умножение на координату
определяемый как умножение на координату  пО. импульса
пО. импульса 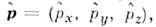 являющийся дифференц. О. первого порядка:
являющийся дифференц. О. первого порядка:
Собств. ф-ция О. координаты, соответствующаясобств. значению r0, представляет собой дельта-функцию Дирака:
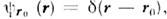 а собств. ф-ция О. импульса, соответствующая собств. значению р,- плоскую волну
а собств. ф-ция О. импульса, соответствующая собств. значению р,- плоскую волну 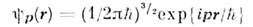
[в обоих случаях нормировка
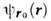 и
и 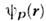 произведенана
произведенана 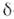 -функцию].О. любой динамич. величины F(p,r )определяется как
-функцию].О. любой динамич. величины F(p,r )определяется как 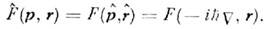
Т. к.
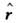 и
и 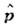 неимеют общей системы собств. ф-ций, то О. дииамич. величин, как правило, нe коммутируют друг с другом, в частности
неимеют общей системы собств. ф-ций, то О. дииамич. величин, как правило, нe коммутируют друг с другом, в частности 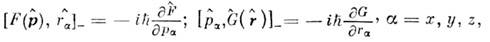
но

Для системы из N частиц динамич. переменные представляются совокупностью координат r1,..., rN и импульсов р1,..., pN и в написанных выше ф-лах аргументы r и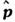 заменяются на r1, ..., rN и
заменяются на r1, ..., rN и 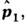 ...,
...,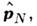 гдекаждое
гдекаждое 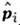 является дифференц. О., действующим на аргумент ri ф-ции
является дифференц. О., действующим на аргумент ri ф-ции 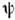 (r1,..., rN).
(r1,..., rN).
Вкачестве примеров для О.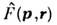 может служить оператор Гамильтона ( гамильтониан)
может служить оператор Гамильтона ( гамильтониан)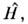 играющийпринципиальную роль во всей квантовой теории и определяющий данную конкретнуюсистему, и О. орбитального (углового) момента
играющийпринципиальную роль во всей квантовой теории и определяющий данную конкретнуюсистему, и О. орбитального (углового) момента 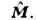 Для N взаимодействующих между собой нерелятивистских частиц гамильтонианимеет вид
Для N взаимодействующих между собой нерелятивистских частиц гамильтонианимеет вид 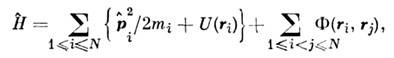
где mi - масса i -йчастицы, U(ri) и Ф(ri,rj)- потенциалы взаимодействия частиц с внеш. полем и друг с другом (еслиэто взаимодействие не зависит от скоростей частиц). Для системы заряж. частиц О. импульса заменяется:
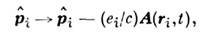
где A(r,t) - векторный потенциалэл.-магн. поля, ei- заряд частицы (в гауссовой системеединиц).
О. момента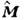 представляетсобой сумму О. моментов для каждой из N частиц. Для одной частицы
представляетсобой сумму О. моментов для каждой из N частиц. Для одной частицы 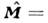
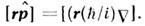 Компоненты О. моменты не коммутируют друг с другом,
Компоненты О. моменты не коммутируют друг с другом,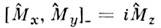 (дведр. лары соотношении получаются при циклич. замене х- > у - x), но
(дведр. лары соотношении получаются при циклич. замене х- > у - x), но 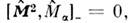 поэтому в квантовой теории имеет смысл говорить о состояниях с определённымизначениями квадрата момента и одной из его компонент, обычно
поэтому в квантовой теории имеет смысл говорить о состояниях с определённымизначениями квадрата момента и одной из его компонент, обычно 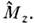 Эти О. как коммутирующие друг с другом имеют общую систему собств. ф-ции [сферическиефункции Yim
Эти О. как коммутирующие друг с другом имеют общую систему собств. ф-ции [сферическиефункции Yim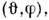 где
где 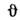 и
и  -угл. переменные сферич. координат] и характеризуются собств. значениями
-угл. переменные сферич. координат] и характеризуются собств. значениями 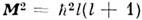 и
и 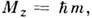 где l =0,1, 2,... и т = - l, - l +1, ..., l - соответственноорбит. и магн. квантовые числа. Если частица движется в центрально-симметричномполе U(r)= U(| r |), то
где l =0,1, 2,... и т = - l, - l +1, ..., l - соответственноорбит. и магн. квантовые числа. Если частица движется в центрально-симметричномполе U(r)= U(| r |), то 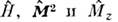 образуют полный набор коммутирующих О. для данной системы с общей системойсобств. ф-ций
образуют полный набор коммутирующих О. для данной системы с общей системойсобств. ф-ций 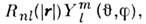 причём l определяет не только величину М2 (и наряду с гл. квантовым числом п энергетич. состояние системы),но и пространственную чётность состояния, характеризующую изменениеволновой ф-ции при инверсии координат,
причём l определяет не только величину М2 (и наряду с гл. квантовым числом п энергетич. состояние системы),но и пространственную чётность состояния, характеризующую изменениеволновой ф-ции при инверсии координат,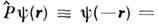
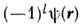 (
(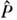 - О. инверсии),т. е. чётность состояния совпадает с чётностью l.
- О. инверсии),т. е. чётность состояния совпадает с чётностью l.Импульсное представление. Если разложить
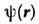 по собств. ф-циям
по собств. ф-циям 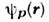 О. импульса:
О. импульса: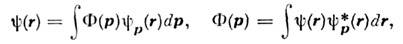
то волновой ф-цией системы в импульсномпредставлении (в к-ром квадрат её модуля определяет распределение плотностивероятности распределения по р )будет её фурье-образ Ф ( р). В соответствии с этим преобразованием О. координаты становится дифференциальным, а О. импульса - О. умножения:
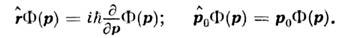
Нормированные на
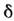 -функциюсобств. ф-ции этих О. имеют вид
-функциюсобств. ф-ции этих О. имеют вид 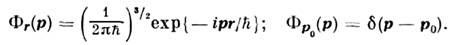
О. динамич. величин
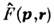 определяются как
определяются как 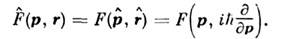
Матричное представление. Рассмотренныевыше представления являются частными случаями, когда в качестве системыбазисных ф-ций {
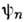 ( х)}выбиралисьсобств. ф-ции координаты или импульса. В общем случае волновая ф-ция системы
( х)}выбиралисьсобств. ф-ции координаты или импульса. В общем случае волновая ф-ция системы 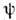 (x,t )можетбыть задана совокупностью компонент Ф(t) = {Ф n(t)} впространстве с достаточно произвольно выбранным базисом {
(x,t )можетбыть задана совокупностью компонент Ф(t) = {Ф n(t)} впространстве с достаточно произвольно выбранным базисом { (t)},
(t)},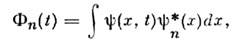
причём величины |Ф n(t)|2 определяют вероятности обнаружить систему в каждом из состояний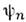 ( х). Представляя
( х). Представляя 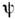 (x,t )ввиде столбца из её компонент {Ф n(0)} [сопряжённую ей- в виде строки из элементов Ф n(t)] а
(x,t )ввиде столбца из её компонент {Ф n(0)} [сопряжённую ей- в виде строки из элементов Ф n(t)] а 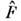 в виде квадратной матрицы
в виде квадратной матрицы 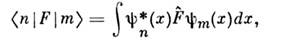
можно записать результат действия этогоО.
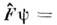
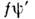 в виде алгебраич. соотношений, определяющих изменённые в результате поворотавектора Ф(t) значения компонент Ф'(t) через их исходные значения:
в виде алгебраич. соотношений, определяющих изменённые в результате поворотавектора Ф(t) значения компонент Ф'(t) через их исходные значения: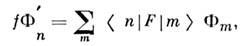
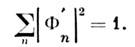
Матричные представления могут быть дискретными, непрерывными (как в случаях координатного и импульсного представления)и смешанного типа, когда часть квантовых чисел, входящих в n, дискретна, часть непрерывна. Приведём неск. общих соотношений в матричном выражении. Алгебраич. действия над О.:
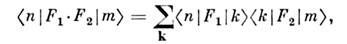
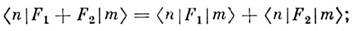
условие самосопряжённости
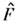 :
: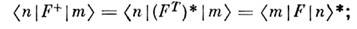
единичный О.
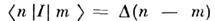 [в случае дискретного спектра
[в случае дискретного спектра 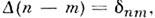 где
где  - Кронекера символ, в случае непрерывного спектра
- Кронекера символ, в случае непрерывного спектра 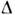 ( п- т)=
( п- т)=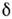 ( п- m), где
( п- m), где 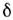 ( п- т) - дираковская
( п- т) - дираковская 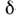 -функция];ф-ла для ср. значений:
-функция];ф-ла для ср. значений: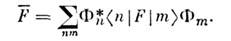
Проблема расчёта собств. значении и собств. ф-ций сводится к решению системы однородных относительно компонент Ф n ур-ний
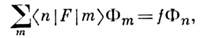
причём условие существования нетривиальногорешения для {Ф n}

является ур-нием (степени, равной рангуматриц, фигурирующих в данном представлении), определяющим спектр собств. значений {fn}.
Если в качестве базиса {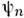 ( х)}выбранасистема собств. ф-ции О.
( х)}выбранасистема собств. ф-ции О.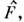 то его матричное представление диагонально,
то его матричное представление диагонально,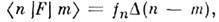 поэтому проблему определения собств. ф-ций и собств. значений нек-рогоО. или неск. коммутирующих друг с другом О. можно представить как проблемуодноврем. диагонализации их матричных представлений.
поэтому проблему определения собств. ф-ций и собств. значений нек-рогоО. или неск. коммутирующих друг с другом О. можно представить как проблемуодноврем. диагонализации их матричных представлений.
Если в качестве базисных ф-ций {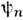 ( х)}используютсясобств. ф-ции оператора Гамильтона,
( х)}используютсясобств. ф-ции оператора Гамильтона,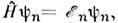 то говорят об энергетич. представлении О. и ф-ций состояния. Однако собств. ф-ции О.
то говорят об энергетич. представлении О. и ф-ций состояния. Однако собств. ф-ции О.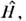 как правило, неизвестны. Поэтому в ряде случаев в качестве системы базисныхф-ций
как правило, неизвестны. Поэтому в ряде случаев в качестве системы базисныхф-ций 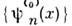 выбирают собств. ф-ции той части
выбирают собств. ф-ции той части 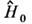 полного гамильтониана
полного гамильтониана 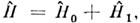 для к-рой удаётся получить точное решение для собств. ф-ций и собств. значений,
для к-рой удаётся получить точное решение для собств. ф-ций и собств. значений,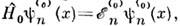 и затем уже в этом матричном представлении развивают теорию возмущенийпо параметру, к-рому пропорц. часть
и затем уже в этом матричном представлении развивают теорию возмущенийпо параметру, к-рому пропорц. часть 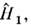 как для расчёта собств. значений
как для расчёта собств. значений 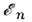 полного
полного 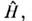 так и его собств. ф-ций.
так и его собств. ф-ций.
Матричное представление является органичнымдля О. момента ввиду дискретности квантовых чисел l и m.Т. к. каждому l соответствует 2l+ 1 значений числа т, тособств. ф-ции О.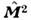 и
и 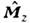 представляютсястолбцами, а О. момента - матрицами (2l+ 1)-ранга, ненулевые элементык-рых определяются ф-лами
представляютсястолбцами, а О. момента - матрицами (2l+ 1)-ранга, ненулевые элементык-рых определяются ф-лами 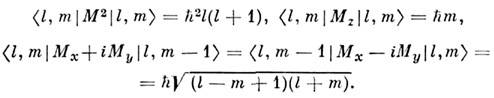
Эти же соотношения справедливы и для О. полного момента
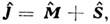 включающего помимо О. орбит, момента
включающего помимо О. орбит, момента 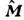 также и О. спина
также и О. спина 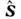 (для к-рого нематричного представления просто не существует), причём квантовоечисло j, заменяющее в этом случае l в приведённых выше ф-лах, принимает ряд целых или полуцелых значении, а число т= - j,-j+ 1,...,j пробегает 2j + 1 значений.
(для к-рого нематричного представления просто не существует), причём квантовоечисло j, заменяющее в этом случае l в приведённых выше ф-лах, принимает ряд целых или полуцелых значении, а число т= - j,-j+ 1,...,j пробегает 2j + 1 значений.
Общие ф-лы для О. момента определяют такжеи О. спинового момента частицы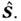 Так, для частиц со cпином 1/2 О. спина
Так, для частиц со cпином 1/2 О. спина 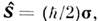 где
где 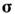 - двухрядные Паули матрицы. Поэтому и состояние электрона (в нерелятивистскойтеории) будет описываться соответственно двухкомпопентной волновой ф-цией[ причём помимо классич. замены в гамильтониане этой системы р-> р - ( е/с) А он должен быть дополнен энергиейвзаимодействия -
- двухрядные Паули матрицы. Поэтому и состояние электрона (в нерелятивистскойтеории) будет описываться соответственно двухкомпопентной волновой ф-цией[ причём помимо классич. замены в гамильтониане этой системы р-> р - ( е/с) А он должен быть дополнен энергиейвзаимодействия -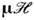 собств. магн. момента электрона
собств. магн. момента электрона 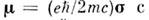 внеш. магн. полем
внеш. магн. полем 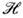 (r,t.)].Врелятивистской теории электрона состояние частицы описывается четырёхкомпонентнойволновой ф-цией (не исключено матричное представление для каждой из них)в соответствии с разл. спиновыми состояниями электрона и состояниями частицаи античастица, а О. выражается четырёхрядными матрицами, элементы к-рыхсами могут быть О. в к.-л. x -представлении. Простейшие примеры полныхнаборов коммутирующих О. для случая свободного движения электрона: гамильтониан
(r,t.)].Врелятивистской теории электрона состояние частицы описывается четырёхкомпонентнойволновой ф-цией (не исключено матричное представление для каждой из них)в соответствии с разл. спиновыми состояниями электрона и состояниями частицаи античастица, а О. выражается четырёхрядными матрицами, элементы к-рыхсами могут быть О. в к.-л. x -представлении. Простейшие примеры полныхнаборов коммутирующих О. для случая свободного движения электрона: гамильтониан 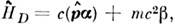 импульс, проекция спина на направление импульса
импульс, проекция спина на направление импульса 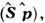 где
где 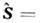
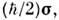 а
а 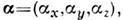
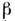 - четырёхрядные Дирака матрицы; или О.
- четырёхрядные Дирака матрицы; или О. D,
D,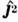 ,
,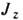 иО. инверсии
иО. инверсии 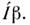 Собств. ф-ции при первом выборе характеризуются плоскими волнами (с импульсомр), проекцией спина s =
Собств. ф-ции при первом выборе характеризуются плоскими волнами (с импульсомр), проекцией спина s =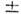 1/2 и энергией
1/2 и энергией 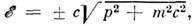 при втором - сферич. волнами, числами j, т и l (чётность).При движении электрона в центрально-симметричном поле U(|r| )системойкоммутирующих О., полностью определяющих состояние системы, являются гамильтониан
при втором - сферич. волнами, числами j, т и l (чётность).При движении электрона в центрально-симметричном поле U(|r| )системойкоммутирующих О., полностью определяющих состояние системы, являются гамильтониан 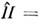
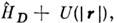 О. квадрата полного момента
О. квадрата полного момента 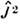 ,его проекции
,его проекции 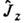 и чётности
и чётности 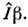 Для частиц со спином 1 необходимо использовать уже как минимум трёхрядныематрицы и т. д.
Для частиц со спином 1 необходимо использовать уже как минимум трёхрядныематрицы и т. д.Представление вторичного квантования эффективно при рассмотрении систем, состоящих из большого числа одинаковыхчастиц (проблема мн. тел в статистич. механике; см. Квантовая теориямногих частиц), или систем, допускающих существование любогочисла частиц одного и того же сорта (см. Квантовая теория поля), иявляется одним из наиб. естеств. способов учёта свойств симметрии волновыхф-ций системы по отношению к перестановкам одинаковых частиц. В основесвоей - это матричное представление, для формулирования к-рого используются N -частичныебазисные ф-ции с определённым типом симметрии
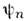 ( х), сконструированныекак симметризов. или аитисимметризов. произведения одночастичных ф-ций
( х), сконструированныекак симметризов. или аитисимметризов. произведения одночастичных ф-ций 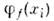 (чаще всего для этого используются известные решения задач на свободноедвижение частицы данного типа), где х = хl, ..., х N,а в наборе квантовых чисел п={...,nf,...} каждоеиз nf указывает, сколько раз в структуре данной базиснойф-ции встречается ф-ция
(чаще всего для этого используются известные решения задач на свободноедвижение частицы данного типа), где х = хl, ..., х N,а в наборе квантовых чисел п={...,nf,...} каждоеиз nf указывает, сколько раз в структуре данной базиснойф-ции встречается ф-ция 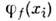 с данным индексом f. Числа nf наз. числамизаполнения (очевидно, а базисные ф-ции обычно обозначают
с данным индексом f. Числа nf наз. числамизаполнения (очевидно, а базисные ф-ции обычно обозначают 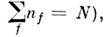 символами
символами 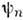 ( х)= |.... nf, ... >, введёнными П. А. М. Дираком (Р.A. М. Dirac), при этом
( х)= |.... nf, ... >, введёнными П. А. М. Дираком (Р.A. М. Dirac), при этом 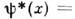
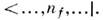 Отличие систем, симметричных и антисимметричных по отношению к перестановкамдвух частиц, проявляется в том, что в первом случае (бозе-частицы) nf могутпринимать любые целые неотрицат. значения, а во втором (ферми-частпцы)- только 0 и 1. Это ограничение на числа заполнения для ферми-систем выражает Паулипринцип. О. динамич. величин, представленные соответствующими матрицами<...nf, ... ... |F| ..., n'f,...>, действуя на волновую ф-цию, имеющую в этом представлении вид векторас компонентами Ф(...,nf ,...), характеризуемыми определённыминаборами чисел nf, "перепутывают" эти наборы. Иными словами, вместо нек-рого Ф(...,nf,...) в результате действия О.F появляется амплитуда Ф(...,nf',...), к-рая характеризуетсяуже другими, изменёнными числами заполнения тех же состояний f,т. е. О. в этом представлении меняют числа частиц в каждом из состоящих f.Удобно рассматривать "элементарные" О., изменяющие на единицу к.-л. изчисел заполнения nf, т. и. О. рождения и О. уничтожениячастицы в состоянии f, и с их помощью выражать более сложные О.F. Действие каждого такого О. рождения и уничтожения меняет на единицуне только определённое число nf, но и общее число частиц N. Т. о., для использования формализма вторичного квантования необходимооперировать с бесконечным набором пространств и соответствующих им базисныхсистем ф-ций [..., nf ,...> для всех значений общегочисла N от нуля до бесконечности. Конкретный результат действия элементарныхО. на эти базисные ф-ции определяется с помощью непосредств. расчёта соответствующихматричных элементов. Действие их на |..., nf,...> вслучае бозе-систем можно представить в виде
Отличие систем, симметричных и антисимметричных по отношению к перестановкамдвух частиц, проявляется в том, что в первом случае (бозе-частицы) nf могутпринимать любые целые неотрицат. значения, а во втором (ферми-частпцы)- только 0 и 1. Это ограничение на числа заполнения для ферми-систем выражает Паулипринцип. О. динамич. величин, представленные соответствующими матрицами<...nf, ... ... |F| ..., n'f,...>, действуя на волновую ф-цию, имеющую в этом представлении вид векторас компонентами Ф(...,nf ,...), характеризуемыми определённыминаборами чисел nf, "перепутывают" эти наборы. Иными словами, вместо нек-рого Ф(...,nf,...) в результате действия О.F появляется амплитуда Ф(...,nf',...), к-рая характеризуетсяуже другими, изменёнными числами заполнения тех же состояний f,т. е. О. в этом представлении меняют числа частиц в каждом из состоящих f.Удобно рассматривать "элементарные" О., изменяющие на единицу к.-л. изчисел заполнения nf, т. и. О. рождения и О. уничтожениячастицы в состоянии f, и с их помощью выражать более сложные О.F. Действие каждого такого О. рождения и уничтожения меняет на единицуне только определённое число nf, но и общее число частиц N. Т. о., для использования формализма вторичного квантования необходимооперировать с бесконечным набором пространств и соответствующих им базисныхсистем ф-ций [..., nf ,...> для всех значений общегочисла N от нуля до бесконечности. Конкретный результат действия элементарныхО. на эти базисные ф-ции определяется с помощью непосредств. расчёта соответствующихматричных элементов. Действие их на |..., nf,...> вслучае бозе-систем можно представить в виде 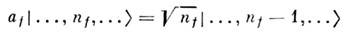
для О. уничтожения af и
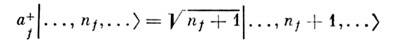
для О. рождения а f+, причем ни а f, ни а f+ недействуют на числа nf', если f '
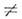 f.Отсюда следуют перестановочные соотношения
f.Отсюда следуют перестановочные соотношения 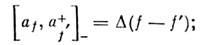
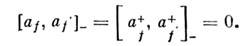
В случае ферми-систем а f и а f+ имеют тот же смысл О. изменения на единицучисла nf, но учёт антисимметрии базисных ф-ций по отношениюк перестановкам индексов частиц и ограничение чисел заполнения двумя значениямиО, 1 приводят к перестановочным соотношениям антикоммутации:
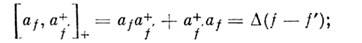
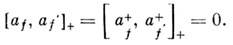
В ряде задач, когда гамильтониан системыцеликом выражается в терминах спиновых О., удобны О. рождения и уничтоженияс коммутац. соотношениями смешанного типа:
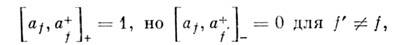
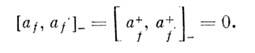
По своей матем. природе они тождественныбозе-O., но действуют в урезанном пространстве чисел заполнения, допускающемзначения nf =0 и nf=1. Их называютпаули - О., т. к. они непосредственно связаны со спиновыми матрицами Паули:
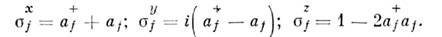
Во всех случаях О. nf = а f+ а f является О. числа частиц в состоянии f и имеетсобств. значения nf= 0, 1, 2, ... для бозе-систем и nf= 0, 1 для ферми- и паули-систем.
Чаще всего в приложениях индекс f означает импульс и спин f = ( р,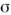 )частицы, т. е. в качестве базисных ф-ций |..., nf,... > выбираютсясимметризов. или антисимметризов. произведения ф-ций
)частицы, т. е. в качестве базисных ф-ций |..., nf,... > выбираютсясимметризов. или антисимметризов. произведения ф-ций 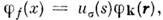 где
где 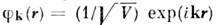 - плоская волна (V - объём
- плоская волна (V - объём системы),
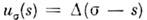 - спиновая ф-ция. Тогда а f+ и af- О. рождения и уничтожения частицы с данным значением импульса и спина. Возможно и "координатное" (или к.-л. иное) представление этих О., определяемоес помощью преобразования типа фурье-преобразования:
- спиновая ф-ция. Тогда а f+ и af- О. рождения и уничтожения частицы с данным значением импульса и спина. Возможно и "координатное" (или к.-л. иное) представление этих О., определяемоес помощью преобразования типа фурье-преобразования: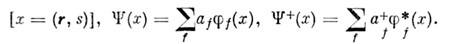
О. дпнамич. величин в представлении вторичногоквантования строятся след. образом: величинам аддитивного динамич. типа, таким, что
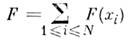 (напр., полный импульс системы из N частиц, их полная кинетич. энергия, энергия взаимодействия с внеш. полем и т. д.) соответствуют О.
(напр., полный импульс системы из N частиц, их полная кинетич. энергия, энергия взаимодействия с внеш. полем и т. д.) соответствуют О.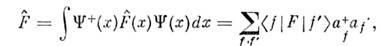
где <f|F|f' > - О.
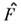 в f -представлении, матричные элементы к-рого рассчитываются с помощьюф-ций
в f -представлении, матричные элементы к-рого рассчитываются с помощьюф-ций 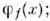 величинамбинарного типа
величинамбинарного типа 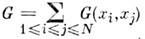 (напр., энергии взаимодействия частиц друг с другом) соответствуют О.
(напр., энергии взаимодействия частиц друг с другом) соответствуют О.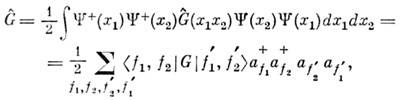
где < f1f2|G|f'1f'2- матричный элемент О.
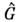 в f -представлении, рассчитанный с помощью системы ф-ций
в f -представлении, рассчитанный с помощью системы ф-ций 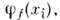 и т. д.
и т. д.
Напр., гамильтониан системы нерелятивистскихчастиц с центр. их взаимодействием Ф(ri,rj)= Ф(ri - rj), находящихсяво внеш. поле U(r), в представлении вторичного квантования имеетвид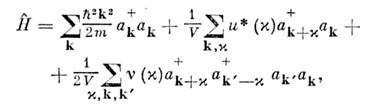
где
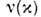 и
и 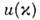 -фурье-образы потенциалов Ф и U, причём для частиц со спином нижнийиндекс у а + и а помимо волнового вектора k включает и спиновый индекс s:
-фурье-образы потенциалов Ф и U, причём для частиц со спином нижнийиндекс у а + и а помимо волнового вектора k включает и спиновый индекс s: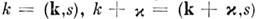 ит. д. Каждое слагаемое этого О. имеет наглядный смысл: общая кинетич. энергияпредставлена как сумма по всем k кинетич. энергий
ит. д. Каждое слагаемое этого О. имеет наглядный смысл: общая кинетич. энергияпредставлена как сумма по всем k кинетич. энергий 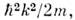 умноженных на числа частиц ak+ak=nk с этой энергией, каждое слагаемое из второйсуммы учитывает рассеяние частицы k - > k +
умноженных на числа частиц ak+ak=nk с этой энергией, каждое слагаемое из второйсуммы учитывает рассеяние частицы k - > k +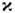 на фурье-компоненте внеш. поля
на фурье-компоненте внеш. поля 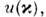 а из третьей суммы - рассеяние двух частиц (k,k') - > (k+ x,k'-
а из третьей суммы - рассеяние двух частиц (k,k') - > (k+ x,k'-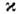 )на фурье-компоненте потенциала их взаимодействия
)на фурье-компоненте потенциала их взаимодействия 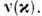
Помимо модели прямого взаимодействия частиц, возможной только в нерелятивистской теории, рассматривается взаимодействиечастиц с разл. полями, переносящими это взаимодействие: в электродинамикес эл.-магн. полем (полем фотонов), в статистич. физике - с полем фононови т. д. В гамильтониан системы в этом случае необходимо добавить свободнуюэнергию этого поля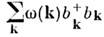 и О. взаимодействия его с частицами системы, имеющий вид
и О. взаимодействия его с частицами системы, имеющий вид 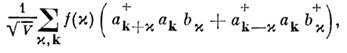
причём элементарный акт этого взаимодействияимеет характер рассеяния частицы с испусканием (или поглощением) квантаполя b. Подобные наглядные представления о взаимодействии послужилиодним из стимулов развития диаграммной техники в квантовой теории поляи в квантовой статистике.
О. энергии и производные О. по времени. В квантовой теории О. энергии определяется как первая производная повремени,
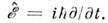 С его помощью записывается ур-ние Шрёдингера - осн. ур-ние квантовой механики, являющееся ур-нием движения для волновой ф-цип,
С его помощью записывается ур-ние Шрёдингера - осн. ур-ние квантовой механики, являющееся ур-нием движения для волновой ф-цип,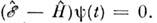 После подстановки
После подстановки 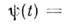
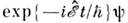 оно превращается в ур-ние на собств. значения гамильтониана,
оно превращается в ур-ние на собств. значения гамильтониана,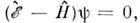 и определяет стационарные состояния системы. О. производной по времени
и определяет стационарные состояния системы. О. производной по времени 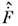 физ. величины F определяется в соответствии с ур-нием движения для
физ. величины F определяется в соответствии с ур-нием движения для 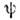 как
как 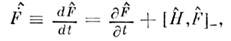
что позволяет определять в квантовой механикеО. величин типа скоростей, ускорений и т. д. Если величина F независит явно от времени и коммутатор
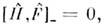 то эта величина является интегралом движения.
то эта величина является интегралом движения.
В релятивистской теории помимо ур-ний, содержащих О.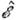 впервой степени, напр. Дирака уравнение
впервой степени, напр. Дирака уравнение 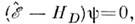 используются ур-ния второго порядка по
используются ур-ния второго порядка по 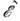 ( Клейна- Гордона уравнение],
( Клейна- Гордона уравнение],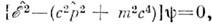 для однокомпонентной
для однокомпонентной 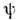 -функциичастицы без спина, а также для векторных 4-компонентных ф-ций и тензорныхболее высокого ранга. Оператор
-функциичастицы без спина, а также для векторных 4-компонентных ф-ций и тензорныхболее высокого ранга. Оператор 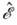 можно рассматривать как нулевую компоненту релятивистского О. энергии-импульса
можно рассматривать как нулевую компоненту релятивистского О. энергии-импульса 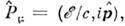
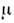 = 0,1,2,3, что позволяет использовать для релятивистских ур-ний удобнуюлоренц-ковариантную запись.
= 0,1,2,3, что позволяет использовать для релятивистских ур-ний удобнуюлоренц-ковариантную запись.
Различные временные представления О. Рассмотреннаявыше схема квантовой теории, когда не зависящей от времени динамич. величине F ставится в соответствие также не зависящий от . О.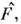 аэволюция системы целиком определяется поведением волновой ф-ции, подчиняющейсяур-нию Шрёдингера, формальное решение к-рого можно представить как
аэволюция системы целиком определяется поведением волновой ф-ции, подчиняющейсяур-нию Шрёдингера, формальное решение к-рого можно представить как 
наз. Шрёдингера представлением дляО. и ф-ций состояния. Из возможных др. временных представлений отметимдва, широко используемых в квантовой теории. В Гейзенберга представлении
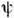 -функцияявляется пост. вектором; полагая в приведённой выше ф-ле t0=0,можно представить эту ф-цию как нач. значение рассмотренной ранее
-функцияявляется пост. вектором; полагая в приведённой выше ф-ле t0=0,можно представить эту ф-цию как нач. значение рассмотренной ранее 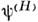 =
=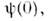 азависимость от t переносится на О. динамич. величин:
азависимость от t переносится на О. динамич. величин: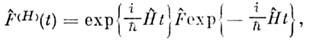 ур-ниедвижения для к-рых имеет вид
ур-ниедвижения для к-рых имеет вид 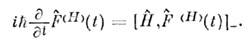
Для построения взаимодействия представление существенно разделение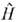 на части,
на части,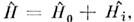 связанное обычно с применением теории возмущений. В атом временном представлениизависимость
связанное обычно с применением теории возмущений. В атом временном представлениизависимость 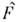 от . определяетсяс помощью нулевого гамильтониана:
от . определяетсяс помощью нулевого гамильтониана: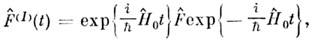 аэволюция волновой ф-ции
аэволюция волновой ф-ции 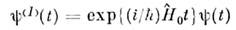 определяется О.
определяется О.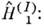
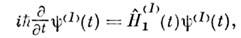
причём формальное решение этого ур-нияможно записать как
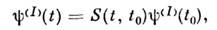
где оператор S -матрицы (наз. матрицейрассеяния)
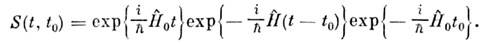
Матрица плотности, матрица рассеянияи другие О.
Наряду с О., непосредственно связаннымис определёнными физ. переменными, в квантовой теории используются О., к-рыеопределяют все свойства системы, включая её состояние, или ряд её свойств. Выше предполагалось, что состояние кваитовомеханич. системы фиксируетсяс помощью волновой ф-ции, представляемой вектором Ф(t) = {Ф n(t)}.Если этому т. н. чистому состоянию поставить в соответствие О.
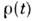 с матричными элементами <n|р| т> = Ф n*(t)Ф m(t),то ср. значения физ. величины F запишутся как
с матричными элементами <n|р| т> = Ф n*(t)Ф m(t),то ср. значения физ. величины F запишутся как 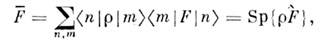
а сам О. p(t) в соответствии с ур-ниемШрёдингера для Ф(t )будет удовлетворять ур-нию
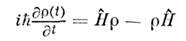
и иметь формальное решение в виде
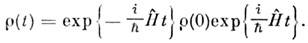
О. р наз. матрицей плотности. Онхарактеризует систему и в случаях, когда она находится в т. н. смешанномсостоянии, что существенно, напр.. при рассмотрении статистич. систем. Матричное представление О. р может быть определено в смешанном представлении(напр., в координатно-импульсном), что невозможно в традиц. квантовой механике, оперирующей с чистыми квантовомеханич. состояниями. О.
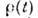 допускает помимо шрёдиигеровского и иные временные представления.
допускает помимо шрёдиигеровского и иные временные представления.
О. S -матрицы (и его модификаций, включая температурные варианты) определяет изменение свойств системы поотношению к нек-рому известному "исходному" состоянию, напр. к состояниюс "выключенным" взаимодействием частиц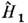 (для этого в
(для этого в 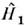 добавляют фактор ехр{ -
добавляют фактор ехр{ -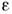 |t|},
|t|},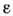 -> 0, обеспечивающий выключение взаимодействия при t - >
-> 0, обеспечивающий выключение взаимодействия при t - >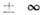 ).Тогда для конечного t (t0- > -
).Тогда для конечного t (t0- > -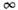 )введённый ранее О. можно представить как бесконечный ряд, записываемыйусловно в виде т. н. Т -экспоненты, т. е. упорядоченного по временнымаргументам (см. Хронологическое произведение )степенного её разложения:
)введённый ранее О. можно представить как бесконечный ряд, записываемыйусловно в виде т. н. Т -экспоненты, т. е. упорядоченного по временнымаргументам (см. Хронологическое произведение )степенного её разложения: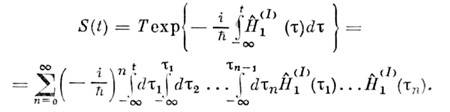
Этот ряд служит основой для построенияприближений в рамках теории возмущений по
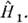
О. t-матрицы, родственной О. S, на простейшем примере задачи двух тел (задачи рассеяния) модифицирует падающуюиз бесконечности на рассеивающий центр H1 = Ф(r )плоскуюволну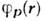 в расходящуюся волну
в расходящуюся волну 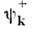 (в соответствии с граничными условиями квантовомеханич. задачи рассеяния),так что
(в соответствии с граничными условиями квантовомеханич. задачи рассеяния),так что 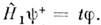 Ур-ние Шрёдингера, записанное в терминах t-О., и его формальное решениеимеют вид
Ур-ние Шрёдингера, записанное в терминах t-О., и его формальное решениеимеют вид 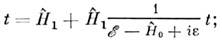
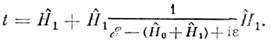
В случаях, когда потенциал Ф(r )не имеет фурье-образа (напр., прп взаимодействии твёрдых сфер конечногорадиуса), а использование импульсного варианта представления вторичногоквантования всё же рационально, импульсное представление t-О. заменяет несуществующуювеличину v(q), причём при малых передачах импульса |q|матричный элемент t-О. выходит на константу, пропорц. длине рассеянияа:
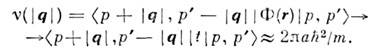
О. преобразований. В квантовой теории такиеО. широко используются для осуществления переходов к др. представлениями координатам, для трансляций и поворотов в разл. пространствах, сдвигаво времени, дискретных преобразований самого разного физ. содержания. Рассмотримнек-рые из них.
Пусть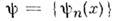 - система базисных ф-ций, определяющих нек-рое n -представление О. и волновых ф-ций, а
- система базисных ф-ций, определяющих нек-рое n -представление О. и волновых ф-ций, а 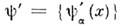 - др. базисная система, соответствующая
- др. базисная система, соответствующая 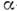 -представлению. Переход от одной системы к другой
-представлению. Переход от одной системы к другой 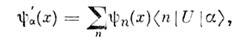
где
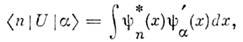 можно символически записать с помощью линейного унитарного О. U, матричноепредставление к-рого приведено выше, как
можно символически записать с помощью линейного унитарного О. U, матричноепредставление к-рого приведено выше, как 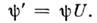 Условие унитарности U+U = I является следствием ортонормироваиностибазисных ф-ций
Условие унитарности U+U = I является следствием ортонормироваиностибазисных ф-ций 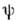 и
и 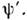 Т. к. обратный О. U-1= U+, тообратное преобразование имеет вид
Т. к. обратный О. U-1= U+, тообратное преобразование имеет вид 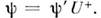 Обозначаясимволом F матричное представление О.
Обозначаясимволом F матричное представление О.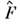 в т -представлепии <n|F|n'> и символом
в т -представлепии <n|F|n'> и символом 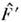 матрицу
матрицу 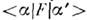 , будем иметь в компактной записи правило преобразования О. динамич. переменнойот одного представления к другому в виде F'= U+FU. Преобразованиеф-ции состояния, определяемой в n -представлении совокупностью компонентФ = {Ф n}, а в
, будем иметь в компактной записи правило преобразования О. динамич. переменнойот одного представления к другому в виде F'= U+FU. Преобразованиеф-ции состояния, определяемой в n -представлении совокупностью компонентФ = {Ф n}, а в 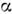 -представлении- совокупностью штрихованных компонент Ф' =
-представлении- совокупностью штрихованных компонент Ф' =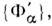 записывается как Ф' = U+ Ф.
записывается как Ф' = U+ Ф.
Унитарные преобразования . сохраняютнормировку волновых ф-ций, свойство их ортогональности, порядок действияО. дниамич. величин, сумму их диагональных элементов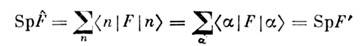
и т. д. Проблему определения собств. значенийО. F можно свести к проблеме построения такого О. U, к-рыйпревращал бы матрицу <n|F|n'> в диагональную:
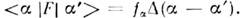
Примеры О. преобразований приводились выше. Так, переход к представлению Гейзенберга осуществлялся с помощью О.
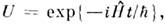 к представлению взаимодействия - с помощью
к представлению взаимодействия - с помощью 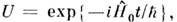 переход от координатного представления к импульсному (в одномерном случае)производится с помощью непрерывной матрицы
переход от координатного представления к импульсному (в одномерном случае)производится с помощью непрерывной матрицы 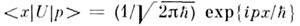 и т. д.
и т. д.
О. U используются при преобразованиисистем координат. При рассмотрении непрерывных преобразований (сдвиг, вращение)достаточно ограничиться бесконечно малым преобразованием данного типа. Напр., О. бесконечно малого смещения координат непосредственноопределяетсяпервыми членами разложения ф-ции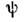 в ряд Тейлора:
в ряд Тейлора: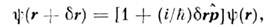
откуда для О. конечной трансляции
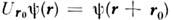 получаем
получаем 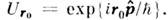 Аиалогичная процедура с бесконечно малым смещением во времени приводитдля конечного сдвига на
Аиалогичная процедура с бесконечно малым смещением во времени приводитдля конечного сдвига на 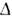 tк известному результату:
tк известному результату: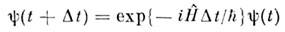
[в представлении взаимодействия
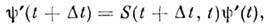 где S(t1,t2) - S -матрица].При бесконечно малом повороте на угол
где S(t1,t2) - S -матрица].При бесконечно малом повороте на угол 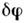 на скалярную ф-цию
на скалярную ф-цию 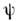 (r )действуетО.
(r )действуетО.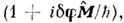 а для частицы со спиом О.
а для частицы со спиом О.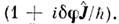
О. конечного поворота, как видно из этихф-л, представляются матрицами (2j + 1)-го ранга. В релятивистскойтеории при бесконечно малых поворотах в четырёхмерном пространстве на угол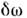 (при Лоренца преобразованиях)
(при Лоренца преобразованиях) О. преобразования ф-ции состояния можно записать как U =1/2
О. преобразования ф-ции состояния можно записать как U =1/2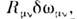 где для четырёхкомпонентной ф-ции фермиона
где для четырёхкомпонентной ф-ции фермиона 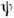 О.
О.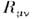 целиком выражается с помощью Дирака матриц
целиком выражается с помощью Дирака матриц 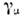 в виде
в виде 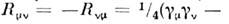
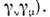
Дискретные преобразования . связаныне только с преобразованиями типа отражений в пространстве и времени, нои с изменением дискретных величин, таких как электрич. заряд, барионноечисло, странность, очарование, цвет и т. д. Приведём примеры О. дискретныхпреобразований, использующихся в теории релятивистских фермн-частиц, к-рыенесложным образом выражаются через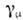 : пространственнаяинверсия (r' -r, х'0= х 0)- U =
: пространственнаяинверсия (r' -r, х'0= х 0)- U =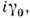 обращение времени (r' - r, х'= - х 0)-U=
обращение времени (r' - r, х'= - х 0)-U=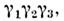 полнаяинверсия (r' - > - r, х' о = -х 0) - U -
полнаяинверсия (r' - > - r, х' о = -х 0) - U -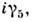 где
где  Возможны и др. законы преобразования ксипри отражениях; напр.,при r' - > - r возможны (помимо упомянутого)ещё три варианта преобразования волновой ф-ции:
Возможны и др. законы преобразования ксипри отражениях; напр.,при r' - > - r возможны (помимо упомянутого)ещё три варианта преобразования волновой ф-ции: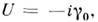 U=
U= (такпреобразующиеся при отражениях
(такпреобразующиеся при отражениях 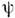 -функцииназ. псевдоспинорами). Аналогичные варианты существуют и для законов преобразованийпри др. отражениях. К дискретным преобразованиям примыкает операция зарядовогосопряжения, имеющая вид
-функцииназ. псевдоспинорами). Аналогичные варианты существуют и для законов преобразованийпри др. отражениях. К дискретным преобразованиям примыкает операция зарядовогосопряжения, имеющая вид 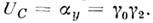
О. перестановок. Такие О. необходимыпри рассмотрении систем двух и более одинаковых частиц. С помощью простейшегоО. перестановки индексов двух частиц
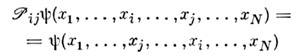
можно построить любой О. перестановки
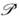 этих индексов, представив его как произведение парных перестановок:
этих индексов, представив его как произведение парных перестановок: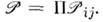 Оператор
Оператор 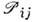 линеен,
линеен,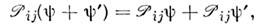
симметричен,
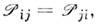 совпадает с обратным,
совпадает с обратным,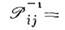
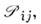 унитарен,
унитарен,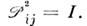 Т. к. в системе одинаковых частиц О. перестановки их индексов не изменяетни О. динамич. величии (в частности, гамильтониана системы
Т. к. в системе одинаковых частиц О. перестановки их индексов не изменяетни О. динамич. величии (в частности, гамильтониана системы 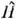 ,т. е.
,т. е.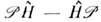 =0), ни граничных и др. дополнит. условий, то волновые ф-ции
=0), ни граничных и др. дополнит. условий, то волновые ф-ции 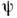 и
и 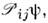 отличающиесярасположением двух индексов частиц у их аргументов, удовлетворяющие однойи той же системе ур-ний и дополнит. условий, описывают одно и то же микроскопия, состояние, т. е.
отличающиесярасположением двух индексов частиц у их аргументов, удовлетворяющие однойи той же системе ур-ний и дополнит. условий, описывают одно и то же микроскопия, состояние, т. е.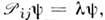 где
где 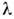 = схр {i
= схр {i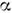 }- фазовый множитель. Повторное применение к этому соотношению О.
}- фазовый множитель. Повторное применение к этому соотношению О.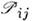 определяет для собств. значения
определяет для собств. значения 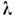 О.
О. условие
условие 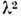 = 1, т. е.
= 1, т. е.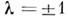 - ф-ция состояния системы одинаковых частиц по отношению к перестановкамих индексов либо симметрична,
- ф-ция состояния системы одинаковых частиц по отношению к перестановкамих индексов либо симметрична,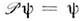 (случай системы бозе-частиц), либо антисимметрична,
(случай системы бозе-частиц), либо антисимметрична,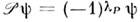 (случай системы ферми-частиц), где
(случай системы ферми-частиц), где 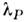 - число парных перестановок
- число парных перестановок 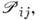 на к-рые распадается данная перестановка
на к-рые распадается данная перестановка 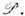 При этом ввиду того, что
При этом ввиду того, что 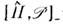 =0, характер симметрии волновой ф-ции является пост. свойством данной системы.
=0, характер симметрии волновой ф-ции является пост. свойством данной системы.
Для двух ферми-частиц О. перестановкиимеет вид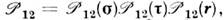 где
где 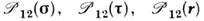 - соответственно О. обмена спинами, зарядами и координатами. Т. к. дляферми-систем
- соответственно О. обмена спинами, зарядами и координатами. Т. к. дляферми-систем 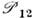 =-1, то для О. перестановки фермионов местами
=-1, то для О. перестановки фермионов местами 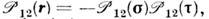
где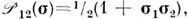
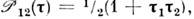
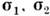 - матрицы Паули, действующие на спиновые переменные каждой из частиц, а
- матрицы Паули, действующие на спиновые переменные каждой из частиц, а 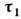 ,
,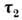 - совпадающие по виду с матрицами Паули операторы изотопического спина.
- совпадающие по виду с матрицами Паули операторы изотопического спина.
О. проектирования вводятся при необходимостивыделить из всего класса допустимых волновых ф-ций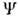 ( х )подпространство ф-ций
( х )подпространство ф-ций 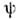 ( х), удовлетворяющихопределённым дополнит. требованиям (напр., подпространство ф-ций с к.-л. дополнит. ограничением на числа заполнения или ф-ций, ортогональных к заданной, и т. д.). Вследствие принципа суперпозиции любую
( х), удовлетворяющихопределённым дополнит. требованиям (напр., подпространство ф-ций с к.-л. дополнит. ограничением на числа заполнения или ф-ций, ортогональных к заданной, и т. д.). Вследствие принципа суперпозиции любую 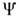 ( х )можнопредставить как
( х )можнопредставить как 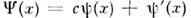 и выделить первое слагаемое с помощью проекционного О.
и выделить первое слагаемое с помощью проекционного О.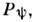 определив его как
определив его как 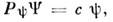 где
где 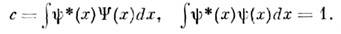
Из свойств
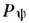 отметим его линейность и свойство
отметим его линейность и свойство 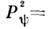
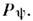 Ввиду отсутствия взаимной однозначности в сопоставлении
Ввиду отсутствия взаимной однозначности в сопоставлении 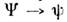 О. проектирования
О. проектирования 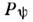 не имеет обратного себе О.
не имеет обратного себе О.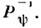 Следует отметить, что О. матрицы плотности
Следует отметить, что О. матрицы плотности 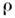 по природе своей является проекционным О. - для чистого состояния Ф, когда <п'
по природе своей является проекционным О. - для чистого состояния Ф, когда <п'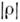 п>==
п>==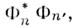 онпросто совпадает с О. проектирования на это состояние: РФ =
онпросто совпадает с О. проектирования на это состояние: РФ =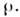
Лит. см. при ст. Квантовая механика, Квантовая теория многих частиц, Квантовая теория поля, Квантовая хромодинамика.
И. А. Квасников.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.