Akademik

механическая (от лат. deformatio - искажение) - изменение взаимного расположения множества частиц материальной среды, к-рое приводит к искажению формы и размеров тела и вызывает изменение сил взаимодействия между частицами, т. е. появление напряжений (см. Напряжение механическое). Д. тела возникает в результате приложения механич. сил, теплового расширения, воздействия электрич. и магн. полей и др. Д. наз. упругой, если она возникает и исчезает одновременно с нагрузкой и не сопровождается рассеянием энергии. Пластическая Д. сохраняется при снятии напряжений и сопровождается рассеянием энергии; величина её зависит не только от значений приложенных сил, но и от предшествующей истории их изменения. Для вязкоупругой Д. типична явная зависимость от процесса нагружения во времени, причём при снятии нагрузки Д. самопроизвольно стремится к нулю.

В кристаллах упругая Д. проявляется в изменении расстояний между узлами и перекосе кристаллич. решётки без изменения порядка расположения атомов; первонач. конфигурация восстанавливается при снятии нагрузки (см. Упругость). Одними из механизмов пластич. Д. в кристалле являются движение и размножение дислокаций. При малых напряжениях перемещение дислокаций обратимо. При напряжениях выше предела упругости движение дислокаций вызывает необратимую перестройку кристаллич. структуры, т. е. Д. становится пластической (см. Пластичность кри сталлов). В поликристаллич. теле (напр., в техн. металле), как правило, одна часть зёрен деформируется упруго, другая - пластически. При этом в макромасштабе необратимая Д. может оказаться ничтожно малой (и тело считается упругим), но её наличие проявляется в т. н. гистерезисе упругом (в частности, свободные колебания затухают вследствие рассеяния энергии, затрачиваемой на пластич. Д. множества зёрен). Для возникновения движения и размножения дислокаций требуется определ. время. С этим связана динамич. чувствительность материала: чем быстрее возрастает нагрузка, тем меньшая пластич. Д. возникает при определ. величине напряжения. Если напряжения, превышающие предел упругости, действуют кратковременно, то движение и размножение дислокаций не успевают развиться и пластич. Д. не возникает (см. Запаздывание текучести). Д. ползучести связана с движением дислокаций, диффузией внедрённых атомов, перестройкой межзёренных связей.

В полимерах Д. определяется изменением конфигурации длинных полимерных цепей и поперечных связей между ними. Наличие дальних взаимодействий обусловливает протяжённость во времени развития Д. Для полимеров типична вязкоупругая Д. (см. Вязкоупругость).

В механике сплошной среды рассматриваются Д. бесконечно малой окрестности точки, по к-рым воспроизводится Д. тел произвольных форм и размеров. Волокном наз. линия, состоящая из частиц вещества. Относительным удлинением e волокна наз. отношение изменения его длины l-l₀ к первонач. длине l₀, т. е. 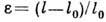. Сдвигом наз. изменение угла между элементарными (бесконечно малыми) волокнами, исходящими из одной точки среды и взаимно перпендикулярными до Д. В точке (её окрестности) Д. определена, если известны относит. удлинения бесчисленного множества элементарных (бесконечно малых) волокон, содержащих эту точку, и изменения углов между ними. Д. наз. малой при 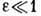(практически - до величин порядка 5-7%).

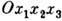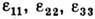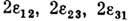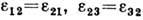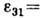
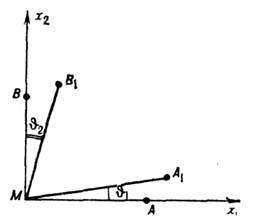
Относит. удлинения элементарных волокон, содержащих рассматриваемую точку M и направленных до Д. параллельно осям прямоуг. системы координат , при малой Д. обозначаются , а сдвиги между ними -, причём ,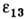. Если MA и MB (рис.) - координатные материальные отрезки до деформации и MА₁ и MB₁ - их положения после деформации, то 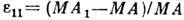, , 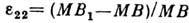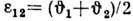. Шесть величин 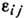образуют тензор малой Д., к-рый полностью определяет Д. окрестности точки M. Напр., относит. удлинение волокна, направление к-рого 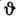образует углы 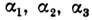с осями 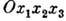, равно

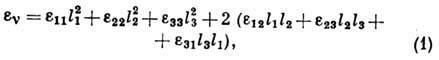
где 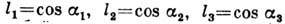. Относит. изменение объёма окрестности точки 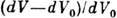равно 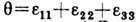. Величина 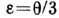наз. средней (гидростатич.) Д. окрестности точки. Тензор Д. можно представить в виде суммы шарового тензора и девиатора. Шаровой тензор Д. определяется величинами

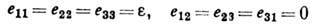
и характеризует объёмную Д. (расширения - сжатия), которую относят к упругой. Величины 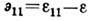, 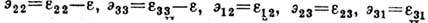определяют девиатор Д., который характеризует Д. изменения формы (сдвига), но не объёма. Такое представление удобно в связи с различием поведения материала при гидростатическом расширении-сжатии и сдвиге. В теории пластичности процесс девиаторной Д. играет особую роль; её изображают кривой - т. н. траекторией Д. Важными характеристиками траектории Д. являются её кривизны.

Шесть ф-ций 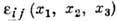определяют деформиров. состояние тела. Если 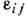не зависят от координат, Д. тела наз. однородной. T. к. величины 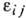связаны с удлинениями и поворотами координатных волокон, то их значения зависят от выбора системы координат. Напр., относит. удлинение 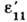волокна, совпадающего до Д. с направлением оси 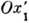системы 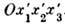, вычисляется по ф-ле (1), если в ней 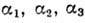- углы между 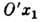и осями 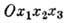. При этом величины

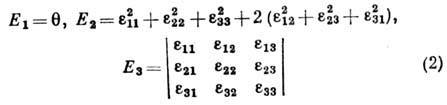
не изменяются при повороте системы координат и наз. инвариантами тензора Д. В каждой точке среды существует три таких взаимно перпендикулярных волокна, что углы между ними при Д. оетаются прямыми. Их относит. удлинения 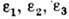наз. главными удлинениями или главными Д., а их направления - главными осями Д. в точке. Главные удлинения также являются инвариантами тензора Д., причём

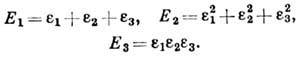
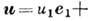
Компоненты тензора малой Д. выражаются через координаты вектора перемещения точки 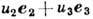( 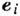-единичные векторы вдоль координатных осей) ф-лами

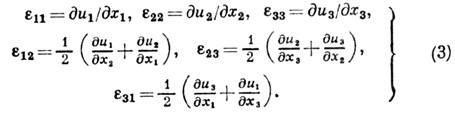
Требование сохранения сплошности тела при Д. налагает на ф-ции 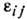определ. ограничения, выражаемые ур-ниями совместности Д. Девять величин 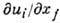, входящих в равенства (3), образуют тензор дисторсии, к-рый определяет не только Д. окрестности точки, но и её поворот.

Иногда удобно рассматривать вектор скорости частицы среды 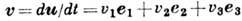, где 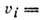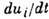, и тензор скоростей Д. 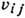, к-рый определяется ф-лами, аналогичными (3), где u_i заменены на v_i.

Компоненты конечной (большой) Д. уже не могут рассматриваться как относит. удлинения и изменения первоначально прямых углов. Количественную меру конечной Д. определяет изменение геометрич. характеристик системы координат, к-рая как бы вморожена в среду и деформируется вместе с ней.

В декартовой системе координат компоненты тензора конечной Д. выражаются через перемещения точек среды ф-лами

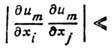
При малых деформациях малые величины 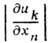отбрасываются и получаются ф-лы (3).

Иногда в качестве меры конечной Д. вводят логарифмич. Д. .

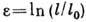Измерения Д. (механические, электрические, магнитные и др.) основаны на прямом или косвенном измерении расстояний между фиксиров. точками тела или порождаемых Д. эффектов (оптических, пьезоэлектрических и т. п.). Количественные характеристики Д. являются существ. параметрами термомеханич. состояния вещества и используются в расчётах прочностных характеристик конструкций, усилий и течения вещества при обработке металлов давлением и др.

Лит.: Ильюшин А. А., Ленский В. С., Сопротивление материалов, M., 1959; Седов Л. И., Механика сплошной среды, 4 изд., т. 1, M., 1983; Ильюшин А. А., Механика сплошной среды, 2 изд., M., 1978. В. С. Ленский.