- СИММЕТРИЯ
-
(от греч. symmetria — соразмерность) законов физики. Если законы, устанавливающие соотношение между величинами, характеризующими физ. систему, или определяющие изменение этих величин со временем, не меняются при определённых операциях (преобразованиях), к-рым может быть подвергнута система, то говорят, что эти законы обладают С. (или инвариантны) относительно данных преобразований. В матем. отношении преобразования С. составляют группу. Опыт показывает, что физ. законы симметричны относительно след. наиб. общих преобразований.Непрерывные преобразования пространства-времени1) Перенос (сдвиг) системы как целого в пространстве. Это и последующие пространственно-временные преобразования можно понимать в двух смыслах: как активное преобразование — реальный перенос физ. системы относительно выбранной системы отсчёта или как пассивное преобразование -параллельный перенос системы отсчёта. С. физ. законов относительно сдвигов в пр-ве означает эквивалентность всех точек пр-ва, т. е. отсутствие в нём выдел. точек (однородность пр-ва).2) Поворот системы как целого в пространстве. С. физ. законов относительно этого преобразования означает эквивалентность всех направлений в пр-ве (изотропию пр-ва).3) Изменение начала отсчёта времени (сдвиг во времени). С. относительно этого преобразования означает, что физ. законы не меняются со временем.4) Переход к системе отсчёта, движущейся относительно данной системы с постоянной (по направлению и величине) скоростью. С. относительно этого преобразования означает, в частности, эквивалентность всех инерциальных систем отсчёта.Все указанные С. отражают псевдоевклидову геометрию четырёхмерного Минковского пространства-времени.Дискретные преобразования пространства-времени.Создание релятив. квант. теории привело к открытию нового типа С., являющейся, в отличие от перечисл. выше, дискретной С. Это — С. законов природы относительно одноврем. проведения преобразований пространственной инверсии (Р), обращения времени (Т) и зарядового сопряжения (С) — замены ч-ц на соответствующие античастицы (см. ТЕОРЕМА СРТ). Существование СРТ-симметрии явл. следствием релятивистской инвариантности и локальности физ. вз-ствий. Относительно отд. дискретных преобразований С, Р и Т оказываются симметричными процессы, обусловленные сильными и эл.-магн. вз-ствиями. В процессах слабого вз-ствия нарушается С. относительно пространств. инверсии и зарядового сопряжения, однако сохраняется С. относительно преобразования комбинированной инверсии (СР) и, следовательно, согласно СРТ-теореме, относительно обращения времени (Т). Исключением явл. нарушение СР-симметрии в распадах долгоживущих K0L-мезонов (см. К-МЕЗОНЫ), природа к-рой ещё не выяснена.Симметрия относительно перестановки одинаковых частиц.При квантовомеханич. описании систем, содержащих одинаковые ч-цы, эта С. приводит к принципу неразличимости одинаковых ч-ц, к полной их тождественности. Волн. ф-ция системы симметрична относительно перестановки любой пари одинаковых ч-ц с целым спином (т. е. их пространственных и спиновых переменных) и антисимметрична относительно такой перестановки для ч-ц с полуцелым спином. Связь спина и статистики явл. следствием релятив. инвариантности теории и тесно связана с СРТ-теоремой.Внутренние симметрии Изотопическая инвариантность сильного взаимодействия и унитарная SU(3)-симметрия.Сильное вз-ствие симметрично относительно поворотов в особом «изотопическом пр-ве». С матем. точки зрения, изотопич. С. отвечает преобразованиям группы унитарной симметрии SU(2). Одним из проявлений этой С. явл. зарядовая независимость яд. сил (см. ИЗОТОПИЧЕСКАЯ ИНВАРИАНТНОСТЬ). Изотопич. инвариантность не явл. точной С. природы, т. к. она нарушается эл.-магн. вз-ствием ч-ц и различием в массах u- и d-кварков.Изотопич. С. представляет собой часть более широкой приближённой С. сильного взаимодействия — унитарной SU(3)-С., объединяющей в семейства частицы, принадлежащие к различным изотопич. мультиплетам и обладающие разл. значениями странности. Унитарная С. оказывается значительно более нарушенной, чем изотопическая, в связи с тем, что масса странного s-кварка довольно сильно отличается от масс u- и d-кварков. Открытие адронов с ещё более массивными с- и b-кварками указывает на наличие более высокой унитарной С. по типу («аромату») кварков. При достигнутых энергиях эти С. очень сильно нарушены, однако возможно, что при энергиях, отвечающих т. Н. «великому объединению», происходит восстановление С.«Цветовая» симметрия.Согласно совр. представлениям, каждый тип кварка может находиться в трёх разл. состояниях, характеризуемых значениями особого квант. числа — «цвета». Сильное вз-ствие симметрично относительно преобразования «цветов» кварков, к-рые составляют «цветовую» группу SU(3). Предполагается, что «цветовая» SU(3)-С,— точная (её нарушение могло бы приводить к вылетанию отд. кварков из адронов; (см. УДЕРЖАНИЕ ЦВЕТА)).Симметрия между кварками и лептонами.На опыте было замечено, что существует С. между электрослабым взаимодействием кварков и лептонов. Эта С. служит одним из оснований для поисков единой теории слабого, эл.-магн. и сильного вз-ствий («великого объединения»).Суперсимметрия.С., связывающая поля, к-рым отвечают как ч-цы с целыми спинами (бозоны), так и с полуцельными (фермионы). (см. СУПЕРСИММЕТРИЯ) .Калибровочная симметрия.С., отвечающая тому факту, что нек-рые сохраняющиеся физ. величины, обобщённо называемые «зарядами» (напр., электрич. заряд, гиперзаряд, изотопический спин, «цвет»), явл. одновременно источниками полей, переносящих вз-ствия между ч-цами, обладающими данным типом «заряда». Закону сохранения обобщённых «зарядов» отвечает инвариантность лагранжиана системы относительно определённой группы преобразований — калибровочных преобразований — с нек-рыми произвольными параметрами, не зависящими от пространственно-временной точки (глобальная симметрия). Так, закону сохранения электрич. заряда соответствует инвариантность лагранжиана относительно умножения волн. ф-ций заряж. ч-ц (yi) на фазовый множитель: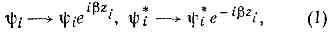 где zi — заряд ч-цы (в ед. элем. электрич. заряда), а b — произвольный числовой множитель. Аналогично сохранение изотопич. спина или «цветового заряда» вытекает из инвариантности лагранжиана относительно группы специальных унитарных преобразований (соответственно SU(2) и SU(3)) с произвольными пост. параметрами. Физ. требование того, чтобы указанные С. выполнялись не только глобально, но и л о к а л ь н о, т. е. для преобразований, параметры к-рых явл. произвольными ф-циями пространственно-временной точки (напр., в (1) b являлся бы произвольной ф-цией координат и времени: b=f(x, у, z, t)l, может быть выполнено при условии, если одновременно определённым образом преобразуются и поля, источниками к-рых служат данные заряды. Возникающие поля оказываются определёнными с точностью до произвольных ф-ций, компенсирующих произвол в выборе локальных параметров преобразования С. Из ур-ний движения следует, что в пространств. отношении эти компенсирующие поля должны быть векторными полями. Требование независимости физ. величин от произвола, с к-рым определены компенсирующие поля, т. е. от калибровки, однозначно приводит к ур-нию движения и законам вз-ствия компенсирующих, или калибровочных, полей. Из этого требования также следует, что масса покоя ч-ц (квантов полей), отвечающих калибровочным полям, должна быть равна нулю. На основе калибровочной С. построены совр. теории электрослабого и сильного вз-ствий (последней явл. квантовая хромодинамика). Для объяснения отличной от нуля массы промежуточных векторных бозонов W± , Z°, являющихся квантами калибровочных полей и выступающих в кач-ве переносчиков короткодействующего слабого вз-ствия, предложен механизм спонтанного нарушения симметрии.Симметрия и законы сохранения.Согласно Нётер теореме, каждому преобразованию С., характеризуемому одним непрерывно изменяющимся параметром, соответствует величина, к-рая сохраняется (не меняется со временем) для системы, обладающей этой С. Из С. физ. законов относительно сдвига замкнутой системы в пр-ве, поворота её как целого и изменения начала отсчёта времени следуют соответственно законы сохранения импульса, момента кол-ва движения и энергии; из С. относительно локальных калибровочных преобразований — законы сохранения зарядов (электрического, гиперзаряда и др.); из изотопич. инвариантности — сохранение изотопич. спина в процессах сильного вз-ствия. Дискр. С. в классич. механике не приводят к к.-л. законам сохранения. Однако в квант. механике, в к-рой состояние системы описывается волн. ф-цией, или для волн. полей (напр., эл.-магн. поля), где справедлив суперпозиции принцип, из существования дискр. С. следуют законы сохранения нек-рых специфич. величин, не имеющих аналогов в классич. механике (напр., пространственной, зарядовой и комбинированной (СР-) чётностей; (см. G-ЧЁТНОСТЬ).Симметрия квантовомеханических систем и вырождение.Если квантовомеханич. система обладает определённой С., то операторы сохраняющихся физ. величин, соответствующих этой С., коммутируют с гамильтонианом системы. Если нек-рые из этих операторов не коммутируют между собой, уровни энергии системы оказываются вырожденными (см. ВЫРОЖДЕНИЕ): определённому уровню энергии отвечает неск. разл. состояний, преобразующихся друг через друга при преобразованиях С. В матем. отношении эти состояния представляют базис неприводимого представления группы С, системы. Это обусловливает плодотворность применения методов теории групп в квант. механике.Помимо вырождения уровней энергии, связанного с явной С. системы (напр., относительно поворотов системы как целого), в ряде задач существует дополнит. вырождение, связанное с т. н. скрытой С. вз-ствия. Такие скрытые С. существуют, напр., для кулоновского вз-ствия и для изотропного осциллятора. Скрытая С. кулоновского вз-ствия, приводящая к вырождению состояний с разл. орбит. моментами, обусловлена явной С. кулоновского вз-ствия в четырёхмерном импульсном пр-ве.Если система, обладающая к.-л. С., находится в поле сил, нарушающих эту С. (но достаточно слабых, чтобы их можно было рассматривать как малое возмущение), происходит расщепление вырожд. уровней энергии исходной системы: разл. состояния, к-рые в силу С. системы имели одинаковую энергию, под действием «несимметричного» возмущения приобретают разл. энергетич. смещения. В случаях, когда возмущающее поле обладает нек-рой С., составляющей часть С. исходной системы, вырождение уровней энергии снимается не полностью: часть уровней остаётся вырожденной в соответствии с С. вз-ствия, «включающего» возмущающее поле.Наличие в системе вырожденных по энергии состояний в свою очередь указывает на существование С. вз-ствия и позволяет в принципе найти эту С., когда она заранее не известна. Последнее обстоятельство играет важнейшую роль, напр., в физике элем. ч-ц.Динамические симметрии.Очень плодотворно понятие т. н. динамической С. системы, к-рое возникает, когда рассматриваются преобразования, включающие переходы между состояниями системы с разл. энергиями. Неприводимым представлением группы динамич. С. будет весь спектр стационарных состояний системы. Понятие динамич. С. можно распространить и на случаи, когда гамильтониан системы зависит явно от времени, причём в одно неприводимое представление динамич. группы С. объединяются в этом случае все состояния квантовомеханич. системы, не являющиеся стационарными (т. е. не обладающие заданной энергией).В определённом смысле к динамич. С. может быть отнесена также киральная симметрия.
где zi — заряд ч-цы (в ед. элем. электрич. заряда), а b — произвольный числовой множитель. Аналогично сохранение изотопич. спина или «цветового заряда» вытекает из инвариантности лагранжиана относительно группы специальных унитарных преобразований (соответственно SU(2) и SU(3)) с произвольными пост. параметрами. Физ. требование того, чтобы указанные С. выполнялись не только глобально, но и л о к а л ь н о, т. е. для преобразований, параметры к-рых явл. произвольными ф-циями пространственно-временной точки (напр., в (1) b являлся бы произвольной ф-цией координат и времени: b=f(x, у, z, t)l, может быть выполнено при условии, если одновременно определённым образом преобразуются и поля, источниками к-рых служат данные заряды. Возникающие поля оказываются определёнными с точностью до произвольных ф-ций, компенсирующих произвол в выборе локальных параметров преобразования С. Из ур-ний движения следует, что в пространств. отношении эти компенсирующие поля должны быть векторными полями. Требование независимости физ. величин от произвола, с к-рым определены компенсирующие поля, т. е. от калибровки, однозначно приводит к ур-нию движения и законам вз-ствия компенсирующих, или калибровочных, полей. Из этого требования также следует, что масса покоя ч-ц (квантов полей), отвечающих калибровочным полям, должна быть равна нулю. На основе калибровочной С. построены совр. теории электрослабого и сильного вз-ствий (последней явл. квантовая хромодинамика). Для объяснения отличной от нуля массы промежуточных векторных бозонов W± , Z°, являющихся квантами калибровочных полей и выступающих в кач-ве переносчиков короткодействующего слабого вз-ствия, предложен механизм спонтанного нарушения симметрии.Симметрия и законы сохранения.Согласно Нётер теореме, каждому преобразованию С., характеризуемому одним непрерывно изменяющимся параметром, соответствует величина, к-рая сохраняется (не меняется со временем) для системы, обладающей этой С. Из С. физ. законов относительно сдвига замкнутой системы в пр-ве, поворота её как целого и изменения начала отсчёта времени следуют соответственно законы сохранения импульса, момента кол-ва движения и энергии; из С. относительно локальных калибровочных преобразований — законы сохранения зарядов (электрического, гиперзаряда и др.); из изотопич. инвариантности — сохранение изотопич. спина в процессах сильного вз-ствия. Дискр. С. в классич. механике не приводят к к.-л. законам сохранения. Однако в квант. механике, в к-рой состояние системы описывается волн. ф-цией, или для волн. полей (напр., эл.-магн. поля), где справедлив суперпозиции принцип, из существования дискр. С. следуют законы сохранения нек-рых специфич. величин, не имеющих аналогов в классич. механике (напр., пространственной, зарядовой и комбинированной (СР-) чётностей; (см. G-ЧЁТНОСТЬ).Симметрия квантовомеханических систем и вырождение.Если квантовомеханич. система обладает определённой С., то операторы сохраняющихся физ. величин, соответствующих этой С., коммутируют с гамильтонианом системы. Если нек-рые из этих операторов не коммутируют между собой, уровни энергии системы оказываются вырожденными (см. ВЫРОЖДЕНИЕ): определённому уровню энергии отвечает неск. разл. состояний, преобразующихся друг через друга при преобразованиях С. В матем. отношении эти состояния представляют базис неприводимого представления группы С, системы. Это обусловливает плодотворность применения методов теории групп в квант. механике.Помимо вырождения уровней энергии, связанного с явной С. системы (напр., относительно поворотов системы как целого), в ряде задач существует дополнит. вырождение, связанное с т. н. скрытой С. вз-ствия. Такие скрытые С. существуют, напр., для кулоновского вз-ствия и для изотропного осциллятора. Скрытая С. кулоновского вз-ствия, приводящая к вырождению состояний с разл. орбит. моментами, обусловлена явной С. кулоновского вз-ствия в четырёхмерном импульсном пр-ве.Если система, обладающая к.-л. С., находится в поле сил, нарушающих эту С. (но достаточно слабых, чтобы их можно было рассматривать как малое возмущение), происходит расщепление вырожд. уровней энергии исходной системы: разл. состояния, к-рые в силу С. системы имели одинаковую энергию, под действием «несимметричного» возмущения приобретают разл. энергетич. смещения. В случаях, когда возмущающее поле обладает нек-рой С., составляющей часть С. исходной системы, вырождение уровней энергии снимается не полностью: часть уровней остаётся вырожденной в соответствии с С. вз-ствия, «включающего» возмущающее поле.Наличие в системе вырожденных по энергии состояний в свою очередь указывает на существование С. вз-ствия и позволяет в принципе найти эту С., когда она заранее не известна. Последнее обстоятельство играет важнейшую роль, напр., в физике элем. ч-ц.Динамические симметрии.Очень плодотворно понятие т. н. динамической С. системы, к-рое возникает, когда рассматриваются преобразования, включающие переходы между состояниями системы с разл. энергиями. Неприводимым представлением группы динамич. С. будет весь спектр стационарных состояний системы. Понятие динамич. С. можно распространить и на случаи, когда гамильтониан системы зависит явно от времени, причём в одно неприводимое представление динамич. группы С. объединяются в этом случае все состояния квантовомеханич. системы, не являющиеся стационарными (т. е. не обладающие заданной энергией).В определённом смысле к динамич. С. может быть отнесена также киральная симметрия.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- СИММЕТРИЯ
-
в физике. В том случае, когда состояние системыне меняется в результате к.-л. преобразования, к-рому она может быть подвергнута, говорят, что система обладает С. относительно данного преобразования. С. физ. системы определяется С. её Гамильтона функции или (в квантовоймеханике) её гамильтонианом, т. е. преобразованиями С. для физ. системы являются преобразования, не меняющие её гамильтониана. В математикетакие преобразования составляют группу. Фундам. значение С. в физикеопределяется прежде всего тем, что каждому непрерывному преобразованиюС. отвечает сохранения закон нек-рой физ. величины, связанной суказанной С. (см. Нётер теорема). Т. о., само существование сохраняющихсяфиз. величин обусловлено определёнными типами С., а физ. величины выступаютв качестве генераторов соответствующих преобразований.
С др. стороны, осн. принцип совр. калибровочных теорий фундам. взаимодействийприроды (напр., сильного и электрослабого), заключающийся в том, что вкачестве источников калибровочных полей - переносчиков взаимодействия -выступают определённые сохраняющиеся величины, играющие тем самым роль«зарядов», может быть реализован только при наличии вполне определённыхлокальных С. Существование такого рода С. однозначно определяет ур-ния, описывающие поведение калибровочных полей. Т. о., симметрия взаимодействийв этом случае полностью определяет их динамику. Подобный подход может бытьиспользован и в теории гравитации. Поэтому соображения о С. взаимодействийлежат в основе попыток построения единой теории всех сил природы (см. Великоеобъединение).
Спец. вопросом является теория С. молекул и кристаллов, к-рая, используятеоретико-групповые методы, устанавливает классы симметрии кристаллов, типы симметрии молекул, классификацию их термов, возможность переходовмежду ними и т. д. На основе теории С. даётся описание физ. явлений в средахс определённой С.
Среди разных типов С. различают пространственно-временные С. и внутренниеС.
Пространственно-временные симметрии Пространственно-временные С. являютсянаиб. общими С. природы. Их можно разделить на С., связанные с непрерывнымии дискретными преобразованиями.
К непрерывным преобразованиям относятся следующие.
(1) Перенос (сдвиг) системы как целого в пространстве [пространственно-временныепреобразования (1) - (4) можно понимать в двух смыслах: как активное преобразование- реальный перенос физ. системы относительно выбранной системы отсчёта;как пассивное преобразование - параллельный перенос системы отсчёта]. С. физ. законов относительно сдвигов в пространстве означает эквивалентностьвсех точек пространства, т. е. отсутствие в пространстве к.-л. выделенныхточек (однородность пространства).
(2) Изменение начала отсчёта времени (сдвиг во времени); С. относительноэтого преобразования означает эквивалентность всех моментов времени (однородностьвремени), благодаря к-рой физ. законы не меняются со временем.
(3) Поворот системы как целого в пространстве; С. физ. законов относительноэтого преобразования означает эквивалентность всех направлений в пространстве(изотропию пространства).
(4) Переход к системе отсчёта, движущейся относительно данной системыс постоянной (по направлению и величине) скоростью. С. относительно этогопреобразования означает, в частности, эквивалентность всех инерциальныхсистем отсчёта.
Все указанные С. отражают свойства плоского 4-мерного пространства Минковскогос псевдоевклидовой метрикой (см. Относительности теория). Преобразования(1) и (2) представляют сдвиги, а (3) и (4) - повороты в пространстве Минковского. С. относительно 1 первых двух преобразований приводит к законам сохраненияимпульса и энергии, а С. относительно поворотов - к закону сохранения моментаи равномерному прямолинейному движению центра инерции физ. системы (в инерциальнойсистеме координат).
Это имеет глубокий смысл. Поскольку при всех наблюдениях изучается несамо пространство, а поведение материальных объектов (в т. ч. и распространениесвета), то, по мысли А. Пуанкаре (A. Poincare), не может существовать «абсолютная»геометрия пространства, оторванная от физ. явлений. Геом. аксиомы, согласноПуанкаре, представляют собой условные положения (соглашения), при выборек-рых руководствуются лишь опытными фактами, но сам выбор остаётся свободными ограничен только необходимостью избегать внутр. противоречий. Евклидовагеометрия, по мысли Пуанкаре, является предпочтительной, т. к. она прощедругих геометрий и в достаточной степени согласуется со свойствами твёрдыхтел. Однако Пуанкаре упускал связь С. пространства с законами сохранения. Если принять в качестве постулата независимое существование всех перечисленныхвыше законов сохранения, связывающих все возможные процессы в природе (независимоот того, какими силами они вызываются), то 4-мерное пространство Минковскогос псевдоевклидовой метрикой может рассматриваться именно в качестве «абсолютной»геометрии пространства-времени. При этом в пространстве Минковского можетбыть построена и релятивистская теория гравитации, результаты к-рой дляэкспериментально наблюдавшихся в Солнечной системе явлений совпадают свыводами общей теории относительности А. Эйнштейна (A. Einstein)(ОТО). Риманово пространство ОТО с точки зрения этой теории является«эффективным» пространством, к-рое не может иметь сложной топологии, поскольку«кривизна» его связана с универсальным «искривлением» движения материальныхобъектов под действием гравитац. поля в пространстве Минковского. В такойтеории естественно выполняются все законы сохранения и возможна локализацияэнергии - импульса гравитац. поля, не существующая в римановом пространстве(напр., для сильных гравитац. полей).
Дискретные пространственно-временные симметрии. Слабое и сильноеотражение. СРТ- симметрия. Из свойств пространства Минковского иосн. положений квантовой теории поля следует, что для любой частицы, обладающейк.-л. зарядом, должна существовать симметричная ей античастица (обладающаятой же массой, временем жизни и спином, но с противоположным значениемзаряда), а также необходимость определённой С. между движениями частици античастиц. Основой для указанной С. является то, что одноврем. отражениевсех пространственных oceit ( Р )и временной оси ( Т )(т. е. переходк зеркальной системе пространственных координат и отсчет времени в обратномнаправлении) формально сводится к повороту в пространстве Минковского намнимый угол (в евклидовом пространстве чётное число отражений сводитсяк реальному повороту). Поэтому теория, удовлетворяющая требованиям релятивистскойинвариантности, т. е. инвариантная относительно поворотов в пространствеМинковского, должна быть инвариантна и относительно т. н. слабого отражения( РТ). (То, что при этом поворот осуществляется на мнимый угол, не имеет принципиальногозначения, по крайней мере, для теорий с локальным взаимодействием частицс конечным спином.)
Поскольку при слабом отражении энергия и импульс частиц меняются напротивоположные значения, инвариантность теории относительно слабого отражения, казалось бы, приводит к существованию физически недопустимых состоянийс отрицат. энергиями. В квантовой теории поля это можно устранить, истолковавдвижение частиц с отрицат. энергиями как обращённое но времени, зеркальносимметричное движение частиц с положит. энергиями, но с противоположнымзначепнем заряда. Т. о., необходимость существования античастиц следуетиз требования релятивистской инвариантности и положительности энергии.(По. существу из тех же самых требовании вытекает связь спина частиц сих статистикой - см. Паули теорема. )Законы природы оказываются, следовательно, симметричными относительно т. н. сильного отражения ( СРТ), заключающегосяв одноврем. проведении слабого отражения и зарядового сопряжения ( С )(т. е. перехода от частиц к античастицам). Это утверждение составляетсодержание теоремы СРТ, согласно к-рой для любого движения частицможет осуществляться в природе симметричное ему (обращённое по времени, зеркально отражённое) движение античастиц.
Несмотря на то что из общих принципов теории следует С. лишь относительноодноврем. проведения преобразований Р, Т, С, в широком классе явленийсуществует С. по отношению к каждому из указанных преобразований в отдельности.
Зеркальная симметрия (С. относительно инверсии Р). Осуществляетсяв процессах, вызываемых сильными и эл.-магн. взаимодействиями, а такжев системах, связанных с помощью этих взаимодействий (атомах, атомных ядрах, молекулах, кристаллах и т. д.). Наличие зеркальной С. означает, что длялюбого процесса, обусловленного сильным или эл.-магн. взаимодействием, с равной вероятностью могут осуществляться два зеркально-симметричных перехода. Это обусловливает, напр., симметричность относительно плоскости, перпендикулярнойспину, угл. распределения квантов, испускаемых поляризов. ядрами [посколькувероятности вылета
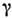 -квантапод углами
-квантапод углами 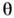 и
и  к спинуядра одинаковы:
к спинуядра одинаковы: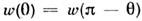 ]. Зеркально-симметричные состояния отличаются друг от друга противоположныминаправлениями скоростей (импульсов) частиц и электрич. полей и имеют одинаковыенаправления магн. полей и спинов частиц. С. гамильтониана относительнопространственной инверсии отвечает закон сохранения пространственной чётностисистемы. Пространственная чётность, подобно др. величинам, существованиек-рых связано с дискретными С., не имеет аналога в классич. механике (т. к. в последней нет понятия относит. фазы между состояниями), однако онаможет служить характеристикой волновых движений (напр., в волноводах).
]. Зеркально-симметричные состояния отличаются друг от друга противоположныминаправлениями скоростей (импульсов) частиц и электрич. полей и имеют одинаковыенаправления магн. полей и спинов частиц. С. гамильтониана относительнопространственной инверсии отвечает закон сохранения пространственной чётностисистемы. Пространственная чётность, подобно др. величинам, существованиек-рых связано с дискретными С., не имеет аналога в классич. механике (т. к. в последней нет понятия относит. фазы между состояниями), однако онаможет служить характеристикой волновых движений (напр., в волноводах).Наличие зеркальной С. гамильтониана взаимодействий не исключает возможностисуществования физ. состояний, где такая С. нарушена. Примером могут служитьизомерные молекулы, к-рые вращают плоскость поляризации света в противоположныестороны. Существование изомерии молекул явно нарушает зеркальнуюС. и представляет собой случай т. н. спонтанного нарушения симметрии. ОбщаяС. гамильтониана относительно инверсий проявляется в том, что для любой, напр. левовращающей, молекулы существует правовращающий изомер, представляющийсобой зеркальное изображение первой. Формальное нарушение зеркальной С. связано, т. о., в этом случае с вырождением осн. состояния и асимметриейфиз. вакуума для света, распространяющегося в веществе из одних правовращающихили левовращающих молекул.
Зарядовая симметрия. Сильные и эл.-магн. взаимодействия инвариантныотносительно операции зарядового сопряжения: замены всех частиц на соответствующиеим античастицы. Эта С. не является пространственной и рассматривается вэтом разделе из-за её связи с СРТ -симметрией. Зарядовая С. приводитк закону сохранения особой величины - зарядовой чётности (или С-чётности),характеризующей истинно нейтральную частицу (или систему частиц, не обладающуюк.-л. зарядом), переходящую сама в себя при зарядовом сопряжении.
СР-симметрия. С. гамильтониана относительно преобразования пространственнойинверсии одновременно с зарядовым сопряжением (комбиниров. инверсия) наз. СР-симметрией. Поскольку сильные и эл.-магн. взаимодействия симметричныотносительно каждого из этих преобразований, они симметричны и относительнокомбиниров. инверсии. Однако относительно этого преобразования оказываютсясимметричными и слабые взаимодействия, к-рые не обладают С. по отношениюк преобразованию инверсии и зарядовому сопряжению в отдельности. С. процессовслабого взаимодействия относительно комбиниров. инверсии может служитьуказанием на то, что отсутствие зеркальной С. в них связано со структуройэлементарных частиц и что античастицы по своей структуре являются как бы«зеркальным изображением» соответствующих частиц. В этом смысле процессыслабого взаимодействия, происходящие с к.-л. частицами, и соответствующиепроцессы с их античастицами связаны между собой так же, как и явления воптич. изомерах.
Открытие распадов долгоживущих
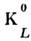 -мезоновна два
-мезоновна два 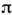 -мезонаи наличие зарядовой асимметрии в распадах
-мезонаи наличие зарядовой асимметрии в распадах 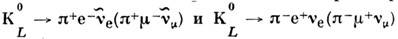 (см.К-мезоны )указывают на существование сил, несимметричныхотносительно комбиниров. инверсии. Пока не установлено, являются ли этисилы малыми добавками к известным фундам. взаимодействиям (сильному, эл.-магн.,слабому) или же имеют особую природу. Возможно, что нарушение СР-симметриисвязано со спонтанным нарушением С. физ. вакуума в нашей области Вселенной.
(см.К-мезоны )указывают на существование сил, несимметричныхотносительно комбиниров. инверсии. Пока не установлено, являются ли этисилы малыми добавками к известным фундам. взаимодействиям (сильному, эл.-магн.,слабому) или же имеют особую природу. Возможно, что нарушение СР-симметриисвязано со спонтанным нарушением С. физ. вакуума в нашей области Вселенной.Симметрия относительно обращения времени ( Т). Благодарясуществованию СРТ- и СР-симметрий как для сильных, так и для электрослабыхвзаимодействий (исключая взаимодействие, нарушающее СР-симметрию) выполняетсяС. относительно обращения времени. Она означает, что любому движению поддействием этих сил соответствует в природе симметричное движение, при к-ромсистема проходит в обратном порядке все состояния, что и в первоначальномдвижении, но с изменёнными на противоположные направлениями скоростей частиц, спинами и магн. полями. Из Т-симметрии следуют соотношения между прямымии обратными реакциями, позволяющие экспериментально проверять выполнениеТ-инвариантности в разл. процессах (см. Деталгмого равновесия принцип), а также ряд др. заключений (см., напр., Крамерса теорема).
Симметрия относительно перестановки одинаковых частиц. При квантовомеханич. описании систем, содержа щих одинаковые частицы, эта С. приводит к принципунеразличимости одинаковых частиц, к полной их тождественности. Волноваяф-ция системы симметрична относительно перестановки любой пары одинаковыхчастиц с целым спином (т. е. перестановки их пространственных и спиновыхпеременных) и антисимметрична относительно такой перестановки для частицс полуцелым спином. Связь спина и статистики является следствием релятивистскойинвариантности теории и тесно связана с СРТ-теоремой.
Симметрия (или антисимметрия) волновой ф-ции относительно перестановкиодинаковых частиц является простейшим (одномерным) представлением группы перестановок. В принципе математически возможно существование более сложных (многомерных)представлений этой группы (см. Парастатистика). Реальные более сложныетипы С. возникают отдельно для координатных (или спиновых) волновых ф-цийодинаковых частиц, когда рассматриваются перестановки только координат(или только спинов) одинаковых частиц (см. Юнга схемы).
Внутренние симметрии. Под внутренними С. понимают С. между частицами(в квантовой теории поля - между полями) с различными внутренними квантовымичислами. Среди различных внутр. С. можно выделить глобальные С. и локальныеС.
Глобальные С. Примером такой С. является инвариантность лагранжианаотносительно следующих калибровочных пребразований входящих в негополей:
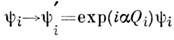 ,
,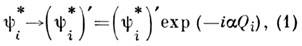
где
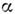 - произвольное число, а числа Qi фиксированы для каждогополя
- произвольное число, а числа Qi фиксированы для каждогополя 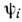 .Эта инвариантность приводит к аддитивному закону сохранения заряда
.Эта инвариантность приводит к аддитивному закону сохранения заряда 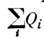 =const. Наряду с электрическим в качестве зарядов могут выступать и др. заряды: барионный, лептонный, странность и т. д. Инвариантность относительнопреобразования (1) выполняется, когда в лагранжиан симметрично в виде комбинации
=const. Наряду с электрическим в качестве зарядов могут выступать и др. заряды: барионный, лептонный, странность и т. д. Инвариантность относительнопреобразования (1) выполняется, когда в лагранжиан симметрично в виде комбинации 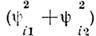 входят два
входят два действительных поля
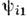 и
и 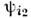 (содинаковыми массами). В этом случае они могут быть заменены комплекснымиполями
(содинаковыми массами). В этом случае они могут быть заменены комплекснымиполями 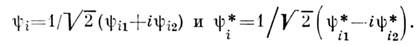
Преобразование (1) отвечает преобразованию «поворота» полей вокруг фиксиров. оси:
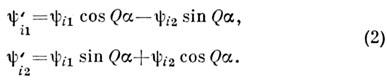
Симметрия (1) наз. глобальной С., если параметр преобразования
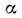 не зависит от пространственно-временных координат точки, в к-рой рассматриваетсяполе. Преобразования (1) с разл. параметрами
не зависит от пространственно-временных координат точки, в к-рой рассматриваетсяполе. Преобразования (1) с разл. параметрами 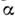 коммутируют между собой и составляют абелеву группу U(1) [см. СимметрияU(1)]. Если лагранжиан симметричен относительно преобразований «поворотов»неск. комплексных полей, то возникают более сложные, неабелевы группы С. с неск. параметрами, напр. группа SU(2 )для изотопического спина[см. Симметрия SU(2)], группа SU(3 )для цветовой С. [SU с(3), см. Цвет, Симметрия SU(3)] или С. между ароматами кварков [SUf(3)]. Во всех случаях С. наз. глобальной, если параметры преобразований независят от пространственно-временных координат.
коммутируют между собой и составляют абелеву группу U(1) [см. СимметрияU(1)]. Если лагранжиан симметричен относительно преобразований «поворотов»неск. комплексных полей, то возникают более сложные, неабелевы группы С. с неск. параметрами, напр. группа SU(2 )для изотопического спина[см. Симметрия SU(2)], группа SU(3 )для цветовой С. [SU с(3), см. Цвет, Симметрия SU(3)] или С. между ароматами кварков [SUf(3)]. Во всех случаях С. наз. глобальной, если параметры преобразований независят от пространственно-временных координат.Дополнительная, т. н. киральная симметрия возникает для частицнулевой массы. Поскольку для безмассовых частиц сохраняется их спиральность, наличиек.-л. внутр. С. для них приводит к тому, что она может выполняться независимодля левых и правых частиц (с положит. и отрицат. спиральностью). Так, для
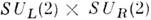 безмассовых и-, d- кварков должна быть группа С.
безмассовых и-, d- кварков должна быть группа С.Локальные С. Если параметры преобразований для глобальных С. можно рассматриватькак произвольные ф-ции пространственно-временных координат, то говорят, что соответствующие С. выполняются локально. Предположение о существованиилокальной С. позволяет построить теорию, в к-рой сохраняющиеся (благодаряналичию глобальной С.) величины (заряды) выступают в качестве источниковособых калибровочных полей, переносящих взаимодействие между частицами, обладающими соответствующими зарядами. Поскольку во всякую динамич. теориювходит обобщённый импульс, оператор к-рого
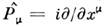 при действии на преобразованное поле приводит в случае локальной С. к появлениюпроизвольных ф-ций [напр.,
при действии на преобразованное поле приводит в случае локальной С. к появлениюпроизвольных ф-ций [напр.,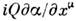 для преобразования (1)], то инвариантность теории возможна лишь при условии, когда возникающий произвол каким-то образом компенсируется. Такая компенсацияоказывается возможной, если обобщённый импульс входит в теорию в комбинациис нек-рым векторным полем, соответственно изменяющимся при калибровочныхпреобразованиях. Т. о., локальная С. может осуществляться только при наличиикомпенсирующих (калибровочных) полей. Для локальной U(1)-симметрииобобщённый импульс должен входить в комбинации
для преобразования (1)], то инвариантность теории возможна лишь при условии, когда возникающий произвол каким-то образом компенсируется. Такая компенсацияоказывается возможной, если обобщённый импульс входит в теорию в комбинациис нек-рым векторным полем, соответственно изменяющимся при калибровочныхпреобразованиях. Т. о., локальная С. может осуществляться только при наличиикомпенсирующих (калибровочных) полей. Для локальной U(1)-симметрииобобщённый импульс должен входить в комбинации 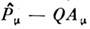 с векторным полем
с векторным полем 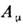 ,к-рое при преобразованиях (1) изменяется по закону
,к-рое при преобразованиях (1) изменяется по закону 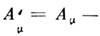
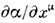
Произвол, существующий в определении поля
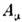 (произвольная ф-ция
(произвольная ф-ция 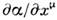 ), устраняется в тензоре
), устраняется в тензоре 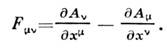 Поэтому физ. величинами являются компоненты тензора
Поэтому физ. величинами являются компоненты тензора 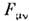 ,из к-рого однозначно строится лагранжиан поля
,из к-рого однозначно строится лагранжиан поля 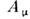
Для локальных неабелевых С. необходимо существование неск. векторныхкалибровочных полей, к-рые в этом случае будут сами обладать «зарядами»и взаимодействовать между собой. Требование отсутствия калибровочного произволав физ. величинах позволяет однозначно установить закон взаимодействия этихполей. Впервые модель с локальной изотопической SU(2)-симметриейбыла рассмотрена Ч. Янгом (Ch. Yang) и Р. Л. Миллсом (R. L. Mills) в 1954.Успех квантовой хромодинамики, построенной на основе локальной цветовой SU с(3)-симметриии теории электрослабых взаимодействий, позволяет предположить, чтотребование локальной С. является общим принципом построения теории фундаментальныхвзаимодействий. Исходя из этих принципов строятся разл. модели Великогообъединения, в к-рых пытаются учесть наблюдаемую в электрослабом взаимодействииС. между лептонами и кварками, С. между разл. поколениями лептонов и кварков, а также использовать предполагаемую суперсимметрию, связывающую частицыс целым и полуцелым спином (см. Суперсимметрия, Супергравитация).
Нарушение симметрии. Многие из С. природы являются приближённымиили нарушенными. Следует различать при этом явное и спонтанное нарушениесимметрии. Явное нарушение С. обусловлено нарушением С. эффективногогамильтониана системы [напр., нарушение изотопич. инвариантности и
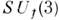 -симметрии по ароматам кварков связано с различием их масс]. Спонтанноенарушение С. происходит из-за нарушения С. вакуума, к-рый при симметричномгамильтониане может быть вырожденным (см. Вырождение вакуума). Спонтанноенарушение глобальных С. приводит к появлению безмассовых (голдстоуновских)частиц (см. Голдстоуна теорема, Голдстоуновские бозоны). Спонтанноенарушение калибровочных С. может, наоборот, приводить к тому, что безмассовыечастицы, отвечающие калибровочным полям (какими являются, напр., поля промежуточных
-симметрии по ароматам кварков связано с различием их масс]. Спонтанноенарушение С. происходит из-за нарушения С. вакуума, к-рый при симметричномгамильтониане может быть вырожденным (см. Вырождение вакуума). Спонтанноенарушение глобальных С. приводит к появлению безмассовых (голдстоуновских)частиц (см. Голдстоуна теорема, Голдстоуновские бозоны). Спонтанноенарушение калибровочных С. может, наоборот, приводить к тому, что безмассовыечастицы, отвечающие калибровочным полям (какими являются, напр., поля промежуточных 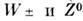 -бозонов), приобретают массу (см. Хиггса бозоны). Спонтанное нарушениедискретных С. может быть в принципе причиной появления Р- или СР- несимметричныхвакуумов в определённых частях Вселенной и объяснять наблюдаемые явлениянарушения Р- или СР-чётности.
-бозонов), приобретают массу (см. Хиггса бозоны). Спонтанное нарушениедискретных С. может быть в принципе причиной появления Р- или СР- несимметричныхвакуумов в определённых частях Вселенной и объяснять наблюдаемые явлениянарушения Р- или СР-чётности.При достаточно высоких энергиях, когда становятся возможными переходымежду различными физ. вакуумами, спонтанно нарушенная С. может восстанавливаться.
Симметрия квантовомеханических систем и вырождение. Если квантовомеханич. система обладает определённой С., то операторы сохраняющихся физ. величин, соответствующих этой С., коммутируют с гамильтонианом системы. Если нек-рыеиз этих операторов не коммутируют между собой, уровни энергии системы оказываютсявырожденными (см. Вырождение): определённому уровню энергии отвечаютнеск. различных состояний, преобразующихся друг через друга при преобразованияхС. В матем. отношении эти состояния представляют базис неприводимого представлениягруппы С. системы. Это обусловливает плодотворность применения методовтеории групп в квантовой механике.
Помимо вырождения уровней энергии, связанного с явной С. системы (напр.,относительно поворотов системы как целого), в ряде задач существует дополнит. вырождение, связанное с т. н. с к р ы т о й С. взаимодействия. Такие скрытыеС. существуют, напр., для кулоновского взаимодействия и для изотропногоосциллятора. Скрытая С. кулоновского взаимодействия, приводящая к вырождениюсостояний с разл. орбитальными моментами, обусловлена, как показал В. А. Фок (1935), явной С. кулоновского взаимодействия в 4-мерном импульсномпространстве.
Если система, обладающая к.-л. С., находится в поле сил, нарушающихэту С. (но достаточно слабых, чтобы их можно было рассматривать как малоевозмущение), происходит расщепление вырожденных уровней энергии исходнойсистемы: разл. состояния, к-рые в силу С. системы имели одинаковую энергию, под действием «несимметричного» возмущения приобретают разл. энергетич. смещения, а в случаях, когда возмущающее поле обладает нек-рой С., составляющейчасть С. исходной системы, вырождение уровней энергии снимается не полностью:часть уровней остаётся вырожденной в соответствии с С. взаимодействия,«включающего» возмущающее поле.
Наличие в системе вырожденных по энергии состояний в свою очередь указываетна существование С. взаимодействия и позволяет в принципе найти эту С.,когда она заранее неизвестна. Последнее обстоятельство играет важнейшуюроль, напр., в физике элементарных частиц.
Динамические симметрии. Оказалось плодотворным понятие т. н. динамич. С. системы, к-рое возникает, когда рассматриваются преобразования, включающие переходы между состояниями системы с разл. энергиями. Неприводимымпредставлением группы динамич. С. будет весь спектр стационарных состоянийсистемы. Понятие динамич. С. можно распространить и на случаи, когда гамильтониансистемы зависит от времени, причём в одно неприводимое представление динамич. группы С. объединяются в этом случае все состояния квантовомеханич. системы, не являющиеся стационарными (т. е. не обладающие заданной энергией).
Лит.: В и г н е р Е., Этюды о симметрии, пер. с англ., М., 1971;Гибсон У., Поллард Б., Принципы симметрии в физике элементарных частиц, пер. с англ., М., 1979; Пуанкаре А., О науке, пер. с франц., М., 1983;Эллиот Д ж., Д о б е р П., Симметрия в физике, пер. с англ., т. 1-2, М.,1983; Логунов А. А., Лекции по теории относительности и гравитации, М.,1987; Фейнман Р., Характер физических законов, пер. с англ., М., 1987.С. С. Герштейн.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.