Akademik

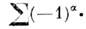
(детерминант) квадратнойматрицы А = ||a_ij|| порядка n, detA - многочлен, каждый член к-рого является произведением п элементов матрицы А,причём из каждой строки и каждого столбца матрицы в произведениевходит лишь один сомножитель, т. е. многочлен вида detA =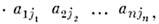где сумма берётся по всем перестановкам чисел 1, 2, ..., n; число 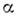равно числу инверсий в перестановке j₁, j₂,..., j_n, т. е. числу случаев, когда большее число стоитперед меньшим. O. содержит n! членов, из к-рых половина берётсясо знаком + и половина со знаком - . Число п наз. порядком О. Определительматрицы А обозначается также | А| или |det A', где А'- матрица, транспонированнаяк А; б) при чётном числе перемен местами любых двух строк (столбцов) А; в) если к элементам любой строки (столбца) прибавить соответствующиеэлементы другой строки (соответственно столбца), умноженные на одно и тоже число. 2) О. меняет знак, если в . произвести нечётное числоперемен местами любых двух строк (столбцов). 3) О. равен нулю, если:
а) все элементы к.-л. строки (столбца)равны нулю;
б) соответствующие элементы к.-л. двухстрок (столбцов) равны или пропорциональны. 4) Общий множитель всех элементовстроки (столбца) можно вынести за знак О. 5) Если каждый элемент к.-л. строки (столбца) есть сумма двух слагаемых, то О. равен сумме двух О.,причём в одном из них соответствующая строка (столбец) состоит из первыхслагаемых, а в другом - из вторых слагаемых. 6) О. можно разложить по элементамк.-л. строки (столбца). Напр., разложение О. по элементам i- й строки имеет вид: | А| = а _i1 А _i1 + а _i2A_i2+... + п -1, полученный из данного О. вычёркиванием i -йстроки и j -го столбца. 7) Из определения произведения матриц следует, что det ( АВ)= detAdetB, где А и В - квадратныематрицы одного и того же порядка. 8) detA⁺ = detA* =(detA)*, detA^-1 = (detA)^-1 при detA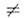0(A⁺- матрица, эрмитово сопряжённая к А, * - комплексное сопряжение).
Нек-рые спец. О.: для ф-ции f(x_l,..., х _п )гессианом наз. || д²./ дx_i дx_k||,для п ф-ций f_i (х ₁,.... х _п)(i =1, 2, ..., п )якобианом наз. О. || дf_i/ дx_j||, определителем Вронского наз. О. матрицы, в к-рой элементами первойстроки являются п функций v₁(x), v₂ (х),..., v_n(x), а их k-eпроизводные являютсяэлементами (k+ 1)-й строки(k =1, 2, ..., п -1).Определителем Грама наз. О. матрицы, элементы к-рой - скалярные произведения(u_iu_j) п векторов u₁, u₂,..., и _п в пространстве размерности п.

Лит. см. при ст. Матрица.

С. И. Азаков.