Akademik

ÉLECTRON

L’électron est une particule élémentaire stable. Il possède une charge électrique négative, une très petite masse (près de 2 000 fois plus petite que celle de l’atome le plus léger: l’hydrogène), et un moment angulaire propre appelé spin, auquel est lié un moment magnétique intrinsèque (cf. tableau). L’électron est soumis à la gravitation, ainsi qu’à la force électrofaible. En fait, c’est la partie proprement électromagnétique de cette dernière qui fait que cette particule est indispensable en chimie, en électricité, en électronique et dans la grande majorité des processus qui se trouvent à la base des techniques industrielles. Par contre, il n’est pas sensible à l’interaction nucléaire forte, ou chromodynamique, qui est notamment responsable de la cohésion des noyaux des atomes.

L’électron ne peut être correctement décrit que dans le cadre quantique, où, malgré ses propriétés variées, on le représente par une entité ponctuelle, sans dimension. C’est en ce sens qu’il reste, depuis sa découverte il y a près d’un siècle, une particule élémentaire, stable, constituant fondamental de la matière qui ne peut être brisé, et dont aucune propriété ne nécessite l’hypothèse d’une sous-structure.

L’antiparticule de l’électron est le positron, ou électron positif, qui lui est en tout point semblable, excepté pour le signe de la charge électrique. De même, l’interaction électrofaible agit différemment sur l’électron selon que son moment angulaire propre est aligné dans le sens de l’impulsion ou dans le sens opposé: on parle alors respectivement d’électron droit ou gauche.

L’électron, du fait de ses propriétés très variées (cf. tableau), s’est ainsi souvent trouvé à la base de nombreuses avancées dans la compréhension de la matière. C’est pourquoi une approche historique de l’établissement de ces caractéristiques est importante pour comprendre la nature profonde du concept de l’électron.

Découverte de l’électron

L’électron a été la première particule élémentaire mise en évidence et son acceptation par la communauté scientifique a duré près d’un siècle, depuis la caractérisation des lois de l’électrolyse par Faraday en 1833 jusqu’à la reconnaissance de l’électron vers 1920. Mais la détermination de la masse et de la charge du corpuscule par Joseph John Thomson en 1897 marque la date de la découverte de l’électron. En étudiant la décomposition de solutions par le courant électrique, Faraday avait établi que, pour une même quantité d’électricité, le poids de matière déposée par les ions varie dans des rapports semblables à ceux qui interviennent dans les réactions chimiques et, plus précisément, que tous les atomes-grammes d’ions monovalents portent la même charge, appelée maintenant le faraday.

Au cours du XIX^e siècle, la théorie atomique s’imposa progressivement. Elle suppose que chaque atome-gramme contient le même nombre d’atomes élémentaires, le nombre d’Avogadro N. Il s’ensuit que chaque ion porte une charge unique, identique quel que soit le composé monovalent particulier. Pour les tenants de cette théorie, cette charge élémentaire put être calculée vers 1870 lorsque Johann Loschmidt et d’autres fournirent une estimation du nombre N d’atomes par atome-gramme.

L’Irlandais George J. Stoney, lui-même auteur d’une évaluation de N, calcula une valeur de cette charge élémentaire en 1874, et il la baptisa «électron» en 1891, reprenant ainsi le nom grec de l’ambre gris dont les propriétés avaient été à l’origine de la découverte de l’électricité.

L’électron n’était alors qu’une charge élémentaire transportée par les ions. C’est au cours de l’étude des propriétés électriques des gaz sous très faible pression que la particule allait apparaître: lorsqu’on applique une forte tension entre deux électrodes dans un tube contenant un gaz suffisamment raréfié, on obtient des rayons émis par l’électrode négative, ou cathode, qui se propagent en ligne droite, et qu’on peut observer grâce aux vives luminescences produites sur certaines parties de la paroi de verre du tube. En 1895, Jean Perrin réussit à démontrer que ces rayons transportent des charges négatives. En 1897, J. J. Thomson, en appliquant des champs électriques et magnétiques, put mesurer le rapport e /m de la charge à la masse des composants de ces rayons, et le trouva près de 2 000 fois plus grand que pour les ions hydrogène. Compte tenu de la constance de cette valeur pour toutes sortes de matériaux et de gaz, il fut amené à postuler l’existence de «corpuscules cathodiques», beaucoup plus légers que les atomes, dont ils devaient être un composant universel: il s’agissait d’une nouvelle forme de matière, que nous appelons maintenant un électron.

Le même concept devait apparaître simultanément dans une autre branche de la physique: l’étude des raies lumineuses émises par les atomes. Après les tentatives infructueuses de plusieurs chercheurs, le Néerlandais Pieter Zeeman, en 1896, réussit à observer un effet du champ magnétique sur les raies jaunes du sodium: elles étaient élargies, et de manière différente selon que la direction d’observation était parallèle ou perpendiculaire à celle du champ magnétique. Aussitôt, le physicien néerlandais Hendrik Antoon Lorentz réussit à expliquer le phénomène en supposant l’existence dans l’atome d’un ion oscillant à la fréquence d’émission du rayonnement. Avec ce modèle, Zeeman trouva que le rapport e /m nécessaire pour reproduire les expériences était de plus de 1 000 fois celui de l’ion hydrogène. Ce n’est qu’après l’interprétation corpusculaire de Thomson que l’«ion» oscillant put être assimilé à la particule des rayons cathodiques. Par la suite, des études plus précises de Zeeman sur la polarisation de la lumière des raies dédoublées montra que la particule source du rayonnement dans l’atome avait une charge négative.

De nombreuses données vinrent ensuite confirmer ces résultats. Dès 1899, Thomson avait établi que les particules émises par les rayons ultraviolets dans l’effet photoélectrique ont le même rapport e /m que celles des rayons cathodiques. Il avait surtout obtenu une première mesure directe de la charge électrique individuelle, au moyen des gouttes de condensation dans une vapeur sursaturée, selon un procédé inventé par Charles Thomson Rees Wilson. Cela fut confirmé plus tard par les mesures très précises de la charge de l’électron réalisées par Robert Andrews Millikan en 1909: des gouttelettes d’huile chargées électriquement tombent par gravité entre les plaques d’un condensateur, et l’on équilibre le poids par l’attraction électrique. Toutes les charges sont multiples d’une valeur commune unique, e .

Auparavant, une confirmation indirecte, qui montre bien les liens entre les divers domaines de la physique, avait été fournie par Max Planck en 1901: à partir de sa loi sur le rayonnement des corps chauds, il put établir tout d’abord une valeur précise de la constante de Boltzmann k , puis, à partir de la constante des gaz R = Nk , celle du nombre d’Avogadro N, et enfin, avec le faraday F = Ne , celle de la charge élémentaire qu’il trouva en bon accord avec les résultats de Thomson. Durant cette même époque, Pierre et Marie Curie démontrèrent que les rayons 廓 de la radioactivité (qui avait été découverte par Henri Becquerel en 1896) étaient eux aussi formés de corpuscules chargés négativement pour lesquels Becquerel trouva une valeur de e /m similaire à celle des rayons cathodiques.

L’électron classique

La mesure du rapport e /m du «corpuscule cathodique» ou de l’«ion oscillant», effectuée respectivement par J. J. Thomson et par P. Zeeman, est fondée sur l’une des lois de H. A. Lorentz mise au point lors de l’élaboration d’une interprétation de l’électromagnétisme de Maxwell (cf. ÉLECTRICITÉ - Histoire de l’électricité) au moyen de courants de particules chargées:

où づ, appelée maintenant force de Lorentz, représente la force exercée par des champs électriques つ et magnétiques ち sur une particule de charge e et de vitessev.

La théorie de Lorentz était fondée sur l’électromagnétisme, allié à la mécanique newtonienne ^{[cf. LORENTZ (H. A.)]}. Dans l’expérience de J. J. Thomson , une première mesure consistait à étudier le déplacement des rayons cathodiques dans des champs électriques et magnétiques perpendiculaires entre eux et aux rayons. Pour une certaine valeur du rapport des champs, le déplacement des rayons est nul car les deux composantes de la force de Lorentz se compensent lorsque v = E/B, ce qui fournit une mesure de la vitesse. Celle-ci est trouvée notablement plus faible que celle de la lumière. Dans le champ électrique seul, le déplacement est semblable à une chute libre avec pour accélération (e E/m ); donc, pour une longueur l dans le champ, le déplacement sera:

et l’étude de ce déplacement en fonction du champ électrique, une fois v connu, permet la mesure du rapport de la charge à la masse.

Dans cette expérience sont déjà en germe non seulement des objets aussi usuels qu’un tube de téléviseur, qui n’est autre qu’un tube à rayons cathodiques agrandi, mais aussi les accélérateurs de particules, les spectromètres de masse utilisés pour l’analyse des gaz, ou bien les oscilloscopes des électroniciens.

Dans l’expérience de Zeeman , le mouvement harmonique de la charge dans l’atome est perturbé par la force de Lorentz et, si celle-ci est suffisamment petite par rapport à la force de rappel de l’oscillateur, son effet dans le plan perpendiculaire au champ magnétique est de déplacer la fréquence de:

d’où la mesure de e /m à partir de l’élargissement des raies (cf. effet ZEEMAN).

Le rayonnement des atomes excités, considérés comme des oscillateurs harmoniques, utilise une propriété subtile de l’électromagnétisme: toute charge accélérée rayonne de la lumière. L’énergie rayonnée freine l’oscillation, qui est ainsi amortie, et doit s’arrêter. Le champ électrique rayonné à l’instant t et à une distance r par une charge q soumise à une accélération a est:

où a est l’accélération «retardée» que la particule avait à l’instant t 漣 (r /c ), c étant la vitesse de la lumière et 﨎⁰ la permittivité du vide. Pour un oscillateur harmonique, de pulsation 諸 et d’élongation x , a = 諸²x , et a = a si le mouvement a une vitesse faible en comparaison de celle de la lumière: la fréquence émise est alors celle du mouvement. La puissance rayonnée est:

où e ² = q ²/(4 神﨎⁰) et où x ⁰ est l’élongation maximale, alors que l’énergie de l’oscillateur est W = (m 諸²x ²⁰)/2: le décrément par pulsation est 1/Q = (4 神e ²)/(3mc ²), si bien qu’une raie visible de 600 nm de longueur d’onde perd les deux tiers de son intensité en 10^-8 s. La propriété de rayonnement des électrons a été longtemps une difficulté insurmontable pour les modèles classiques d’un atome planétaire formé d’un noyau positif lourd entouré d’électrons en mouvement harmonique autour de lui: la perte d’énergie par rayonnement garantissait l’effondrement des électrons sur le noyau! Il a fallu l’audace de Niels Bohr pour supposer une disparition de cet effet dans les atomes, et poser ainsi les jalons du modèle atomique quantique où une telle suppression du rayonnement a effectivement lieu.

L’accélération centripète subie par un électron tournant sur une trajectoire circulaire dans un accélérateur de particules, appelé à l’origine synchrotron à électrons, produit un rayonnement similaire à celui d’un atome. Cependant, du fait de l’accélération, la vitesse devient progressivement proche de celle de la lumière, et le rayonnement se produit aussi à des fréquences double, puis triple, etc., de celle du mouvement ou fréquence fondamentale. La structure en harmoniques du rayonnement s’efface dans une émission avec des fréquences variant de façon continue: c’est ce qu’on appelle le rayonnement synchrotron (cf. rayonnement SYNCHROTRON). Un électron en mouvement circulaire a une énergie beaucoup plus élevée que celle de sa masse, donc avec 塚 = E/mc ² grand; il est alors une sorte de phare émettant dans un cône d’ouverture 1/ 塚 autour de sa vitesse. Ce rayonnement se traduit par une perte d’énergie dans les accélérateurs à électrons que l’on compense par un apport sous forme d’un champ électrique accélérateur. La perte d’énergie par tour de rayon R est:

où 廓 = v/c . Elle est proportionnelle à la puissance quatrième du rapport 塚 = E/mc ², si bien que seuls les électrons, particules chargées les plus légères, peuvent rayonner beaucoup.

Cette perte d’énergie a conduit à construire des accélérateurs à électrons de très grand rayon, pour compenser la croissance du rayonnement avec l’énergie: le L.E.P. (Large Electron Positron Collider), grand collisionneur électron positron, en service depuis le mois de juillet 1989 au Laboratoire européen de physique des particules du C.E.R.N. à Genève, est le plus grand accélérateur du monde, avec un rayon de plus de 4 km et 27 km de circonférence. Il atteint 100 GeV, soit 塚 力 200 000 (cf. Les anneaux de stockage d’électrons, in rayonnement SYNCHROTRON).

Le rayonnement synchrotron a été découvert dans la nature. L’observation en lumière polarisée de la nébuleuse du Crabe, restes de la supernova observée par les Chinois en 1054, montre l’existence de filaments lumineux émettant selon un spectre continu: le rayonnement est vraisemblablement produit par des trajectoires d’électrons tournant à grande vitesse autour de longues lignes de champ magnétique.

Une difficulté de la théorie classique de l’électron concerne la description de la particule elle-même: son énergie électrostatique au repos est e ²/r , où r est une distance caractéristique finie, sinon l’énergie propre serait infinie. En supposant que cette dernière fournit la masse de l’électron, on en déduit r , appelé «rayon classique de l’électron»: r ^e = e ²/mc ², et on doit penser l’électron comme une petite sphère... mais quelle force empêche la répulsion électrostatique de la faire exploser? De plus, avec la théorie de la relativité restreinte, ou, ce qui revient au même, si l’on suit les lois de transformation de l’électromagnétisme, un tel électron en mouvement s’aplatit et l’équilibre, un instant restauré par ces forces de liaison, est de nouveau rompu. Si bien que, malgré de nombreuses tentatives de solution, le problème resta entier: un électron est une particule ponctuelle pour toute interaction extérieure, mais lui-même n’est pas décrit par le concept de Lorentz. On peut anticiper ici en disant que la théorie quantique ne fait pas beaucoup mieux, mais les difficultés correspondantes ont conduit à la fructueuse méthode de la renormalisation (cf. théorie des CHAMPS).

L’électron quantique

La théorie quantique de l’électron a commencé par l’hypothèse de Louis de Broglie en 1923, qui suggère que l’association onde-corpuscule observée pour le photon est universelle: il associe à l’électron en mouvement une longueur d’onde = h /p , où p est l’impulsion et h la constante de Planck et il prédit qu’un électron doit donc être capable de diffraction.

En 1927, les physiciens américains Clinton Davisson et Lester Germer détectent la diffraction des électrons par un cristal de nickel. Cette découverte fut quelque peu accidentelle: à la suite d’une fausse manœuvre, ils avaient pollué un échantillon de nickel sur lequel ils étudiaient sous vide la diffusion des électrons. Ils décidèrent donc de le chauffer longuement en atmosphère d’hydrogène, pour décomposer les oxydes formés à la surface. Quand ils reprirent leur expérience, les électrons diffusés étaient rassemblés en taches, en tout point semblables aux taches de von Laue qu’on observe dans la diffusion des rayons X par un cristal: pendant l’échauffement, le nickel polycristallin s’était transformé à leur insu en monocristal. La connaissance de la maille du réseau cristallin leur permit de calculer la longueur d’onde des électrons, et la valeur trouvée était en bon accord avec la relation de Louis de Broglie (cf. rayons X).

C’est dans le cadre de la mécanique quantique développée à cette époque que cette découverte prendra tout son sens (cf. mécanique QUANTIQUE). En tout cas, un des effets utiles de cette propriété est de permettre de construire, avec des électrons, des systèmes optiques de très grande sensibilité, car la limite de diffraction peut être repoussée en augmentant l’énergie des électrons.

Le pouvoir de résolution d’un microscope est limité par la diffraction à la valeur 1,22/sin , où est la longueur d’onde et , l’ouverture angulaire de l’objectif. Dans un microscope électronique, les champs magnétiques et électriques permettent de construire des lentilles suffisamment précises, en même temps que l’accélération des électrons diminue la longueur d’onde (cf. MICROSCOPES - Microscopes électroniques). La limite est atteinte quand l’énergie dans le faisceau devient assez importante pour risquer de détruire l’échantillon à étudier: les microscopes électroniques les plus puissants ne sont utilisables à leur limite de résolution qu’avec des échantillons capables de résister à l’énergie reçue, mais ils peuvent rendre visibles les molécules.

Un avatar particulier du microscope électronique est l’accélérateur de particules. De fait, de telles machines ont servi à mesurer la taille des noyaux des atomes, puis celle du proton lui-même. La sous-structure formée par les quarks et les gluons dans les protons et les neutrons a été découverte en 1968 à Stanford (États-Unis) avec un accélérateur de plus de 3 km de longueur.

Une prochaine étape dans cette voie sera réalisée par les collisions en vol entre des faisceaux d’électrons de 20 GeV et de protons de 800 GeV dans l’anneau H.E.R.A. (Hadron Electron Ring Accelerator) à Hambourg: l’énergie disponible dans le centre de masse de la collision est de 250 GeV, permettant en principe d’atteindre des objets de 10^-18 m: un domaine tout à fait nouveau est ainsi exploré depuis 1991.

Le spin de l’électron

Avant que l’expérience de Davisson et Germer ne vînt prouver la réalité de la diffraction de l’électron, une autre propriété allait lui être attribuée: un moment angulaire intrinsèque appelé spin, qui signifie ici tourner sur soi-même ^{[cf. SPIN]}. La découverte du spin trouve sa source une fois encore dans l’étude des spectres d’émission des atomes, et même dans l’étude de l’effet Zeeman. Dès 1898, grâce à l’amélioration de la précision des mesures, Cornu avait découvert que la raie jaune D1 du sodium est décomposée en quatre raies par un champ magnétique, alors que la théorie classique n’en prédit au plus que trois. On s’était aperçu ensuite que la plupart des raies atomiques produisent des nombres variés de raies, ce qu’on a appelé l’effet Zeeman «anormal» par opposition à l’effet Zeeman «normal» de la théorie de Lorentz.

Vers 1920, les calculs de niveaux atomiques permis par le modèle d’atome de Bohr donnaient accès à une nouvelle compréhension des atomes hydrogénoïdes, au moyen des trois nombres quantiques principal, orbital et magnétique. En 1921, le physicien allemand Alfred Landé avait pu expliquer l’effet Zeeman «anormal» en introduisant des nombres quantiques demi-entiers. Le déplacement en énergie observé n’était plus exactement proportionnel au produit de l’induction du champ magnétique B par le magnéton 猪^B multiplié par le nombre magnétique m : Landé devait ajouter un facteur g voisin de 1:

En 1924, Wolfgang Pauli montrait que l’idée de Landé conduisait à attribuer à l’électron un nombre quantique supplémentaire qui ne pouvait prendre que deux valeurs. Cela permettait d’expliquer les nombres d’électrons observés dans chaque couche atomique, en posant que chacun d’entre eux doit avoir un ensemble de nombres quantiques, y compris le quatrième, différent. Chaque jeu de nombres quantiques définit un état qui ne peut être occupé que par un seul électron: c’est ce que l’on appelle le principe d’exclusion de Pauli ^{[cf. PAULI (W.)]}.

Durant l’été de 1925, deux jeunes physiciens néerlandais, George Uhlenbeck et Samuel Goudsmit, reliaient ce quatrième nombre à un degré de liberté supplémentaire de l’électron: classiquement, ce dernier peut tourner sur lui-même avec un moment angulaire propre d’un ½ h et avec un facteur de Landé égal à 2 (cf. Spectroscopie de l’hydrogène et de l’hélium , in SPECTROSCOPIE - Spectroscopie atomique). Ils trouvèrent même un modèle d’électron en couche sphérique où le moment magnétique résultant avait ce facteur 2, tout en étant conscients des limites d’une telle interprétation classique. Il faut, en fait, l’équation de Dirac pour comprendre l’origine quantique du facteur de Landé de l’électron.

Le principe d’exclusion de Pauli a pour conséquence que les électrons obéissent à des lois statistiques différentes de celles des photons: ils suivent la statistique de Fermi-Dirac, qui, par exemple, est déterminante pour comprendre correctement les propriétés des métaux. La liaison entre le spin et la statistique est démontrée dans la théorie quantique des champs: tous les objets de spin demi-entier, décrits par des opérateurs qui anticommutent, suivent la statistique de Fermi-Dirac, alors que les spins entiers, dont les opérateurs commutent, suivent celle de Bose-Einstein, selon laquelle les particules tendent au contraire à se mettre toutes dans le même état quantique (cf. mécanique STATISTIQUE et théorie des CHAMPS).

Le principe d’exclusion a une importance fondamentale: c’est à cause de lui que les atomes ont une extension finie et qu’ils ne s’interpénètrent pas. Il est indispensable pour comprendre comment la matière qui nous entoure tient en équilibre malgré la très petite fraction de l’espace réellement occupée par les composants des atomes.

L’équation de Dirac et le positron

Avec le développement de la mécanique quantique, la description de l’électron et de son spin a posé un problème nouveau. Il a d’abord été partiellement résolu par Pauli au moyen d’une fonction d’onde à deux composantes, ou spineur, sur laquelle agissait un ensemble de matrices deux par deux représentant l’opérateur de spin. Le facteur de Landé devait être introduit explicitement, de même que les corrections relativistes. Mais l’opérateur ainsi construit permettait d’écrire une équation avec laquelle, pour la première fois, un calcul correct de l’atome d’hydrogène était possible. Le physicien anglais Paul Dirac ^{[cf. DIRAC (P.)]} avait abouti indépendamment à des conclusions similaires à celles de Pauli, mais avait voulu une équation où l’invariance relativiste fût manifeste dès le départ. En 1927, il en proposait une, qui reposait sur des spineurs à quatre composantes 祥, sur lesquels agissaient des opérateurs matriciels quatre par quatre 塚 size=1^猪, formés chacun avec les matrices de Pauli. Ces derniers sont liés ensemble pour former un quadrivecteur de l’espace-temps, ce qui est indiqué par l’indice 猪 qui court sur la dimension temps et sur les trois dimensions d’espace. Dans sa formulation moderne, l’équation de Dirac s’écrit pour un électron en interaction avec un potentiel électromagnétique A size=1^猪:

Cette équation n’inclut que des dérivées au premier ordre, et ses solutions s’interprètent de la même manière que celles de l’équation de Schrödinger. Mais l’interaction avec le champ électromagnétique comprend tous les résultats relativistes. La surprise fut qu’elle fournit aussi naturellement le mystérieux facteur de Landé g = 2. Enfin, son approximation à basse énergie reproduit les résultats non relativistes: une étape immense était franchie.

Mais cette équation engendra aussi de sévères paradoxes: les solutions contenaient deux fois trop d’états, à cause des quatre composantes de la fonction d’onde, là où deux seulement étaient nécessaires. Dirac lui-même avait diagnostiqué la cause: cela provient de ce que l’équation relativiste entre l’énergie, l’impulsion et la masse E² = p ²c ² + m ²c ⁴ a deux solutions E = 梁 連p ²c ² + m ²c ⁴ ..., et que faire des solutions à énergie négative? Après divers tâtonnements, il fut convaincu qu’elles représentaient des électrons de charge positive. La nouvelle particule correspondante, le positron, fut découverte en 1932 par Carl Anderson dans des clichés de rayons cosmiques obtenus dans une chambre à brouillard de Wilson.

Le positron est un antiélectron, au sens que sa rencontre avec un électron se traduit par une transformation commune en énergie. Ce processus est appelé annihilation. Selon l’énergie de l’électron et du positron, l’annihilation peut produire toutes sortes de particules: les collisions électron-positron constituent maintenant le moyen principal d’étude des interactions élémentaires. À basse énergie, le seul canal d’annihilation possible est l’apparition de deux photons:

À l’opposé, un photon passant dans le champ électrique d’un noyau atomique ou d’un électron peut se transformer en matière par création d’une paire électron-positron, si l’énergie disponible dans le centre de masse de la collision dépasse deux fois l’énergie de masse de l’électron.

Il s’agit, en fait, d’une propriété générale de la matière: à toute particule correspond une antiparticule avec laquelle elle peut s’annihiler. Notre compréhension actuelle des débuts de l’Univers repose sur la création simultanée de matière et d’antimatière à partir de l’énergie initiale, suivie plus tard de l’annihilation de la presque totalité des particules, sauf pour une fraction résiduelle due à une asymétrie des interactions. C’est cette fraction qui constitue la matière de notre Univers ^{[cf. ANTIMATIÈRE]}.

Le positron a la même masse que l’électron, la même charge mais de signe opposé, le même spin. C’est une particule image de l’électron dans une symétrie de charge, que la plupart des interactions des particules respectent, sauf la partie nucléaire faible de l’interaction électrofaible.

Le positron est actuellement utilisé en médecine. Il existe des composés comprenant un noyau radioactif 廓⁺, capable de l’émettre. Un tel composé peut se fixer sur un organisme, et, lorsqu’il émet un positron, celui-ci s’annihile très près du point d’émission en envoyant deux photons dans des directions opposées. La détection de ces derniers permet de reconstruire le point d’émission avec précision, et ainsi d’étudier l’organisme comme souhaité: c’est ce qu’on appelle la tomographie par positrons.

L’électrodynamique quantique

L’apparition du positron a complètement changé la compréhension de la théorie de Dirac. Dans la conception quantique, le vide a des fluctuations en énergie. Quand celles-ci sont assez élevées, une paire e ⁺e ^- peut se former de manière éphémère, la durée étant donnée par le principe d’incertitude de Heisenberg t 年 領 /2mc ², soit environ 10^-21 s. Ces états sont appelés virtuels. Au voisinage d’un électron, le champ de celui-ci a tendance à séparer ces paires virtuelles, créant un phénomène de polarisation électrique du vide. Il s’ensuit que la charge de l’électron effectivement sentie par une autre particule sera diminuée légèrement. Un tel effet peut être calculé par la théorie de Dirac. La réponse est qu’il faut soustraire une charge infinie!

En fait, il faut comprendre que la charge de l’électron telle que nous la mesurons est déjà réduite par l’effet d’écran dû à la polarisation du vide; mais, alors, la charge de l’électron nu, si une telle chose existe, serait infinie.

Malgré ses énormes succès, le concept de Dirac butait donc sur des difficultés. Sa transposition dans le langage de la théorie des champs permit de réaliser des calculs biens vérifiés par l’expérience, en utilisant le permier terme d’un développement en série avec, comme paramètre, la constante de structure fine:

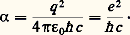
La mesure de l’effet Josephson fournit 見 = 1/137,035 989 5(61). Mais, bien que le paramètre effectif de développement soit 見/ 神 (1/400 environ), le calcul des termes d’ordre plus élevé se heurtait à des infinités similaires à celle qui est mentionnée plus haut.

Au cours des vingt années suivantes, on arriva d’abord à une compréhension correcte de ces infinités, au moyen de la théorie de la renormalisation, et, en même temps, à une formulation intuitive de l’électrodynamique quantique au moyen des diagrammes d’espace-temps inventés par Richard Feynman ^{[cf. FEYNMAN (R. P.)]}, alors que Julian Schwinger et Sin-Itiro Tomonaga arrivaient indépendamment à des conceptions équivalentes: l’électrodynamique quantique (E.D.Q.) était née (cf. électrodynamique QUANTIQUE).

Avec une série de prescriptions univoques, et pour seuls paramètres la masse de l’électron et sa charge (ou 見), elle permet de calculer, à une précision aussi petite que l’on veut, toute quantité mettant en jeu des électrons et la force électromagnétique, tout en reproduisant les résultats des théories précédentes, qui apparaissent comme des approximations dont le domaine de validité est clairement établi.

Un exemple célèbre est le calcul du moment magnétique de l’électron. Comme l’équation de Dirac, l’E.D.Q. à l’ordre le plus bas fournit le facteur g égal à 2; mais des corrections sont apportées par les termes d’ordre supérieur. La quantité mesurée expérimentalement est a = (g 漣 2)/2, c’est-à-dire le complément à 1 du facteur de proportionnalité entre le moment magnétique de l’électron et un magnéton de Bohr.

Les mesures sont extrêmement précises, car elles atteignent directement a comme différence entre la fréquence dite cyclotron de rotation d’un électron sur une orbite, et la précession du moment magnétique autour de l’électron. Les meilleures mesures sont faites en piégeant un électron dans des champs magnétiques et électriques croisés sur une orbite toroïdale, puis en excitant les transitions entre les deux états d’énergie, dus à l’orientation du moment magnétique, au moyen d’un champ hyperfréquence. La valeur trouvée par Hans Dehmelt et son équipe en 1987 est:

Dans le calcul au premier ordre, on a g = 2 et donc a = 0. À l’ordre suivant, on trouve a = 見/2 神 (Schwinger, 1948). C’est le terme principal de la correction, et ce fut un des premiers grands succès de l’E.D.Q.

Avec la précision des mesures, il a fallu que l’on calcule cette quantité aux ordres suivants du développement en série, ce qui n’est pas une mince affaire, car le nombre de termes à calculer augmente très vite: il y en a 7 à l’ordre 見², 72 en 見³, et 891 en 見⁴... Le meilleur résultat théorique est actuellement:

moins précis que la mesure; mais l’incertitude provient de celle de la valeur de 見 donnée plus haut. Il y a, en tout cas, un accord excellent:

et bien peu de conceptions ont été testées à ce niveau de précision. D’autres quantités ont été mesurées et calculées avec un accord similaire, notamment les transitions de l’atome d’hydrogène: l’électrodynamique quantique est une excellente théorie.

Force électrofaible et théorie de jauge

On a noté plus haut que, très tôt après la découverte de la radioactivité, les rayons 廓 avaient été identifiés comme composés d’électrons. L’étude de cette forme de radioactivité devait d’abord conduire Pauli à prédire l’existence d’une particule émise avec chaque électron 廓: le neutrino-électron 益^e , particule sans masse et sans charge, mais avec un spin demi-entier.

Puis Enrico Fermi, en 1933, postula une nouvelle sorte d’interaction pour l’électron: l’interaction faible. Certains noyaux et le neutron n lui-même se décomposent selon:

Il s’agit d’une forme nouvelle de création de particules, car apparaissent, en plus du proton p , un électron e ^- et une antiparticule, l’antineutrino 益^e associé à l’électron. Cette règle de création simultanée est celle de la conservation du nombre électronique.

La théorie de Fermi prédit l’existence d’une deuxième réaction:

Sa mise en évidence, en 1956, par Frederick Reines et Clyde L. Cowan, en utilisant un réacteur nucléaire, prouva l’existence du neutrino.

Par la suite, un grand nombre de décompositions de particules ont été observées, avec des régularités qui ont conduit à la notion d’universalité de l’interaction de Fermi: elle est identique pour les électrons et pour les muons 猪 et les tauons 精, qui apparaissent comme des électrons lourds: m size=1^猪 = 105,66 MeV/c ², m size=1^精 = 1 784,1 MeV/c ², auxquels sont associés leurs propres neutrinos. On a ainsi trois familles semblables.

En 1957, des anomalies dans les observations de certaines décroissances conduisirent Tsung-Dao Lee et Chen-Ning Yang à étudier la possibilité d’une violation de la symétrie de parité. Cette symétrie était utilisée depuis Wigner pour la classification des transitions atomiques. Lee et Yang remarquèrent qu’aucune expérience d’interaction faible ne l’avait testée, et proposèrent des mesures dans ce but (cf. SYMÉTRIE [physique]). Il s’agit, en principe, de vérifier la propriété d’identité des interactions dans deux montages expérimentaux images l’un de l’autre dans un miroir. En fait, on mesure les directions des électrons par rapport à une direction privilégiée dans une décroissance faible, et l’on cherche une asymétrie dans les angles d’émission.

Peu après, la physicienne Chien-Shiung Wu et ses collaborateurs établissaient que la parité était violée dans la décroissance 廓 du cobalt-60 magnétisé, et cette observation fut confirmée très vite dans d’autres expériences. Cela conduisit à une théorie dans laquelle le neutrino n’a qu’une seule orientation de spin, toujours dans la direction opposée à son mouvement: il est gauche, et la conservation de cette hélicité se traduit par une violation maximale de la parité dans l’interaction nucléaire faible. Par suite de la conservation du nombre électronique, il s’ensuit que, à haute énergie, seuls les électrons gauches sont soumis à cette force.

L’interaction de Fermi ne peut être renormalisée; des calculs au premier ordre ont donc été les seuls possibles. Des tentatives pour améliorer cette situation en introduisant une particule échangée dans l’interaction faible se heurtaient au fait que ce «boson intermédiaire» devait être lourd et chargé électriquement, si bien que la théorie n’était pas non plus renormalisable (cf. Renormalisation , in théorie des CHAMPS).

Un fait nouveau apparut en 1967 quand Sheldon Lee Glashow, Abdus Salam et Steven Weinberg trouvèrent un modèle avec, en plus, un boson neutre, sorte de photon lourd violant la parité, mais avec lequel le photon électromagnétique a des liens étroits. Ce modèle était en fait une unification de l’électrodynamique quantique avec l’interaction faible nucléaire; il prédisait un phénomène qu’on n’avait encore jamais observé: l’interaction faible neutre via le boson appelé Z⁰, gouvernée par un paramètre nommé angle de Weinberg ^W. Les auteurs pensaient que ce modèle pouvait être en fait une théorie de champ renormalisée, et ce fut démontré par Gerhard ’t Hooft en 1971. C’était un pas considérable, car c’était la première fois depuis l’E.D.Q. qu’une théorie renormalisable était appliquée à une interaction physique.

Les interactions neutres faibles prédites furent observées par André Lagarrigue et ses collaborateurs en 1973, en étudiant les interactions des neutrinos ^{[cf. NEUTRINOS]}. La mesure résultante de l’angle de Weinberg permettait de prédire avec précision les masses des bosons intermédiaires W⁺, W^- et Z⁰, qui furent observés directement en 1983 par Carlo Rubbia et ses collaborateurs au moyen de collisions proton-antiproton ^{[cf. PROTON]}. L’électron a donc des charges faibles, qu’on appelle isospin et hypercharge. Ici encore, l’électron est représenté par un champ ponctuel, sans dimension géométrique et sans sous-structure.

On retrouve, pour la théorie électrofaible, les qualités de l’E.D.Q.: toute grandeur mesurable peut être calculée avec une précision arbitraire, mais au prix de difficultés encore plus grandes; c’est aux expériences de fournir les résultats précis pour la tester. Comme l’E.D.Q., la théorie électrofaible utilise une découverte théorique d’une grande beauté: le principe d’invariance de jauge. En un mot, cela consiste à imposer aux champs libres une propriété d’invariance par rapport à un groupe interne de transformations, mais avec des paramètres de transformation qui sont arbitraires en chaque point de l’espace-temps. Les contraintes imposées par cette demande ne permettent qu’une seule solution: l’interaction observée.

Les tests de cette théorie sont en cours depuis la découverte des courants neutres en 1973 (cf. Les théories de jauge et Les courants neutres , in PARTICULES ÉLÉMENTAIRES). Les expériences concernent aussi bien les énergies extrêmement élevées nécessaires pour créer les bosons W et Z et les étudier au L.E.P., que les transitions atomiques à quelques dixièmes d’électronvolt. Il est remarquable que, dans toute cette gamme, les mesures de sin^{2 W} sont en excellent accord, à la précision des mesures près, qui ne cesse de s’améliorer:

L’observation de minuscules effets de violation de la parité dans les transitions atomiques ouvre aussi une nouvelle perspective pour comprendre l’asymétrie droite-gauche des molécules biologiques, découverte par Pasteur en 1857; mais il ne s’agit pour l’instant que d’une voie de recherche.

Une unification de la théorie électrofaible avec la force nucléaire forte et même avec la gravitation sera peut-être réalisée. Peut-être la mystérieuse existence de trois familles sera-t-elle comprise? L’électron pourrait alors être ramené à l’état de particule démocratiquement mélangée aux autres.

Son importance pratique restera cependant unique, car il apparaît dans un très grand nombre de domaines utiles, dont quelques-uns ont été mentionnés. Il en apparaîtra certainement de nouveaux, telle est la diversité des propriétés de l’électron et son ubiquité dans tous les matériaux.

• 1894; « matière électrique » 1808; en angl., 1891 (Stoney); du rad. de electric, et p.-ê. -on de ion, d'apr. le gr. êlektron « ambre »

1 ♦ Particule élémentaire de masse très faible (⇒ lepton). Électron positif. ⇒ positon.

2 ♦ Cette particule chargée négativement, élément constitutif de l'atome, de masse égale à 1/1836 de la masse du proton. Le nombre d'électrons circulant autour du noyau de l'atome est égal au nombre de charges positives du noyau (protons). Interactions faibles entre les électrons et le noyau. Électron célibataire, électron libre, isolé, non apparié (⇒ covalence) . L'aptitude des électrons de l'atome à s'échanger explique les propriétés chimiques de celui-ci (⇒ valence) . — Techn. Usinage par faisceau d'électrons. Canon à électrons. — Loc. fig. Électron libre : personne qui agit de manière indépendante (par rapport à un ensemble, une institution).

n. m. Particule constitutive de la partie externe de l'atome, qui porte une charge électrique négative de 1,602.10 -19 coulomb et a une masse de 0,911.10 -30 kg. (V. encycl. particule et électronique.)

⇒ÉLECTRON, subst. masc.

Particule portant une charge électrique élémentaire négative. Spin d'un électron, faisceau d'électrons. Synon. négaton (cf. conduction ex. 2). Dans les conducteurs, évoluent des électrons libres dont le déplacement dirigé engendre les courants (Hist. gén. sc., t. 3, vol. 1, 1961, p. 186). Émission d'électrons par les métaux chauffés (effet thermo-ionique) (Hist. gén. sc., t. 3, vol. 2, 1964, p. 260).

— P. ext. Particule portant une charge électrique élémentaire. Électron positif (positon), électron négatif (négaton) :

• Un électron de très grande énergie, freiné brutalement dans le champ électrique intense d'un noyau, rayonne une partie de son énergie en émettant un photon. Le photon, au voisinage d'un noyau, peut se matérialiser en une paire d'un électron positif et d'un électron négatif.

Hist. gén. sc., t. 3, vol. 2, 1964 p. 373.

Rem. On rencontre ds la docum. le subst. masc. électron-volt. Unité d'énergie utilisée en physique atomique, égale à l'énergie acquise par un électron en mouvement dans le vide sous une différence de potentiel de un volt (abrév. eV). Un synchrotron à protons de trois milliards d'électrons-volts (GOLDSCHMIDT, Avent. atom., 1962, p. 119). On rencontre également ds la docum. le plur. électron-volts. 10 électron-volts (Hist. gén. sc., t. 3, vol. 2, 1964, p. 321).

Prononc. et Orth. :[]. Ds Ac. 1932. Étymol. et Hist. 1902 (H. POINCARÉ, Science et Hypoth., p. 194 ds BONN.). Empr. à l'angl. electron (electr[ic] + on de anion, cation), nom donné à l'atome électrique par le physicien anglais G.-J. Stoney (cf. 1891, Trans. Roy. Dublin Soc. ds NED Suppl.² : These charges [of negative electricity], which it will be convenient to call electrons). Fréq. abs. littér. :68. Bbg. BONN. 1920, p. 180. — DUB. Dér. 1962, p. 66.