- СТАТИСТИЧЕСКАЯ ФИЗИКА
-
раздел физики, посвящённый изучению св-в макроскопич. тел, т. е. систем, состоящих из очень большого числа одинаковых ч-ц (молекул, атомов, эл-нов и т. д.), исходя из св-в этих ч-ц и вз-ствий между ними.Изучением макроскопич. тел занимаются и др. разделы физики — термодинамика, механика сплошных сред, электродинамика сплошных сред, гидродинамика. Однако при решении конкретных задач методами этих дисциплин в соответствующие ур-ния всегда входят неизвестные параметры или ф-ции, характеризующие данное тело. Так, для решения задач гидродинамики необходимо знать уравнение состояния жидкости или газа, теплоёмкость жидкости, её коэфф. вязкости и т. п. Все эти зависимости и параметры можно, разумеется, определять экспериментально, поэтому методы, о к-рых идёт речь, наз. феноменологическими. Статистическая же физика позволяет, по крайней мере в принципе, а часто и фактически, вычислить все эти величины, если известны силы вз-ствия между атомами и молекулами. Т. о., С. ф. использует сведения о «микроскопическом» строении тел и её поэтому наз. микроскопич. теорией.Поведение системы, состоящей из сравнительно небольшого числа ч-ц, можно описывать чисто механически. Иными словами, если в какой-то момент времени известны координаты и скорости всех ч-ц системы и известен закон их вз-ствия, то, решая ур-ния классич. механики, можно найти эти координаты и скорости в любой последующий момент времени и тем самым полностью определить состояние системы.Такой путь построения теории невозможен, однако, для макроскопич. тел, состоящих из очень большого гасла ч-ц. Напр., в 1 см3 газа при гемп-pe 0°С и давлении в 1 атм содержится примерно 2,7•1019 молекул. Невозможно ни решить ур-ния для такого числа молекул, ни получить информацию о координатах и скоростях всех молекул в нач. момент. Однако именно большое число ч-ц в макроскопич. телах приводит к появлению новых, статистич. закономерностей в поведении таких тел. Это поведение в широких пределах не зависит от конкретных нач. условий — от точных значении нач. координат и скоростей ч-ц. Важнейшее проявление этой независимости — известный из опыта факт, что система, изолированная от внеш. воздействий, с течением времени приходит в равновесное состояние, св-ва к-рого определяются только такими общими хар-ками нач. состояния, как число ч-ц, их суммарная энергия и т. п. (см. РАВНОВЕСИЕ ТЕРМОДИНАМИЧЕСКОЕ). Для теории, описывающей статистич. закономерности, характерно вычисление не точных значений разл. физ. величин для макроскопич. тел, а ср. значений этих величин по времени. Рассмотрим, напр., молекулы, находящиеся в нек-ром выделенном в газе достаточно большом, макроскопич. объёме. Число таких молекул с течением времени будет меняться из-за их движения. В равновесном состоянии изменение числа молекул в объёме будет носить хар-р беспорядочных колебаний — флуктуации — относительно нек-рого ср. значения. При большом числе ч-ц в объёме эти колебания будут малы по сравнению со ср. числом ч-ц, так что для хар-ки макроскопич. состояния достаточно знать именно это ср. значение.Функция распределения. Рассмотрим систему, состоящую из N ч-ц, для простоты считая, что ч-цы не имеют внутр. степеней свободы. Состояние такой системы определяется заданием 6N переменных — 3N координат qi; и 3N импульсов рi ч-ц (совокупность этих переменных сокращённо будем обозначать (р, q)). Вычислим ср. значение F=(p, q) по интервалу времени t нек-рой физ. величины F(p, q), являющейся ф-цией этих координат и импульсов (напр., энергии системы или числа ч-ц, находящихся в данном объёме). Для этого разобьём интервал (0, т) на s равных малых отрезков Dtа (а=1, 2, . . ., s). Тогда по определению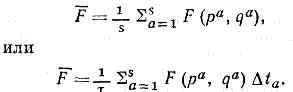 В пределе s®? (или Dа ®0) сумма переходит в интеграл:
В пределе s®? (или Dа ®0) сумма переходит в интеграл: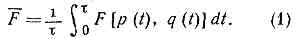 К важнейшему в С. ф. понятию ф-ции распределения можно естеств. образом прийти, если рассмотреть пр-во 6N измерений, соответствующих числу координат и импульсов ч-ц системы; оно наз. фазовым пространством. Каждому значению времени t соответствуют определ. значения всех q и р, т. е. нек-рая точка в фазовом пр-ве, изображающая состояние системы в данный момент времени t. Разобьём всё фазовое пр-во на элементы, размер к-рых dp, dq мал по сравнению с характерными для данного состояния системы значениями q и р, но ещё настолько велик, что в каждом из них находится много точек, изображающих состояние системы в разл, моменты времени t. Тогда число таких точек в элементе объёма будет примерно пропорц. величине этого объёма dpdq. Если обозначить коэфф. пропорциональности через w(p, q), то это число для элемента с центром в нек-рой точке (р, q) запишется в виде:w(p, q) dpdq, (2)где dpdq=dp1dqldp2dq2 . . . dp3N dq3N — объём выбранного элемента фазового пр-ва. Ср. значение (1) с учётом малости этих элементов объёма можно переписать какF=(t)=?F(p(t),q(t))w(p,q, t)dpdq (3)(интегрирование по координатам производится по всему объёму системы, по импульсам — от -? до +?). Ф-ция w(p, q, t) наз. функцией распределения по координатам и импульсам ч-ц. Она удовлетворяет условию нормировки:?w(p, q, t)dpdq =1. (4)Из (3) и (4) видно, что wdpdq есть не что иное, как вероятность нахождения системы в элементе dpdq фазового пр-ва.Ф-ции распределения можно дать и др. истолкование, если рассматривать одновременно большое число одинаковых систем и считать, что каждая точка в фазовом пр-ве изображает состояние одной такой системы. Тогда усреднение по времени в (1) можно понимать как усреднение по совокупности этих систем, или, как говорят, по статистическому ансамблю.Осн. положением С. ф. явл. утверждение о возможности определить ф-цию распределения из общих соображений (не решая ур-ний движения) для систем, находящихся в состоянии термодинамич. равновесия. Действительно, можно показать, что ф-ция распределения явл. интегралом движения системы, т. е. остаётся постоянной, если р и q меняются в соответствии с ур-ниями движения (см. ЛИУВИЛЛЯ ТЕОРЕМА).При движении замкнутой системы не меняется её энергия, поэтому все точки в фазовом пр-ве, изображающие состояние системы в разные моменты времени, должны лежать на нек-рой «гиперповерхности», соответствующей нач. значению энергии ?. Ур-ние этой поверхности имеет вид:Н(p, q)=?,где Н(р, q) — энергия системы, выраженная через координаты и импульсы, т. е. её Гамильтона функция.Существенно, что изменение состояния системы из мн. ч-ц носит крайне запутанный хар-р. Поэтому с течением времени точки, отвечающие определ. состояниям, распределяются по поверхности пост. энергии равномерно (см. ЭРГОДИЧЕСКАЯ ГИПОТЕЗА). Такое равномерное распределение по изоэнергетич. поверхности описывается ф-цией распределения вида:w(p, q)=A(d)(H(p,q)-?), (5)где d(Н(р, q)-?) — дельта-функция, отличная от нуля только при Н=?, т. е. на этой поверхности; А — постоянная, определяемая из условия нормировки (4). Ф-ция распределения (5), наз. микроканоническим распределением Гиббса, позволяет вычислять ср. значения всех физ. величин по ф-ле (3), не решая ур-ний движения.При выводе выражения (5) предполагалось, что единственная сохраняющаяся при движении системы величина, от к-рой зависит w, это энергия системы. Разумеется, сохраняются также импульс и момент импульса, но эти величины можно исключить, предположив, что рассматриваемая система заключена в неподвижный жёсткий ящик, к-рому ч-цы могут отдавать импульс и момент (т. о., макроскопич. импульс и момент импульса у системы отсутствуют). Наличие такого ящика не сказывается на статистич. св-вах системы.Фактически обычно рассматриваются не замкнутые системы, а макроскопич. тела, являющиеся малыми частями, или подсистемами, к.-л. замкнутой системы. Ф-ция распределения для подсистемы будет отлична от (5), но не будет зависеть от конкретного хар-ра остальной части системы — т. н. термостата. Поэтому ф-цию распределения подсистемы можно определить, считая, напр., что термостат обладает св-вами идеального газа. Чтобы найти ф-цию распределения для подсистемы, нужно проинтегрировать выражение (5) по координатам и импульсам ч-ц термостата. В результате получится:w(p, q)=e(F-H(p, q))kT. (6)Здесь F — свободная энергия. Коэфф. eF/kT определяется из условия нормировки (4):e-F/kT=Z=?e-H(p, q)/kTdpdq. (6, а)Распределение (6) наз. каноническим распределением Гиббса или просто канонич. распределением, а величина Z — статистическим интегралом. В отличие от микроканонич. распределения, энергия системы в канонич. распределении Гиббса не задана. Точки, изображающие состояния системы, сосредоточены в тонком, но конечной толщины слое, прилегающем к энергетич. поверхности, соответствующей ср. значению энергии, что означает возможность обмена энергией с термостатом. В остальном в применении к определённому макроскопич. телу оба распределения приводят по существу к одним и тем же результатам. Разница лишь в том, что при микроканонич. распределении все ср. значения оказываются выраженными через энергию тела, а при канонич. распределении — через темп-ру.Если тело состоит из двух невзаимодействующих частей 1 и 2 с ф-циями Гамильтона Н1 и H2, то для тела Н=Н1+Н2 и, согласно (6), ф-ция распределения тела разбивается на произведение ф-ций распределения для каждой из частей, так что эти части оказываются статистически независимыми.Ф-ла (6) справедлива для систем, к-рые описываются классич. механикой. В квантовой механике энергетич. спектр системы конечного объёма дискретен. Вероятность подсистеме находиться в состоянии с энергией ?n даётся ф-лой, аналогичной (6):
К важнейшему в С. ф. понятию ф-ции распределения можно естеств. образом прийти, если рассмотреть пр-во 6N измерений, соответствующих числу координат и импульсов ч-ц системы; оно наз. фазовым пространством. Каждому значению времени t соответствуют определ. значения всех q и р, т. е. нек-рая точка в фазовом пр-ве, изображающая состояние системы в данный момент времени t. Разобьём всё фазовое пр-во на элементы, размер к-рых dp, dq мал по сравнению с характерными для данного состояния системы значениями q и р, но ещё настолько велик, что в каждом из них находится много точек, изображающих состояние системы в разл, моменты времени t. Тогда число таких точек в элементе объёма будет примерно пропорц. величине этого объёма dpdq. Если обозначить коэфф. пропорциональности через w(p, q), то это число для элемента с центром в нек-рой точке (р, q) запишется в виде:w(p, q) dpdq, (2)где dpdq=dp1dqldp2dq2 . . . dp3N dq3N — объём выбранного элемента фазового пр-ва. Ср. значение (1) с учётом малости этих элементов объёма можно переписать какF=(t)=?F(p(t),q(t))w(p,q, t)dpdq (3)(интегрирование по координатам производится по всему объёму системы, по импульсам — от -? до +?). Ф-ция w(p, q, t) наз. функцией распределения по координатам и импульсам ч-ц. Она удовлетворяет условию нормировки:?w(p, q, t)dpdq =1. (4)Из (3) и (4) видно, что wdpdq есть не что иное, как вероятность нахождения системы в элементе dpdq фазового пр-ва.Ф-ции распределения можно дать и др. истолкование, если рассматривать одновременно большое число одинаковых систем и считать, что каждая точка в фазовом пр-ве изображает состояние одной такой системы. Тогда усреднение по времени в (1) можно понимать как усреднение по совокупности этих систем, или, как говорят, по статистическому ансамблю.Осн. положением С. ф. явл. утверждение о возможности определить ф-цию распределения из общих соображений (не решая ур-ний движения) для систем, находящихся в состоянии термодинамич. равновесия. Действительно, можно показать, что ф-ция распределения явл. интегралом движения системы, т. е. остаётся постоянной, если р и q меняются в соответствии с ур-ниями движения (см. ЛИУВИЛЛЯ ТЕОРЕМА).При движении замкнутой системы не меняется её энергия, поэтому все точки в фазовом пр-ве, изображающие состояние системы в разные моменты времени, должны лежать на нек-рой «гиперповерхности», соответствующей нач. значению энергии ?. Ур-ние этой поверхности имеет вид:Н(p, q)=?,где Н(р, q) — энергия системы, выраженная через координаты и импульсы, т. е. её Гамильтона функция.Существенно, что изменение состояния системы из мн. ч-ц носит крайне запутанный хар-р. Поэтому с течением времени точки, отвечающие определ. состояниям, распределяются по поверхности пост. энергии равномерно (см. ЭРГОДИЧЕСКАЯ ГИПОТЕЗА). Такое равномерное распределение по изоэнергетич. поверхности описывается ф-цией распределения вида:w(p, q)=A(d)(H(p,q)-?), (5)где d(Н(р, q)-?) — дельта-функция, отличная от нуля только при Н=?, т. е. на этой поверхности; А — постоянная, определяемая из условия нормировки (4). Ф-ция распределения (5), наз. микроканоническим распределением Гиббса, позволяет вычислять ср. значения всех физ. величин по ф-ле (3), не решая ур-ний движения.При выводе выражения (5) предполагалось, что единственная сохраняющаяся при движении системы величина, от к-рой зависит w, это энергия системы. Разумеется, сохраняются также импульс и момент импульса, но эти величины можно исключить, предположив, что рассматриваемая система заключена в неподвижный жёсткий ящик, к-рому ч-цы могут отдавать импульс и момент (т. о., макроскопич. импульс и момент импульса у системы отсутствуют). Наличие такого ящика не сказывается на статистич. св-вах системы.Фактически обычно рассматриваются не замкнутые системы, а макроскопич. тела, являющиеся малыми частями, или подсистемами, к.-л. замкнутой системы. Ф-ция распределения для подсистемы будет отлична от (5), но не будет зависеть от конкретного хар-ра остальной части системы — т. н. термостата. Поэтому ф-цию распределения подсистемы можно определить, считая, напр., что термостат обладает св-вами идеального газа. Чтобы найти ф-цию распределения для подсистемы, нужно проинтегрировать выражение (5) по координатам и импульсам ч-ц термостата. В результате получится:w(p, q)=e(F-H(p, q))kT. (6)Здесь F — свободная энергия. Коэфф. eF/kT определяется из условия нормировки (4):e-F/kT=Z=?e-H(p, q)/kTdpdq. (6, а)Распределение (6) наз. каноническим распределением Гиббса или просто канонич. распределением, а величина Z — статистическим интегралом. В отличие от микроканонич. распределения, энергия системы в канонич. распределении Гиббса не задана. Точки, изображающие состояния системы, сосредоточены в тонком, но конечной толщины слое, прилегающем к энергетич. поверхности, соответствующей ср. значению энергии, что означает возможность обмена энергией с термостатом. В остальном в применении к определённому макроскопич. телу оба распределения приводят по существу к одним и тем же результатам. Разница лишь в том, что при микроканонич. распределении все ср. значения оказываются выраженными через энергию тела, а при канонич. распределении — через темп-ру.Если тело состоит из двух невзаимодействующих частей 1 и 2 с ф-циями Гамильтона Н1 и H2, то для тела Н=Н1+Н2 и, согласно (6), ф-ция распределения тела разбивается на произведение ф-ций распределения для каждой из частей, так что эти части оказываются статистически независимыми.Ф-ла (6) справедлива для систем, к-рые описываются классич. механикой. В квантовой механике энергетич. спектр системы конечного объёма дискретен. Вероятность подсистеме находиться в состоянии с энергией ?n даётся ф-лой, аналогичной (6):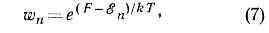 причём условие нормировки Snwn=1 можно переписать в виде:
причём условие нормировки Snwn=1 можно переписать в виде: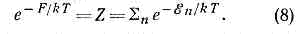 Величина Z наз. статистической суммой системы; сумма в выражении (8) берётся по всем возможным состояниям системы.Для системы, с достаточной точностью описываемой классич. механикой, в ф-ле (8) можно перейти от суммирования по состояниям к интегрированию по координатам и импульсам системы. При этом на каждое квант. состояние приходится в фазовом пр-ве «клетка» (или «ячейка») объёмом (2pћ)3N, где ћ — Планка постоянная. Иными словами, суммирование по и сводится к интегрированию по dpdq(2pћ)3N. Ввиду неразличимости (тождественности) одинаковых ч-ц в квант. механике их перестановка не меняет состояния системы. Поэтому, если интегрировать по всем р и q, необходимо поделить интеграл на число перестановок из N ч-ц, т. е. на N! Окончательно классич. предел статистич. суммы имеет вид:
Величина Z наз. статистической суммой системы; сумма в выражении (8) берётся по всем возможным состояниям системы.Для системы, с достаточной точностью описываемой классич. механикой, в ф-ле (8) можно перейти от суммирования по состояниям к интегрированию по координатам и импульсам системы. При этом на каждое квант. состояние приходится в фазовом пр-ве «клетка» (или «ячейка») объёмом (2pћ)3N, где ћ — Планка постоянная. Иными словами, суммирование по и сводится к интегрированию по dpdq(2pћ)3N. Ввиду неразличимости (тождественности) одинаковых ч-ц в квант. механике их перестановка не меняет состояния системы. Поэтому, если интегрировать по всем р и q, необходимо поделить интеграл на число перестановок из N ч-ц, т. е. на N! Окончательно классич. предел статистич. суммы имеет вид: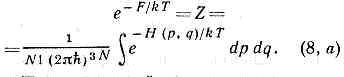 Приведённые ф-лы относятся к случаю, когда число ч-ц в подсистеме задано. Если выбрать в кач-ве подсистемы определ. элемент объёма всей системы, через поверхность к-рого ч-цы могут покидать подсистему и возвращаться в неё, то вероятность нахождения подсистемы в состоянии с энергией ? и числом ч-ц N даётся ф-лой большого канонического распределения Г и б б с а:
Приведённые ф-лы относятся к случаю, когда число ч-ц в подсистеме задано. Если выбрать в кач-ве подсистемы определ. элемент объёма всей системы, через поверхность к-рого ч-цы могут покидать подсистему и возвращаться в неё, то вероятность нахождения подсистемы в состоянии с энергией ? и числом ч-ц N даётся ф-лой большого канонического распределения Г и б б с а: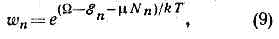 в к-рой параметр m — химический потенциал, определяющий ср. число ч-ц в подсистеме; величину W определяют из условия нормировки (см. ф-лу (11)).Статистическое истолкование термодинамики.Важнейший результат С. ф.— установление статистич. смысла термодинамич. величин. Это даёт возможность вывести законы термодинамики из осн. представлений С. ф. и вычислять термодинамич. величины для конкретных систем. Прежде всего термодинамическая внутренняя энергия отождествляется со ср. энергией системы. Первое начало термодинамики получает тогда очевидное истолкование как выражение закона сохранения энергии при движении составляющих тело ч-ц.Далее, пусть ф-ция Гамильтона системы зависит от нек-рого параметра l (координаты стенки сосуда, в к-рый заключена система, внеш. поля и т. п.). Тогда производная дН/дl будет обобщённой силой, соответствующей этому параметру, а величина (дH/дl)dl после усреднения даёт механич. работу, совершаемую над системой при изменении этого параметра. Если продифференцировать выражение ?»?Hwdpdq для ср. энергии системы с учётом ф-лы (6) и условия нормировки, считая переменными К и Т, то получится тождество
в к-рой параметр m — химический потенциал, определяющий ср. число ч-ц в подсистеме; величину W определяют из условия нормировки (см. ф-лу (11)).Статистическое истолкование термодинамики.Важнейший результат С. ф.— установление статистич. смысла термодинамич. величин. Это даёт возможность вывести законы термодинамики из осн. представлений С. ф. и вычислять термодинамич. величины для конкретных систем. Прежде всего термодинамическая внутренняя энергия отождествляется со ср. энергией системы. Первое начало термодинамики получает тогда очевидное истолкование как выражение закона сохранения энергии при движении составляющих тело ч-ц.Далее, пусть ф-ция Гамильтона системы зависит от нек-рого параметра l (координаты стенки сосуда, в к-рый заключена система, внеш. поля и т. п.). Тогда производная дН/дl будет обобщённой силой, соответствующей этому параметру, а величина (дH/дl)dl после усреднения даёт механич. работу, совершаемую над системой при изменении этого параметра. Если продифференцировать выражение ?»?Hwdpdq для ср. энергии системы с учётом ф-лы (6) и условия нормировки, считая переменными К и Т, то получится тождество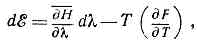 т. к. первый член справа равен ср. работе dA, совершаемой над телом, а последний член есть полученное телом кол-во теплоты. Сравнивая это выражение с соотношениемd?=dA+TdS,представляющим собой объединённую запись первого и второго начал термодинамики (см. ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ) для обратимых процессов, находим, что Т в (6) действительно равна абс. темп-ре тела, а производная дF/дТ — взятой с обратным знаком энтропии S. Это означает, что F — свободная энергия тела.Особое значение имеет статистич. истолкование энтропии, к-рое следует из ф-лы (8). Формально суммирование в этой ф-ле производится по всем состояниям с энергией ?n, но фактически ввиду малости флуктуации энергии в распределении Гиббса существенно лишь относительно небольшое их число с энергией вблизи ср. энергии. Число этих существенных состояний D=n можно определить, ограничив суммирование в (8) интервалом D=n, заменив ?n на ср. энергию ?= и вынеся экспоненту из-под знака суммы. Тогда сумма даст D=n и (8) примет вид:
т. к. первый член справа равен ср. работе dA, совершаемой над телом, а последний член есть полученное телом кол-во теплоты. Сравнивая это выражение с соотношениемd?=dA+TdS,представляющим собой объединённую запись первого и второго начал термодинамики (см. ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ) для обратимых процессов, находим, что Т в (6) действительно равна абс. темп-ре тела, а производная дF/дТ — взятой с обратным знаком энтропии S. Это означает, что F — свободная энергия тела.Особое значение имеет статистич. истолкование энтропии, к-рое следует из ф-лы (8). Формально суммирование в этой ф-ле производится по всем состояниям с энергией ?n, но фактически ввиду малости флуктуации энергии в распределении Гиббса существенно лишь относительно небольшое их число с энергией вблизи ср. энергии. Число этих существенных состояний D=n можно определить, ограничив суммирование в (8) интервалом D=n, заменив ?n на ср. энергию ?= и вынеся экспоненту из-под знака суммы. Тогда сумма даст D=n и (8) примет вид: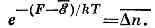 С другой стороны, согласно термодинамике, F=?-TS, что даёт связь энтропии с числом микроскопич. состояний D=n в данном макроскопич. состоянии, иначе говоря, со статистическим весом макроскопич. состояния, т. е. с его вероятностью:S=klnD=n. (10)При темп-ре абс. нуля любая система находится в определённом осн. состоянии, в к-ром D=n=1, S=0. Это утверждение выражает собой третье начало термодинамики. Здесь существенно, что для однозначного определения энтропии нужно пользоваться именно квант. ф-лой (8); в чисто классич. статистике энтропия определена только с точностью до произвольного слагаемого.Смысл энтропии как меры вероятности состояния сохраняется и по отношению к произвольным (не обязательно равновесным) состояниям. В состоянии равновесия энтропия имеет максимально возможное в данных внеш. условиях значение. Это означает, что равновесное состояние явл. состоянием с максимальным статистич. весом, наиболее вероятным состоянием. Процесс перехода системы из неравновесного состояния в равновесное есть процесс перехода из менее вероятных состояний в более вероятные; это выясняет статистич. смысл закона возрастания энтропии, согласно к-рому энтропия замкнутой системы может только увеличиваться.Ф-ла (8), связывающая свободную энергию F со статистич. суммой, явл. основой для вычисления термодинамич. величин методами С. ф. Она используется, в частности, для построения статистич. теории электрич. и магн. св-в в-ва. Напр., для вычисления магн. момента тела в магн. поле следует вычислить статистич. сумму и свободную энергию. Магн. момент тела даётся ф-лой: М =-(дF/дH), где Н— напряжённость I внеш. магн. поля.Аналогично (8) условие нормировки I в большом канонич. распределении I (9) определяет термодинамич. потенциал W:e-W/kT=Sne-(?n-mNn)/kT. (11)I Этот потенциал связан с F соотношением W=F-mN.Приложения С. ф. к изучению тех I или иных св-в конкретных систем I сводятся по существу к приближённому вычислению статистич. суммы I с учётом специфич. св-в системы, упрощающих расчёт.В случае газов таким упрощающим обстоятельством явл. их разрежённость, в силу к-рой вз-ствие между I молекулами играет относительно малую роль. В первом приближении можно вообще пренебречь этим вз-ствием и считать газ идеальным. Вз-ствие I же можно учесть как поправку. В результате. термодинамич. ф-ции удаётся представить в виде т. н. вириального разложения по малому параметру — плотности. В квант. статистике при низких темп-рах оказываются совершенно различными св-ва газов, состоящих из ч-ц с целым спином (бозонов) и полуцелым спином (фермионов), (см. ВЫРОЖДЕННЫЙ ГАЗ) .Приближённое вычисление статистич. суммы для крист. тв. тел основано на малости амплитуды колебаний атомов кристалла около их положений равновесия.В жидкостях вз-ствие между молекулами и амплитуды их колебаний нельзя считать малыми. Поэтому вычисление термодинамич. ф-ций жидкостей требует дополнительных упрощающих предположений и сложных расчётов.Ситуация упрощается при темп-рах, низких по сравнению с темп-рой вырождения жидкости. В этих условиях тепловое движение в жидкости можно рассматривать как появление в ней элем. возбуждений (квазичастиц), обладающих импульсом и энергией, связанными определённым дисперсии законом. При низких темп-рах эти квазичастицы образуют идеальный газ, что позволяет вычислить термодинамич. ф-ции в-в в соответствующих условиях. С теоретической точки зрения к таким квант. жидкостям относятся, кроме жидких при норм. давлении вплоть до абс. нуля темп-ры 4Не и 3Не, также электронная жидкость в металле, система спинов в ферромагнетиках и др.Большое значение имеет представляемая С. ф. возможность вычисления констант хим. равновесия, определяющих равновесные концентрации реагирующих в-в. Термодинамич. теория даёт условие равновесия в виде равенства нулю нек-рой комбинации хим. потенциалов этих в-в. В выражения для хим. потенциалов входит постоянная Планка, поэтому квант. эффекты существенны даже для реакций между классич. газами. Важным частным случаем ф-л хим. равновесия явл. Саха формула, определяющая равновесную степень ионизации газа. При решении задач квантовой С. ф., прежде всего при исследовании св-в квант. жидкостей, важное значение имеют методы квантовой теории поля, введённые в С. ф. сравнительно недавно. Осн. роль в этих методах играет ф-ция Грина макроскопич. системы, аналогичная ф-ции Грина в квант. теории поля. Полюсы этой ф-ции определяют закон дисперсии квазичастиц. Существует регулярный метод вычисления ф-ций Грина в виде ряда по степеням энергии вз-ствия между ч-цами. Каждый член этого ряда содержит многократные интегралы по энергиям и импульсам от ф-ций Грина невзаимодействующих ч-ц и может быть изображён графически в виде диаграмм, аналогичных Фейнмана диаграммам. Каждая из этих диаграмм имеет определённый физ. смысл, что позволяет отделить в бесконечном ряду члены, ответственные за интересующее явление, и просуммировать их. Существует также диаграммная техника для вычисления температурных ф-ций Грина, позволяющих вычислить термодинамич, величины без рассмотрения квазичастиц.При непрерывном изменении внеш. параметров (напр., давления или темп-ры) св-ва системы могут при нек-рых значениях параметров измениться скачкообразно, т. е. произойдёт фазовый переход. Фазовые переходы делятся на переходы I рода, сопровождающиеся выделением теплоты перехода и скачкообразным изменением объёма (к ним относится, напр., плавление), и II рода, в к-рых теплота перехода и скачок объёма отсутствуют (напр., переход жидкого гелия в сверхтекучее состояние). Статистич. теория фазовых переходов составляет важную, но ещё далёкую от завершения область С. ф. Наибольшую трудность для теор. исследования представляют при этом св-ва в-ва вблизи линии фазового перехода II рода и вблизи критической точки фазового перехода I рода. С матем. точки зрения термодинамич. ф-ции системы имеют здесь особенности. Вблизи этих точек происходят своеобразные критические явления. В то же время здесь аномально возрастают флуктуации, и рассмотренные выше приближённые методы С. ф. оказываются неприменимыми. Поэтому важную роль играет рассмотрение точно решаемых моделей, в к-рых есть переходы (напр., т. н. модель Изинга).В основе С. ф. лежит тот факт, что физ. величины, характеризующие макроскопич. тела в равновесных условиях, с большой точностью равны своим ср. значениям. Это равенство явл. всё же приближённым, в действительности все величины испытывают малые беспорядочные отклонения от ср. значений — флуктуации. Существование флуктуации имеет большое принципиальное значение, т. к. прямо доказывает статистич. хар-р термодинамич. закономерностей. Кроме того, флуктуации играют роль шума, мешающего физ. измерениям и ограничивающего их точность.С. ф. неравновесных процессов. Всё большее значение приобретает кинетика физическая — раздел С. ф., изучающий процессы в системах, находящихся в неравновесных состояниях. Здесь возможны две постановки вопроса. Во-первых, можно рассматривать систему в нек-ром неравновесном состоянии и следить за её переходом в состояние равновесия. Во-вторых, можно рассматривать систему, неравновесное состояние к-рой поддерживается внеш. условиями, напр. тело, в к-ром задан градиент темп-ры, протекает электрич. ток и т. п., или тело, находящееся в перемен. внеш. поле.Если отклонение от равновесия мало, неравновесные св-ва системы описываются т. н. кинетическими коэффициентами. Примерами явл. коэфф. вязкости, теплопроводности и диффузии, электропроводность металлов и т. п. Эти величины удовлетворяют принципу симметрии кинетич. коэффициентов, выражающему симметрию ур-ний механики относительно изменения знака времени (см. ОНСАГЕРА ТЕОРЕМА). В силу этого принципа, напр., электропроводность кристалла описывается симметричным тензором.Описание сильно неравновесных состояний, а также вычисление кинетич. коэфф. производятся при помощи кинетического уравнения. Оно представляет собой интегродифф. ур-ние для одночастичной ф-ции распределения, к-рая получается из введённой равенством (2) N-частичной ф-ции распределения интегрированием по координатам и импульсам всех ч-ц, кроме одной. В квант. случае вместо одночастичной ф-ции распределения пользуются одночастичной матрицей плотности, или статистич. оператором. Такое замкнутое, т. е. не содержащее др. величин, ур-ние невозможно получить в общем виде. При его выводе необходимо использовать малые параметры, имеющиеся в данной конкретной задаче. Важнейшим примером явл. кинетическое уравнение Больцмана, описывающее установление равновесия в газе за счёт столкновений между молекулами. Конкретный вид этого ур-ния зависит от коэфф. сечения рассеяния молекул друг на друге. Если это сечение известно, то можно вычислить кинетич. коэфф. газа. Ур-ние Больцмана учитывает только парные столкновения между молекулами и описывает только первый неисчезающий член разложения этих коэфф. по плотности газа. Удалось найти и более точное ур-ние, учитывающее также тройные столкновения, что позволило вычислить следующий член разложения.Особую проблему представляет вывод кинетич. ур-ния для плазмы. Из-за медл. убывания кулоновских сил с расстоянием даже при парных столкновениях существенно влияние остальных ч-ц.Неравновесные состояния тв. тел и квант. жидкостей можно при низких темп-рах рассматривать как неравновесные состояния газа соответствующих квазичастиц. Поэтому кинетич. процессы в таких системах описываются кинетич. ур-ниями для квазичастиц, учитывающими столкновения между ними и процессы их взаимного превращения.Новые возможности открыло применение в физ. кинетике методов квант. теории поля. Кинетич. коэфф. системы можно выразить через её ф-цию Грина, для к-рой существует общий способ вычисления при помощи диаграмм, без введения квазичастиц. Это позволяет в ряде случаев исследовать неравновесные св-ва систем, даже когда не выполняются условия применимости кинетич. ур-ния.Основные вехи развития С. ф.С. ф. целиком основана на представлениях об ат. строении материи. Поэтому нач. период развития С. ф. совпадает с развитием атомистич. представлений (см. АТОМНАЯ ФИЗИКА). Развитие С. ф. как раздела теор. физики началось в сер. 19 в. В 1859 англ. физик Дж. Максвелл определил ф-цию распределения молекул газа по скоростям. В 1860—70 нем. физик Р. Клаузиус ввёл понятие длины свободного пробега и связал её с вязкостью и теплопроводностью газа. Примерно в то же время австр. физик Л. Больцман обобщил распределение Максвелла на случай, когда газ находится во внеш. поле, доказал теорему о распределении энергии по степеням свободы, вывел кинетич. ур-ние, дал статистич. истолкование энтропии и показал, что закон её возрастания явл. следствием кинетич. ур-ния. Нем. физик П. Друде (1900) и голл. физик X. Лоренц (1904) применили кинетич. теорию для объяснения св-в металлов. Построение классич. С. ф. было завершено к 1902 в работах амер. физика Дж. У. Гиббса. Теория флуктуации была развита в 1905—06 в работах польск. физика М. Смолуховского и А. Эйнштейна. В 1900 нем. физик М. Планк вывел закон распределения энергии в спектре излучения чёрного тела, положив начало развитию как квант. механики, так и квантовой С. ф. В 1907 Эйнштейн применил квант. теорию для вычисления теплоёмкости тв. тел, а нем. физик В. Нернст (1911) — теплоёмкости газов.В 1924 инд. физик Ш. Бозе нашёл распределение по импульсам световых квантов и связал его с распределением Планка. Эйнштейн обобщил распределение Бозе на газы с заданным числом ч-ц. Итал. физик Э. Ферми в 1925 получил ф-цию распределения ч-ц, подчиняющихся принципу Паули, а англ. физик П. А. М. Дирак установил связь этого распределения и распределения Бозе — Эйнштейна с матем. аппаратом квант. механики. Дальнейшее развитие С. ф. в 20 в. шло под знаком приложения её осн. принципов к исследованию конкретных проблем.
С другой стороны, согласно термодинамике, F=?-TS, что даёт связь энтропии с числом микроскопич. состояний D=n в данном макроскопич. состоянии, иначе говоря, со статистическим весом макроскопич. состояния, т. е. с его вероятностью:S=klnD=n. (10)При темп-ре абс. нуля любая система находится в определённом осн. состоянии, в к-ром D=n=1, S=0. Это утверждение выражает собой третье начало термодинамики. Здесь существенно, что для однозначного определения энтропии нужно пользоваться именно квант. ф-лой (8); в чисто классич. статистике энтропия определена только с точностью до произвольного слагаемого.Смысл энтропии как меры вероятности состояния сохраняется и по отношению к произвольным (не обязательно равновесным) состояниям. В состоянии равновесия энтропия имеет максимально возможное в данных внеш. условиях значение. Это означает, что равновесное состояние явл. состоянием с максимальным статистич. весом, наиболее вероятным состоянием. Процесс перехода системы из неравновесного состояния в равновесное есть процесс перехода из менее вероятных состояний в более вероятные; это выясняет статистич. смысл закона возрастания энтропии, согласно к-рому энтропия замкнутой системы может только увеличиваться.Ф-ла (8), связывающая свободную энергию F со статистич. суммой, явл. основой для вычисления термодинамич. величин методами С. ф. Она используется, в частности, для построения статистич. теории электрич. и магн. св-в в-ва. Напр., для вычисления магн. момента тела в магн. поле следует вычислить статистич. сумму и свободную энергию. Магн. момент тела даётся ф-лой: М =-(дF/дH), где Н— напряжённость I внеш. магн. поля.Аналогично (8) условие нормировки I в большом канонич. распределении I (9) определяет термодинамич. потенциал W:e-W/kT=Sne-(?n-mNn)/kT. (11)I Этот потенциал связан с F соотношением W=F-mN.Приложения С. ф. к изучению тех I или иных св-в конкретных систем I сводятся по существу к приближённому вычислению статистич. суммы I с учётом специфич. св-в системы, упрощающих расчёт.В случае газов таким упрощающим обстоятельством явл. их разрежённость, в силу к-рой вз-ствие между I молекулами играет относительно малую роль. В первом приближении можно вообще пренебречь этим вз-ствием и считать газ идеальным. Вз-ствие I же можно учесть как поправку. В результате. термодинамич. ф-ции удаётся представить в виде т. н. вириального разложения по малому параметру — плотности. В квант. статистике при низких темп-рах оказываются совершенно различными св-ва газов, состоящих из ч-ц с целым спином (бозонов) и полуцелым спином (фермионов), (см. ВЫРОЖДЕННЫЙ ГАЗ) .Приближённое вычисление статистич. суммы для крист. тв. тел основано на малости амплитуды колебаний атомов кристалла около их положений равновесия.В жидкостях вз-ствие между молекулами и амплитуды их колебаний нельзя считать малыми. Поэтому вычисление термодинамич. ф-ций жидкостей требует дополнительных упрощающих предположений и сложных расчётов.Ситуация упрощается при темп-рах, низких по сравнению с темп-рой вырождения жидкости. В этих условиях тепловое движение в жидкости можно рассматривать как появление в ней элем. возбуждений (квазичастиц), обладающих импульсом и энергией, связанными определённым дисперсии законом. При низких темп-рах эти квазичастицы образуют идеальный газ, что позволяет вычислить термодинамич. ф-ции в-в в соответствующих условиях. С теоретической точки зрения к таким квант. жидкостям относятся, кроме жидких при норм. давлении вплоть до абс. нуля темп-ры 4Не и 3Не, также электронная жидкость в металле, система спинов в ферромагнетиках и др.Большое значение имеет представляемая С. ф. возможность вычисления констант хим. равновесия, определяющих равновесные концентрации реагирующих в-в. Термодинамич. теория даёт условие равновесия в виде равенства нулю нек-рой комбинации хим. потенциалов этих в-в. В выражения для хим. потенциалов входит постоянная Планка, поэтому квант. эффекты существенны даже для реакций между классич. газами. Важным частным случаем ф-л хим. равновесия явл. Саха формула, определяющая равновесную степень ионизации газа. При решении задач квантовой С. ф., прежде всего при исследовании св-в квант. жидкостей, важное значение имеют методы квантовой теории поля, введённые в С. ф. сравнительно недавно. Осн. роль в этих методах играет ф-ция Грина макроскопич. системы, аналогичная ф-ции Грина в квант. теории поля. Полюсы этой ф-ции определяют закон дисперсии квазичастиц. Существует регулярный метод вычисления ф-ций Грина в виде ряда по степеням энергии вз-ствия между ч-цами. Каждый член этого ряда содержит многократные интегралы по энергиям и импульсам от ф-ций Грина невзаимодействующих ч-ц и может быть изображён графически в виде диаграмм, аналогичных Фейнмана диаграммам. Каждая из этих диаграмм имеет определённый физ. смысл, что позволяет отделить в бесконечном ряду члены, ответственные за интересующее явление, и просуммировать их. Существует также диаграммная техника для вычисления температурных ф-ций Грина, позволяющих вычислить термодинамич, величины без рассмотрения квазичастиц.При непрерывном изменении внеш. параметров (напр., давления или темп-ры) св-ва системы могут при нек-рых значениях параметров измениться скачкообразно, т. е. произойдёт фазовый переход. Фазовые переходы делятся на переходы I рода, сопровождающиеся выделением теплоты перехода и скачкообразным изменением объёма (к ним относится, напр., плавление), и II рода, в к-рых теплота перехода и скачок объёма отсутствуют (напр., переход жидкого гелия в сверхтекучее состояние). Статистич. теория фазовых переходов составляет важную, но ещё далёкую от завершения область С. ф. Наибольшую трудность для теор. исследования представляют при этом св-ва в-ва вблизи линии фазового перехода II рода и вблизи критической точки фазового перехода I рода. С матем. точки зрения термодинамич. ф-ции системы имеют здесь особенности. Вблизи этих точек происходят своеобразные критические явления. В то же время здесь аномально возрастают флуктуации, и рассмотренные выше приближённые методы С. ф. оказываются неприменимыми. Поэтому важную роль играет рассмотрение точно решаемых моделей, в к-рых есть переходы (напр., т. н. модель Изинга).В основе С. ф. лежит тот факт, что физ. величины, характеризующие макроскопич. тела в равновесных условиях, с большой точностью равны своим ср. значениям. Это равенство явл. всё же приближённым, в действительности все величины испытывают малые беспорядочные отклонения от ср. значений — флуктуации. Существование флуктуации имеет большое принципиальное значение, т. к. прямо доказывает статистич. хар-р термодинамич. закономерностей. Кроме того, флуктуации играют роль шума, мешающего физ. измерениям и ограничивающего их точность.С. ф. неравновесных процессов. Всё большее значение приобретает кинетика физическая — раздел С. ф., изучающий процессы в системах, находящихся в неравновесных состояниях. Здесь возможны две постановки вопроса. Во-первых, можно рассматривать систему в нек-ром неравновесном состоянии и следить за её переходом в состояние равновесия. Во-вторых, можно рассматривать систему, неравновесное состояние к-рой поддерживается внеш. условиями, напр. тело, в к-ром задан градиент темп-ры, протекает электрич. ток и т. п., или тело, находящееся в перемен. внеш. поле.Если отклонение от равновесия мало, неравновесные св-ва системы описываются т. н. кинетическими коэффициентами. Примерами явл. коэфф. вязкости, теплопроводности и диффузии, электропроводность металлов и т. п. Эти величины удовлетворяют принципу симметрии кинетич. коэффициентов, выражающему симметрию ур-ний механики относительно изменения знака времени (см. ОНСАГЕРА ТЕОРЕМА). В силу этого принципа, напр., электропроводность кристалла описывается симметричным тензором.Описание сильно неравновесных состояний, а также вычисление кинетич. коэфф. производятся при помощи кинетического уравнения. Оно представляет собой интегродифф. ур-ние для одночастичной ф-ции распределения, к-рая получается из введённой равенством (2) N-частичной ф-ции распределения интегрированием по координатам и импульсам всех ч-ц, кроме одной. В квант. случае вместо одночастичной ф-ции распределения пользуются одночастичной матрицей плотности, или статистич. оператором. Такое замкнутое, т. е. не содержащее др. величин, ур-ние невозможно получить в общем виде. При его выводе необходимо использовать малые параметры, имеющиеся в данной конкретной задаче. Важнейшим примером явл. кинетическое уравнение Больцмана, описывающее установление равновесия в газе за счёт столкновений между молекулами. Конкретный вид этого ур-ния зависит от коэфф. сечения рассеяния молекул друг на друге. Если это сечение известно, то можно вычислить кинетич. коэфф. газа. Ур-ние Больцмана учитывает только парные столкновения между молекулами и описывает только первый неисчезающий член разложения этих коэфф. по плотности газа. Удалось найти и более точное ур-ние, учитывающее также тройные столкновения, что позволило вычислить следующий член разложения.Особую проблему представляет вывод кинетич. ур-ния для плазмы. Из-за медл. убывания кулоновских сил с расстоянием даже при парных столкновениях существенно влияние остальных ч-ц.Неравновесные состояния тв. тел и квант. жидкостей можно при низких темп-рах рассматривать как неравновесные состояния газа соответствующих квазичастиц. Поэтому кинетич. процессы в таких системах описываются кинетич. ур-ниями для квазичастиц, учитывающими столкновения между ними и процессы их взаимного превращения.Новые возможности открыло применение в физ. кинетике методов квант. теории поля. Кинетич. коэфф. системы можно выразить через её ф-цию Грина, для к-рой существует общий способ вычисления при помощи диаграмм, без введения квазичастиц. Это позволяет в ряде случаев исследовать неравновесные св-ва систем, даже когда не выполняются условия применимости кинетич. ур-ния.Основные вехи развития С. ф.С. ф. целиком основана на представлениях об ат. строении материи. Поэтому нач. период развития С. ф. совпадает с развитием атомистич. представлений (см. АТОМНАЯ ФИЗИКА). Развитие С. ф. как раздела теор. физики началось в сер. 19 в. В 1859 англ. физик Дж. Максвелл определил ф-цию распределения молекул газа по скоростям. В 1860—70 нем. физик Р. Клаузиус ввёл понятие длины свободного пробега и связал её с вязкостью и теплопроводностью газа. Примерно в то же время австр. физик Л. Больцман обобщил распределение Максвелла на случай, когда газ находится во внеш. поле, доказал теорему о распределении энергии по степеням свободы, вывел кинетич. ур-ние, дал статистич. истолкование энтропии и показал, что закон её возрастания явл. следствием кинетич. ур-ния. Нем. физик П. Друде (1900) и голл. физик X. Лоренц (1904) применили кинетич. теорию для объяснения св-в металлов. Построение классич. С. ф. было завершено к 1902 в работах амер. физика Дж. У. Гиббса. Теория флуктуации была развита в 1905—06 в работах польск. физика М. Смолуховского и А. Эйнштейна. В 1900 нем. физик М. Планк вывел закон распределения энергии в спектре излучения чёрного тела, положив начало развитию как квант. механики, так и квантовой С. ф. В 1907 Эйнштейн применил квант. теорию для вычисления теплоёмкости тв. тел, а нем. физик В. Нернст (1911) — теплоёмкости газов.В 1924 инд. физик Ш. Бозе нашёл распределение по импульсам световых квантов и связал его с распределением Планка. Эйнштейн обобщил распределение Бозе на газы с заданным числом ч-ц. Итал. физик Э. Ферми в 1925 получил ф-цию распределения ч-ц, подчиняющихся принципу Паули, а англ. физик П. А. М. Дирак установил связь этого распределения и распределения Бозе — Эйнштейна с матем. аппаратом квант. механики. Дальнейшее развитие С. ф. в 20 в. шло под знаком приложения её осн. принципов к исследованию конкретных проблем.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- СТАТИСТИЧЕСКАЯ ФИЗИКА
-
- раздел физики, задача к-рого - выразитьсвойства макроскопич. тел, т. е. систем, состоящих из очень большого числаодинаковых частиц (молекул, атомов, электронов и т. д.), через свойстваэтих частиц и взаимодействие между ними.
Т. о., в С. ф. используются сведения о «микроскопическом» строении тел, поэтому С. ф. является микроскопич. теорией. В этом её отличие от др. разделовфизики, также изучающих макроскопич. тела: термодинамики, механики и электродинамикисплошных сред. При решении конкретных задач методами этих дисциплин в соответствующиеур-ния всегда входят неизвестные параметры или ф-ции, характеризующие данноетело. Все эти зависимости и параметры можно определять экспериментально, поэтому методы, о к-рых идёт речь, наз. феноменологическими. С. ф. позволяет, по крайней мере в принципе, а во мн. случаях и фактически, вычислить этивеличины.
Если в какой-то момент времени заданы координаты и скорости всех частицтела и известен закон их взаимодействия, то из ур-ний механики можно былобы найти координаты и скорости в любой последующий момент времени и темсамым полностью определить состояние тела. Такая же ситуация имеет местои в квантовой механике: зная начальную волновую ф-цию системы, можно, решаяур-ние Шрёдингера, найти волновую ф-цию, определяющую состояние системыво все будущие моменты времени.
Реально такой путь построения микроскопич. теории невозможен, т. к. число частиц в макроскопич. телах очень велико, а нач. координаты и скоростимолекул неизвестны. Однако именно большое число частиц в макроскопич. телахприводит к появлению новых (статистич.) закономерностей в поведении такихтел. Эти закономерности выявляются после соответствующего ограничения задачтеории. Характеризующие макроскопич. тела параметры испытывают с течениемвремени беспорядочные малые колебания (флуктуации) относительно нек-рыхср. значений. Задачей теории является вычисление этих ср. значений, а неточных значений параметров в данный момент времени. Наличие статистич. закономерностей выражается в том, что поведение ср. значений в широкихпределах не зависит от конкретных нач. условий (от точных значений нач. координат и скоростей частиц). Важнейшее проявление этой закономерности- известный из опыта факт, что система, изолированная от внеш. воздействий, с течением времени приходит в нек-рое равновесное состояние (термодинамич. равновесие), свойства к-рого определяются только такими общими характеристикаминач. состояния, как число частиц, их суммарная энергия и т. п. (см. Равновесиетермодинамическое). Процесс перехода системы в равновесное состояниеназ. релаксацией, а характерное время этого процесса - временемрелаксации.
Функция распределения. Рассмотрим систему, состоящую из N частиц, для простоты считая, что частицы не имеют внутр. степеней свободы. Такаясистема описывается заданием 6N переменных: 3N координат xi и 3N импульсов р i частиц, совокупность этих переменных сокращённо обозначим ( р, х).
Понятие функции распределения естественно возникает, если рассмотретьпространство 6N измерений, соответственно значениям координат иимпульсов частиц; оно наз. фазовым пространством. Каждому моментувремени t соответствуют определ. значения всех х и р, т. е. нек-рая точка в фазовом пространстве, изображающая состояниесистемы в данный момент. С течением времени значения х и р меняются, так что точка в фазовом пространстве движется.
Вычислим ср. значение
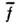 по заданному интервалу времени нек-рой ф-ции координат и импульсов f(x,p). Для этого выберем на этом интервале s моментов времени
по заданному интервалу времени нек-рой ф-ции координат и импульсов f(x,p). Для этого выберем на этом интервале s моментов времени 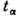 ,разделённых равными промежутками, им соответствует s точек в фазовом пространстве. Разобьём всё фазовое пространство на элементы, размер к-рых мал по сравнениюс характерными для системы значениями х и р, но ещё настолько велик, что в каждом из них находится много точек, изображающих состояние системыв моменты времени
,разделённых равными промежутками, им соответствует s точек в фазовом пространстве. Разобьём всё фазовое пространство на элементы, размер к-рых мал по сравнениюс характерными для системы значениями х и р, но ещё настолько велик, что в каждом из них находится много точек, изображающих состояние системыв моменты времени 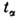 .Тогда число таких точек в элементе объёма будет примерно пропорциональновеличине этого объёма dxdp. Если обозначить коэф. пропорциональности, т. е. плотность числа точек в пространстве, через sw(x,p), то числоточек для элемента с центром в нек-рой точке ( х, р )запишется в виде:
.Тогда число таких точек в элементе объёма будет примерно пропорциональновеличине этого объёма dxdp. Если обозначить коэф. пропорциональности, т. е. плотность числа точек в пространстве, через sw(x,p), то числоточек для элемента с центром в нек-рой точке ( х, р )запишется в виде: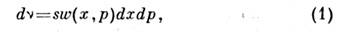
где dxdp= dx1dp1dx2dp2...dx3Ndp3N- объём выбранного элемента фазового пространства. Ср. значение
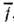 ,вычисленное по определению
,вычисленное по определению 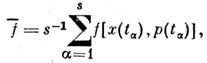
с учётом малости этих элементов объёма можно переписать как
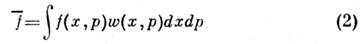
(интегрирование по координатам производится по всему объёму системы, по импульсам - от
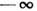 до
до 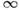 ). Ф-ция w(x,p )наз. ф-цией распределения по координатам и импульсам частиц. Поскольку полное число выбранных точек равно s, ф-ция w удовлетворяетусловию нормировки:
). Ф-ция w(x,p )наз. ф-цией распределения по координатам и импульсам частиц. Поскольку полное число выбранных точек равно s, ф-ция w удовлетворяетусловию нормировки: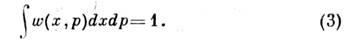
Из (2) и (3) видно, что wdxdp можно рассматривать как вероятностьтого, что система находится в элементе dxdp фазового пространства.
Если система не находится в состоянии термодинамич. равновесия, ф-цияраспределения зависит, кроме х и р, от времени t. В этомслучае следует считать, что интервал усреднения мал по сравнению со временемрелаксации.
Введённой таким образом ф-ции распределения можно дать и др. истолкование. Для этого рассмотрим одновременно большое число одинаковых систем и примем, что каждая точка в фазовом пространстве изображает состояние одной такойсистемы. Тогда усреднение по времени можно понимать как усреднение по совокупностиэтих систем, или, как говорят, по статистическому ансамблю.
Распределения Гиббса. Проведённые до сих пор рассуждения носили формальныйхарактер, т. к. нахождение ф-ции распределения, согласно (1), требует знаниявсех х и р во все моменты времени, т. е. решения ур-ний движенияс соответствующими нач. условиями. Осн. положением С. ф. является утверждениео возможности из общих соображений определить эту ф-цию для системы, находящейсяв состоянии термодинамич. равновесия. Прежде всего, исходя из сохранениячисла частиц при движении, можно показать, что ф-ция распределения являетсяинтегралом движения системы (см. Лиувилля теорема).
При движении замкнутой системы её энергия не меняется, поэтому все точкив фазовом пространстве, изображающие состояние системы в разные моментывремени, должны лежать на нек-рой гиперповерхности, соответствующей нач. значению энергии Е. Ур-ние этой поверхности имеет вид Н(х, р)= Е, где Н(х, р) - Гамильтона функция системы. Движение системыиз мн. частиц носит крайне запутанный характер, поэтому с течением времениточки, описывающие состояние, распределятся по поверхности пост. энергииравномерно (см. также Эргодическая гипотеза). Такое равномерноераспределение описывают ф-цией распределения
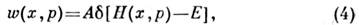
где
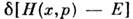 - дельта-функция, отличная от нуля только при Н = Е, А - постоянная, определяемая из условия нормировки (3). Ф-ция распределения (4), соответствующая микроканоническому распределению Гиббса, позволяет вычислять ср. значения всех физ. величин по ф-ле (2), не решая ур-ний движения.
- дельта-функция, отличная от нуля только при Н = Е, А - постоянная, определяемая из условия нормировки (3). Ф-ция распределения (4), соответствующая микроканоническому распределению Гиббса, позволяет вычислять ср. значения всех физ. величин по ф-ле (2), не решая ур-ний движения.При выводе выражения (4) предполагалось, что единственная сохраняющаясявеличина, от к-рой зависит w,- это энергия системы. Разумеется, сохраняются также импульс и момент импульса, но эти величины можно исключить, предположив, что рассматриваемое тело заключено в неподвижный ящик, к-ромучастицы могут отдавать импульс и момент.
Фактически в С. ф. обычно рассматривают не замкнутые системы, а макроскопич. тела, являющиеся малыми макроскопич. частями, или подсистемами, к.-л. замкнутойсистемы. Ф-ция распределения для подсистемы отлична от (4), но не зависитот конкретного вида остальной части системы, т. н. термостата. Для определенияф-ции распределения подсистемы необходимо проинтегрировать ф-лу (4) поимпульсам и координатам частиц термостата. Такое интегрирование можно произвести, учитывая малость энергии подсистемы по сравнению с энергией термостата. В результате для ф-ции распределения подсистемы получается выражение
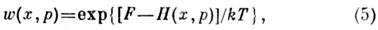
величина Т в этой ф-ле имеет смысл темп-ры. Нормировочный коэф.
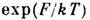 определяется из условия нормировки (3):
определяется из условия нормировки (3):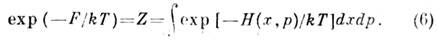
Распределение (а) наз. каноническим распределением Гиббса илипросто канонич. распределением (см. Гиббса распределения), а величинаZ - статистич. интегралом. В отличие от микроканонич. распределения, вканонич. распределении энергия системы не задана. Состояния системы сосредоточеныв тонком слое конечной толщины вокруг энергетич. поверхности, соответствующейср. значению энергии, что означает возможность обмена энергией с термостатом. В остальном в применении к определ. макроскопич. телу оба распределенияприводят по существу к одним и тем же результатам. Различие состоит лишьв том, что при использовании микроканонич. распределения все ср. значенияоказываются выраженными через энергию тела, а при использовании канонич. распределения- через темп-ру.
Если тело состоит из двух невзаимодействующих частей 1 и 2 с ф-циямиГамильтона Н 1 и Н 2, то для всего тела Н = H1 + H2 и, согласно (5), ф-цияраспределения тела разбивается на произведение ф-ций распределения длякаждой из частей, так что эти части оказываются статистически независимыми. Это требование вместе с теоремой Лиувилля можно положить в основу выводараспределения Гиббса, не обращаясь к микроканонич. распределению.
До сих пор мы говорили о системах, описываемых классич. механикой. Вквантовой механике роль ф-ции распределения играет статистический оператор (статистич. матрица)
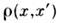 . Ср. значения физ. величин выражаются через него ф-лой, аналогичной ф-ле(2) классич. теории:
. Ср. значения физ. величин выражаются через него ф-лой, аналогичной ф-ле(2) классич. теории: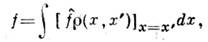
где
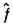 -квантовомеханич. оператор величины f, действующий на координаты х. Характерной особенностью квантовой механики является дискретностьэнергетич. спектра системы коночного объёма. Вероятность того, что подсистеманаходится в квантовом состоянии с энергией Е п, в тормодинамич. равновесии определяется ф-лой, аналогичной (5):
-квантовомеханич. оператор величины f, действующий на координаты х. Характерной особенностью квантовой механики является дискретностьэнергетич. спектра системы коночного объёма. Вероятность того, что подсистеманаходится в квантовом состоянии с энергией Е п, в тормодинамич. равновесии определяется ф-лой, аналогичной (5):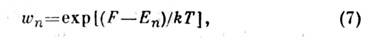
причём условие нормировки
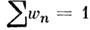 можно переписать в виде:
можно переписать в виде: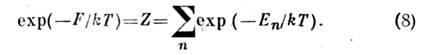
Величина Z наз. статистической суммой системы; сумма ввыражении (8) берётся по всем состояниям системы. В операторном виде ф-лу(8) можно переписать как
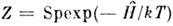 , где
, где 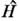 - гамильтониан подсистемы.
- гамильтониан подсистемы.Энергетич. спектр макроскопич. тела фактически является очень густым, поэтому целесообразно в ф-ле (8) перейти от суммирования к интегрированию, введя плотность числа состояний g(E), так что g(E)dE естьчисло состояний в интервале энергий dE, тогда
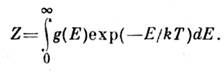
Статистич. матрица в состоянии равновесия имеет вид:
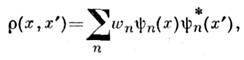
где
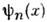 - волновая ф-ция стационарного состояния подсистемы с энергией Е п.
- волновая ф-ция стационарного состояния подсистемы с энергией Е п.Для системы, с достаточной точностью описывающейся классич. механикой, в ф-ле (8) можно перейти от суммирования но состояниям к интегрированиюпо координатам и импульсам системы. При этом на каждое квантовое состояниеприходится в фазовом пространстве «ячейка» объёмом
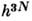 .Иными словами, суммирование по п сводится к интегрированию по
.Иными словами, суммирование по п сводится к интегрированию по 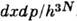 . Следует также учесть, что ввиду тождественности частиц в квантовой механикепри их перестановке состояние системы не меняется. Поэтому, если интегрироватьпо всем х и р, необходимо поделить интеграл на число перестановокиз N частиц, т. е. на N!. Окончательно классич. предел длястатистич. суммы имеет следующий вид:
. Следует также учесть, что ввиду тождественности частиц в квантовой механикепри их перестановке состояние системы не меняется. Поэтому, если интегрироватьпо всем х и р, необходимо поделить интеграл на число перестановокиз N частиц, т. е. на N!. Окончательно классич. предел длястатистич. суммы имеет следующий вид: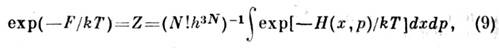
отличающийся множителем от чисто классич. выражения (6), что приводитк дополнит. слагаемому в ф-ле для F.
Приведённые ф-лы относятся к случаю, когда число частиц в подсистемезадано. Если выбрать в качестве подсистемы определ. элемент объёма всейсистемы, через поверхность к-рого частицы могут покидать подсистему и возвращатьсяв неё, то вероятность нахождения подсистемы в состоянии с энергией Е п и числом частиц Nn определяется большим каноническимраспределением Гиббса:
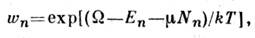
в к-ром имеется дополнит. параметр
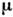 - хим. потенциал, определяющий ср. число частиц в подсистеме, а величина
- хим. потенциал, определяющий ср. число частиц в подсистеме, а величина 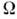 определяется из условия нормировки:
определяется из условия нормировки: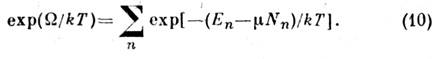
Статистическое истолкование термодинамики. Важнейший результат С. ф.-установление статистич. смысла термодинамич. величин. Это даёт возможностьвывести законы термодинамики из осн. представлений С. ф. и вычислятьтермодинамич. величины для конкретных систем. Прежде всего термодинамич. внутр. энергия отождествляется со ср. энергией системы. Первое началотермодинамики получает тогда истолкование как выражение закона сохраненияэнергии при движении составляющих тело частиц.
Далее, пусть гамильтониан
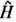 системы зависит от нек-рого параметра
системы зависит от нек-рого параметра 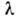 (координаты стенки сосуда, в к-рый заключена система, внеш. поля и т. п.).Тогда производная
(координаты стенки сосуда, в к-рый заключена система, внеш. поля и т. п.).Тогда производная 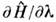 является оператором обобщённой силы, соответствующей этому параметру, авеличина
является оператором обобщённой силы, соответствующей этому параметру, авеличина 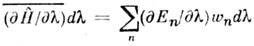 равна механич. работе, совершаемой над системой при изменении этого параметра. Если продифференцировать выражение
равна механич. работе, совершаемой над системой при изменении этого параметра. Если продифференцировать выражение 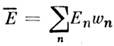
для ср. энергии
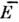 системыс учётом ф-лы (7) и условия нормировки и считать
системыс учётом ф-лы (7) и условия нормировки и считать 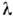 и Т переменными, а величину F - ф-цией этих переменных, тополучим тождество:
и Т переменными, а величину F - ф-цией этих переменных, тополучим тождество: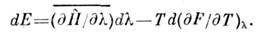
Как отмечено выше, первое слагаемое справа равно ср. работе dA , совершаемой над телом, тогда второе слагаемое представляет получаемуютелом теплоту. Сравнивая это выражение с соотношением
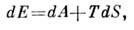 представляющим собой объединённую запись 1-го и 2-го начала термодинамики(см. Второе начало термодинамики )для обратимых процессов, находим, что величина Т в ф-ле (7) равна абс. темп-ре тела, а производная dF/дТ - взятой с обратным знаком энтропии S. Следовательно,F - свободная энергия тела, что и выявляет её статистич. смысл. Аналогично условию нормировки (10) в большом канонич. распределении определяюттермодинамич. потенциал
представляющим собой объединённую запись 1-го и 2-го начала термодинамики(см. Второе начало термодинамики )для обратимых процессов, находим, что величина Т в ф-ле (7) равна абс. темп-ре тела, а производная dF/дТ - взятой с обратным знаком энтропии S. Следовательно,F - свободная энергия тела, что и выявляет её статистич. смысл. Аналогично условию нормировки (10) в большом канонич. распределении определяюттермодинамич. потенциал 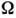 ,связанный со свободной энергией соотношением:
,связанный со свободной энергией соотношением: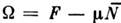 .
.Особое значение имеет статистич. истолкование энтропии, к-рое следуетиз ф-лы (8). Формально суммирование в этой ф-ле производится по всем состояниямс энергией Е п, но фактически существенно лишь относительнонебольшое их число с энергией вблизи ср. энергии. Число
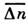 этих существ. состояний поэтому естественно определить, ограничив суммированиев ф-ле (8) интервалом
этих существ. состояний поэтому естественно определить, ограничив суммированиев ф-ле (8) интервалом 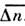 ,заменив Е п на ср. энергию
,заменив Е п на ср. энергию 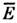 и вынося экспоненту из-под знака суммы. Тогда сумма даст
и вынося экспоненту из-под знака суммы. Тогда сумма даст 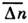 иф-ла (8) примет вид:
иф-ла (8) примет вид: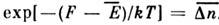 .
.С др. стороны, согласно термодинамике, F = E - TS, чтодаёт связь энтропии с числом микроскопич. состояний, иначе говоря, со статистическимвесом макроскопич. состояния, пропорциональным его вероятности:

При темп-ре абс. нуля любая система находится в определённом (основном)состоянии, так что
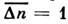 , S = 0. Это утверждение выражает собой третье начало термодинамики. Здесь существенно, что для однозначного определения энтропии нужнопользоваться именно квантовой ф-лой (9); в чисто классической С. ф. энтропияопределена только с точностью до произвольного слагаемого.
, S = 0. Это утверждение выражает собой третье начало термодинамики. Здесь существенно, что для однозначного определения энтропии нужнопользоваться именно квантовой ф-лой (9); в чисто классической С. ф. энтропияопределена только с точностью до произвольного слагаемого.Смысл энтропии как меры вероятности состояния сохраняется и для неравновесныхсостояний. В этом случае ф-лу (11) следует рассматривать как общее определениеэнтропии состояния. Ясно, что в природе «самопроизвольно» (т. е. в замкнутойсистеме) могут идти лишь процессы, приводящие к увеличению вероятностисостояния. Обратные процессы являются крайне маловероятными. [Энтропиясистемы пропорциональна числу частиц в ней, поэтому статистич. веса двухфизически достаточно близких состояний, будучи пропорциональны ехр(-S/k), различаются очень сильно.] Это даёт статистич. обоснование закону возрастанияэнтропии, согласно к-рому энтропия замкнутой системы может только увеличиваться. В состоянии равновесия энтропия имеет максимально возможное в данных внеш. условиях значение. Следовательно, равновесное состояние является состояниемс макс. статистич. весом, т. е. наиб. вероятным состоянием.
Из определения (11) следует, что энтропия аддитивна, т. е. энтропиятела, состоящего из слабовзаимодействующих частей, равна сумме энтропииэтих частей. Это даёт возможность вычислить энтропию в важном случае, когдатело состоит из частей, к-рые находятся в равновесии сами по себе, но недруг с другом. Отметим, что ф-лы С. ф., будучи справедливы для систем избольшого числа частиц, подразумевают переход к термодинамическому пределу, когда число частиц в теле N и объём V стремятся к бесконечности, а плотность N/V остаётся конечной. Именно в этом пределе термодинамич. потенциалы, определяемые распределением Гиббса, оказываются пропорциональнымиобъёму.
Несмотря на ясность физ. основ С. ф., стремление дать ей строгое матем. обоснование поставило ряд важных и трудных матем. проблем. Напр., обоснованиераспределения (4) требует доказательства зргодической гипотезы. Методическиинтересен вопрос об устойчивости осн. состояния системы из большого числачастиц (электронов и ядер), взаимодействующих по закону Кулона. Процессырелаксации неравновесных состояний связаны с неустойчивостью фазовых траекториймеханич. систем, состоящей в том, что проходящие через две близкие точкифазового пространства траектории экспоненциально расходятся по мере удаленияот этих точек.
Внешние поля. Ф-ла (8), связывающая свободную энергию F со статистич. суммой, является основой для вычисления термодинамич. величин методамиС. ф. Эту ф-лу используют, в частности, для построения статистич. теорииэлектрич. и магн. свойств вещества. Напр., для вычисления магн. моментатела в магн. поле Н следует вычислить статистич. сумму и свободнуюэнергию. Магн. момент М тела выражается тогда ф-лой: М= -дР/дН.
При наличии слабого гравитац. поля требование максимальности энтропииприводит к след. условию равновесия:
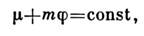
где
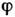 - гравитац. потенциал, m - масса частицы. Это ур-ние описывает, напр.,изменение плотности тела под действием гравитац. сил. Интересные явлениядолжны наблюдаться в сильных гравитац. полях, когда существенны релятивистскиеэффекты. В таких полях, согласно общей теории относительности, в состоянииравновесия от координат зависит не только плотность, но и темп-pa тела. Известное изменение представлений С. ф. требуется, по-видимому, для последоват. описания чёрных дыр - тел, гравитац. поле к-рых настолько сильно, что световые лучи не могут выйти из их внутр. областей в окружающее пространство. Чёрная дыра испускает излучение, темп-pa к-рого однозначно связана с еёрадиусом. Суммарная площадь поверхности чёрных дыр может подобно энтропиитолько увеличиваться, чем устанавливается глубокая, но не вполне яснаясвязь теории тяготения с законом возрастания энтропии.
- гравитац. потенциал, m - масса частицы. Это ур-ние описывает, напр.,изменение плотности тела под действием гравитац. сил. Интересные явлениядолжны наблюдаться в сильных гравитац. полях, когда существенны релятивистскиеэффекты. В таких полях, согласно общей теории относительности, в состоянииравновесия от координат зависит не только плотность, но и темп-pa тела. Известное изменение представлений С. ф. требуется, по-видимому, для последоват. описания чёрных дыр - тел, гравитац. поле к-рых настолько сильно, что световые лучи не могут выйти из их внутр. областей в окружающее пространство. Чёрная дыра испускает излучение, темп-pa к-рого однозначно связана с еёрадиусом. Суммарная площадь поверхности чёрных дыр может подобно энтропиитолько увеличиваться, чем устанавливается глубокая, но не вполне яснаясвязь теории тяготения с законом возрастания энтропии.Иерархия функций распределения. Кроме N-частичной ф-ции распределения w, определяемой ф-лой (1), можно ввести ф-ции более низкого порядка, получающиеся из wинтегрированием по части переменных. Так, интегрируяпо координатам и импульсам всех частиц, кроме одной, получаем одночастичнуюф-цию w(1) (r,p,t), по переменным всех частиц, кроме двух, - двухчастичную ф-цию w(2) (r1,р 1,r2,р 2,t )и т. д. В состоянии равновесия, согласно ф-ле (5), зависимость w отимпульсов очевидна и достаточно рассматривать лишь координатные зависимости, т. е. ф-цию f(1)(r), к-рая сводится для однородного телав отсутствие внеш. поля к постоянной, f(2)(r1,r2),f(3)(r1,r2,r3) и т. д. Все эти ф-ции стремятся при больших значениях аргументов к постоянным, к-рые можно выбрать равными 1. Существует «цепочка ур-ний», связывающихф-ции порядка l и l+ 1 (см. Боголюбова уравнения). Напр.,для частиц, взаимодействие к-рых описывается парной потенциальной энергией u(r), дифференцируя ф-лу (5) по r2 и интегрируя по всемпеременным, кроме r1 и r2, получаемур-ние
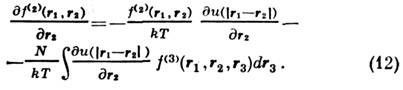
Если на основании дополнит. соображений, связанных со спецификой конкретнойпроблемы, выразить f(3) через f(2),последнюю можно определить из (12). Статистич. сумма Z после этогоопределяется через f(2) простым интегрированием. В неравновесномслучае аналогичные соотношения, содержащие производные по времени, можнополучить для ф-ций w(1), w(2) и т. д. Флуктуации. В основе С. ф. лежит тот факт, что физ. величины, характеризующие макроскопич. тела, с большой точностью равны своим ср. значениям. Это равенство являетсявсё же приближённым, в действительности все величины испытывают малые беспорядочныеотклонения от ср. значений - флуктуации. Существование флуктуацииимеет принципиальное значение, т. к. доказывает статистич. характер термодинамич. закономерностей. Кроме того, флуктуации играют роль шума, ограничивающеготочность физ. измерений. Флуктуации нек-рой величины х около еёср. значения
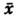 характеризуются ср. квадратом флуктуации
характеризуются ср. квадратом флуктуации 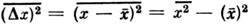 . В подавляющембольшинстве случаев величина х испытывает флуктуации порядка
. В подавляющембольшинстве случаев величина х испытывает флуктуации порядка 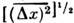 ; существенно большие флуктуации встречаются крайне редко. Знание ф-циираспределения системы позволяет вычислить ср. квадрат флуктуации точнотак же, как и ср. значение любой физ. величины. Малые флуктуации термодинамич. величин можно вычислить, используя статистич. истолкование энтропии. Согласноф-ле (11), вероятность неравновесного состояния системы с энтропией . пропорциональна exp(S/k). Это приводит к равенству
; существенно большие флуктуации встречаются крайне редко. Знание ф-циираспределения системы позволяет вычислить ср. квадрат флуктуации точнотак же, как и ср. значение любой физ. величины. Малые флуктуации термодинамич. величин можно вычислить, используя статистич. истолкование энтропии. Согласноф-ле (11), вероятность неравновесного состояния системы с энтропией . пропорциональна exp(S/k). Это приводит к равенству 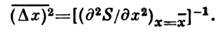
Напр., для ср. квадратов флуктуации объёма и темп-ры тела получим:
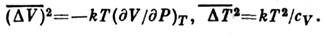
Из этих ф-л видно, что относит. флуктуации объёма и флуктуации темп-рыобратно пропорциональны N1/2, где N - число частиц в теле. Этои обеспечивает малость флуктуации для макроскопич. тел. Связь между флуктуациямиразл. величин xi, х k характеризуется ф-цией
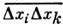 . Если флуктуации величин х i и xk статистическинезависимы, то
. Если флуктуации величин х i и xk статистическинезависимы, то 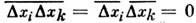
Под xi и х k можно понимать и значенияодной и той же величины, напр. плотности, в разл. точках пространства. Т. о., приходим к пространственной корреляционной функции плотности:
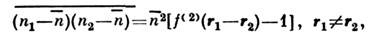
где n1 и n2 - значения плотностичисла частиц в точках r1 и r2, га -ср. значение плотности, f(2) - введённая выше двухчастичнаяф-ция распределения. С увеличением расстояния между точками корреляц. ф-циястремится к нулю (обычно экспоненциально), т. к. флуктуации в далёких точкахпространства происходят независимо. Расстояние, на к-ром эта ф-ция существенноубывает, наз. корреляц. радиусом.
Закон равнораспределения. Приложения С. ф. к изучению свойствконкретных систем сводятся к приближённому вычислению статистич. суммыс учётом специфич. свойств системы. Во мн. случаях эта задача упрощаетсяприменением закона равнораспределения по степеням свободы, утверждающего, что теплоёмкость су (при пост. объёме V )системы взаимодействующихчастиц, совершающих гармонич. колебания, равна:
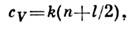
где l - общее число поступат. и вращат. степеней свободы, п- число колебат. степеней свободы. Доказательство закона основано натом, что ф-ция Гамильтона H такой системы имеет вид: Н = К(р 1)+ и(х т), где кинетич. энергия К - однороднаяквадратичная ф-ция от l + n импульсов pi, а потенциальнаяэнергия и - квадратичная ф-ция от п колебат. координат х т. В статистич. интеграле (6) интегрирование по колебат. координатам ввидубыстрой сходимости интеграла можно распространить от
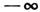 до
до 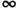 . Послеэтого легко показать, что внутр. энергия линейно зависит от темп-ры, откудаследует приведённое выражение для теплоёмкости. Отметим, что закон равнораспределенияверен только в классической С. ф.
. Послеэтого легко показать, что внутр. энергия линейно зависит от темп-ры, откудаследует приведённое выражение для теплоёмкости. Отметим, что закон равнораспределенияверен только в классической С. ф.Идеальный газ. Простейшим объектом исследования в С. ф. являетсяидеальный газ, т. е. газ настолько разреженный, что можно пренебречь взаимодействиеммежду его молекулами. Энергия такого газа равна просто сумме энергий отд. молекул. В классической С. ф. это означает, что ф-ция распределения распадаетсяна произведение ф-ций распределения для отд. молекул. В дальнейшем дляпростоты рассматривается одноатомный газ. Энергия атома во внеш. поле спотенциальной энергией u(r) равна
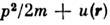 . Интегрируя ф-лу (5) по координатам xi и импульсам pi всех атомов, кроме одного, находим число атомов, импульсы к-рых лежат вэлементе объёма импульсного пространства dp, а координаты - в элементеобъёма dx:
. Интегрируя ф-лу (5) по координатам xi и импульсам pi всех атомов, кроме одного, находим число атомов, импульсы к-рых лежат вэлементе объёма импульсного пространства dp, а координаты - в элементеобъёма dx: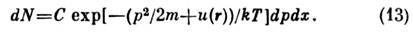
Эту ф-лу называют распределением Максвелла - Больцмана (см. Вольцманастатистика). Статистич. интеграл (9) идеального классич. газа такжераспадается на произведение членов, соответствующих отд. атомам. При этом, однако, нужно учесть, что осн. состояние атома может быть вырождено, т. е. g состояний могут иметь одинаковую энергию. Это приведёт к появлениюдополнит. множителя gN в статистич. сумме. Окончательносвободная энергия N атомов газа равна:
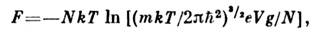
здесь V - объём газа, е - основание натуральных логарифмов. При высоких темп-pax g = (2J + 1)(2L + 1), где J- величина спина,a L- орбитального момента атома (в единицах
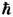 ).Из выражения для свободной энергии следует, что зависимость давления . идеального газа от плотности числа частиц (N/V )и темп-ры имеетвид: PV = NkT. Для внутр. энергии одноатомного газа, его теплоёмкостипри пост. объёме и хим. потенциала получим:
).Из выражения для свободной энергии следует, что зависимость давления . идеального газа от плотности числа частиц (N/V )и темп-ры имеетвид: PV = NkT. Для внутр. энергии одноатомного газа, его теплоёмкостипри пост. объёме и хим. потенциала получим: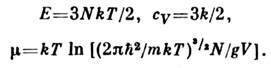
Характерно, что даже для невырожденного (т. е. с достаточной точностьюподчиняющегося классич. механике) газа выражения для свободной энергиии хим. потенциала содержат постоянную Планка
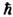 .Это обусловлено отмеченной ранее связью энтропии с понятием числа квантовыхсостояний.
.Это обусловлено отмеченной ранее связью энтропии с понятием числа квантовыхсостояний.В случае двухатомных и многоатомных газов вклад в термодинамич. ф-циивносят также колебания и вращение молекул.
Неидеальный газ. Важное достижение С. ф.- вычисление поправокк термодинамич. величинам газа, связанных с взаимодействием между его частицами. С этой точки зрения уравнение состояния идеального газа являетсяпервым членом разложения давления реального газа по степеням плотностичисла частиц, поскольку всякий газ при достаточно малой плотности ведётсебя как идеальный. С повышением плотности начинают играть роль поправкик ур-нию состояния, связанные с взаимодействием, так что давление описывается вириальным разложением:
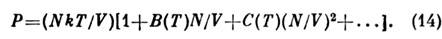
Для нахождения второго в и р и а л ь н о г о коэффициента В(Т )одноатомногогаза достаточно считать, что в газе одноврем. взаимодействуют только дваатома. Задача сводится в таком случае к вычислению статистич. суммы двухатомов с энергией взаимодействия u(r), в результате
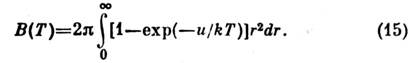
По порядку величины В равен
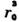 ,где r0 - характерный размер атома, или, точнее, радиусдействия межатомных сил. Это означает, что ряд (14) фактически представляетсобой разложение по степеням безразмерного газового параметра
,где r0 - характерный размер атома, или, точнее, радиусдействия межатомных сил. Это означает, что ряд (14) фактически представляетсобой разложение по степеням безразмерного газового параметра Плазма. Особый случай неидеального
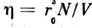 газапредставляет собой плазма - частично или полностью ионизов. газ, в к-ромимеются свободные электроны и ионы. При вычислении поправок к термодинамич. ф-циям плазмы существенно, что электроны и ионы взаимодействуют электростатически(по закону Кулона). Кулоновские силы медленно убывают с расстоянием, поэтомуинтеграл во втором вириальном коэф. ф-лы (15) расходится на больших расстояниях r между частицами. В действительности под влиянием кулоновских силраспределение ионов и электронов в плазме изменяется т. о., что поле каждойчастицы экранируется, т. е. быстро убывает на расстоянии, называемом дебаевскимрадиусом экранирования и равном по порядку величины
газапредставляет собой плазма - частично или полностью ионизов. газ, в к-ромимеются свободные электроны и ионы. При вычислении поправок к термодинамич. ф-циям плазмы существенно, что электроны и ионы взаимодействуют электростатически(по закону Кулона). Кулоновские силы медленно убывают с расстоянием, поэтомуинтеграл во втором вириальном коэф. ф-лы (15) расходится на больших расстояниях r между частицами. В действительности под влиянием кулоновских силраспределение ионов и электронов в плазме изменяется т. о., что поле каждойчастицы экранируется, т. е. быстро убывает на расстоянии, называемом дебаевскимрадиусом экранирования и равном по порядку величины 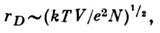 где N - число электронов, е - заряд электрона. Все частицы, находящиеся внутри сферы дебаевского радиуса, одноврем. принимают участиево взаимодействии, поэтому первая поправка к давлению пропорциональна не(N/V)2, как в обычном газе, а более низкой степени плотности(N/V)3/2. Количеств. расчёт основан на том, что частицыраспределены в поле выбранного электрона (или иона) согласно распределениюБольцмана. В результате ур-ние состояния имеет вид:
где N - число электронов, е - заряд электрона. Все частицы, находящиеся внутри сферы дебаевского радиуса, одноврем. принимают участиево взаимодействии, поэтому первая поправка к давлению пропорциональна не(N/V)2, как в обычном газе, а более низкой степени плотности(N/V)3/2. Количеств. расчёт основан на том, что частицыраспределены в поле выбранного электрона (или иона) согласно распределениюБольцмана. В результате ур-ние состояния имеет вид: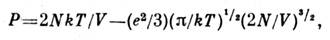
если в плазме имеются только однозарядные ионы. Такого же рода поправкивозникают и в термодинамич. ф-циях электролитов, в к-рых имеются свободныеионы растворённых веществ.
Жидкости. В отличие от газа, для жидкости связанные с взаимодействиемчлены в ур-нии состояния не малы. Поэтому свойства жидкости сильно зависятот конкретного характера взаимодействия между её молекулами. В теории жидкостивообще отсутствует малый параметр, к-рый можно было бы использовать дляупрощения теории. Невозможно получить к.-л. аналитич. ф-лы для термодинамич. величин жидкости. Одним из способов преодоления этой трудности являетсяизучение системы, состоящей из сравнительно небольшого числа частиц (~неск. тысяч). В этом случае, используя ЭВМ, можно провести прямое решение ур-нийдвижения частиц и определить таким способом ср. значения всех характеризующихсистему величин без дополнит, предположений (см. Молекулярной динамикиметод). Удаётся исследовать и процесс приближения такой системы к состояниюравновесия. Можно также найти статистич. интеграл для такой системы изнебольшого числа частиц, вычисляя на ЭВМ соответствующие интегралы (обычнопри этом используют Монте-Карло метод). Полученные этими способамирезультаты имеют, однако, малую точность в приложении к реальным жидкостямиз-за малого числа частиц в системе.
Ещё один способ построения теории жидкости основан на использованииур-ния (12), связывающего двух- и трёхчастичные ф-ции распределения. Втеории жидкости это точное соотношение дополняют нек-рыми приближённымиф-лами, выражающими трёхчастичную ф-цию через двухчастичную. В результатеполучается ур-ние для двухчастичной ф-ции, к-рое решают численно. Дополнит. соотношения находят на основании правдоподобных физ. соображений, они носятинтерполяц. характер, так что основанные на них теории могут претендоватьлишь на ограниченную точность. Тем не менее даже такое описание имеет важноезначение, поскольку в нём проявляется общность законов С. ф. (см. также Жидкость, Гиперцепное уравнение, Перкуса - Йевика уравнение).
Вырожденные газы. Если понижать темп-ру газа при пост. плотности, начинают проявляться квантовомеханич. эффекты, связанные со свойствамисимметрии волновых ф-ций системы тождественных частиц, т. е. газ вырождается. Это вырождение наступает при темн-рах, когда длина волны де Бройля длячастиц, движущихся с тепловой скоростью, становится порядка ср. расстояниямежду ними (см. Квантовый газ).
Для частиц с полуцелым спином волновая ф-ция должна менять знак приперестановке любой пары частиц, поэтому в одном квантовом состоянии неможет находиться больше одной частицы (Паули принцип). Кол-во частицс целым спином в одном состоянии может быть любым, но требуемая в этомслучае неизменность волновой ф-ции при перестановке частиц и здесь приводитк изменению статистич. свойств газа. Частицы с полуцелым спином описываются Ферми - Дирака статистикой, их называют фермионами. К фермионамотносятся, напр., электроны, протоны, нейтроны, атомы дейтерия, атомы 3 Не. Частицы с целым спином (бозоны) описываются Бозе - Эйнштейна статистикой. К ним относятся, напр., атомы Н, 4 Не, кванты света - фотоны.
Пусть ср. число частиц газа в единице объёма с импульсами, лежащимив интервале dp, есть
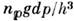 , так что п р - число частиц в одной ячейке фазового пространства. Тогда из распределения Гиббса следует, что для идеальных газов фермионов(верхний знак) и бозонов (нижний знак)
, так что п р - число частиц в одной ячейке фазового пространства. Тогда из распределения Гиббса следует, что для идеальных газов фермионов(верхний знак) и бозонов (нижний знак)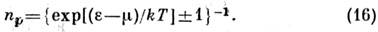
В этой ф-ле
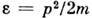 - энергия частицы с импульсом р,
- энергия частицы с импульсом р,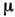 - хим. потенциал, определяемый из условия постоянства числа частиц N в системе:
- хим. потенциал, определяемый из условия постоянства числа частиц N в системе: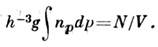
Ф-ла (16) переходит в ф-лу распределения Больцмана (13) при
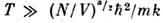 ; величина справа наз. темп-рой вырождения.
; величина справа наз. темп-рой вырождения.В случае фермионов, как и должно быть,
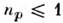 , поэтому частицы ферми-газа и при Т- 0 обладают отличными от нуляимпульсами, поскольку в состоянии с нулевым импульсом может находитьсятолько одна частица. Точнее, при Т =0 для ферми-газа п р=1 внутри фермы-поверхности - сферы в импульсном пространствес радиусом
, поэтому частицы ферми-газа и при Т- 0 обладают отличными от нуляимпульсами, поскольку в состоянии с нулевым импульсом может находитьсятолько одна частица. Точнее, при Т =0 для ферми-газа п р=1 внутри фермы-поверхности - сферы в импульсном пространствес радиусом 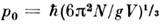 ;вне этой сферы n р = 0. При конечных, но низких темп-pax п р меняется от 1 внутри сферы до нуля вне сферы постепенно, причём ширина переходной области ~ mkT/p0. Величина п р для ферми-газа как ф-ция от энергии e изображена схематически на рис.1 . При изменении темп-ры газа меняется состояние частиц только в этомпереходном слое, поэтому теплоёмкость ферми-газа при низких темп-pax пропорциональна Т и равна:
;вне этой сферы n р = 0. При конечных, но низких темп-pax п р меняется от 1 внутри сферы до нуля вне сферы постепенно, причём ширина переходной области ~ mkT/p0. Величина п р для ферми-газа как ф-ция от энергии e изображена схематически на рис.1 . При изменении темп-ры газа меняется состояние частиц только в этомпереходном слое, поэтому теплоёмкость ферми-газа при низких темп-pax пропорциональна Т и равна: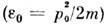
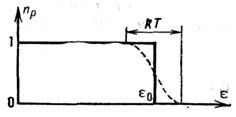
Рис. 1. Функция распределения Ферми - Дирака.
В
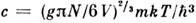 бозе-газе при Т =0 все частицы находятся в состоянии с нулевымимпульсом. При достаточно низких темп-pax в состоянии с р = 0 находитсяконечная доля всех частиц; эти частицы образуют т. н. бозе-эйнштейновскийконденсат. Остальные частицы находятся в состояниях с р
бозе-газе при Т =0 все частицы находятся в состоянии с нулевымимпульсом. При достаточно низких темп-pax в состоянии с р = 0 находитсяконечная доля всех частиц; эти частицы образуют т. н. бозе-эйнштейновскийконденсат. Остальные частицы находятся в состояниях с р 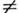 0, причём их число определяется
0, причём их число определяется ф-лой (16) с
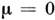 . При темп-ре
. При темп-ре 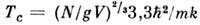
в бозе-газе происходит фазовый переход. Доля частиц с нулевымимпульсом обращается в нуль, Бозе - Эйнштейна конденсация исчезает. Схематически ф-ции распределения Максвелла, Ферми - Дирака и Бозе - Эйнштейна(при Т Т с )изображены на рис. 2.
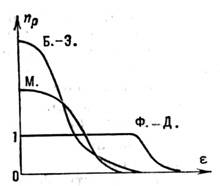
Рис. 2. Сравнение функций распределения Максвелла (М.), Ферми - Дирака(Ф.- Д.) и Бозе - Эйнштейна (Б.- Э.).
Особым случаем применения статистики Бозе - Эйнштейна является равновесноеэл.-магн. излучение, к-рое можно рассматривать как газ, состоящий из фотонов. Энергия фотона связана с его импульсом соотношением
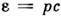 , где с- скорость света в вакууме. Число фотонов не является заданнойвеличиной, а само определяется из условия термодинамич. равновесия, поэтомуих распределение по импульсам даётся ф-лой (16) с
, где с- скорость света в вакууме. Число фотонов не является заданнойвеличиной, а само определяется из условия термодинамич. равновесия, поэтомуих распределение по импульсам даётся ф-лой (16) с 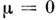 (причём
(причём 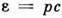 ).Т. о. получается ф-ла Планка для спектра равновесного (чёрного) излучения(см. Планка закон излучения).
).Т. о. получается ф-ла Планка для спектра равновесного (чёрного) излучения(см. Планка закон излучения).Квазичастицы. Вблизи абс. нуля темп-р гл. вклад в статистич. сумму вносят слабовозбуждённые квантовые состояния, близкие по энергиик основному. Вычисление энергии осн. состояния является чисто квантовомеханич. задачей, предметом квантовой теории многих частиц. Тепловое движениев таких условиях можно описать как появление в системе слабовзаимодействующих квазичастиц (элементарных возбуждений), обладающих энергией
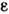 и импульсом (в кристаллах - квазиимпульсом) р. Зная зависимость
и импульсом (в кристаллах - квазиимпульсом) р. Зная зависимость 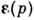 , можно вычислить зависящую от темп-ры часть термодинамич. ф-ций по ф-ламдля идеального ферми-или бозе-газа в зависимости от статистики квазичастиц. Особенно важно, что бозевские квазичастицы с малыми р можно рассматриватькак кванты длинноволновых колебаний, описываемых макроскопич. ур-ниями. Так, в кристаллах (и бозе-жидкостях) существуют фононы (кванты звука),в магнетиках - магноны (кванты колебаний магн. момента).
, можно вычислить зависящую от темп-ры часть термодинамич. ф-ций по ф-ламдля идеального ферми-или бозе-газа в зависимости от статистики квазичастиц. Особенно важно, что бозевские квазичастицы с малыми р можно рассматриватькак кванты длинноволновых колебаний, описываемых макроскопич. ур-ниями. Так, в кристаллах (и бозе-жидкостях) существуют фононы (кванты звука),в магнетиках - магноны (кванты колебаний магн. момента).Особые типы квазичастиц существуют в двумерных и одномерных системах. В плоской кристаллич. плёнке их роль играют дислокации, в плёнках Не -вихревые нити, в полимерных нитях-солитоны и доменные стенки. В трёхмерныхтелах эти объекты имеют большую энергию и не вносят вклада в термодинамич. ф-ции.
Неидеальные вырожденные газы. Исследование свойств таких газовпри условии малости газового параметра
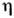 представляет существ. интерес. В фермиевском газе поправка к энергии осн. состояния оказывается
представляет существ. интерес. В фермиевском газе поправка к энергии осн. состояния оказывается 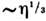 . Спектр квазичастиц в случае газа с отталкиванием между частицами совпадает(с точностью до поправок
. Спектр квазичастиц в случае газа с отталкиванием между частицами совпадает(с точностью до поправок 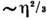 )со спектром свободных частиц. В спектре газа с притяжением между частицамивозникает экспоненциально малая (по параметру
)со спектром свободных частиц. В спектре газа с притяжением между частицамивозникает экспоненциально малая (по параметру 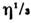 )щель, что связано со сверхтекучестью (см. также Сверхпроводимость), и появляется фононная ветвь. Энергия осн. состояния, равная нулю уидеального бозе-газа, составляет
)щель, что связано со сверхтекучестью (см. также Сверхпроводимость), и появляется фононная ветвь. Энергия осн. состояния, равная нулю уидеального бозе-газа, составляет 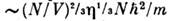 для неидеального. Спектр квазичастиц при малых р является фононным, а при больших р переходит в спектр свободных частиц (см. также Квантоваяжидкость).
для неидеального. Спектр квазичастиц при малых р является фононным, а при больших р переходит в спектр свободных частиц (см. также Квантоваяжидкость).Кристаллическая решётка. Атомы в решётке совершают малые колебанияоколо своих положений равновесия. Это означает, что их тепловое движениеможно рассматривать как совокупность квазичастиц (фононов) при всех (ане только низких) темп-pax (см. Колебания кристаллической решётки). Распределение фононов, как и фотонов, даётся ф-лой (16) с
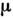 = 0. При низких темп-pax существенны лишь длинноволновые фононы, к-рыепредставляют собой кванты звуковых волн, описываемых ур-ниями теории упругости. Зависимость
= 0. При низких темп-pax существенны лишь длинноволновые фононы, к-рыепредставляют собой кванты звуковых волн, описываемых ур-ниями теории упругости. Зависимость 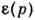 для них линейна, поэтому теплоёмкость кристаллич. решётки пропорциональна Т 3. При высоких темп-pax можно пользоваться законом равнораспределенияэнергии по степеням свободы, так что теплоёмкость не зависит от темп-рыи равна 3Nk, где N - число атомов в кристалле. Зависимость
для них линейна, поэтому теплоёмкость кристаллич. решётки пропорциональна Т 3. При высоких темп-pax можно пользоваться законом равнораспределенияэнергии по степеням свободы, так что теплоёмкость не зависит от темп-рыи равна 3Nk, где N - число атомов в кристалле. Зависимость 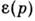 при произвольных р можно определить из опытов по неупругому рассеяниюнейтронов в кристалле или вычислить теоретически, задавая значения «силовыхконстант», определяющих взаимодействие атомов в решётках. Новые проблемывстали перед С. ф. в связи с открытием т. н. квазипериодич. кристаллов, молекулы к-рых расположены в пространстве непериодически, но в нек-ромпорядке (см. Квазикристалл).
при произвольных р можно определить из опытов по неупругому рассеяниюнейтронов в кристалле или вычислить теоретически, задавая значения «силовыхконстант», определяющих взаимодействие атомов в решётках. Новые проблемывстали перед С. ф. в связи с открытием т. н. квазипериодич. кристаллов, молекулы к-рых расположены в пространстве непериодически, но в нек-ромпорядке (см. Квазикристалл).Металлы. В металлах вклад в термодинамич. ф-ции дают также электроныпроводимости. Состояние электрона в металле характеризуется квазиимпульсом, и т. к. электроны подчиняются статистике Ферми - Дирака, их распределениепо квазиимпульсам даётся ф-лой (16). Поэтому теплоёмкость электронногогаза, а следовательно, и всего металла при достаточно низких темп-pax пропорциональна Т. Отличие от ферми-газа свободных частиц состоит в том, что ферми-поверхностьуже не является сферой, а представляет собой нек-рую сложную поверхностьв пространстве квазиимпульсов. Форму поверхности Ферми, равно как и зависимостьэнергии от квазиимпульса вблизи этой поверхности, можно определять экспериментально, гл. обр. исследуя магн. свойства металлов, а также рассчитывать теоретически, используя т. н. модель псевдопотенциала. В сверхпроводниках возбуждённыесостояния электрона отделены от ферми-поверхности щелью, что приводит кэкспоненц. зависимости электронной теплоёмкости от темп-ры. В ферромагн. и антиферромагн. веществах вклад в термодинамич. ф-ции дают также колебаниямагн. моментов (спиновые волны).
В диэлектриках и полупроводниках при Т= 0 свободные электроныотсутствуют. При конечных темп-рах в них появляются заряж. квазичастицы:электроны с отрицат. зарядом и «дырки» с положит. зарядом. Электрон и дыркамогут образовать связанное состояние - квазичастицу, называемую экситоном. Др. тип экситона представляет собой возбуждённое состояние атома диэлектрика, перемещающееся в кристаллич. решётке.
Методы квантовой теории поля в статистической физике. При решениизадач квантовой С. ф., прежде всего при исследовании свойств квантовыхжидкостей, электронов в металлах и магнетиках, важное значение имеют методыквантовой теории поля, введённые в С. ф. сравнительно недавно. Осн. рольв этих методах играет Грина функция макроскопич. системы, аналогичнаяф-ции Грина в квантовой теории поля. Она зависит от энергии е и импульса р, закон дисперсии квазичастиц e(р) определяется из ур-ния
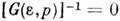 , т. к. энергия квазичастицы является полюсом ф-ции Грина. Существует регулярныйметод вычисления ф-ций Грина в виде ряда по степеням энергии взаимодействиямежду частицами. Каждый член этого ряда содержит многократные интегралыпо энергиям и импульсам от ф-ций Грина невзаимодействующих частиц и можетбыть изображён графически в виде диаграмм, аналогичных Фейнмана диаграммам в квантовой электродинамике. Каждая из этих диаграмм имеет определ. физ. смысл, что позволяет отделить в бесконечном ряду члены, ответственныеза интересующее явление, и просуммировать их. Существует также диаграммнаятехника для вычисления температурных ф-ций Грина, позволяющих находитьтермодинамич. величины непосредственно, без введения квазичастиц. В этойтехнике гриновские ф-ции зависят (вместо энергии) от нек-рых дискретныхчастот wn и интегралы по энергиям заменяются на сумму по этимчастотам.
, т. к. энергия квазичастицы является полюсом ф-ции Грина. Существует регулярныйметод вычисления ф-ций Грина в виде ряда по степеням энергии взаимодействиямежду частицами. Каждый член этого ряда содержит многократные интегралыпо энергиям и импульсам от ф-ций Грина невзаимодействующих частиц и можетбыть изображён графически в виде диаграмм, аналогичных Фейнмана диаграммам в квантовой электродинамике. Каждая из этих диаграмм имеет определ. физ. смысл, что позволяет отделить в бесконечном ряду члены, ответственныеза интересующее явление, и просуммировать их. Существует также диаграммнаятехника для вычисления температурных ф-ций Грина, позволяющих находитьтермодинамич. величины непосредственно, без введения квазичастиц. В этойтехнике гриновские ф-ции зависят (вместо энергии) от нек-рых дискретныхчастот wn и интегралы по энергиям заменяются на сумму по этимчастотам.Фазовые переходы. При непрерывном изменении внеш. параметров (напр.,давления или темп-ры) свойства системы могут при нек-рых значениях параметровизмениться скачкообразно, т. е. происходит фазовый переход. Фазовые переходыделятся на переходы 1-го рода, сопровождающиеся выделением скрытой теплотыперехода и скачкообразным изменением объёма (напр., плавление), и переходы2-го рода, в к-рых скрытая теплота и скачок объёма отсутствуют, а имеетсяскачок теплоёмкости (напр., переход в сверхпроводящее состояние). При переходе2-го рода меняется симметрия тела. Это изменение количественно характеризуется параметром порядка, отличным от нуля в одной из фаз и обращающимсяв нуль в точке перехода. Статистич. теория фазовых переходов составляетважную, но ещё далёкую от завершения область С. ф. наиб. трудность длятеоретич. исследования представляют при этом свойства вещества вблизи критическойточки, фазового перехода 1-го рода и в непосредств. близости линиифазового перехода 2-го рода. (На нек-ром расстоянии от этой линии переход2-го рода описывается Ландау теорией. )Здесь аномально возрастаютфлуктуации, и рассмотренные выше приближённые методы С. ф. неприменимы. Поэтому важную роль играют точно решаемые модели, в к-рых есть переходы(см. Двумерные решёточные модели). Существ. продвижение в построениифлуктуац. теории фазовых переходов достигнуто методом эпсилон-разложения. В нём переход исследуется в воображаемом пространстве с числом измерений
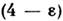 , а результаты экстраполируются к
, а результаты экстраполируются к 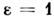 ,т. е. реальному пространству трёх измерений. В двумерных системах возможнысвоеобразные фазовые переходы, когда при нек-рой темп-ре появляются дислокацииили вихревые нити. Параметр порядка в точке перехода обращается в нульскачком, а теплоёмкость непрерывна.
,т. е. реальному пространству трёх измерений. В двумерных системах возможнысвоеобразные фазовые переходы, когда при нек-рой темп-ре появляются дислокацииили вихревые нити. Параметр порядка в точке перехода обращается в нульскачком, а теплоёмкость непрерывна.Неупорядоченные системы. Своеобразное место в С. ф. занимают стёкла- твёрдые тела, атомы к-рых расположены беспорядочно даже при абс. нуле темп-р. Строго говоря, такое состояние является неравновесным, нос чрезвычайно большим временем релаксации, так что неравновесность фактическине проявляется. Теплоёмкость стёкол при низких темп-pax линейно зависитот Т. Это следует из выражения для Z в виде (8). При
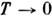 зависимость от Т определяется поведением g(E )при малых Е. Но для неупорядоченных систем значение Е =0 ничем невыделено, так что g(0 )конечно, Z = А+ е(0)Т и с~ Т. Интересной особенностью стёкол является зависимость наблюдаемыхзначений теплоёмкости от времени измерения. Это объясняется тем, что уровниэнергии с малыми Е связаны с квантовым туннелированием атомов черезвысокий потенциальный барьер, требующим большого времени. Интересны свойства спиновых стёкол - систем беспорядочно расположенных атомов, имеющихмагн. моменты.
зависимость от Т определяется поведением g(E )при малых Е. Но для неупорядоченных систем значение Е =0 ничем невыделено, так что g(0 )конечно, Z = А+ е(0)Т и с~ Т. Интересной особенностью стёкол является зависимость наблюдаемыхзначений теплоёмкости от времени измерения. Это объясняется тем, что уровниэнергии с малыми Е связаны с квантовым туннелированием атомов черезвысокий потенциальный барьер, требующим большого времени. Интересны свойства спиновых стёкол - систем беспорядочно расположенных атомов, имеющихмагн. моменты.Статистическая физика неравновесных процессов. Всё большее значениеприобретает кинетика физическая - раздел С. ф., в к-ром изучаютпроцессы в системах, находящихся в неравновесных состояниях. Здесь возможныдве постановки вопроса: можно рассматривать систему в нек-ром неравновесномсостоянии и следить за её переходом в состояние равновесия; можно рассматриватьсистему, неравновесное состояние к-рой поддерживается внеш. условиями, напр. тело, в к-ром задан градиент темп-ры, протекает электрич. ток и т. п., или тело, находящееся в перем. внеш. поле.
Если отклонение от равновесия мало, неравновесные свойства системы описываютсят. н. кинетическими коэффициентами. Примерами таких коэф. являютсякоэф. вязкости, теплопроводности и диффузии, электропроводность металлови т. п. Эти величины удовлетворяют принципу симметрии кинетич. коэффициентов, выражающему симметрию ур-ний механики относительно изменения знака времени(см. Онсагера теорема).
Более общим понятием является обобщённая восприимчивость, описывающаяизменение
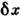 ср. значения нек-рой физ. величины х под действием малой «обобщённойсилы» f, к-рая входит в гамильтониан системы в виде
ср. значения нек-рой физ. величины х под действием малой «обобщённойсилы» f, к-рая входит в гамильтониан системы в виде 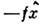 , где
, где 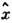 - квантовомеханич. оператор, соответствующий х. Если f зависитот времени как
- квантовомеханич. оператор, соответствующий х. Если f зависитот времени как 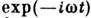 , изменение
, изменение 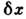 можно записать в виде
можно записать в виде 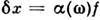 . Комплексная величина
. Комплексная величина 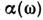 и есть обобщённая восприимчивость, она описывает поведение системы по отношениюк внеш. воздействию. С др. стороны, она определяет и релаксац. свойства:при
и есть обобщённая восприимчивость, она описывает поведение системы по отношениюк внеш. воздействию. С др. стороны, она определяет и релаксац. свойства:при 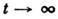 величина
величина 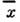 релаксирует к своему равновесному значению по закону
релаксирует к своему равновесному значению по закону 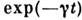 ,где
,где 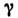 - расстояниеот вещественной оси до ближайшей к ней особенности ф-ции
- расстояниеот вещественной оси до ближайшей к ней особенности ф-ции 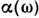 в нижней полуплоскости комплексной переменной w. К числу задач С. ф. неравновесныхпроцессов относится и исследование зависимости флуктуации от времени. Этазависимость описывается временной корреляц. ф-цией
в нижней полуплоскости комплексной переменной w. К числу задач С. ф. неравновесныхпроцессов относится и исследование зависимости флуктуации от времени. Этазависимость описывается временной корреляц. ф-цией 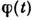 ,в к-рой усредняются флуктуации величины х, взятые в разл. моментывремени t:
,в к-рой усредняются флуктуации величины х, взятые в разл. моментывремени t: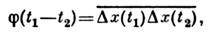
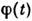 является чётной ф-цией своего аргумента. В классической С. ф. существуетсвязь между
является чётной ф-цией своего аргумента. В классической С. ф. существуетсвязь между 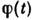 и законом релаксации величины
и законом релаксации величины 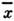 .Если релаксация описывается нек-рым линейным дифференц. ур-нием для отклонения
.Если релаксация описывается нек-рым линейным дифференц. ур-нием для отклонения 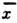 от равновесного значения, то тому же ур-нию удовлетворяет и
от равновесного значения, то тому же ур-нию удовлетворяет и 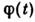 при t
при tСоотношение между
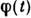 и
и 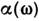 устанавливает флуктуационно-диссипативная теорема. Теорема утверждает, что фурье-образкорреляц. ф-ции
устанавливает флуктуационно-диссипативная теорема. Теорема утверждает, что фурье-образкорреляц. ф-ции 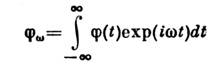
выражается через
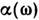 следующим образом:
следующим образом: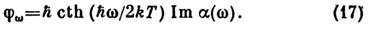
Частным случаем (17) является Найквиста формула. Описание сильнонеравновесных состояний, а также вычисление кинетич. коэф. производятсяс помощью кинетического уравнения Больцмана. Это ур-ние представляетсобой интегродифференц. ур-ние для одночастичной ф-ции распределения (вквантовом случае - для одночастичной матрицы плотности, или статистич. оператора). Оно содержит члены двух типов. Одни описывают изменение ф-циираспределения при движении частиц во внеш. полях, другие - при столкновенияхчастиц. Именно столкновения приводят к возрастанию энтропии неравновеснойсистемы, т. е. к релаксации. Замкнутое, т. е. не содержащее др. величинкинетич. ур-ние, невозможно получить в общем виде. При его выводе необходимоиспользовать малые параметры, имеющиеся в данной конкретной задаче. Важнейшимпримером является кинетич. ур-ние, описывающее установление равновесияв газе за счёт столкновений между молекулами. Оно справедливо для достаточноразреженных газов, когда длина свободного пробега велика по сравнению срасстояниями между молекулами. Конкретный вид этого ур-ния зависит от эфф. сечения рассеяния молекул друг на друге. Если это сечение известно, ур-ниеможно решать, разлагая искомую ф-цию по ортогональным полиномам. Такимспособом можно вычислить кинетич. коэф. газа, исходя из известных законоввзаимодействия между молекулами. Кинетич. ур-ние учитывает только парныестолкновения между молекулами и описывает только первый неисчезающий членразложения этих коэф. по плотности газа. Удалось найти и более точное ур-ние, учитывающее также тройные столкновения, что позволило вычислить следующийчлен разложения.
Особую проблему представляет вывод кинетич. ур-ния для плазмы. Из-замедленною убывания ку-лоновских сил с расстоянием даже при рассмотрениипарных столкновений существенно экранирование этих сил остальными частицами. Неравновесные состояния твёрдых тел и квантовых жидкостей можно при низкихтемп-pax рассматривать как неравновесные состояния газа соответствующихквазичастиц. Поэтому кинетич. процессы в таких системах описываются кинетич. ур-ниями для квазичастиц, учитывающими столкновения между ними и процессыих взаимного превращения. Новые возможности открыло применение в физ. кинетикеметодов квантовой теории поля. Кинетич. коэф. системы можно выразить черезеё ф-цию Грина, для к-рой существует общий способ вычисления с помощьюдиаграмм. Это позволяет в ряде случаев получить кинетич. коэф. без явногоиспользования кинетич. ур-ния и исследовать неравновесные свойства системыдаже в тех случаях, когда не выполняются условия его применимости.
Основные вехи развития статистической физики. С. ф. целиком основанана представлениях об атомном строении материи. Поэтому нач. период развитияС. ф. совпадает с развитием атомистич. представлений. Развитие С. ф. какраздела теорстич. физики началось в сер. 19 в. В 1859 Дж. Максвелл (J.Maxwell) определил ф-цию распределения молекул газа по скоростям. В 1860-70Р. Клаузиус (R. Clausing) ввёл понятие длины свободного пробега и связалеё с вязкостью и теплопроводностью газа. Примерно в то же время Л. Больцман(L. Boltzmann) обобщил распределение Максвелла на случай, когда газ находитсяво внеш. поле, доказал теорему о равнораспределении энергии по степенямсвободы, вывел кинетич. ур-ние, дал статистич. истолкование энтропии ипоказал, что закон её возрастания является следствием кинетич. ур-ния. Построение классической С. ф. было завершено к 1902 в работах Дж. У. Гиббса(J. W. Gibbs). Теория флуктуации была развита в 1905-06 в работах М. Смолуховского(М. Smoluchowski) и А. Эйнштейна (A. Einstein). В 1900 М. Планк (М. Planck)вывел закон распределения энергии в спектре излучения чёрного тела, положивначало развитию как квантовой механики, так и квантовой С. ф. В 1924 Ш. Бозе (Sh. Bose) нашёл распределение по импульсам световых квантов и связалего с распределением Планка. Эйнштейн обобщил распределение Бозе на газыс заданным числом частиц. Э. Ферми (Е. Fermi) в 1925 получил ф-цию распределениячастиц, подчиняющихся принципу Паули, а П. А. М. Дирак (Р. А. М. Dirac)установил связь этого распределения и распределения Бозе - Эйнштейна сматем. аппаратом квантовой механики. Дальнейшее развитие С. ф. в 20 в. шло под знаком приложения её осн. принципов к исследованию конкретных проблем.
Лит.: Ландау Л. Д., Л и ф ш и ц Е. М., Статистическая физика, ч. 1, 3 изд., М., 1976; М а й е р Д ж., Гепперт-Майер М., Статистическаямеханика, пер. с англ., 2 изд., М., 1980; Абрикосов А. А., Горькое Л. П.,Дзялошинский И. Е., Методы квантовой теории поля в статистической физике, М., 1962; X у а н г К., Статистическая механика, пер. с англ., М., 1966;К и т т е л ь Ч., Квантовая теория твердых тел, пер. с англ., М., 1967;Силин В. П., Введение в кинетическую теорию газов, М., 1971; Физика простыхжидкостей. Сб., пер. с англ., М., 1971; Ансельм А. И., Основы статистическойфизики и термодинамики, М., 1973; Л и ф ш и ц Е. М., Питаевский Л. П.,Статистическая физика, ч. 2, М., 1978; и х ж е, Физическая кинетика, М.,1979; Балеску Р., Равновесная и неравновесная статистическая ме-ханика, пер. с англ., т. 1-2, М., 1978; Боголюбов Н. Н., Избранные труды по статистическойфизике, М., 1979; Г и б б с Дж. В., Термодинамика. Статистическая механика, пер. с англ., М., 1982; Л е о н т о в и ч М. А., Введение в термодинамику. Статистическая физика, М., 1983; Больцман Л., Избранные труды, пер. с нем.,франц., М., 1984. Л. П. Питаевский.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.