- ТЕПЛОЁМКОСТЬ
-
количество теплоты, поглощаемой телом при нагревании на 1 градус (1°С или 1К); точнее — отношение кол-ва теплоты, поглощаемой телом при бесконечно малом изменении его темп-ры, к этому изменению. Т. ед. массы в-ва (г, кг) наз. удельной Т., 1 моля в-ва — молярной (мольной) Т. Ед. Т. служат Дж/(кг•К), Дж/(моль•К), Дж/(м3•К) и внесистемная ед. кал/(моль•К).Кол-во теплоты, поглощённой телом при изменении его состояния, зависит не только от начального и конечного состояний (в частности, от их темп-ры), но и от способа, к-рым был осуществлён процесс перехода между ними. Соответственно от способа нагревания тела зависит и его Т. Обычно различают Т. при пост. объёме (cv) и Т. при пост. давлении (ср), если в процессе нагревания поддерживаются постоянными соответственно его объём или давление. При нагревании при пост. давлении часть теплоты идёт на производство работы расширения тела, а часть — на увеличение его внутренней энергии, тогда как при нагревании при пост. объёме вся теплота расходуется на увеличение внутр. энергии; в связи с этим cp всегда больше, чем cv. Для газов (разреженных настолько, что их можно считать идеальными) разность мольных Т. ср-cv=R, где R — универс. газовая постоянная, равная 8,314 Д ж/(моль•К), или 1,986 кал/(моль•К). У жидкостей и тв. тел разница между ср и cv сравнительно мала.Из 1-го и 2-го начал термодинамики следует, что ср= Т(дS/дТ)р, а cv=T(дS/дT)v, т. е. Т. пропорц. производной от энтропии S системы по темп-ре Т при соответствующих условиях.Теор. вычисление Т., в частности её зависимости от темп-ры тела, не может быть осуществлено при помощи чисто термодинамич. методов и требует применения методов статистической физики (знания микроструктуры в-ва). Для газов вычисление Т. сводится к вычислению ср. энергии теплового движения отд. молекул. Это движение складывается из поступат. и вращат. движений молекулы как целого и из колебаний атомов внутри молекулы. Согласно классич. статистике, на каждую степень свободы поступат. и вращат. движений приходится в мольной Т. (сv) газа величина, равная R/2, а на каждую колебат. степень свободы — R; это правило наз. равнораспределения законом. Ч-ца одноатомного газа обладает всего тремя поступат. степенями свободы, соответственно его Т. сv должна составлять 3R/2 (т. е. ок. 12,5 Дж/(моль•К), или 3 кал/(моль•град)), что хорошо согласуется с опытом. Молекула двухатомного газа обладает тремя поступательными, двумя вращат. и одной колебат. степенями свободы, и закон равнораспределения приводит к значению сv=7R/2; опыт показывает, что Т. моля двухатомного газа (при обычных темп-рах) составляет 5R/2. Ото расхождение теории и эксперимента связано с тем, что при вычислении Т. необходимо учитывать квантовые эффекты, т. е. пользоваться квантовой статистикой. Согласно квантовой механике, всякая система ч-ц, совершающих колебания или вращения (в т. ч. молекула газа), может обладать лишь определёнными дискретными значениями энергии. Если энергия теплового движения в системе недостаточна для возбуждения колебаний определённой частоты, то эти колебания не вносят своего вклада в Т. системы (соответствующая степень свободы оказывается «замороженной» — к ней неприменим закон равнораспределения). Темп-ра Т, при достижении к-рой закон равнораспределения оказывается применимым к вращат. или колебат. степени свободы, определяется квантовомеханич. соотношением Т ->hn/k, где n — частота колебаний.Интервалы между вращат. уровнями энергии двухатомной молекулы (делённые на k) составляют всего неск. К и лишь для такой лёгкой молекулы, как молекула водорода, достигают сотни К. Поэтому при обычных темп-рах вращат. часть Т. двухатомных (а также многоатомных) газов подчиняется закону равнораспределения. Интервалы же между колебат. уровнями энергии достигают неск. тысяч К, и поэтому при обычных темп-рах закон равнораспределения неприменим к колебат. части Т. Вычисление Т. по квантовой статистике приводит к результату, что колебат. Т. быстро убывает при понижении темп-ры, стремясь к нулю. Этим объясняется то обстоятельство, что уже при обычных темп-рах колебат. часть Т. практически отсутствует и Т. моля двухатомного газа равна 5R/2 вместо 7R/2.При достаточно низких темп-рах Т. вообще должна вычисляться с помощью квантовой статистики. Как оказывается, Т. убывает с понижением темп-ры к нулю при Т ®0 в согласии с т. н. принципом Нернста (третьим началом термодинамики).В тв. (кристаллич.) телах тепловое движение атомов представляет собой малые колебания вблизи определённых положений равновесия (узлов крист. решётки). Каждый атом обладает, т. о., тремя колебат. степенями свободы, и, согласно закону равнораспределения, мольная Т. тв. тела (Т. крист. решётки) должна быть равной 3nR, где n — число атомов в молекуле. В действительности, однако, это значение — лишь предел, к к-рому стремится Т. тв. тела при высоких темп-рах. Он достигается уже при обычных темп-рах у мн. элементов, в т. ч. металлов (n=1, т. н. Дюлонга и Пти закон) к у нек-рых простых соединений (NaCl, MnS(n=2), PbCl2(n=3) и др.); у сложных соединений этот предел фактически не достигается, т. к. раньше наступает плавление в-ва или его разложение.ТЕПЛОЁМКОСТЬ ср НЕК-РЫХ ГАЗОВ (в Дж/(моль•К), ЖИДКОСТЕЙ И ТВЁРДЫХ ТЕЛ (в кДж/(кг•К) ПРИ ATM. ДАВЛЕНИИ И ПРИ t=25°С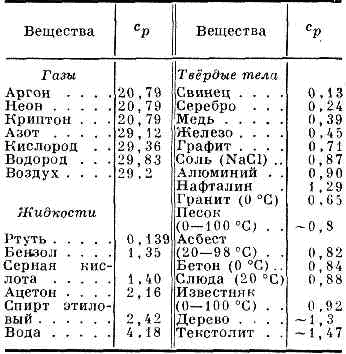 При низких темп-рах решёточная составляющая Т. тв. тела оказывается пропорц. кубу абс. темп-ры (Дебая закон теплоёмкости). Критерием, позволяющим различать высокие и низкие темп-ры, явл. сравнение их с характерным для каждого данного в-ва параметром — т. н. характеристической, или дебаевской, темп-рой qД. Эта величина определяется спектром колебания атомов в теле и тем самым существенно зависит от его крист. структуры (см. КОЛЕБАНИЯ КРИСТАЛЛИЧЕСКОЙ РЕШЁТКИ). Обычно 6д — величина порядка неск. сот К, но может достигать (напр., у алмаза) и тысяч К (см. ДЕБАЯ ТЕМПЕРАТУРА).У металлов определённый вклад в Т. дают также и эл-ны проводимости (т. н. электронная Т.). Эта часть Т. может быть вычислена с помощью квантовой статистики Ферми, к-рой подчиняются эл-ны. Электронная Т. металла пропорц. первой степени абс. темп-ры. Она представляет собой, однако, сравнительно малую величину, её вклад в Т. металла становится существенным лишь при темп-рах, близких к абс. нулю (порядка неск. К), когда решёточная Т. (= Т3) становится пренебрежимо малой. У крист. тел с упорядоченным расположением спиновых магн. моментов атомов (ферро- и антиферромагнетиков) существует дополнит. магн. составляющая Т. При темп-ре фазового перехода в парамагн. состояние (в Кюри точке, или, соответственно, Нееля точке) эта составляющая Т. испытывает резкий подъём -наблюдается «пик» Т., что явл. характерной особенностью фазовых переходов II рода.
При низких темп-рах решёточная составляющая Т. тв. тела оказывается пропорц. кубу абс. темп-ры (Дебая закон теплоёмкости). Критерием, позволяющим различать высокие и низкие темп-ры, явл. сравнение их с характерным для каждого данного в-ва параметром — т. н. характеристической, или дебаевской, темп-рой qД. Эта величина определяется спектром колебания атомов в теле и тем самым существенно зависит от его крист. структуры (см. КОЛЕБАНИЯ КРИСТАЛЛИЧЕСКОЙ РЕШЁТКИ). Обычно 6д — величина порядка неск. сот К, но может достигать (напр., у алмаза) и тысяч К (см. ДЕБАЯ ТЕМПЕРАТУРА).У металлов определённый вклад в Т. дают также и эл-ны проводимости (т. н. электронная Т.). Эта часть Т. может быть вычислена с помощью квантовой статистики Ферми, к-рой подчиняются эл-ны. Электронная Т. металла пропорц. первой степени абс. темп-ры. Она представляет собой, однако, сравнительно малую величину, её вклад в Т. металла становится существенным лишь при темп-рах, близких к абс. нулю (порядка неск. К), когда решёточная Т. (= Т3) становится пренебрежимо малой. У крист. тел с упорядоченным расположением спиновых магн. моментов атомов (ферро- и антиферромагнетиков) существует дополнит. магн. составляющая Т. При темп-ре фазового перехода в парамагн. состояние (в Кюри точке, или, соответственно, Нееля точке) эта составляющая Т. испытывает резкий подъём -наблюдается «пик» Т., что явл. характерной особенностью фазовых переходов II рода.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- ТЕПЛОЁМКОСТЬ
-
- кол-во теплоты; поглощаемой телом при нагревании на 1 градус (1 °С или 1 К); точнее - отношение кол-ва теплоты, поглощаемой телом при бесконечно малом изменении его темп-ры, к этому изменению. Т. единицы массы вещества наз. удельной Т., 1 моля вещества-молярной (мольной) Т. Единицами Т. служат Дж/(кг · К), ДжДмоль · К), Дж/(м 3 · К) и внесистемная единица кал/(моль·К).
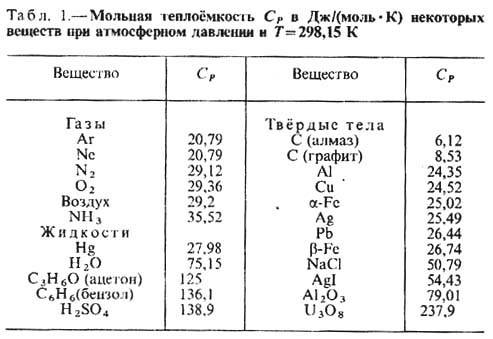
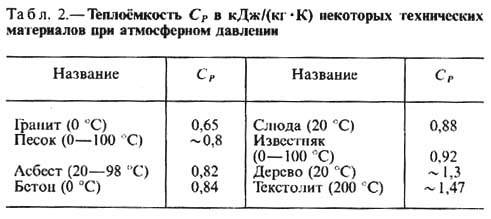
Кол-во теплоты, поглощённой телом при изменении его состояния, зависит не только от начального и конечного состояний (в частности, от их темп-ры), но и от способа, к-рым был осуществлён процесс перехода между ними. Соответственно от способа нагревания тела зависит и его Т. Обычно различают Т. при пост. объёме (CV )и Т. при пост. давлении ( С P), если в процессе нагревания поддерживаются постоянными соответственно объём тела или давление. При нагревании при пост. давлении часть теплоты идёт на производство работы расширения тела, а часть - на увеличение его внутренней энергии, тогда как при нагревании при пост. объёме вся теплота расходуется на увеличение внутр. энергии; в связи с этим С Р всегда больше, чем CV. Для газов (разреженных настолько, что их можно считать идеальными) разность мольных Т. С P - CV = R, где R- универсальная газовая постоянная, равная 8,314 Дж/(Дмоль·К) или 1,986 калДмоль·К). У жидкостей и твёрдых тел разница между С Р и CV сравнительно мала. Т. С Р нек-рых веществ и материалов приведены в табл. 1 и 2.
Из 1-го и 2-го начал термодинамики следует, что
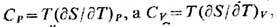 т. е. Т. пропорц. производной от энтропииS системы по темп-ре Т при соответствующих условиях.
т. е. Т. пропорц. производной от энтропииS системы по темп-ре Т при соответствующих условиях.
Теоретич. вычисление Т., в частности её зависимости от темп-ры тела, не может быть осуществлено при помощи чисто термодинамич. методов и требует применения методов статистической физики (знания микроструктуры вещества). Для газов вычисление Т. сводится к вычислению ср. энергии теплового движения отд. молекул. Это движение складывается из поступат. и вращат. движений молекулы как целого и из колебаний атомов внутри молекулы. Согласно классич. статистике, на каждую степень свободы поступат. и вращат. движений приходится в мольной Т. ( С V )газа величина, равная R/2, а на каждую колебат. степень свободы - R; это правило наз. равнораспределения законом. Частица одноатомного газа обладает всего тремя поступат. степенями свободы, соответственно его Т. С V должна составлять 3R/2 [т. е. ок. 12,5 ДжДмоль . К), или ~3 кал/(моль . К)], что хорошо согласуется с опытом. Молекула двухатомного газа обладает тремя поступат., двумя вращат. и одной колебат. степенями свободы, и закон равнораспределения приводит к значению CV =7R/2. опыт показывает, что Т. моля двухатомного газа (при обычных темп-pax) составляет 5R/2. Это расхождение теории и эксперимента связано с тем, что при вычислении Т. необходимо учитывать квантовые эффекты, т. е. пользоваться квантовой статистикой. Согласно квантовой механике, всякая система частиц, совершающих колебания или вращения (в т. ч. молекула газа), может обладать лишь определ. дискретными значениями энергии. Если энергия теплового движения в системе недостаточна для возбуждения колебаний определ. частоты, то эти колебания не вносят своего вклада в Т. системы (соответствующая степень свободы оказывается "замороженной" - к ней неприменим закон равнораспределения). Темп-pa Т, при достижении к-рой закон равнораспределения оказывается применимым к вращат. или колебат. степени свободы, определяется квантовомеханич. соотношением
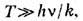 где v - частота колебаний.
где v - частота колебаний.
Интервалы между вращат. уровнями энергии двухатомной молекулы (делённые на k )составляют всего неск. К и лишь для такой лёгкой молекулы, как молекула водорода, достигают сотни К. Поэтому при обычных темп-рах вращат. часть Т. двухатомных (а также многоатомных) газов подчиняется закону равнораспределения. Интервалы же между колебат. уровнями энергии достигают неск. тысяч К, и поэтому при обычных темп-pax закон равнораспределения неприменим к колебат. части Т. Вычисление Т. по квантовой статистике приводит к результату, что колебат. Т. быстро убывает при понижении темп-ры, стремясь к нулю. Этим объясняется то обстоятельство, что уже при обычных темп-pax колебат. часть Т. практически отсутствует и Т. моля двухатомного газа равна 5R/2. вместо 7R/2.
При достаточно низких темп-pax Т. вообще должна вычисляться с помощью квантовой статистики. При T->0 Т. убывает в согласии с т. н. принципом Нернста ( третьим началом термодинамики),
В твёрдых (кристаллич.) телах тепловое движение атомов представляет собой малые колебания вблизи определ. положений равновесия (узлов кристаллич. решётки). Каждый атом обладает, т. о., тремя колебат. степенями свободы, и, согласно закону равнораспределения, мольная Т. твёрдого тела (Т. кристаллич. решётки) должна быть равной З nR, где n- число атомов в молекуле. В действительности, однако, это значение - лишь предел, к к-рому стремится Т. твёрдого тела при высоких темп-pax. Он достигается уже при обычных темп-pax у мн. элементов, в т. ч. у металлов (п=1, т. н. Дюлонга и Пти закон )и у нек-рых простых соединений [NaCl, MnS (n = 2), РbСl2 (n =3) и др. ]; у сложных соединений этот предел фактически не достигается, т. к. раньше наступает плавление вещества или его разложение.
При низких темп-pax решёточная составляющая Т, твёрдого тела оказывается пропорц. T3 ( Дебая закон теплоёмкости). Критерием, позволяющим различать высокие и низкие темп-ры, является сравнение их с характерным для каждого данного вещества параметром - т. н. характеристической или Дебая температуройqD, Эта величина определяется спектром колебания атомов в теле и тем самым существенно зависит от его кристаллич. структуры (см. Колебания кристаллической решётки). Обычно qD -величина порядка неск. сотен К, но может достигать (напр., у алмаза) и тысяч К,
У металлов определ. вклад в Т. дают также и электроны проводимости (см. Электронная теплоёмкость). Эта часть Т. может быть вычислена с помощью Ферми - Дирака, статистики, к-рой подчиняются электроны. Электронная Т. металла пропорц. Т. Она представляет собой, однако, сравнительно малую величину, её вклад в Т. металла становится существенным лишь при темп-pax, близких к абс, нулю (порядка неск. К), когда решёточная Т. (~Т3 )становится пренебрежимо малой. У кристаллич. тел с упорядоченным расположением спиновых магн. моментов атомов (ферро- и антиферромагнетиков) существует дополнит. магн, составляющая Т. При темп-ре фазового перехода в парамагн. состояние (в Кюри точке или соответственно Нееля точке )эта составляющая Т. испытывает резкий подъём - наблюдается "пик" Т., что является характерной особенностью фазовых переходов 2-го рода. .
Лит..: Ландау Л. Д., Лифшиц Е. М., Статистическая физика, 3 изд., ч. 1, М., 1976; Таблицы физических величин. Справочник, под ред. И. К. Кикоина, М., 1976. E. М. Лифшиц.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.