- ПОТЕНЦИАЛ
-
(потенциальная функция) (от лат. potentia — сила), хар-ка векторных полей, к к-рым относятся мн. силовые поля (эл.-магн., гравитационное), а также поле скоростей в жидкости и т. п. Если П. векторного поля а(r) — скалярная ф-ция j(r), такая, что a=gradj, то поле а, наз. потенциальным (иногда П. наз. ф-цию U=-j). П. j определяется с точностью до пост. слагаемого. Потенциальное поле № удовлетворяет Пуассона уравнению, для него выполняется условие rota=0. Если для поля а можно ввести в е к т о р н ы й п о т е н ц и а л А(r), такой, что a=rotA, поле а наз. соленоидальным. Для такого поля выполняется условие divа=0, А(r) в этом случае определяется с точностью до градиента от произвольной ф-ции (калибровочная, или градиентная инвариантность; (см. ПОТЕНЦИАЛЫ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ). В общем случае векторное поле можно представить в виде суммы потенциального и соленоидального полей. Понятие П. существенно для описания вз-ствия ч-цы с полем и отыскания полей по заданным распределениям их источников.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- ПОТЕНЦИАЛ
-
(потенциальная функция) (от лат. рo-tentia - сила) - характеристика векторных полей, к к-рым относятся многие силовые поля (эл.-магн.,. гравитационное), а также поле скоростей в жидкости и др. Если П. векторного поля
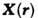 есть скалярная ф-ция
есть скалярная ф-ция 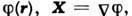 то поле X наз. потенциальным (иногда П. наз. ф-цию
то поле X наз. потенциальным (иногда П. наз. ф-цию 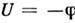 ). П.
). П.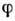 определён с точностью до пост. величины. Для потенц. поля
определён с точностью до пост. величины. Для потенц. поля 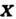 справедливо условие
справедливо условие 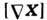 = 0, и обратно, если для нек-рого поля
= 0, и обратно, если для нек-рого поля 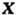 всюду
всюду 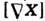 = 0, то поле
= 0, то поле 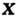 - потенциально, для него существует П.
- потенциально, для него существует П.Если векторное поле
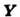 соленоидально, т. е.
соленоидально, т. е.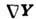 = О, то для этого поля можно ввести векторный потенциал
= О, то для этого поля можно ввести векторный потенциал 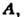 такой, что
такой, что 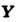 =
=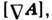 при этомопределён
при этомопределён 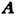 с точностью до градиента произвольной ф-ции ( градиентная инвариантность). В общем случае любое векторное поле представляется суммой потенциального и соле-ноидального полей.
с точностью до градиента произвольной ф-ции ( градиентная инвариантность). В общем случае любое векторное поле представляется суммой потенциального и соле-ноидального полей.В классич. и квантовой физике измеряемыми на опыте являются силовые характеристики полей - их напряжённости. На первый взгляд представляется, что сами по себе потенциалы полей не несут физ. смысл, а их введение в теорию - не более чем удобный техн. приём. Оказывается, однако, что в квантовой механике возникают эффекты ( квантование магнитного потока, Ааронова - Бома эффект, Джозефсона эффект, эффект Казимира), в к-рых физ. природа П. проявляется непосредственно. Все эти эффекты имеют наглядную геом. интерпретацию. Векторный потенциал представляет собой связность в расслоении, базой к-ро-го служит соответствующее пространство (напр., пространство Минковского M4). В квантовой теории поля осн. объект исследования - квантовые поля - являются аналогами классич. П., т. к. набор потенциальных ф-ций - мин. набор независимых динамич. переменных, полностью описывающий систему. Напр., в квантовой электродинамике такими переменными будут квантовые поля (потенциалы)
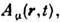 где 4-компо-нентный вектор
где 4-компо-нентный вектор 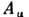 задаётся потенциалами
задаётся потенциалами 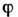 и
и 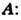
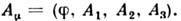
Лит.: Тамм И. П., Основы теории электричества, 10 изд., М., 1989; Ландау Л. Д., Лифшиц E. М., Теория поля, 7 изд., М., 1988; Славное А. А., Фаддеев Л. Д., Введение в квантовую теорию калибровочных полей, 2 изд., М., 1988. Л. О. Чехов.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.