- ЭРГОДИЧЕСКАЯ ГИПОТЕЗА
-
в статистической физике, состоит в предположении, что средние по времени значения физ. величин, характеризующих систему, равны их средним статистич. значениям; служит для обоснования статистич. физики. Физ. системы, для к-рых справедлива Э. г., наз. э р г о д и ч е с к и м и. Точнее, в классич. статистич. физике равновесных систем Э, г. есть предположение о том, что средние по времени от т. н. фазовых переменных (ф-ций, зависящих от координат и импульсов всех ч-ц системы), взятые по траектории движения системы как точки в фазовом пространстве (фазовой точки), равны средним статистическим по равномерному распределению фазовых точек в тонком (в пределе бесконечно тонком) слое вблизи поверхности пост. энергии. Такое распределение наз. микроканоническим распределением Гиббса.В квант. статистич. физике Э. г. есть предположение, что все энергетич. состояния в тонком слое вблизи поверхности пост. энергии равновероятны. Э. г. эквивалентна, т. о., предположению, что замкнутая система может быть описана микроканонич. распределением Гиббса. Это один из осн. постулатов равновесной статистич. физики, т. к. на основании микроканонич. распределения могут быть получены канонич. и большое канонич. распределения Гиббса (см. ГИББСА РАСПРЕДЕЛЕНИЯ).В более узком смысле Э. г.— выдвинутое австр. физиком Л. Больцманом в 70-х гг. 19 в. предположение о том, что фазовая траектория замкнутой системы с течением времени проходит через любую точку поверхности пост. энергии в фазовом пр-ве. В такой форме Э. г. неверна, т. к. ур-ния Гамильтона (см. КАНОНИЧЕСКИЕ УРАВНЕНИЯ МЕХАНИКИ) однозначно определяют касательную к фазовой траектории и не допускают самопересечения фазовых траекторий. Поэтому вместо больцмановской Э. г. была выдвинута квазиэргодическая гипотеза, в к-рой предполагается, что фазовые траектории замкнутой системы сколь угодно близко подходят к любой точке поверхности пост. энергии.Матем. эргодич. теория изучает, при каких условиях средние по времени для ф-ций фазовых переменных динамич. системы равны средним статистическим. Согласно эргодич. теореме амер. математика Дж. Неймана, система эргодична при условии, что энергетич. поверхность не может быть разделена на такие конечные области, в к-рых вместе с начальной фазовой точкой находилась бы и вся фазовая траектория (т. н. св-во метрич. неразложимости). Доказательство того, что реальные системы явл. эргодическими,— очень сложная и ещё не решённая проблема.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- ЭРГОДИЧЕСКАЯ ГИПОТЕЗА
-
в с т а т и с т и ч е с к о й ф и з и к е - предположение, что с р е д н и е п о в р е м е н и значения физ. величин, характеризующих систему, равны их с р е д н и м с т а т и с т и ч е с к и м. Предложена Л. Больцманом в 1887 для обоснования статистической фи зики.
В классич. статистич. физике равновесных систем Э. г. основана на предположении, что средние по времени от фазовых переменных (ф-ций, зависящих от координат q и импульсов р всех частиц замкнутой и энергетически изолированной системы), взятые вдоль траектории движения системы в фазовом пространстве, равны средним статистическим по равномерному распределению фазовых точек в тонком (в пределе - бесконечно тонком) слое вблизи поверхности постоянной энергии. В квантовой статистич. физике Э. г. есть предположение, что все энергетич. состояния в тонком слое вблизи поверхности постоянной энергии равновероятны. Э. г. эквивалентна, т. о., предположению, что замкнутая система (как классическая, так и квантовая) может быть описана микроканоническим распределением Гиббса. Напр., для классических замкнутых систем из N частиц с Гамильтона функцией HN (p, q )в объёме V почти всегда существуют средние по времени от функции фазовых переменных F(p(t), q(t))
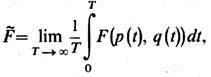
где эволюция р (t), q (t )во времени определяется из решения ур-ний Гамильтона. Согласно Э. г.,
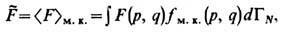
где d Г N=dpdq/N!h3N - элемент фазового объёма в безразмерных переменных; f м. к.( р, q)- микроканонич. распределение, имеющее вид
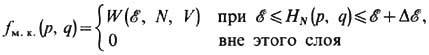
(интегрирование проводится по всем "микроскопическим" состояниям системы, энергия к-рых лежит в слое энергии шириной
); 
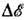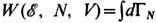- статистический вес, связанный с энтропией S соотношением S=kln W.
Делались попытки обоснования Э. г. с помощью исследования свойств фазовых траекторий замкнутых изолированных механич. систем из большого числа частиц. Были доказаны эргодические теоремы (см. Эргодическая теория), к-рые сводили Э. г. к предположению о специфич. свойстве фазового пространства (его метрической неразложимости). Однако для обоснования статистич. физики эти теоремы не являются необходимыми, т. к. фазовые траектории чрезвычайно чувствительны к малым возмущениям (см. Размешивание). В частности, они очень чувствительны к малейшему нарушению изоляции или замкнутости системы. Аналогичным свойством чувствительности квантовых состояний к малым возмущениям обладают и квантовые системы. Д. Н. Зубарев.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.