- ИЗЛУЧЕНИЕ
-
электромагнитное, в классич. электродинамике образование эл.-магн. волн ускоренно движущимися заряж. ч-цами (или перем. токами); в квант. теории рождение фотонов при изменении состояния квант. системы; термин «И.» употребляется также для обозначения самого свободного (т. е. излучённого) эл.-магн. поля. Основы классич. теории И. (электродинамики) заложены в 1-й пол. 19 в. англ. физиками М. Фарадеем и Дж. Максвеллом; последний развил идеи Фарадея и придал им строгую матем. форму. Классич. теория И. объяснила мн. характерные черты процессов И. (она осталась, напр., теор. базой электротехники и радиотехники), но не смогла дать удовлетворит. описания законов теплового излучения, спектров атомов и молекул. Эти и ряд др. проблем удалось решить лишь в рамках квант. теории И. Первая работа, положившая начало квант. теории И., принадлежит нем. физику М. Планку (1900), к-рый вывел ф-лу для распределения энергии в спектре равновесного теплового излучения, впервые приняв, что ат. системы испускают эл.-магн. волны не непрерывно, а порциями, квантами. Основы квант. теории излучения заложили А. Эйнштейн, дат. физик Н. Бор, франц. физик Л. де Бройль и др. Полное теор. обоснование она получила после создания квантовой электродинамики.Классическая теория излучения (теория Максвелла). Физ. причины существования свободного эл.-магн. поля (т. е. самоподдерживающегося, независимого от возбудивших его источников) тесно связаны с тем, что изменяющееся во времени электрич. поле Е порождает магн. поле Н, а изменяющееся Н — вихревое электрич. поле: обе компоненты Е и Н, непрерывно изменяясь, возбуждают друг друга. Благодаря конечности скорости распространения эл.-магн. поля, оно может существовать автономно от породившего его источника и не исчезает с устранением источника (напр., радиоволны не исчезают и при отсутствии тока в излучившей их антенне).В процессе И. эл.-магн. поле уносит от источника И. энергию. Плотность потока энергии этого поля определяется Пойнтинга вектором П, к-рый пропорционален векторному произведению (ЕН).Интенсивность И. ?и — энергия, уносимая полем от источника в ед. времени. Порядок её величины определяется ср. плотностью потока через к.-л. замкнутую поверхность (обычно выбирают сферическую радиуса R, её площадь =R ), и при R ®?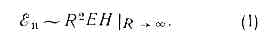 Для того чтобы эта величина не обращалась в нуль, т. е. для возможности существования свободного эл.-магн. поля, необходимо, чтобы Е и Н убывали не быстрее, чем 1/R. Это требование удовлетворяется для вихревой части поля, порождаемого ускоренно движущимися зарядами.И. движущегося заряда. Простейший источник поля — точечный заряд. У покоящегося или равномерно движущегося (в пустоте) заряда И. отсутствует. Излучает эл.-магн. волны лишь ускоренно движущийся заряд. Прямые вычисления на основе ур-ний Максвелла показывают, что интенсивность И. такого заряда равна:
Для того чтобы эта величина не обращалась в нуль, т. е. для возможности существования свободного эл.-магн. поля, необходимо, чтобы Е и Н убывали не быстрее, чем 1/R. Это требование удовлетворяется для вихревой части поля, порождаемого ускоренно движущимися зарядами.И. движущегося заряда. Простейший источник поля — точечный заряд. У покоящегося или равномерно движущегося (в пустоте) заряда И. отсутствует. Излучает эл.-магн. волны лишь ускоренно движущийся заряд. Прямые вычисления на основе ур-ний Максвелла показывают, что интенсивность И. такого заряда равна: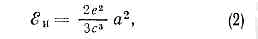 где е — величина заряда, а — его ускорение. В зависимости от природы ускорения заряж. ч-ц И. иногда имеет определ. название. Так, И., возникающее при торможении ч-ц в в-ве в результате воздействия на них кулоновских полей ядер и эл-нов атомов, наз. тормозным излучением. И. заряж. ч-цы, движущейся в магн. поле, может быть синхротронным излучением, ондуляторным излучением и т. д.В частном случае, когда заряд совершает гармонич. колебания, ускорение а по величине равно произведению отклонения х заряда от положения равновесия (z=x0sinwt, где х0 — амплитуда отклонения) на квадрат частоты со. Усреднённая по времени t интенсивность И.
где е — величина заряда, а — его ускорение. В зависимости от природы ускорения заряж. ч-ц И. иногда имеет определ. название. Так, И., возникающее при торможении ч-ц в в-ве в результате воздействия на них кулоновских полей ядер и эл-нов атомов, наз. тормозным излучением. И. заряж. ч-цы, движущейся в магн. поле, может быть синхротронным излучением, ондуляторным излучением и т. д.В частном случае, когда заряд совершает гармонич. колебания, ускорение а по величине равно произведению отклонения х заряда от положения равновесия (z=x0sinwt, где х0 — амплитуда отклонения) на квадрат частоты со. Усреднённая по времени t интенсивность И.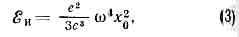 т. е. при увеличении частоты растет пропорц. w4.Электрическое дипольное И. Простейшей системой, к-рая может быть источником И., явл. электрич. диполь с перем. моментом: два связанных колеблющихся разноимённых заряда равной величины. Если заряды диполя совершают гармонич. колебания навстречу друг другу, то дипольный электрич. момент d изменяется по закону: d=d0sinwt (d0 — амплитуда момента). Усреднённая по времени t интенсивность И. такого диполя ?эл дип равна:
т. е. при увеличении частоты растет пропорц. w4.Электрическое дипольное И. Простейшей системой, к-рая может быть источником И., явл. электрич. диполь с перем. моментом: два связанных колеблющихся разноимённых заряда равной величины. Если заряды диполя совершают гармонич. колебания навстречу друг другу, то дипольный электрич. момент d изменяется по закону: d=d0sinwt (d0 — амплитуда момента). Усреднённая по времени t интенсивность И. такого диполя ?эл дип равна: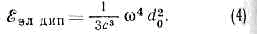 И. колеблющегося диполя неизотропно, т. е. энергия, испускаемая им в разл. направлениях, неодинакова. Вдоль оси колебаний И. отсутствует, в перпендикулярном к оси направлении — максимально; для промежуточных направлений оно пропорц. sinq2, где q — угол, отсчитываемый от оси колебаний.Реальные излучатели, как правило, включают множество зарядов. Точный учёт всех деталей движения каждого из них при исследовании И. излишен, т. к. детали распределения зарядов (и токов) в излучателе вдали от него сказываются слабо. Это позволяет заменять истинное распределение зарядов приближённым. В низшем приближении положит. и отрицат. заряды излучающей системы мысленно «стягиваются» к центрам своего распределения. Для электронейтральной системы это означает замену её электрич. диполем, излучающим согласно (4). Такое приближение наз. дипольным, а соответствующее И.— электрическим дипольным И.Электрическое квадрупольное и высшие мультипольные И. Если у системы зарядов дипольное И. отсутствует, напр. из-за равенства нулю дипольного момента, то необходимо учитывать след. приближение, в к-ром система зарядов рассматривается как квадруполь. Ещё более детальное описание излучающей системы зарядов даёт рассмотрение последующих приближений, в к-рых распределение зарядов описывается мулътиполями высших порядков (диполь наз. мультиполем 1-го порядка, квадруполь — 2-го и т. д. порядков).В каждом последующем приближении интенсивность И. примерно в (v/с)2 меньше, чем в предыдущем (если, конечно, последнее не отсутствует по к.-л. причинам). Если излучатель нерелятивистский, т. е. все его заряды имеют скорости, много меньшие световой (v/с-1), то гл. роль играет низшее неисчезающее приближение. Так, если имеется дипольное И., оно явл. основным, а все остальные высшие мультипольные поправки крайне малы и их можно не учитывать. В случае релятив. излучателей вклад мультиполей высших порядков перестаёт быть малым.Магнитное дипольное И. Кроме электрич. диполей и высших мультиполей, источниками И. могут быть также магн. диполи и мультиполи (как правило, основным явл. дипольное магн. И.). Дипольный магн. момент М магн. диполя, напр. контура с током, определяется силой тока I в контуре и его геометрией. Для плоского контура абс. величина момента M=(e/c)IS, где S — площадь, охватываемая контуром. Ф-лы для интенсивности магн. дипольного И. аналогичны соответствующим ф-лам для И. электрич. диполя (дипольный момент d в них заменён На магн. дипольный момент М). Т. к. отношение М к d имеет порядок v/c, где v — скорость движения зарядов, образующих ток, интенсивность магн. дипольного И. в (v/c)2 раз меньше, чем электрического дипольного, т. е. того же порядка величины, что и электрич. квадрупольное И.И. релятивистских частиц. Пример такого И.— синхротронное И. эл-нов в циклич. ускорителях (синхротронах). Резкое отличие от нерелятив. И. проявляется здесь уже в спектр. составе И.: при частоте w обращения заряж. ч-цы в ускорителе (нерелятив. излучатель испускал бы волны такой же частоты) интенсивность И. имеет максимум при частоте wмякс=g3w, где g=(1-(v/c)2)-1/2, т. е. осн. доля И. при v®c приходится на частоты более высокие, чем со. Такое И. направлено почти по касательной к орбите ч-цы, в осн. вперёд по направлению её движения.Ультрарелятив. заряж. ч-ца может излучать эл.-магн. волны, даже если она движется прямолинейно и равномерно (но только в в-ве, а не в пустоте!). Это т. н. Черенкова — Вавилова излучение возникает в том случае, если скорость заряж. ч-цы в среде превосходит фазовую скорость света в этой среде u=с/n, где n — показатель преломления среды. И. появляется вследствие того, что ч-ца «обгоняет» порождаемое ею поле. Излучает также равномерно движущаяся заряж. ч-ца при пересечении границы раздела двух сред с разными показателями преломления (см. ПЕРЕХОДНОЕ ИЗЛУЧЕНИЕ).Квантовая теория излучения. Выше отмечалось, что классич. теория даёт лишь приближённое описание процессов И. Однако существуют и такие физ. системы, И. к-рых невозможно описать в согласии с опытом на основе классич. электродинамики даже приближённо. Важная особенность таких квант. систем, как атом или молекула, заключается в том, что их внутр. энергия меняется не непрерывно, а может принимать лишь определ. значения, образующие дискр. набор. Переход системы из одного энергетич. состояния в другое (см. КВАНТОВЫЙ ПЕРЕХОД) происходит скачкообразно; в силу закона сохранения энергии, система при таком переходе должна терять или приобретать определ. «порцию» энергии. Чаще всего этот процесс реализуется в виде испускания (или поглощения) системой кванта И.— фотона. Энергия кванта eg=hw. Фотон, обладая волн. св-вами, проявляется как единое целое, испускается и поглощается целиком, в одном акте, имеет определённые энергию, импульс и спин (проекцию момента кол-ва движения на направление импульса), т. е. обладает рядом корпускулярных св-в. Такая двойственность фотона представляет собой частное проявление корпускулярно-волнового дуализма.Последоват. развитием квант. теории И. явл. квантовая электродинамика. Однако мн. результаты, относящиеся к процессам И. квант. систем, можно получить из более простой, полуклассической теории И. Ф-лы последней, согласно соответствия принципу, при определённом предельном переходе должны давать результаты классич. теории. Т. о. устанавливается глубокая аналогия между величинами, характеризующими процессы И. в квант. и классич. теориях.И. атома. Атом — система из ядра и движущихся в его кулоновском поле эл-нов — должен находиться в одном из дпскр. состояний (на определ. уровне энергии). При этом все его состояния, кроме основного (т. е. имеющего наименьшую энергию), неустойчивы. Атом, находящийся в неустойчивом (возбуждённом) состоянии, через нек-рое время самопроизвольно (спонтанно) переходит в состояние с меньшей энергией, испуская фотон; такое И. наз. спонтанным. Энергия, уносимая фотоном, eg=hw, равна разности энергий нач. i и кон. j состояний атома (ei>ej, eg=ei-ej); отсюда вытекает ф-ла Бора для частот И.:
И. колеблющегося диполя неизотропно, т. е. энергия, испускаемая им в разл. направлениях, неодинакова. Вдоль оси колебаний И. отсутствует, в перпендикулярном к оси направлении — максимально; для промежуточных направлений оно пропорц. sinq2, где q — угол, отсчитываемый от оси колебаний.Реальные излучатели, как правило, включают множество зарядов. Точный учёт всех деталей движения каждого из них при исследовании И. излишен, т. к. детали распределения зарядов (и токов) в излучателе вдали от него сказываются слабо. Это позволяет заменять истинное распределение зарядов приближённым. В низшем приближении положит. и отрицат. заряды излучающей системы мысленно «стягиваются» к центрам своего распределения. Для электронейтральной системы это означает замену её электрич. диполем, излучающим согласно (4). Такое приближение наз. дипольным, а соответствующее И.— электрическим дипольным И.Электрическое квадрупольное и высшие мультипольные И. Если у системы зарядов дипольное И. отсутствует, напр. из-за равенства нулю дипольного момента, то необходимо учитывать след. приближение, в к-ром система зарядов рассматривается как квадруполь. Ещё более детальное описание излучающей системы зарядов даёт рассмотрение последующих приближений, в к-рых распределение зарядов описывается мулътиполями высших порядков (диполь наз. мультиполем 1-го порядка, квадруполь — 2-го и т. д. порядков).В каждом последующем приближении интенсивность И. примерно в (v/с)2 меньше, чем в предыдущем (если, конечно, последнее не отсутствует по к.-л. причинам). Если излучатель нерелятивистский, т. е. все его заряды имеют скорости, много меньшие световой (v/с-1), то гл. роль играет низшее неисчезающее приближение. Так, если имеется дипольное И., оно явл. основным, а все остальные высшие мультипольные поправки крайне малы и их можно не учитывать. В случае релятив. излучателей вклад мультиполей высших порядков перестаёт быть малым.Магнитное дипольное И. Кроме электрич. диполей и высших мультиполей, источниками И. могут быть также магн. диполи и мультиполи (как правило, основным явл. дипольное магн. И.). Дипольный магн. момент М магн. диполя, напр. контура с током, определяется силой тока I в контуре и его геометрией. Для плоского контура абс. величина момента M=(e/c)IS, где S — площадь, охватываемая контуром. Ф-лы для интенсивности магн. дипольного И. аналогичны соответствующим ф-лам для И. электрич. диполя (дипольный момент d в них заменён На магн. дипольный момент М). Т. к. отношение М к d имеет порядок v/c, где v — скорость движения зарядов, образующих ток, интенсивность магн. дипольного И. в (v/c)2 раз меньше, чем электрического дипольного, т. е. того же порядка величины, что и электрич. квадрупольное И.И. релятивистских частиц. Пример такого И.— синхротронное И. эл-нов в циклич. ускорителях (синхротронах). Резкое отличие от нерелятив. И. проявляется здесь уже в спектр. составе И.: при частоте w обращения заряж. ч-цы в ускорителе (нерелятив. излучатель испускал бы волны такой же частоты) интенсивность И. имеет максимум при частоте wмякс=g3w, где g=(1-(v/c)2)-1/2, т. е. осн. доля И. при v®c приходится на частоты более высокие, чем со. Такое И. направлено почти по касательной к орбите ч-цы, в осн. вперёд по направлению её движения.Ультрарелятив. заряж. ч-ца может излучать эл.-магн. волны, даже если она движется прямолинейно и равномерно (но только в в-ве, а не в пустоте!). Это т. н. Черенкова — Вавилова излучение возникает в том случае, если скорость заряж. ч-цы в среде превосходит фазовую скорость света в этой среде u=с/n, где n — показатель преломления среды. И. появляется вследствие того, что ч-ца «обгоняет» порождаемое ею поле. Излучает также равномерно движущаяся заряж. ч-ца при пересечении границы раздела двух сред с разными показателями преломления (см. ПЕРЕХОДНОЕ ИЗЛУЧЕНИЕ).Квантовая теория излучения. Выше отмечалось, что классич. теория даёт лишь приближённое описание процессов И. Однако существуют и такие физ. системы, И. к-рых невозможно описать в согласии с опытом на основе классич. электродинамики даже приближённо. Важная особенность таких квант. систем, как атом или молекула, заключается в том, что их внутр. энергия меняется не непрерывно, а может принимать лишь определ. значения, образующие дискр. набор. Переход системы из одного энергетич. состояния в другое (см. КВАНТОВЫЙ ПЕРЕХОД) происходит скачкообразно; в силу закона сохранения энергии, система при таком переходе должна терять или приобретать определ. «порцию» энергии. Чаще всего этот процесс реализуется в виде испускания (или поглощения) системой кванта И.— фотона. Энергия кванта eg=hw. Фотон, обладая волн. св-вами, проявляется как единое целое, испускается и поглощается целиком, в одном акте, имеет определённые энергию, импульс и спин (проекцию момента кол-ва движения на направление импульса), т. е. обладает рядом корпускулярных св-в. Такая двойственность фотона представляет собой частное проявление корпускулярно-волнового дуализма.Последоват. развитием квант. теории И. явл. квантовая электродинамика. Однако мн. результаты, относящиеся к процессам И. квант. систем, можно получить из более простой, полуклассической теории И. Ф-лы последней, согласно соответствия принципу, при определённом предельном переходе должны давать результаты классич. теории. Т. о. устанавливается глубокая аналогия между величинами, характеризующими процессы И. в квант. и классич. теориях.И. атома. Атом — система из ядра и движущихся в его кулоновском поле эл-нов — должен находиться в одном из дпскр. состояний (на определ. уровне энергии). При этом все его состояния, кроме основного (т. е. имеющего наименьшую энергию), неустойчивы. Атом, находящийся в неустойчивом (возбуждённом) состоянии, через нек-рое время самопроизвольно (спонтанно) переходит в состояние с меньшей энергией, испуская фотон; такое И. наз. спонтанным. Энергия, уносимая фотоном, eg=hw, равна разности энергий нач. i и кон. j состояний атома (ei>ej, eg=ei-ej); отсюда вытекает ф-ла Бора для частот И.: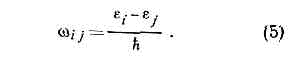 Такие хар-ки спонтанного И., как направление распространения (для совокупности атомов — угл. распределение) и поляризация, не зависят от И. др. объектов (от внеш. эл.-магн. поля).Ф-ла (5) определяет дискр. набор частот (и, следовательно, длин волн) И. атома. Она объясняет линейчатый хар-р атомных спектров — каждая линия спектра соответствует одному из квант. переходов атомов данного в-ва.Источниками эл.-магн. И. могут быть не только атомы, но и более сложные квант. системы. Общие методы описания И. таких систем те же, что при рассмотрении атомов, но конкретные особенности И. весьма разнообразны. И. молекул, напр., имеет более сложные спектры, чем И. атомов; для И. ат. ядер энергия отд. квантов (g-квантов) обычно велика.Интенсивность И. В квант. теории, как и в классической, можно рассматривать электрич. дипольное и высшие мультипольные И. Если излучатель нерелятивистский, основным явл. электрич. дипольное И., интенсивность к-рого определяется ф-лой, близкой к классической:
Такие хар-ки спонтанного И., как направление распространения (для совокупности атомов — угл. распределение) и поляризация, не зависят от И. др. объектов (от внеш. эл.-магн. поля).Ф-ла (5) определяет дискр. набор частот (и, следовательно, длин волн) И. атома. Она объясняет линейчатый хар-р атомных спектров — каждая линия спектра соответствует одному из квант. переходов атомов данного в-ва.Источниками эл.-магн. И. могут быть не только атомы, но и более сложные квант. системы. Общие методы описания И. таких систем те же, что при рассмотрении атомов, но конкретные особенности И. весьма разнообразны. И. молекул, напр., имеет более сложные спектры, чем И. атомов; для И. ат. ядер энергия отд. квантов (g-квантов) обычно велика.Интенсивность И. В квант. теории, как и в классической, можно рассматривать электрич. дипольное и высшие мультипольные И. Если излучатель нерелятивистский, основным явл. электрич. дипольное И., интенсивность к-рого определяется ф-лой, близкой к классической: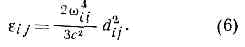 Величины dij, являющиеся квант. аналогом электрич. дипольного момента, оказываются отличными от нуля лишь при определ. соотношениях между квантовыми числами нач. и кон. состояний (отбора правила для дипольного И.). Квант. переходы, удовлетворяющие таким правилам отбора, наз. разрешёнными (фактически имеется в виду разрешённое электрическое дипольное И.). Переходы же высших мультипольностей наз. запрещёнными. Этот запрет относителен: запрещённые переходы имеют относительно малую вероятность, т. е. отвечающая им интенсивность И. невелика. Те состояния, переходы из к-рых запрещены, явл. сравнительно устойчивыми, долгоживущими и наз. метастабильными состояниями.Квант. теория И. позволяет объяснить не только различие в интенсивностях разных линий, но и распределение интенсивности в пределах каждой линии, в частности ширину спектральных линий.Эл.-магн. И. часто возникает и при взаимных превращениях элем. ч-ц (аннигиляция эл-нов и позитронов, распад p°-мезона и т. д.).Вынужденное И. Если частота И., падающего на уже возбуждённый атом, совпадает с одной из частот возможных для этого атома, согласно (5), квант. переходов, то атом испускает квант И., такой же, как и налетевший на него (резонансный) фотон внеш. И. Это И. наз. вынужденным. По своим св-вам оно резко отличается от спонтанного — не только частота, но и направление распространения, и поляризация испущенного фотона оказываются такими же, как и у резонансного. Вероятность вынужденного И. (в отличие от спонтанного) пропорц. интенсивности внеш. И., т. е. кол-ву резонансных фотонов. Существование вынужденного И. было постулировано Эйнштейном в 1916 при теор. анализе процессов теплового И. тел с позиций квант. теории и затем было подтверждено экспериментально. В обычных условиях интенсивность вынужденного И. мала по сравнению с интенсивностью спонтанного. Однако она сильно возрастает в т. н. активной среде, в к-рой искусственно создана инверсия населённостей, т. е. в одном из возбуждённых состояний находится больше атомов, чем в одном из состояний с меньшей энергией. При попадании в такую среду резонансного фотона испускаются фотоны, в свою очередь играющие роль резонансных. Число излучаемых фотонов лавинообразно возрастает; результирующее И. состоит из фотонов, идентичных по своим св-вам, т. е. образуется когерентный поток И. (см. КОГЕРЕНТНОСТЬ). На этом явлении основано действие квантовых генераторов и квантовых усилителей И.Значение теории излучения. Практич. и научно-прикладное значение теории И. огромно. На ней основываются разработка и применение лазеров и мазеров, создание новых источников света, ряд важных достижений в области радиотехники и спектроскопии. Понимание и изучение законов И. важно и в др. отношении: по хар-ру И. (энергетич. спектру, угл. распределению, поляризации) можно судить о св-вах излучателя. Эл.-магн. И.— пока фактически единственный и весьма многосторонний источник информации о косм. объектах. Напр., анализ И., приходящего из космоса, позволил открыть такие необычные небесные тела, как пульсары. Изучение спектров далёких внегалактич. объектов подтвердило теорию расширяющейся Вселенной. С другой стороны, исследование И. позволило решить мн. вопросы строения в-ва. Именно теории И. принадлежит особая роль в формировании всей совр. физ. картины мира: преодоление трудностей, возникших в электродинамике движущихся сред, привело к созданию относительности теории; исследования Планком теплового излучения положили начало всей квант. теории.
Величины dij, являющиеся квант. аналогом электрич. дипольного момента, оказываются отличными от нуля лишь при определ. соотношениях между квантовыми числами нач. и кон. состояний (отбора правила для дипольного И.). Квант. переходы, удовлетворяющие таким правилам отбора, наз. разрешёнными (фактически имеется в виду разрешённое электрическое дипольное И.). Переходы же высших мультипольностей наз. запрещёнными. Этот запрет относителен: запрещённые переходы имеют относительно малую вероятность, т. е. отвечающая им интенсивность И. невелика. Те состояния, переходы из к-рых запрещены, явл. сравнительно устойчивыми, долгоживущими и наз. метастабильными состояниями.Квант. теория И. позволяет объяснить не только различие в интенсивностях разных линий, но и распределение интенсивности в пределах каждой линии, в частности ширину спектральных линий.Эл.-магн. И. часто возникает и при взаимных превращениях элем. ч-ц (аннигиляция эл-нов и позитронов, распад p°-мезона и т. д.).Вынужденное И. Если частота И., падающего на уже возбуждённый атом, совпадает с одной из частот возможных для этого атома, согласно (5), квант. переходов, то атом испускает квант И., такой же, как и налетевший на него (резонансный) фотон внеш. И. Это И. наз. вынужденным. По своим св-вам оно резко отличается от спонтанного — не только частота, но и направление распространения, и поляризация испущенного фотона оказываются такими же, как и у резонансного. Вероятность вынужденного И. (в отличие от спонтанного) пропорц. интенсивности внеш. И., т. е. кол-ву резонансных фотонов. Существование вынужденного И. было постулировано Эйнштейном в 1916 при теор. анализе процессов теплового И. тел с позиций квант. теории и затем было подтверждено экспериментально. В обычных условиях интенсивность вынужденного И. мала по сравнению с интенсивностью спонтанного. Однако она сильно возрастает в т. н. активной среде, в к-рой искусственно создана инверсия населённостей, т. е. в одном из возбуждённых состояний находится больше атомов, чем в одном из состояний с меньшей энергией. При попадании в такую среду резонансного фотона испускаются фотоны, в свою очередь играющие роль резонансных. Число излучаемых фотонов лавинообразно возрастает; результирующее И. состоит из фотонов, идентичных по своим св-вам, т. е. образуется когерентный поток И. (см. КОГЕРЕНТНОСТЬ). На этом явлении основано действие квантовых генераторов и квантовых усилителей И.Значение теории излучения. Практич. и научно-прикладное значение теории И. огромно. На ней основываются разработка и применение лазеров и мазеров, создание новых источников света, ряд важных достижений в области радиотехники и спектроскопии. Понимание и изучение законов И. важно и в др. отношении: по хар-ру И. (энергетич. спектру, угл. распределению, поляризации) можно судить о св-вах излучателя. Эл.-магн. И.— пока фактически единственный и весьма многосторонний источник информации о косм. объектах. Напр., анализ И., приходящего из космоса, позволил открыть такие необычные небесные тела, как пульсары. Изучение спектров далёких внегалактич. объектов подтвердило теорию расширяющейся Вселенной. С другой стороны, исследование И. позволило решить мн. вопросы строения в-ва. Именно теории И. принадлежит особая роль в формировании всей совр. физ. картины мира: преодоление трудностей, возникших в электродинамике движущихся сред, привело к созданию относительности теории; исследования Планком теплового излучения положили начало всей квант. теории.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- ИЗЛУЧЕНИЕ
-
электромагнитное - 1) процесс образования свободного эл.-магн. поля при неравномерном движении и взаимодействии электрич. зарядов. 2) Свободное эл.-магн. поле (электромагнитные волны). Создаваемое произвольно движущимся электрич. зарядом эл.-магн. поле в общем случае является суммой как сосредоточенного вблизи заряда и движущегося вместе с ним собств. поля, так и уходящего от заряда на бесконечно далёкие расстояния поля И. (поля эл.-магн. волн).Для системы зарядов собств. поле и поле И. являются суммами соответствующих полей каждого заряда. Существование поля И. - следствие конечности величины скорости распространения эл.-магн. волн в вакууме: е=3.1010 см/с. Изменение движения заряда изменяет поле на расстоянии rот него только черезпромежуток времени r/с (поэтому, напр., при исчезновении зарядов в процессе аннигиляции электрона и позитрона поле И. продолжает существовать и после процесса аннигиляции). Существование поля после исчезновения источника означает, что эл.- магн. поле обладает энергией и импульсом. Удаление поля И. на бесконечно далёкие расстояния от источника сопровождается потоком уходящей от источника энергии. Образовавшееся в процессе И. эл.- магн. ноле уносит энергию от системы зарядов. Плотность потока энергии (кол-во энергии, протекающей за единицу времени через единицу нормальной к нему поверхности) определяется Пойнтинга вектором, пропорциональным векторному произведению [ ЕН] напряжённостей электрич. Е и магн. Н полей в эл.-магн. волне. На далёких от системы зарядов расстояниях её собств. поле пренебрежимо мало и вся энергия определяется полем И. Поток энергии поля И. через сферу большого радиуса r с центром внутри системы зарядов поэтому не должен зависеть от r:
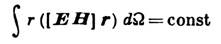
(W - телесный угол). Отсюда следует, что величины E и Н обратно пропорциональны r. Излучаемое поле в общем случае действует на источник И., совершая работу над токами в излучающей системе. Силы, действующие на систему со стороны излучаемогo поля, наз, силами реакции излучения или радиационными силами. Работа радиац. силы над источником складывается из потерь энергии на И. и из изменения энергии эл.- магн. поля, созданного системой. И. характеризует частота w (длина волны l=с/2pw) или набор частот, интенсивность его может зависеть от направления, т. е. энергия И. системы распределяется к.-л. образом по углам и частотам. Если законы движения r1(t), . . ., rN(t) каждого из N зарядов (е 1, . . ., eN) излучающей системы известны, то Максвелла уравнения позволяют получить энергию И. системы в интервале частот dwв элемент телесного угла dW, выбранного вокруг единичного вектора п, направленного на точку наблюдения: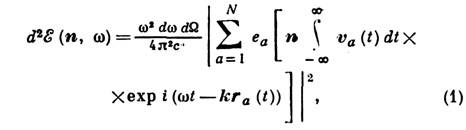
где va(t) = dra(t)/dt - скорость а-го заряда, k=n(w/c). Выражение (1) применимо в том случае, когда точка наблюдения бесконечно удалена от заряда, т. е. все характерные размеры задачи пренебрежимо малы по сравнению с расстоянием r до точки наблюдения. Излучение произвольно движущегося заряда. Распределение И. одного заряда, движущегося с ускорением, по частотам (частотный спектр И.) можно получить, интегрируя по углам выражение (1) при N=1: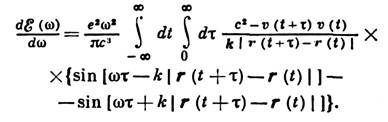
Для случая, когда заряд е равномерно движется со скоростью v и в момент времени t=0 мгновенно останавливается, получим: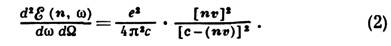
Приближение мгновенной остановки справедливо, если промежуток времени Dt, в течение к-рого заряд останавливается, мал по сравнению с эфф. промежуткомвремени, дающим осн. вклад в интеграл по времени в (1). Можно показать, что этот эфф. промежуток времени имеет величину ~(w-kv)-1, тогда условие применимости приближения мгновенной остановки имеет вид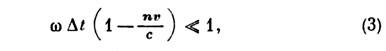
т. е. рассматриваемая область частот имеет верхнюю границу. Для ультрарелятивистских частиц и малых углов V между направлениями наблюдения И. и распространения частиц (в ультрарелятивистском случае существенны только малые углы) это неравенство примет вид: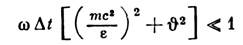
(e - энергия частиц). Из (2) следует, что распределение излучаемой энергии по частотам не зависит от частоты. Распределение излученной энергии по W и w также описывается ф-лой (2), если вместо внезапной остановки рассмотреть внезапное начало движения заряда с пост. скоростью; такая задача соответствует, в частности, излучению при бета-распаде ядра атома. Причины, вызывающие изменение движения заряж. частицы, могут быть различными. В зависимости от них возможны разл. типы И., к-рые имеют свои особенности. Тормозное излучение возникает при торможении и отклонении от нач. направления движения заряж. частицы в результате её рассеяния на атоме. Если время Dt, за к-рое заряд меняет скорость от v1 до v2, удовлетворяет условию (3), то отклонение можно считать мгновенным, тогда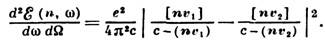
Умножив это выражение на вероятность изменения скорости частицы от v1 до v2 и проинтегрировав полученное выражение по всем v2, получим распределение энергии тормозного И. по углам и частотам (не зависящее от частоты). Тормозное И.- осн. причина потерь энергии релятивистских электронов в веществе, если энергия электрона больше нек-рой критической, составляющей для воздуха - 83, для Аl-47 и для Рb-59 МэВ. Магнитотормозное излучение возникает при движении заряж. частицы в магн. поле, искривляющем траекторию её движения. В постоянном и однородном магн. поле частица движется по окружности с частотой обращения W=ecH/e. (Н - напряжённость магн. поля, e - энергия заряж. частицы). Периодичность движения заряда приводит к тому, что излучаемые частоты - целые кратные частоты W; w=nW. При ультрарелятивистских энергиях заряда eдmс 2 наблюдается синхротронное излучение, обладающее широким спектром частот с максимумом в области частот ~W(e/тс 2)3, в т. ч. осн. доля энергии приходится на область частот wдW. В этой области интервалы между соседними частотами малы по сравнению с частотой со и распределение частот в спектре синхротронного И. можно считать непрерывным. В области частот wЪW (e/тс 2)3 излучаемая энергия растёт с частотой как w2/3, в области wдW(e/тс 2)3 - экспоненциально убывает с ростом частоты. Синхротронное И. обладает также малой угл. расходимостью (~ тс 2/e) и высокой степенью поляризации в плоскости орбиты. Эти свойства синхротронного И., а также возможность точного вычисления его свойств привели к широкому использованию синхротронного И. для спектроскопии в области от рентгеновского до видимого диапазона длин волн (рентгеновская спектроскопия тонкой структуры протяжённого поглощения - EXAFS, фотоэлектронная спектроскопия, спектроскопия высокого разрешения и др.). Магнитотормозное И. при нерелятивистских скоростях заряда получило назв. циклотронного И. Оно обладает общими свойствами И. нерелятивистских частиц -дипольного И. (см. ниже). Его частота совпадает с частотой обращения заряда по окружности W. Ондуляторное И. возникает при движении ультрарелятивистской заряж. частицы с малыми поперечными периодич. отклонениями, возникающими, напр., при ее пролёте через конденсатор с переменным во времени электрич. полем Е=Е 0cosw0t, перпендикулярным к направлению ср. скорости частицы v (см. Ондуляторное излучение). Частота ондуляторного И. связана с частотой поперечных колебаний w0 соотношением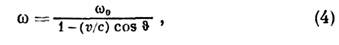
где V - угол между v и направлением наблюдения; т. о., частота ондуляторного И. жёстко связана с углом наблюдения И. Аналогом ондуляторного И. является И. при каналировании заряженных частиц в монокристалле, при к-ром прямолинейно движущаяся между соседними кристаллографич. плоскостями частица испытывает поперечные колебания в результате взаимодействия с внутрикристаллич. полем. Излучение Черенкова - Вавилова возникает при равномерном движении заряда в среде со скоростью, превышающей фазовую скорость света с/ Цe в этой среде (здесь e - диэлектрическая проницаемость среды). Распределение излучаемой энергии по углам и частотам для системы зарядов в среде отличается от (1) множителем Цe и др. определением k:k=(w/c)nЦe.Для равномерно движущегося единичного заряда распределение интенсивности излучения Черенкова - Вавилова имеет вид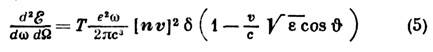
( Т - полное время наблюдения). Появление в этом выражении дельта-функции d[1-(v/с)Ц(e).cosV] означает, что Vопределяется равенством cosV=(c/v) Цe. Излучение Черенкова - Вавилова используется для измерения энергии заряж. частиц. Переходное излучение возникает при пересечении равномерно движущимся зарядом области пространства с неоднородными диэлектрич. свойствами, напр., при пересечении им границы раздела двух сред с разл. диэлектрич. проницаемостями или при движении в среде, содержащей неоднородности. Переходное И. и излучение Черенкова - Вавилова - родственные явления, т. к. и то и другое - испускание эл.- магн. волн атомами вещества, возбуждёнными движущейся частицей: Черенкова - Вавилова И.- результат когерентного высвечивания возбуждённых частицей атомов, а переходное - некогерентного высвечивания этих атомов. Когерентность различных излучателей. Пусть N идентичных излучателей, в каждом из к-рых электрич. заряд движется по одному и тому же закону r0(t), имеют разл. нач. координаты Ra и разл. нач. моменты времени ta. В момент времени t координаты а-го излучателя имеют видra(t)=Ra + r0(t-ta).
Подставляя это выражение в (1), можно выразить распределение излучаемой всеми N излучателями энергии d2EN(n, w) через энергию, излучаемую отд. излучателем:
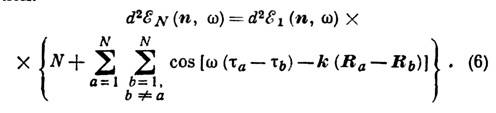
Если, напр., аргумент косинуса близок к нулю для любых а и b, то излучаемая системой энергия пропорц. квадрату числа излучателей: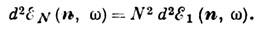
Это означает, что в точку наблюдения эл.-магн. волны от разных излучателей приходят с одинаковыми фазами и поля арифметически складываются. Такие излучатели наз. когерентными по отношению друг к другу. В том случае, когда R а или t а - случайные величины, излучаемая энергия должна быть усреднена по их распределению. При таком усреднении излучаемая энергия становится пропорциональной числу излучателей:d2EN(n, w) =Nd2E1(n, w).
Эл.-магн. волны от разных излучателей приходят в точку наблюдения с самыми различными фазами и взаимно погашаются; эффективно складываются потоки энергии, созданные разл. излучателями. Такие излучатели наз. взаимно некогерентными. В обычных источниках света (напр., пламени) высвечивание атомов происходит за счёт хим. экзотермич. реакции. В этом случае моменты времени, в к-рые происходит возбуждение разл. атомов, распределены случайным образом, следовательно, нач. моменты t а - случайны. Такие источники И. некогерентны. Некогерентными источниками И. являются также излучающие атомы металла в лампах накаливания, атомы газа в люминесцентных лампах и т. д. При движении частицы в среде со скоростью v нач. моменты t0 движения заряда в излучателях определяются временем подлёта частицы к атому. Поэтому для лежащих вблизи пути частицы атомов R а-Rь=v(ta-tb). Выражение (6) в этом случае примет вид:
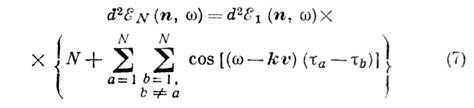
При выполнении условия w=kv, т. е. cosV=( с/v) Цe, получим:d2EN(n,w)=N2d2E1(n, w).
Т. о., все расположенные вблизи пути частицы атомы будут излучать когерентно. Это и происходит в случае излучения Черенкова - Вавилова. Во всех др. направлениях, для к-рых cosV№( с/v) Цe, возбуждённые атомы излучают некогерентно. То же самое происходит при скорости частицы v<c/ Цe. В однородном веществе И. разных излучателей полностью погашается. Если в веществе присутствуют микроскопич. неоднородности, то полного погашения волн от разных излучателей в точке наблюдения не происходит. Наличие поверхности раздела двух сред препятствует взаимному погашению полей в точке наблюдения от излучателей, находящихся по разным сторонам поверхности раздела и увеличивает интенсивность некогерентного высвечивания возбуждённых атомов, т. е. переходного И. Дипольное излучение системы нерелятивистских зарядов. Рассмотрим систему зарядов, движущихся с нерелятивистскими скоростями порядка г; внутри области пространства размером a. Период колебания заряда в такой системе ~а/v, а частота ~v/a. Отсюда следует v/w~a Ъl~c/w, так что kr а~a/l Ъ1 и в (1) член с kra в показателе экспоненты можно опустить:
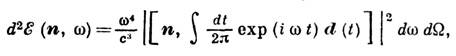
где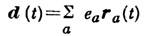 - представляет собой дипольныймомент системы зарядов. Распределение по углам и частотам энергии, излучаемой системой нерелятивистских зарядов, полностью определяется дипольным моментом системы зарядов; такое И. наз. дипольным. Для дипольного И. характерно угл. распределение, пропорциональное sin2V. Наиб. энергия излучается под
- представляет собой дипольныймомент системы зарядов. Распределение по углам и частотам энергии, излучаемой системой нерелятивистских зарядов, полностью определяется дипольным моментом системы зарядов; такое И. наз. дипольным. Для дипольного И. характерно угл. распределение, пропорциональное sin2V. Наиб. энергия излучается подпрямым углом к направлению дипольного момента, в направлении же дипольного момента И. отсутствует. Интегрирование по углам даёт спектр дипольного И.:
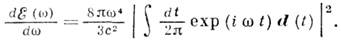
Условие применимости дипольного приближения можно записать и как w Ъ с/а, что ограничивает рост интенсивности дипольного И. с частотой. Циклотронное И. заряда, движущегося с нерелятивистской скоростью в постоянном и однородном магн. поле, является частным случаем дипольного И. При таком движении частота И. w равна частоте W обращения заряда по окружности. Если дипольный момент системы нерелятивистских зарядов равен нулю, то следует учесть линейные члены разложения (1) по степеням kr. В этом приближении И. системы определяется её магн. дипольным моментом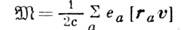
и электрич. квадрупольным моментом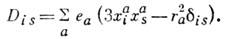
Дипольный момент системы, в частности, равен нулю для системы с одинаковым отношением заряда к массе для всех частиц. У такой системы исчезает и магн. момент, так что её И. будет квадрупольным. Если магн. дипольный и электрич. квадрупольный моменты равны нулю, то И. определяется мультиполями более высоких порядков (n>2; для дипольного момента n=1). В создаваемое системой зарядов и токов И. вносят вклад также анапольные моменты (см. Анаполъ), однако в распределение энергии они вносят вклад не независимо, а в виде определ. комбинации с электрич. мультипольным моментом (см., напр., Квадрупольное излучение). Приведённые ф-лы справедливы для И. как микроскопической, так и макроскопич. систем (напр., для И. Герца вибратора). Об И. радиоволн см. в ст. Антенна.
Квантовая теория излучения. Процесс И. квантовой системы (атома, атомного ядра, молекулы) подчиняется квантовым законам (см. Квантовая электродинамика). В квантовой теории И. эл.-магн. поле рассматривается как совокупность квантов эл.-магн. поля - фотонов. Энергия фотона е пропорц. его частоте: e=hw, импульс р - его волновому вектору k: p=hk. И. одного фотона квантовой системой сопровождается переходом этой системы из состояния с энергией E1 в состояние с энергией E2=E1-hw. Т. к. энергия квантовой системы дискретна, такая система испускает И. определ. частот - спектр И., состоящий из отд. спектральных линий с конечной шириной.
Дипольное излучение атома. Длина волны lИ. атома значительно превышает его радиус а,l дa, т. е. выполняется условие применимости дипольного приближения. Наиб, интенсивные линии в атомных спектрах получаются в результате днпольных электрич. переходов. Роль классич. плотности тока при таком рассмотрении играет ток перехода, т. е. матричный элемент оператора плотности тока, вычисленный с волновыми ф-циями нач. и конечного состояний атома. В дипольном приближении матричный элемент оператора плотности тока сводится к матричному элементу оператора дипольного момента системы. Т. к. дипольный момент является вектором, его матричные элементы между состояниями с квантовыми числами n, l, т, s и п', I', m', s' не обращаются в нуль только при выполнении определ. равенств, наз. отбора правилами:l'-l=b1,0m' - m = b1,0(кроме случая, когда и l=0и l'=0).
Мультипольное излучение атома. Представление энергии И. квантовой системы в виде ряда, соответствующего И. мультипольных моментов разл. порядка, применимо лишь в том случае, когда l дa, а скорости электронов атома нерелятивистские. Тогда интенсивность И. мультиполя порядка (n+1) меньше интенсивности И. мультиполя порядка п в (l/a)2 раз. Для того чтобы матричный элемент соответствующего мультипольного момента был не равен нулю, необходимо выполнение определ. правил отбора, вытекающих из законов сохранения момента и чётности. Если L - момент кол-ва движения фотона, М - его проекция, j1, j2 и m1,m2 - моменты кол-ва движения и проекции момента электрона в нач. и конечном состояниях, то действуют след. правила отбора:m1- m2=М,|j1- j2|[L[|j1+ j2|P1=P2P,
где P1 п Р 2 - чётности нач. и конечных состояний электрона, Р= (-1)L+i+d(d=0 соответствует состояниям магнитного, а d=1 - состояниям электрич. типа). Если правила отбора не выполняются, то И. соответствующей мультипольности отсутствует. Время жизни атома в возбуждённом состоянии по отношению к диполышму И. обычно ~10-8 с. Если из возбуждённого состояния дипольное И. невозможно (не выполняются правила отбора), а возможно только мультипольное И. порядка п, то время жизни такого состояния увеличивается в (l/а)2(n-1) раз. Такие состояния наз. метастабильными.
Мультипольное излучение ядер. Если для атомных электронов их скорости удовлетворяют соотношениям v~аw~с/137, то для нуклонов в ядре величины а, w и v не находятся в к.-л. определ. соотношениях. Поэтому для атомных ядер применение разложения по мультиполям возможно только при выполнении двух неравенств:v Ъ с и а Ъl.Возбуждённые метастабильные состояния ядер, для к-рых И. возможно лишь при L~3-5, обладают временами жизни порядка минут и часов; о ядрах в таких состояниях см. в ст. Ядерная изомерия.
Вынужденное излучение. Вероятность И. фотона с импульсом p= hk и энергией e= hw пропорц. (nk+1), где nk - число точно таких же фотонов, находившихся в системе до момента И. При nk=0 И. наз. спонтанным. Пропорциональная nk часть И. наз. вынужденным испусканием. В квантовых генераторах, И. к-рых является вынужденным, для увеличения nk используются резонаторы, удерживающие поле вблизи излучателя. Каждый испущенный веществом фотон увеличивает nk, и интенсивность И. с данным k быстро растёт при малой интенсивности И. всех фотонов др. частот. В результате энергия излучателя оказывается сосредоточенной в очень узкой полосе частот со, причём все фотоны испускаются в одном направлении. Поля И. на этой частоте имеют большую величину, сравнимую с величиной внутримолекулярных полей, в результате чего прохождение такого ноля в среде меняет её свойства, т. к. взаимодействие поля И. с веществом становится нелинейным (см. Нелинейная оптика). Лит.: Ландау Л. Д., Лифшиц Е. М., Теория поля, 7 изд., М., 1988; их же, Электродинамика сплошных сред, 2 изд., М., 1982; А х и е з е р А. И., Берестецкий В. Б., Квантовая электродинамика, 4 изд., М., 1981; Джексон Д ж.. Классическая электродинамика, пер. с англ., М.. 1965. М. И. Рязанов.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.