Akademik

- наука о наиболее общих тепловых свойствах макроскопич. тел. Термодинамич. подход не требует привлечения упрощённых моделей рассматриваемых явлений, поэтому выводы Т. имеют универсальный характер.

История развития термодинамики. Зарождение Т. как науки связано с именем Г. Галилея (G. Galilei), к-рый ввёл понятие температуры и сконструировал первый прибор, реагирующий на изменения темп-ры окружающей среды (1597). К. Ренальдини (С. Renaldini) предложил градуировать термометр по реперным точкам. Г. Д. Фаренгейт (G. D. Fahrenheit, 1714), Р. Реомюр (R. Reaumur, 1730} и А. Цельсий (A. Celsius, 1742) создали температурные шкалы в соответствии с этим принципом. В результате работ Г. В. Рихмана (1744) формируется понятие теплоты.

Дж. Блэк (J. Black) ввёл понятия скрытой теплоты плавления (1757) и теплоемкости (1770), И, Вильке (J. Wilcke, 1772) ввёл определение калории как кол-ва тепла, необходимого для нагревания 1 г воды на 1 °С. А. Лавуазье (A. Lavoisier) и П. Лаплас (P. Laplace) в 1780 сконструировали калориметр (см. Калориметрия )и впервые экспериментально определили уд. теплоёмкости ряда веществ. В 1824 С. Карно (N. L, S. Carnot) опубликовал работу, посвящённую исследованию принципов работы тепловых двигателей. Б. Клапейрон (В. Clapeyron) ввёл графич. представление термодинамич. процессов и развил метод бесконечно малых циклов (1834), Ю. Р. Майер (J. R. Мауег) сформулировал принцип взаимопревращае-мости теплового и механич. движений и теоретически вычислил термомеханич. эквивалент (1842), экспериментально его определил Дж. П, Джоуль (J. P. Joule, 1843), Г. Хельмгольц (G. Helmholtz) отметил универсальный характер закона сохранения энергии (1847). Впоследствии Р. Клаузиус (R. Clausius) и У. Томсон (Кельвин; W. Thomson) систематически развили теоретич. аппарат Т., в основу к-рого положены первое начало термодинамики и второе начало термодинамики. Развитие 2-го начала привело Клаузиуса к определению энтропии (1854) и формулировке закона возрастания энтропии (1865). Ста-тистич. интерпретация энтропии была дана Л. Больцма-ном (L. Boltzmann, 1872). Начиная с работ Дж. У. Гиббса (J. W. Gibbs, 1873), предложившего метод термодинамических потенциалов, развивается теория термодинамич. равновесия. Во 2-й пол. 19 в. проводились исследования Т. реальных газов. Особую роль сыграли эксперименты Т. Эндрюса (Т. Andrews), к-рый впервые обнаружил критическую точку системы жидкость-пар (1861), её существование предсказал Д. И. Менделеев (1860). К кон. 19 в. были достигнуты большие успехи в получении низких температур, в результате чего были ожижены О ₂, N₂ и Н ₂, а затем и Не. Эксперим. исследования в области низких темп-р позволили В. Нернсту (W; Nernst) сформулировать третье начало термодинамики(1906). В 1902 Гиббс опубликовал работу, в к-рой все осн. термодинамич. соотношения были получены в рамках статистической физики. Связь между кинетич. свойствами тела и его термодинамич. характеристиками была установлена Л. Онсагером (L. Onsager, 1931). В 20 в. интенсивно исследовали Т. твёрдых тел, а также квантовых жидкостей и жидких кристаллов, в к-рых имеют место многообразные фазовые переходы. Л. Д. Ландау (1935-37) развил общую теорию фазовых переходов, основанную на концепции спонтанного нарушения симметрии.

Основные понятия термодинамики. В Т. изучают мак-роскопич. системы, т. е. системы, состоящие из большого числа частиц, причём исследуют наиб. общие свойства таких систем, для описания к-рых не требуется привлечения микроскопич. характеристик системы. Термодинамич. подход оказывается тем точнее, чем больше частиц в системе. З а м к н у т о й с и с т е м о й наз. система, изолированная от к.-л. внеш. воздействия, такую систему всегда можно разбить на составляющие её подсистемы, слабо взаимодействующие между собой. Телом в Т. наз. макроскопич. систему, заключённую в определ. объём.

Равновесным состоянием наз. состояние макроскопич. системы, в к-ром отсутствуют потоки (массы, заряда, энергии, импульса и т. п.) между её подсистемами. Замкнутая система по истечении достаточно большого промежутка времени всегда приходит в равновесное состояние. Равновесное состояние макроскопич. системы однозначно определяется неск. термодинамическими параметрами (см. Параметры состояния). Так, равновесное состояние жидкости или газа (с фиксированным числом частиц) можно задать двумя параметрами, напр. давлением P и объёмом V. В более сложных системах число термодинамич. параметров увеличивается. Напр., в смеси газов или жидком растворе в их число необходимо включить концентрации отд. компонентов, состояние твёрдого тела следует описывать тензором деформации. При рассмотрении эл.-магн. явлений термодинамич. систему характеризуют такими параметрами, как заряд, поляризация среды, магн. момент. Для систем с нарушенной симметрией в число термодинамич. параметров включают параметр порядка.

Темп-pa является количеств. характеристикой теплового равновесия: темп-ры тел, находящихся в равновесии друг с другом, равны между собой. На этом основано измерение темп-ры при помощи термометра. В качестве термометра можно взять любое тело, термодинамич. параметры к-рого зависят от темп-ры. Определение температурной шкалы не однозначно и зависит от способа градуировки термометра. Общепринятой является Кельвина шкала темп-ры, в соответствии с к-рой темп-pa Т измеряется в градусах Кельвина. При взаимодействии двух тел, имеющих разл. темп-ру, происходит процесс установления равновесия между ними, сопровождающийся теплопередачей. При этом кол-во теплоты, отданное одним телом, равно кол-ву теплоты, приобретённому другим. На этом основано количеств. измерение переданной теплоты при помощи калориметра, к-рый служит источником или стоком тепла. В качестве калориметра можно использовать любое тело, термодинамич. параметры к-рого зависят от кол-ва переданной ему теплоты.

П р о ц е с с о м в Т. наз. изменение состояния тела со временем. Важными характеристиками процесса являются поглощённое телом кол-во теплоты Q, а также совершённая над ним работа А. Обе эти величины существенно зависят от хода процесса. Обратимым процессом наз. процесс, достаточно медленный для того, чтобы состояние тела в каждый момент времени можно было считать равновесным. Равновесное состояние тела изображается точкой в пространстве его термодинамич. параметров, так что обратимый процесс изображается нек-рой кривой в этом пространстве. Для описания обратимого процесса используют ряд дифференц. характеристик, в качестве к-рых выбирают след. производные вдоль упомянутой кривой: т е п л о ё м к о с т ь

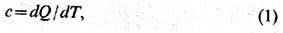
к о э ф. т е п л о в о г о р а с ш и р е н и я

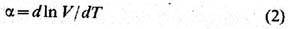
и к о э ф. с ж и м а е м о с т и

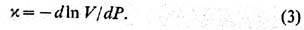
Работа, совершаемая над телом в ходе процесса, может быть механической или иметь др. природу. Работа сил давления для бесконечно малого изменения состояния тела равна

dA=-PdV.(4)

Начала термодинамики. Три начала Т. являются основой, на к-рой строится её теоретич. аппарат. Эти начала являются эксперим. фактами, прошедшими продолжит. и всестороннюю проверку. Теоретич. обоснование этим фактам даёт раздел Статистическое истолкование термодинамики в ст. Статистическая физика,

П е р в о е н а ч а л о т е р м о д и н а м и к и утверждает, что поглощённое телом кол-во теплоты Q является, наряду с совершённой над ним работой А, мерой изменения его внутренней энергии U. Т. о., для бесконечно малого изменения состояния тела

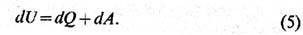
Это равенство является выражением закона сохранения энергии для термодинамич. систем. Внутр. энергия тела U является ф-цией его состояния, это аддитивная величина, т. е. для любой макроскопич. системы она равна сумме внутр. энергий составляющих её подсистем. Соотношение (5) показывает, что кол-во теплоты Q измеряется в энерге-тич. единицах. 1-е начало Т. эквивалентно утверждению о невозможности создания вечного двигателя 1-го рода, т. е. устройства, способного совершать работу без потребления энергии.

Помимо внутр. энергии U любая термодинамич. система характеризуется ещё одной аддитивной ф-цией состояния - энтропией S, изменение к-рой при бесконечно малом обратимом процессе связано с поглощённой системой теплотой:

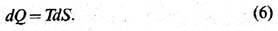
Здесь Т-абсолютная температура. Выражение (6) указывает путь эксперим. построения абс. шкалы темп-р; величина Т должна быть такой, чтобы интеграл

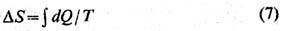
не зависел от способа перехода из нач. состояния в конечное. Утверждение о возможности такого построения наз. иногда 2-м началом Т. для обратимых процессов. Абс. темп-pa Т является положительно определённой величиной. (Понятие отрицательной температуры вводится для сильно неравновесных подсистем.) Фиксируя в интеграле (7) нач. точку процесса и изменяя конечную, можно вычислить (с точностью до константы) энтропию S для любого равновесного состояния системы. Для определения энтропии S неравновесной системы следует воспользоваться аддитивностью энтропии, т. е. вычислять S как сумму энтропии подсистем, достаточно малых для того, чтобы считать их внутр. состояния равновесными.

В т о р о е н а ч а л о т е р м о д и н а м и к и свидетельствует о необратимости термодинамич. процессов. При соприкосновении двух тел теплота самопроизвольно переходит от более нагретого тела, т. е. тела с большей абс. темп-рой, к менее нагретому телу, т. е. телу с меньшей абс. темп-рой. Для того чтобы передать теплоту от менее нагретого тела к более нагретому, необходимо совершить работу (такой процесс осуществляется в холодильных машинах). 2-е начало Т. можно сформулировать в виде утверждения о невозможности создания вечного двигателя 2-го рода, т. е. устройства, полностью преобразующего тепловую энергию к.-л. тела в работу. Количеств. выражением необратимости термодинамич. процессов является закон возрастания энтропии: энтропия замкнутой системы возрастает (точнее, не убывает) со временем.

1-е и 2-е начала Т. используют, в частности, для исследования закономерностей функционирования тепловых машин. Эффективность тепловой машины характеризуется коэф. полезного действия (кпд), равным отношению работы, совершённой тепловой машиной, к теплоте, потерянной нагревателем. Из соотношений (5) и (6) следует, что кпд тепловой машины, рабочее тело к-рой совершает обратимый Карно цикл, равен

здесь T₁. -абс. темп-pa нагревателя, Т₂- абс. темп-ра холодильника. Из 2-го начала Т. следует Карно теорема, согласно к-рой кпд любой тепловой машины не может превосходить (8), где T₁ -макс., Т₂.- мин. абс. темп-ры рабочего тела.

Свойства термодинамич. систем вблизи нуля абс. темп-ры устанавливает т р е т ь е н а ч а л о т е р м о д и н а м и к и, согласно к-рому энтропия любой равновесной системы стремится к 0, если Т0. 3-е начало Т. устанавливает начало отсчёта энтропии, что однозначно фиксирует её для любой системы. Из 3-го начала, в частности, следует, что при Т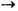0 обращается в 0 коэф. теплового расширения тела, а также теплоёмкость для любого процесса. Последнее позволяет дать альтернативную формулировку 3-му началу Т., согласно к-рой абс. нуль темп-ры экспериментально недостижим. Энтропия стёкол и др. неупорядоченных систем не стремится к нулю при охлаждении, т. к. эти системы метастабильны, т. е. не являются в строгом смысле равновесными.

Термодинамические потенциалы. Метод термодинамич. потенциалов используют для описания обратимых процессов. В простейшем случае равновесное состояние тела можно описать двумя параметрами, при этом можно ограничиться выражением (4) для совершённой над телом работы. Из соотношений (5) и (6) получаем след. выражение для дифференциала внутр. энергии:

С помощью Лежандра преобразований можно перейти от внутр. энергии U к Гельмгольца энергии (свободной энергии) F, Гиббca энергии G и энтальпии Н. Соответств. диф-ференц. соотношения имеют след. вид:

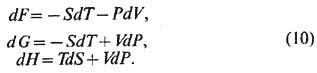
Термодинамич. потенциалами наз. введённые выше величины U(S, F), F(T, F), G(T, P), H(S, P). Если известна любая из этих ф-ций, то на основании соответств. термодинамич. тождеств (9), (10) можно определить все термодинамич. характеристики системы. Так, прямым дифференцированием F(T, V )можно найти ф-ции S = S(T, V), P =P (Т, V). Функциональная зависимость P от Т и V наз. уравнением состояния. Зная ур-ние состояния, можно в соответствии с определениями (2), (3) найти изобарич. козф. теплового расширения тела

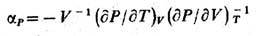
и изотермич. сжимаемость

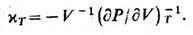
Дифференцируя ф-цию S, можно в соответствии с (1), (6) найти изохорич. теплоёмкость тела

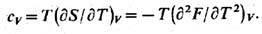
Аналогично вычисляют изобарич. теплоёмкость

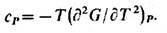
При переходе в дифференц. соотношениях от одного набора термодинамич. переменных к другому удобно использовать технику якобианов. Для двух пар переменных ( а, b) ( х, у) якобиан равен

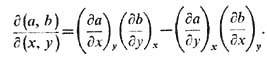
Справедливы след. тождества:

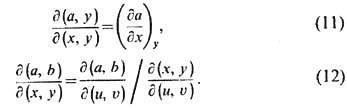
Соотношение (11) позволяет записывать введённые выше величины через якобианы, а соотношение (12) позволяет выражать эти величины через производные по любой паре термодинамич. переменных. Так, для изобарич. теплоёмкости с _Р=Тд(S, Р)/д(Т, Р). Переходя в этом выражении от переменных Т, P кпеременным Т, V по ф-ле (12) и используя соотношение между вторыми производными свободной энергии ( дP/дT)_V = (дS/дV)_T , можно получить:

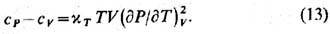
Аналогично выводится связь между изотермич. и адиаба-тич. сжимаемостями:

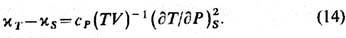
При помощи якобианов легко показать, что

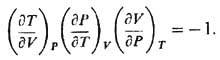
Аналогичное соотношение имеет место для любой тройки переменных, связанных функциональной зависимостью.

В более общей ситуации равновесное состояние тела описывается произвольным числом термодинамич. параметров. Э к с т е н с и в н ы м и (аддитивными) параметрами наз. величины, к-рые при разбиении системы на подсистемы разбиваются на сумму по подсистемам. И н т е н с и в н ы м и переменными наз. величины, не зависящие от этого разбиения, Тёрмодинамич, параметры любой системы можно представить в виде совокупности термодинамически сопряжённых экстенсивных и интенсивных переменных. Выше были рассмотрены пары (S, Т )и (V, Р). Ещё одна пара термодинамически сопряжённых переменных возникает при рассмотрении систем с перем. числом частиц: (N, m), где N- число частиц, а m - химический потенциал:

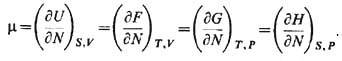
Совершая преобразование Лежандра по N,m над свободной энергией F, приходим к термодинамич. потенциалу W, дифференциал к-рого имеет след. вид:

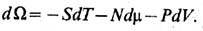
Термодинамич. потенциал W непосредственно выражается через давление и объём: W= - PV. Др. примерами термодинамически сопряжённых пар экстенсивных и интенсивных переменных являются электрич. поляризация и элек-трич. поле, магн. момент и магн. поле, электрич. заряд и электрич. потенциал. Обозначив совокупность всех дополнит. пар термодинамически сопряжённых переменных ( Х _а, Y_a ), придём к след. обобщению термодинамич. тождеств (9), (10):

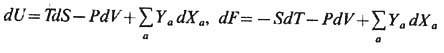
и т. д.

Обобщённой восприимчивостью наз. матрица

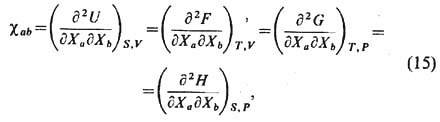
для к-рой справедливы соотношения

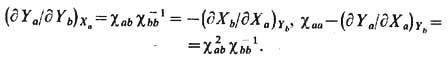
Последнее равенство является обобщением соотношений (13), (14),

Из определения (15) следует, что матрица обобщённой восприимчивости c_ab симметрична, т. е. дY _а/дХ _b = = дY_b/дХ _а. Эти равенства (наряду с аналогичными равенствами дT/дX_a = дY _а/дS и дP/дX_a = дY_a/дV )приводят к нетривиальным эксперим. следствиям.

Термодинамическое равновесие. Теория термодинамич. равновесия исследует общие условия равновесия подсистем, а также условия устойчивости термодинамич. равновесия. Исследование этих условий основано на законе возрастания энтропии, вследствие к-рого энтропия замкнутой системы достигает в равновесии своего максимума.

Пусть тело взаимодействует с т е р м о с т а т о м (настолько большой системой, что можно пренебречь изменением её интенсивных параметров при взаимодействии с исследуемым телом). Условие максимальности энтропии системы тело + термостат эквивалентно условию минимальности след. величины:

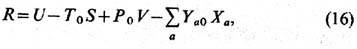
индекс 0 относится к интенсивным параметрам термостата, величины без индекса относятся к телу. Смысл последнего слагаемого в (16) заключается в том, что из-за взаимодействия с термостатом на тело накладывается внеш. поле.

Условиями экстремума R относительно вариаций (S, V )являются равенства

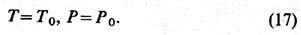
Т. о., взаимодействие с термостатом фиксирует абс. темп-ру и давление тела. Аналогично можно показать, что равенства абс. темп-р и давлений являются условиями равновесия (теплового и механич.) любых тел. Условия экстремума R относительно вариаций Х _а таковы:

При выводе условий равновесия (17), (18) предполагалось, что тело и термостат разделены подвижной стенкой, через к-рую они могут обмениваться теплотой, а также величинами Х _а. Тело можно поместить в адиабатич. и (или) изохорич. условия, фиксирующие энтропию S и объём V тела. В этом случае S и (или) V являются свободными параметрами. Не следует минимизировать R также по тем величинам Х _а, к-рыми тело не может обмениваться с термостатом (напр., по числу частиц N, если невозможен обмен частицами между телом и термостатом). При условиях (17) минимальность R относительно вариаций Х _а эквивалентна минимальности след. величины:

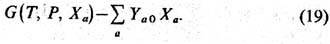
Если внеш. условия фиксируют др. термодинамич. параметры тела, то вместо G в (19) следует использовать со-ответств. термодинамич. потенциал, являющийся ф-цией этих фиксированных переменных.

Условие положит. определённости R относительно малых вариаций S и V приводит к неравенствам

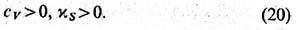
Неравенства (20) выражают условия устойчивости теплового и механич. равновесия. Положительно определёнными являются также величины С _Р и 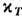. Кроме того, из соотношений (13), (14) следует c_p>c_V, 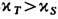. Условие минимальности R относительно малых вариаций Х _а эквивалентно условию положит. определённости квадратичной формы

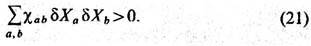
В общем случае в число dX_a следует включить dS и dV. Из (21) следует, в частности, что c _аа>0. Эти неравенства можно рассматривать как обобщение условий (20).

Примером может служить условие равновесия многокомпонентной системы относительно нек-рой хим. реакции. Изменение числа частиц компонентов в ходе этой реакции равно dN_i = v_idX, здесь индекс г нумерует компоненты, а v_i - численные коэф., фигурирующие в сим-волич. записи хим. реакции. Условие экстремальности величины R (в к-рой можно положить Y₀ = 0) относительно вариаций X таково: 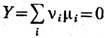, где m_i - хим. потенциалы компонент. Аналогично можно рассмотреть условия фазового равновесия. Так, условием равновесия двух фаз является равенство их хим. потенциалов. Это условие выделяет на плоскости ( Р, Т )кривую фазового равновесия P (Т), для к-рой справедливо Клапейрона - Клаузиуса уравнение. Граница раздела двух сосуществующих фаз характеризуется поверхностной энергией. Вне кривой фазового равновесия стабильной является фаза, обладающая мин. энергией Гиббса Ф. При определ. условиях в системе может реализоваться фаза, не обладающая мин. термодинамич. потенциалом, такое состояние системы наз. метастабиль-ным состоянием. Для его реализации необходима устойчивость метастабильной фазы относительно малых изменений всех возможных параметров Х _а, т. е. необходимо выполнение условия (21). Последнее нарушается в точке абс. неустойчивости метастабильной фазы.

Релаксацию неравновесного состояния системы к равновесному рассматривают в термодинамике неравновесных процессов.

Лит.: Фаулер Р., Гуггенгейм Э., Статистическая термодинамика, пер. с англ., М., 1949; Ландау Л. Д., Лифшиц E. М., Статистическая физика, 3 изд., ч. 1, М., 1976; Зоммерфельд А., Термодинамика и статистическая физика, пер. с нем., М., 1955; Хаар Д., Вергеланд Г., Элементарная термодинамика, пер, с англ., М., 1968; Кубо Р., Термодинамика, пер. с англ., М., 1970; Сивухин Д. В., Общий курс физики, 2 изд., [т. 2]-Термодинамика и молекулярная физика, М., 1979; Гиббс Дж. В., Термодинамика. Статистическая механика, пер, с англ., М., 1982; Леон-тович М. А., Введение в термодинамику. Статистическая физика, М., 1983. В, В. Лебедев, И, М. Халатников.