Akademik

РАБОТА

РАБОТА: силы, мера действия силы, зависящая от численной величины и направления силы и от перемещения точки её приложения. Если сила F численно и по направлению постоянна, а перемещение М0М1 прямолинейно (рис. 1), то P. A = F•s•cosa, где s=M0M1, a — угол между направлениями силы и перемещения. Когда a90°, Р. силы положительна, при 180°?a>90° — отрицательна, а при a=90°, т. е. когда сила перпендикулярна перемещению, А=0. Единицы измерения Р.: джоуль (в СИ), 1 эрг=10-7 Дж и килограмм-сила на метр (1 кгс•м=9,81 Дж).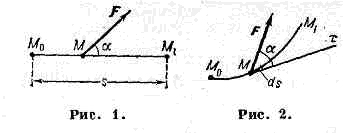

В общем случае для вычисления Р. силы вводится понятие элементарной работы dA=Fdscosa, где ds — элем. перемещение, a — угол между направлениями силы и касательной к траектории точки её приложения, направленной в сторону перемещения (рис. 2). В декартовых координатах

dA=Fxdx+Fydy+Fzdz, (1)

где Fx, Fy, Fz — проекции силы на координатные оси, х, у, z — координаты точки её приложения.

В обобщённых координатах

dA=SQidqi. (2)

где qi — обобщённые координаты, Qi — обобщённые силы. Для сил, действующих на тело, имеющее неподвижную ось вращения, dA=Mzdj, где Mz — сумма моментов сил относительно оси вращения z, j — угол поворота. Для сил давления dA=pdV, где р — давление, V — объём.

Р. силы на конечном перемещении определяется как интегральная сумма элементарных Р. и при перемещении М0М1 выражается криволинейным интегралом:

A=?M0M1)(Fcosa)ds или

A=?M0M1(Fxdx + Fydy + Fzdz). (3)

Для потенциальных сил dA=-dП и А= П0-П1, где П0 и П1 — значения потенциальной энергии П в нач. и конечном положениях системы; в этом случае Р. не зависит от вида траекторий точек приложения сил. При движении механич. системы сумма работ всех действующих сил на нек-ром перемещении равна изменению её кинетической энергии Т, т. е. SАi=T1-T0. Понятие «Р. силы» широко используется в механике, а также в др. областях физики и в технике.

Р. в термодинамике — обобщение понятия «Р. в механике» (выраженного в дифф. форме (2)). Обобщённые координаты в термодинамике -это внеш. параметры термодинамич. системы (объём, напряжённость внеш. магн. или электрич. поля и т. п.), а обобщённые силы (давление и др.) — величины, зависящие не только от координат, но и от внутр. параметров системы (темп-ры или энтропии). Р. термодинамич. системы над внеш. телами заключается в изменении состояния этих тел и определяется кол-вом энергии, передаваемой системой внеш. телам при изменении внеш. параметров системы. В квазистатических (т. е. бесконечно медленных) адиабатических процессах Р. равна изменению внутренней энергии системы, в квазистатич. изотермических процессах — изменению Гельмгольца энергии. В ряде случаев Р. может быть выражена через др. потенциалы термодинамические. В общем случае величина Р. при переходе системы из нач. состояния в конечное зависит от способа (пути), каким осуществляется этот переход. Это означает, что бесконечно малая (элементарная) Р. системы не явл. полным дифференциалом к.-л. функции состояния системы; поэтому элем. Р. обозначают обычно не dA (как полный дифференциал), а dА. Зависимость Р. от пути приводит к тому, что для кругового процесса, когда система вновь возвращается в исходное состояние, Р. системы может оказаться не равной нулю, что используется во всех тепловых двигателях. Работа внеш. сил над системой dА=-dA, если энергия вз-ствия системы с внеш. телами не меняется в процессе совершения Р. Примерами Р. при изменении одного из внеш. параметров системы могут служить: Р. сил давления р при изменении объёма V системы dA=pdV, Р. сил поверхностного натяжения при изменении поверхности системы dA=-sdS (s — коэфф. поверхностного натяжения, dS — элемент поверхности); Р. намагничивания системы dA=-HdJ (H — напряжённость внеш. магн. поля, J — намагниченность в-ва) и т. д. Р. системы в неравновесном (необратимом) процессе всегда меньше, чем в равновесном.

РАБОТА

в термодинамике - способ обмена энергией между термодинамич. системой и окружающими телами при изменении внеш. параметров состояния, к-рые определяют положение границ раздела системы или её частей и взаимодействие с внеш. силовыми полями; кол-во энергии, передаваемое этим способом. Др. способом обмена энергией, связанным с изменением энтропии, является передача теплоты. Величина Р. максимальна для квазистатич. процессов (принцип максимальной работы), в этом случае выражение для P. dW, производимой системой при бесконечно малом изменении внеш. параметров dx= {dx_i}, записывают по аналогии с механикой в виде 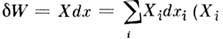- соответствующая параметру x_i обобщённая сила, характеризующая реакцию системы на квазистатич. изменение 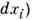Выражение для Р., совершаемой при конечном изменении состояния, записывают в виде интеграла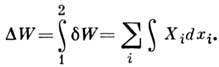

Это выражение существенно зависит от того, какие значения имеют величины 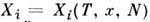в каждом из промежуточных состояний квазистатич. перехода 1 : 2, к-рые определяются не только набором параметров x_i, но и значениями темп-ры Т (или энтропии S) и чисел частиц отд. компонентов N = 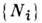. Величина DW зависит от пути интегрирования, а 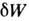не является полным дифференциалом в переменных ( Т, x, N), определяющих термодинамич. состояние системы. Поэтому в результате замкнутого кругового процесса можно получить отличную от нуля работу.

Величина 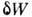участвует наряду с изменением внутр. энергии dU и величиной подводимого к системе тепла.

dQ в балансе, выражающем первое и второе начала термодинамики для квазистатич. процессов:

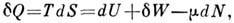
где 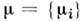- хим. потенциалы компонентов системы. Для адиабатически изолиров. системы (dS =0) с фиксиров. числом частиц (dN = 0) выражение для dW определяется изменением внутр. энергии, 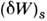= 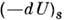для системы с фиксиров. темп-рой - изме-

нением её свободной энергии, (dW)s= -d(U-TS)_T= (-dF)_T и т. д.

Примеры. Р. пространственно однородной системы при изменении dV её объёма равна (р - давление; при наличии касательных напряжений выражение для dW составляется в соответствии с правилами теории упругости). Для поверхностной плёнки 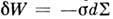(s - коэф. поверхностного натяжения, S - площадь поверхности раздела фаз). Для гальва-нич. элемента 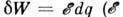- эдс элемента, dq- про-

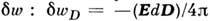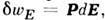
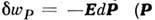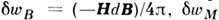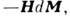
текший через него заряд). Для диэлектриков используют неск. вариантов выбора параметров состояния и соответствующих им выражений для удельной Р. - полная Р. ( Е- напряжённость электрич. поля, D - индукция); - поляризация диэлектрика). Для магнетика уд. Р.: = 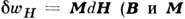- соответственно магн. индукция и намагниченность). Приведённые варианты для dw отличаются друг от друга на величины, являющиеся полными дифференциалами (для диэлектрика это ,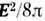 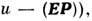к-рые можно включить в дифференциал внутр. энергии dU, поэтому каждому из выборов x_i соответствует согласованное определение величин 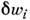и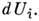

Лит. см. при ст. Термодинамика.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.