Akademik

КАРНО ЦИКЛ

КАРНО ЦИКЛ: обратимый круговой процесс, в к-ром совершается превращение теплоты в работу (или работы в теплоту). К. ц. состоит из последовательно чередующихся двух изотермич. и двух адиабатич. процессов, осуществляемых с рабочим телом (напр., паром). Впервые рассмотрен франц. физиком Н. Л. С. Карно (1824) как идеальный рабочий цикл теплового двигателя, совершающего работу за счёт теплоты, подводимой к рабочему телу в изотермич. процессе. Рабочее тело последовательно находится в тепловом контакте с двумя тепловыми резервуарами (имеющими постоянные темп-ры) — нагревателем (с темп-рой TI) и холодильником (с T2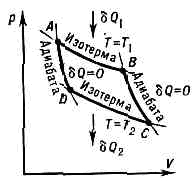
Цикл Карно на диаграмме р — V (давление — объём). dQ1 — кол-во теплоты, получаемой рабочим телом от нагревателя, dQ2—кол-во теплоты, отдаваемой им холодильнику. Площадь, ограниченная изотермами и адиабатами, численно равна работе цикла Карно.

Превращение теплоты в работу сопровождается переносом рабочим телом определ. кол-ва теплоты от нагревателя к холодильнику. К. ц. осуществляется след. образом (рис.): рабочее тело (напр., пар в цилиндре под поршнем) при темп-ре Т1 приводится в соприкосновение с нагревателем и изотермически получает от него кол-во теплоты dQ1 (при этом пар расширяется и совершает работу). На рисунке этот процесс изображён отрезком изотермы АВ. Затем рабочее тело, расширяясь адиабатически (по адиабате ВС), охлаждается до темп-ры T2 и приводится в тепловой контакт с холодильником. При этой темп-ре, сжимаясь изотермически (отрезок CD), рабочее тело отдаёт кол-во теплоты dQ2 холодильнику. Завершается К. ц. адиабатным процессом (отрезок DA), возвращающим рабочее тело в исходное термодинамич. состояние. При пост. разности темп-р (T1-T2) между нагревателем и холодильником рабочее тело совершает за один К. ц. работу

dA=ddQ1-dQ2=((T1-T2)/T1)dQ1.

Эта работа численно равна площади АВCD, ограниченной отрезками изотерм и адиабат, образующих К. ц.

К. ц. обратим и его можно осуществить в обратной последовательности (в направлении ADCBA). При этом кол-во теплоты dQ2 отбирается у холодильника и передаётся нагревателю за счёт затраченной работы dА. Тепловой двигатель работает в этом режиме как идеальная холодильная машина. К. ц. имеет наивысший кпд h=d/dQ1=(T1-T2)/Т1 среди всех возможных циклов, осуществляемых в одном и том же температурном интервале (Т1 -Т2) (см. КАРНО ТЕОРЕМА). В этом смысле кпд К. ц. служит мерой эффективности др. рабочих циклов.

Исторически К. ц. сыграл важную роль в развитии термодинамики и теплотехники. С его помощью была доказана эквивалентность формулировок К. Клаузиуса и У. Томсона (Кельвина) второго начала термодинамики; К. ц. был применён для определения абс. термодинамич. шкалы темп-р (см. ТЕМПЕРАТУРНЫЕ ШКАЛЫ); часто использовался для вывода разл. термодинамич. соотношений (напр., (см. КЛАПЕЙРОНА — КЛАУЗИУСА УРАВНЕНИЕ)).

КАРНО ЦИКЛ

- круговой обратимый процесс, состоящий из двух изотермич. и двух адиабатич. процессов. Впервые рассмотрен Н. Л. С. Карно в 1824 как идеальный цикл для теплового двигателя, в к-ром рабочее вещество приводят в тепловой контакт с двумя тепловыми резервуарами: нагревателем (с темп-рой T₁) и холодильником (с темп-рой T₂<T₁). На рис. изображён К. ц. для идеального газа, координатами служит давление Р и объём V. Сначала рабочее вещество приводят в тепловой контакт с нагревателями, а затем оно изотермически расширяется, получая от нагревателя теплоту dQ₁ и совершая работу (кривая АВ). После этого рабочее вещество расширяется адиабатически (кривая ВС )и охлаждается до темп-ры Т₂.Затем устанавливают тепловой контакт с холодильником иизотермически сжимают рабочее вещество, отбирая теплоту dQ₂ (линия CD). Завершают К. ц. адиабатич. сжатием рабочего вещества (отрезок DA), возвращая его в исходное состояние. В результате внутр. энергия рабочего вещества не изменяется, поэтому произведённая работа соответствует разности dQ₁-dQ₂.

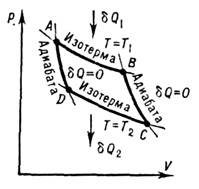
Цикл Карно для идеального газа на диаграмме Р-V. Площадь ABCD численно равна совершаемой работе.

Если проводить процесс в обратном направлении, то, совершая работу, можно передать часть теплоты от холодильника к нагревателю (обратный К. ц.). Анализируя К. ц., можно доказать Карно теорему о макс. кпд тепловых машин, h=(T₁-T₂)/T₁, это доказательство используют для формулировки второго начала термодинамики. Лит. см. при ст. Термодинамика. Д. Н. Зубарев.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.