Akademik

TURBULENCE

Le mot turbulence fait songer à agitation, désordre, chaos. L’évolution spatiale ou temporelle de nombreux phénomènes est caractérisée par l’absence apparente d’ordre, la coexistence d’échelles très différentes, l’impossibilité d’une reproduction et d’une prévision détaillées. Un tel comportement est qualifié de turbulent.

Les écoulements fluides en offrent les illustrations les plus courantes, rafales de vent ou tourbillons d’un torrent, et ce sont des hydrauliciens, en particulier J. Boussinesq et O. Reynolds, qui ont identifié vers la fin du XIX^e siècle deux régimes d’écoulement, l’un régulier ou laminaire , l’autre irrégulier ou turbulent , jouissant de propriétés très différentes, notamment pour la diffusion des grandeurs attachées au fluide. La méthode statistique fut naturellement utilisée pour ce problème aux applications nombreuses et importantes, par des chercheurs comme L. Prandtl, G. I. Taylor, T. von Karman, A. N. Kolmogorov, A. A. Townsend, S. Corrsin et R. H. Kraichnan. Nous possédons aujourd’hui une assez bonne description phénoménologique de la turbulence des fluides, une compréhension générale de sa dynamique, et des méthodes approchées de prévision de ses effets. L’approche statistique n’a cependant pas connu dans ce domaine un succès aussi complet que dans d’autres. Un écoulement turbulent combine en effet des structures tourbillonnaires dont les échelles couvrent une gamme large et continue, et qui sont toutes en forte interaction par suite de la non-linéarité des équations de Navier-Stokes. L’effet des petites structures limite donc la prédicibilité des grosses, dont l’influence compromet l’universalité du comportement statistique des petites.

L. Landau avait associé le chaos turbulent à la présence d’un très grand nombre de degrés de liberté, mis en jeu après un nombre équivalent de bifurcations des solutions des équations de Navier-Stokes. D. Ruelle et F. Takens ont introduit en 1971 des conceptions radicalement nouvelles sur la nature et le mécanisme d’apparition de la turbulence, qui étendent considérablement le domaine d’application de cette notion. La turbulence est associée ici à un comportement chaotique intrinsèque des systèmes dynamiques dissipatifs, caractérisé par un attracteur étrange dans l’espace des phases. Objet de vérifications, riche de possibilités bien qu’encore éloignée des calculs pratiques, cette conception offre un cadre théorique unifié à l’étude du comportement chaotique de systèmes aussi différents que ceux de la chimie, de l’optique, de l’aérodynamique, de la dynamique des populations, par exemple.

1. Approches théoriques du concept

Depuis les années soixante-dix, on a étudié bien des systèmes appartenant à des domaines scientifiques variés et présentant des comportements chaotiques, mais la notion de turbulence n’a jamais été définie. On peut toutefois tenter de dégager un certain nombre de caractéristiques propres à cet ensemble de systèmes: un ou plusieurs paramètres, dits de contrôle, gouvernent leur évolution; ces systèmes présentent généralement divers états ordonnés de complexité croissante avant que la turbulence n’apparaisse; ils passent d’un état à un autre d’une façon soudaine, appelée bifurcation, et parfois ils présentent un phénomène d’hystérésis; généralement, un petit nombre de ces bifurcations (trois ou quatre) amène le système du repos à l’état chaotique; enfin, et c’est très important, lorsque celui-ci est atteint, des systèmes se trouvant dans des états initiaux très voisins évolueront d’une façon totalement différente: on dit qu’ils présentent une sensibilité aux conditions initiales (cf. figure), ces évolutions différentes étant toutefois associées à des évolutions statistiques identiques, si les deux conditions initiales satisfont à certaines restrictions.

Il existe deux tentatives d’explication théorique: la théorie de L. Landau, construite dans les années 1940 pour la turbulence fluide, mais qui ne rend pas compte de l’ensemble des caractéristiques évoquées plus haut, et la théorie de Ruelle-Takens, qui semble aujourd’hui très féconde.

La théorie de L. Landau

Rappelons que les équations de Navier-Stokes font apparaître une quantité R, appelée le nombre de Reynolds, qui est le paramètre de contrôle des écoulements hydrodynamiques. Pour de faibles valeurs de R, les solutions stationnaires des équations sont stables. Pour des valeurs plus élevées, on doit rechercher des solutions périodiques de la forme:

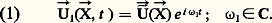
Du fait de la présence de perturbations inconnues dans l’écoulement, ぴ¹ ne peut pas être totalement déterminée: le système présente un degré de liberté. Lorsque R augmente encore, ぴ¹ se déstabilise à son tour, et une fréquence 諸², incommensurable avec 諸¹, apparaît, associée à un deuxième degré de liberté. Ce processus se poursuit et l’on aboutit, à la limite, à une solution quasi périodique (spectre de raies) à une infinité de degrés de liberté.

Ce type de théorie ne traduit pas la notion fondamentale de sensibilité aux conditions initiales; le chaos n’y est pas intrinsèque mais est lié à la présence de perturbations aléatoires extérieures; le spectre est constitué de raies qui, à l’issue de trois ou quatre bifurcations, ne pourront jamais être suffisamment proches pour être confondues avec un spectre continu. Ce cadre explicatif n’est donc pas satisfaisant, même si une suite de bifurcations quasi périodiques existe dans certaines circonstances exceptionnelles.

La théorie de Ruelle-Takens

Les systèmes étudiés sont les systèmes dissipatifs modélisés par des équations différentielles, dont l’évolution est décrite par la trajectoire d’un point dans un espace H, appelé espace des états ou espace des phases, de dimension N égale au nombre de réels nécessaires à la spécification de la condition initiale: les systèmes hydrodynamiques apparaissent donc comme «infini-dimensionnels». D. Ruelle et F. Takens conjecturent que, quel que soit N, la suite des bifurcations vers la turbulence lors de la variation de la valeur du paramètre de contrôle est construite de la façon suivante: des points fixes, des cycles limites, des tores puis des attracteurs très particuliers, appelés pour cette raison des attracteurs étranges, dont la structure géométrique et probabiliste est la traduction de l’évolution chaotique du système. Notre connaissance du chaos passe donc par celle de la structure de ces objets.

Le fait que pour des systèmes dissipatifs la mesure de l’élément de volume décroisse de façon monotone implique qu’ils évoluent vers un sous-ensemble de H, de mesure de Lebesgue nulle: l’attracteur. Celui-ci peut être: un point fixe (état stationnaire), un cycle limite (état périodique), un tore (état quasi périodique), ou un attracteur étrange (état chaotique). On peut utiliser, pour caractériser la nature géométrique ou probabiliste d’ensembles, diverses définitions de la notion de dimension.

Trois d’entre elles sont particulièrement utilisées:

– la dimension topologique D^T, toujours entière, qui est celle à laquelle nous sommes habitués;

– la dimension fractale D^F, qui décrit la façon dont un objet emplit l’espace dans lequel il est plongé;

– la dimension d’information D^I, qui décrit la façon dont l’attracteur est «visité» et qui s’identifie à D^F si tous les points de l’attracteur ont même probabilité: D^F et D^I ne sont pas forcément entières.

Les trois premières sortes d’attracteurs citées plus haut sont de nature simple: les trois dimensions D^T, D^F, D^I sont égales et entières. Cela n’est pas le cas pour les attracteurs étranges, ce qui implique que le chaos est associé aux valeurs non entières de D^F et D^I, strictement inférieures à N et supérieures ou égales à D^T.

Appelons n ( 﨎) le nombre de boules Ndimensionnelles de rayon 﨎 nécessaires à la construction d’un recouvrement de l’attracteur à la précision 﨎. On appelle résolution :

et dimension fractale :

Appelons p ^it la probabilité de présence dans la boule i . On appelle information :

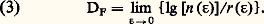
et dimension d’information :

Du fait que lg (n ( 﨎)) 閭 I( 﨎), la dimension fractale est plus grande que la dimension d’information. Il convient de noter que la différence entre ces deux dimensions est liée à la non-uniformité de la probabilité sur l’attracteur, ou non-ergodicité .

L’entropie métrique précise la notion de chaos. Considérons à nouveau le recouvrement de l’attracteur. Soit une suite S^j (m ) de mesures successives effectuées à des intervalles de temps t et soit P[S^j (m )] la probabilité de cette suite, normalisée de telle sorte que:

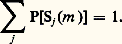
L’information contenue dans cette suite est donnée par:

On appelle entropie métrique la quantité maximale d’information contenue par unité de temps dans toutes les suites finies 塚:

Pour les systèmes prédicibles, de nouvelles mesures n’apportent pas d’information nouvelle et h = 0, alors que pour les systèmes chaotiques h 礪 0. Dans la majeure partie des situations, on peut considérer que h est une caractéristique de l’attracteur.

Le spectre des exposants de A. M. Lyapounov, lié à l’évolution de l’élément de volume dans H, résume les propriétés de stabilité locale de l’attracteur. Il existe en outre de bonnes raisons de penser que l’entropie métrique et la dimension d’information sont liées à ce spectre.

Soit une boule de rayon 﨎(0) à t = 0 et soit 﨎ⁱ (t ) la longueur des axes principaux de l’ellipsoïde dans lequel elle est plongée à l’instant t . On appelle exposants de Lyapounov les quantités suivantes:

Les valeurs négatives de ces exposants représentent la convergence des trajectoires vers l’attracteur, les valeurs positives leur divergence sur celui-ci, divergence liée à la sensibilité aux conditions initiales. Leur somme doit être strictement négative, du fait qu’elle est associée à la décroissance de la mesure de l’élément de volume de H.

Pour les systèmes suffisamment dissipatifs, ces exposants sont une caractéristique de l’attracteur. On a remarqué que la quantité suivante, appelée dimension de Lyapounov , était probablement égale à la dimension d’information:

où j est le plus grand entier pour lequel:

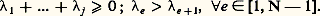
Par ailleurs, on a montré dans certains cas, et vérifié dans d’autres, que l’entropie métrique est égale à:

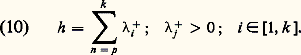
Grâce à la notion de corrélation intégrale:

où H est la fonction échelon, il est possible de mesurer expérimentalement la dimension d’information d’un attracteur, même si l’on ignore la dimension de l’espace des phases. Cette méthode est actuellement exploitée dans des cas réels.

Quelques systèmes dynamiques bas-dimensionnels ont été particulièrement étudiés. Ce sont les attracteurs de M. Hénon, de E. Lorenz et l’application logistique. Cette dernière présente une suite de bifurcations analysée par M. J. Feigenbaum et décelée par A. Libchaber et J. Maurer dans des expériences très délicates sur l’hélium liquide.

Les systèmes haut-dimensionnels sont l’axe des recherches actuelles. Des expériences numériques sur des systèmes comportant un grand nombre d’exposants de Lyapounov n’ont montré aucune contradiction avec la théorie de Ruelle-Takens. Aussi, cette dernière apparaît-elle actuellement comme un modèle très crédible de l’établissement du chaos.

2. Quelques suites de bifurcations vers la turbulence

On a tenté, depuis les années soixante-dix, d’unifier les méthodes d’étude des relations ordre-chaos par la création d’une nouvelle discipline, la synergétique, cherchant à créer une attitude transdisciplinaire dans des domaines comme les mathématiques, la physique, la chimie, la biologie, l’écologie ou la linguistique. Ce processus n’étant que partiellement engagé, nous ne décrirons ici que quelques aspects des instabilités et de la turbulence chimiques ainsi que quelques situations typiques de mécanique des fluides, eu égard à l’importance qualitative ou pratique particulière des études menées dans ces domaines.

Instabilités et turbulence chimiques

W. C. Bray découvrit en 1917 la première réaction périodique. B. P. Belousov montra en 1958 que ce caractère existait dans une nouvelle réaction dont A. Zhabotinsky, en 1966, dégagea la structure spatiale. Cette réaction dont le paramètre de contrôle est le débit en produits frais concerne l’oxydation de l’acide citrique par les ions Br^3- en milieu acide, catalysée par le couple Ce³⁺⁺/Ce⁴⁺⁺: il en existe des formes avec ou sans agitation.

En absence d’agitation, des structures organisées s’établissent spontanément dans le mélange initialement homogène. Avec agitation, un phénomène d’hystérésis, lié à la non-unicité du résultat pour des conditions expérimentalement identiques, rappelle la nécessité d’affiner la notion de répétabilité expérimentale. Lors de l’augmentation du paramètre de contrôle, on peut observer le phénomène suivant: une oscillation associée à une seule fréquence fondamentale, puis une bifurcation périodique-quasi périodique présentant ou non un phénomène d’accrochage de phase, puis un régime chaotique (premier cas à être analysé suivant le concept d’attracteur étrange), enfin, curieusement, un état stationnaire lié en fait à l’insuffisance du temps de présence des produits dans le réacteur.

Cette réaction, du fait de sa souplesse d’utilisation et de la très grande valeur (70 dB) de son rapport signal sur bruit (appréciable lors de l’étude des trajectoires dans l’espace des phases), pourrait constituer un candidat privilégié parmi les phénomènes utilisés pour l’analyse de l’établissement de la turbulence.

Instabilités hydrodynamiques

On peut classer les instabilités hydrodynamiques en distinguant les situations idéalisées, de Rayleigh-Bénard et de G. I. Taylor, des situations concrètes, couches limites et couches cisaillées ou écoulements géophysiques. Les moyens d’études théoriques sont, d’une part, la théorie de la stabilité (linéaire ou non linéaire) et, d’autre part, de façon plus globalisante, la théorie des bifurcations.

Dans la situation de Rayleigh-Bénard, on porte à des températures ¹ et ², ¹ 閭 ² les faces inférieure et supérieure d’une boîte horizontale emplie de fluide. L’influence relative de la gravité et des propriétés moléculaires du fluide est traduite par le paramètre de contrôle Ra, nombre de Rayleigh. On appelle rapport d’aspect r le rapport entre les dimensions horizontale et verticale de la boîte. Pour r = 2, on observe la même suite de bifurcations que dans la réaction de Belousov-Zhabotinsky, à l’exception de l’état stationnaire de celle-ci. Pour des valeurs plus grandes de r , la transition à la turbulence est plus brutale du fait de l’augmentation du nombre de degrés de liberté: une telle turbulence est dite de phase. Si la boîte n’a pas de face supérieure, des effets de tension superficielle viennent se combiner aux forces de gravité. Les instabilités qui apparaissent dans cette configuration sont dites de Bénard-Marangoni.

Pour l’étude de l’instabilité de Taylor, le fluide est disposé entre deux tubes coaxiaux. On utilise principalement deux types de fonctionnement: le tube interne en rotation uniforme et le tube externe fixe, ou l’inverse. Dans la première configuration, l’ensemble des comportements décrits pour la réaction de Belouzov-Zhabotinsky et l’instabilité de Bénard sont encore observés, ainsi d’ailleurs que le phénomène d’hystérésis. Dans le second type de fonctionnement, une seule bifurcation conduit à un état turbulent intermittent présentant des bouffées laminaires alternant avec des bouffées turbulentes. Ce type de bifurcation est dit sous-critique et montre l’existence de deux attracteurs visités alternativement. Par opposition, les bifurcations existant dans les autres cas sont dites sur-critiques : elles se produisent pour des valeurs du paramètre de contrôle supérieures à celle de la théorie linéaire.

Ce phénomène d’intermittence se retrouve dans la configuration de J. L. Poiseuille, où le fluide s’écoule dans un tube cylindrique ou annulaire. En ce qui concerne le problème classique de la transition de la couche limite, la première bifurcation est en général bidimensionnelle et sur-critique, les étapes suivantes étant tridimensionnelles et caractérisées par l’apparition de spots de turbulence . Les écoulements cisaillés libres, jets, sillages ou couches de mélange, sont particulièrement propices au développement de structures bidimensionnelles, subissant parfois des bifurcations sous-harmoniques correspondant à la coalescence de tourbillons, avant la naissance des structures tridimensionnelles associées à l’apparition proprement dite de la turbulence (cf. photo).

Il existe encore bien d’autres circonstances de développement d’instabilités hydrodynamiques. Ainsi, dans les milieux fluides géophysiques, les effets combinés du cisaillement des vitesses, de la stratification stable ou instable des densités et de la rotation donnent naissance à une grande variété d’instabilités spécifiques.

On voit que l’ensemble des systèmes bas-dimensionnels précédemment évoqués, la réaction de Belousov-Zhabotinsky, les instabilités de Bénard et Taylor, confirment pleinement la théorie de Ruelle-Takens. L’analyse des situations réelles de dimensions élevées commence à être conduite suivant ses concepts.

3. Description statistique pour les fluides usuels

Approche statistique

Les caractéristiques statistiques de toute variable attachée au fluide 福﨡, considérée fonction aléatoire de l’espace ぷ et du temps t , sont définies à l’aide d’un opérateur de moyenne: ^-. On invoque l’ergodicité pour l’assimiler à une moyenne temporelle ou spatiale, et on suppose vérifiées les règles de Reynolds:

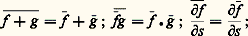
pour s = t , ぷ. Il est admis par ailleurs que tous les détails du phénomène restent régis par le système classique d’équations de bilan de la thermodynamique linéaire des processus irréversibles:

où apparaissent la vitesse locale de variation:

les divergences des flux de convection par le mouvement du fluide, 福﨡 V^j , et de diffusion par les processus moléculaires, J^j ( 福﨡), ainsi que le débit des sources ou puits, 靖( 福﨡). L’application de l’opérateur de moyenne à (12) conduit à une équation statistique de bilan , dont l’écriture nécessite de séparer les différentes variables en la somme de valeurs moyennes et de fluctuations turbulentes, 﨡 = 﨡 黎 + 﨡 . Pour que la vitesse moyenne représente la vitesse moyenne de convection de la masse, il faut utiliser des moyennes (de Favre) pondérées par la masse:

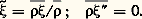
On peut souvent négliger les fluctuations de 福 et utiliser la décomposition (de Reynolds):

conduisant à l’équation moyenne de bilan:

Dans le bilan moyen de la variable considérée, apparaît donc un flux de diffusion turbulente , traduisant l’effet moyen du transport convectif de la fluctuation 﨡 par la fluctuation de vitesse v ^j . Ce flux turbulent est en général très supérieur au flux moléculaire, et affecte profondément les équations moyennes (13). Il constitue une inconnue supplémentaire, et rend donc le système indéterminé, d’où le recours à des hypothèses, dites de fermeture, pour lever cette indétermination. Ainsi, par exemple, l’écoulement turbulent avec transfert de chaleur est régi, avec des approximations classiques, par le système:

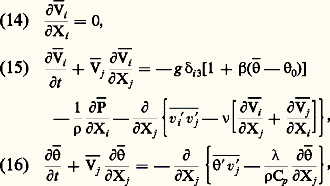
où apparaissent les tensions de Reynolds, v ⁱ v ^j , et les flux turbulents de chaleur, 福C^p v ^j .

Modélisation des effets

Les premières hypothèses de fermeture reposent sur des analogies avec la formulation des flux moléculaires. J. Boussinesq a introduit des coefficients de diffusivité turbulente, 阮t , 﨡, tels que:

correspondant au produit d’une vitesse et d’une distance caractéristiques. L. Prandtl a proposé une longueur de mélange , l , analogue à un libre parcours moyen, telle que:

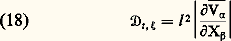
Le problème est ramené à la prévision de 阮^t ou l , ce qui est possible par des considérations dimensionnelles et phénoménologiques simples dans les cas courants, mais ne l’est plus dans les écoulements complexes ou évolutifs. Il faut alors revenir aux équations instantanées, qui permettent par exemple d’établir l’équation de bilan de l’énergie cinétique de la turbulence, k 漣 = 1/2(v ⁱ v ⁱ ):

où l’on identifie des taux de production P, depuis l’énergie cinétique du mouvement moyen, de production ou destruction A, par le travail des forces d’Archimède, de dissipation 﨎, en chaleur par viscosité, et un flux spatial, T^j . On ferme alors le système en faisant u = (k 漣)^1/2, en adoptant des relations phénoménologiques telles que 﨎 = C ^te . u ³/l , et en déduisant l de considérations géométriques ou d’équations d’évolution, telle celle pour 﨎.

Le concept de diffusivité turbulente est mis en échec dans les zones de flux turbulent à contre-gradient, longtemps perçues comme des hérésies thermodynamiques. On a alors recours aux équations de bilan des moments d’ordre deux, et même trois, fermées à partir de considérations théoriques et phénoménologiques. Une tentative (E. Hopf) de considérer l’ensemble de la hiérarchie des équations aux moments n’a pas abouti à des résultats concrets. Le calcul numérique direct de toute la gamme, ou seulement des plus grosses, des structures d’écoulements turbulents à petits ou grands nombres de Reynolds s’est beaucoup développé du fait des capacités données par l’informatique.

Structure interne

La description de la structure interne utilise des fonctions spectrales , transformées de Fourier des moments en plusieurs points, les corrélations. Dans le cas idéal d’une turbulence homogène et isotrope , il suffit d’une fonction E(k ) caractérisant la répartition de l’énergie de la turbulence entre les nombres d’ondes k . L’équation fondamentale de la dynamique spectrale:

dont l’intégration en k conduit à une version simplifiée de (19):

met en évidence un mécanisme fondamental d’interaction non linéaire entre triades, や + ら + り = 0, de vecteurs d’ondes, responsable d’un échange d’énergie (marqué d’ailleurs par une intermittence interne spatiale et temporelle) entre ces vecteurs et qui soulève un problème de fermeture spectrale, aujourd’hui assez bien résolu.

En turbulence classique à trois dimensions (A. N. Kolmogorov), l’interaction dans la zone dite inertielle se fait par extension de filets tourbillonnaires d’échelles décroissantes, avec accroissement de la grandeur appelée «enstrophie», et l’énergie injectée à relativement grande échelle cascade au taux 﨎 vers des échelles de plus en plus petites, pour finalement être dissipée vers k ^d = 﨎^1/4 益 size=1^漣3/4. En turbulence à deux dimensions (G. Batchelor, R. H. Kraichnan), l’énergie et l’enstrophie injectées simultanément à une échelle intermédiaire cascadent à des taux 﨎 et 廓 dans des directions opposées: l’enstrophie vers les petites échelles pour être dissipée par viscosité vers k ^e = 廓^1/6 益 size=1^漣1/2, l’énergie vers de plus en plus grandes échelles, où elle finit par être absorbée. Les dynamiques internes sont très différentes: à trois dimensions, fragmentation des structures, interactions locales (face=F0019 瑩 や 瑩 力 瑩 ら 瑩) importantes, viscosité turbulente spectrale positive; à deux dimensions, coalescence de tourbillons, interactions non locales importantes, viscosité négative.

Les échelles de production de la turbulence réelle, liées d’après (19) à des interactions flux turbulents/gradients moyens, sont foncièrement anisotropes, mais la cascade tridimensionnelle s’accompagne d’une tendance croissante vers l’isotropie locale des petites structures. Les frontières des zones turbulentes jouent un rôle important: production intense par de petites structures assez organisées près des parois; présence d’une interface nette mais très contournée (d’où apparition d’un nouveau type d’intermittence) à la limite externe, avec entraînement progressif du fluide non turbulent (cf. photo). Un problème capital mal élucidé est la présence de grosses structures relativement cohérentes et spécifiques à chaque écoulement, qui est à la base des difficultés des fermetures physiques ou spectrales. Leur comportement présente parfois des similitudes troublantes avec certains mécanismes de bifurcations.

4. Domaines d’application

Diffusion dans les écoulements turbulents

La propriété de diffusion dans les écoulements turbulents, essentielle, relève d’une théorie de la diffusion par des mouvements continus (G. I. Taylor), qui prévoit des déplacements relatifs des particules fluides gaussiens, de variance:

où 福ⁱⁱ ( 精) = Vⁱ (t , ぷ)Vⁱ (t + 精, ぷ)/v^{i 2} est un coefficient d’autocorrélation lagrangien. Dans un écoulement sans vitesse moyenne avec un temps intégral 淪ⁱⁱ lagrangien fini, la diffusivité tend asymptotiquement vers:

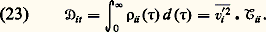
Avec une vitesse moyenne cisaillée, la dispersion longitudinale est considérablement accrue par les différences dans le transport moyen, et il vient asymptotiquement:

Les calculs effectifs de dispersion de contaminants sont possibles au prix de différentes

hypothèses: ainsi, la dispersion d’une «bouffée» correspond souvent à une diffusivité croissant comme la puissance 4/3 de son diamètre (L. F. Richardson); dans les situations pratiques, la diffusion par cisaillement est essentielle, la turbulence inhomogène, et les méthodes relativement empiriques.

La diffusion moléculaire modifie la répartition des concentrations: en son absence, la turbulence répartirait une «tache» de contaminant en une infinité de feuillets de même concentration; en sa présence, elle accroît à la fois la surface de contact et les gradients locaux, d’où une homogénisation rapide à petite échelle. Cette intensification du rôle des phénomènes moléculaires présente la propriété remarquable, due à l’existence de cascades non linéaires, de leur être imposée par les grandes échelles, indépendamment de leur efficacité propre, qui n’intervient que pour fixer celles auxquelles ils agissent effectivement.

Dans la pratique, l’effet de la diffusion par la turbulence est généralement traité par les approches eulériennes évoquées plus haut. On voit alors apparaître la possibilité de modifications de la structure de la turbulence par des forces liées à la grandeur diffusée, d’où la distinction entre contaminants passifs et actifs.

Aérodynamique et hydrodynamique

L’écoulement turbulent près de corps en mouvement relatif est en général du type couche-limite, ce qui se traduit par une diminution progressive de la diffusivité turbulente au voisinage de la paroi, un transfert d’énergie efficace, un profil de vitesses plat dans la zone externe, un gradient de vitesse et un frottement accrus dans la zone interne. Pour réduire les traînées de frottement, on cherche donc à retarder la transition (poli, géométrie) ou à diminuer l’effet de la turbulence (polymères ou fibres). Pour retarder les décollements, et donc réduire les traînées de forme et accroître les portances, il faut au contraire développer la turbulence (rugosités).

Le caractère fluctuant des efforts exercés par le fluide soulève des problèmes de vibration des structures mécaniques. Les écoulements turbulents possèdent d’ailleurs la capacité intrinsèque d’engendrer du bruit. Ce bruit est dû à des sources virtuelles quadripolaires convectées au sein de la zone de turbulence (M. J. Lighthill, J. E. Ffowcs-Williams), plus ou moins compactes suivant les échelles de cette dernière. On lutte contre ces effets en diminuant les échelles et les gradients des vitesses (réacteurs à double flux).

Dans les écoulements compressibles, aux fluctuations de vitesse et de pression s’ajoutent des fluctuations de température (d’origines réversible et irréversible), et le champ turbulent a été parfois séparé en modes rotationnel, entropique et acoustique (Kovasznay) en interactions. Les fluctuations de la masse spécifique doivent être prises en compte dans l’expression des divers bilans, mais la structure générale est assez peu modifiée aux nombres de Mach modérés, sauf dans les interactions choc/turbulence.

Génies thermique et chimique

Les utilisations délibérées les plus anciennes et les plus courantes de la turbulence concernent l’intensification des transferts de chaleur et de matière au sein des fluides ou vers les parois qui les limitent. Dans le second cas, l’effet de la diffusion moléculaire à proximité immédiate de la paroi est déterminant, car la diffusion turbulente y tend vers zéro dans les sous-couches visqueuses sur parois lisses, ou y intervient par des forces de pression à petite échelle sans action sur le transfert de contaminants scalaires sur parois rugueuses. La diffusivité turbulente au sein du fluide étant élevée et pratiquement indépendante de la grandeur transférée, lorsque les nombres de Prandtl Pr= 益福 C^p / ou de Schmidt Sc = 益/ 阮 sont voisins de 1, une étroite analogie, dite de Reynolds, existe entre les transferts tangentiels de quantité de mouvement et ceux de chaleur ou de masse, sur parois lisses. Sur parois rugueuses, ou lorsque Pr et Sc diffèrent notablement de l’unité, les résistances aux transferts de la quantité de mouvement et des grandeurs scalaires peuvent être très différentes. Aux interfaces liquide-gaz, des complications nouvelles surgissent, et la modélisation des transferts utilise souvent un concept de renouvellement turbulent des masses fluides interfaciales.

L’efficacité des mélanges et réactions chimiques résulte d’une agitation turbulente spontanée ou artificielle. Dans les réactions de combustion, les transferts de masse et de chaleur sont intimement associés, et le débit des sources ou puits de chaque constituant dépend des concentrations des autres et, très fortement, de la chaleur dégagée par la réaction. De tels couplages sont générateurs par eux-mêmes d’un comportement turbulent, qu’une turbulence d’origine hydrodynamique vient souvent accentuer. Son analyse devra tenir compte des fortes variations de 福 et faire appel à des distributions de probabilité multidimensionnelles pour la modélisation de couplages fortement non linéaires.

Environnement

La circulation des milieux fluides géophysiques, en particulier océans et atmosphères, est aujourd’hui considérée comme turbulente à toutes les échelles. Aux plus grandes, les mouvements sont surtout horizontaux, en raison de la géométrie (H/L 廉 1) et de la stratification en densité que caractérise la fréquence de Brunt-Väisälä:

et profondément influencés par la force de Coriolis due à la rotation (avec V, L vitesse et échelle horizontales, 行 vitesse de rotation, 﨏 latitude, le nombre de Rossby Ro = V/2 行 sin 﨏 L = V/f L est 廉1). La turbulence quasi géostrophique qui leur correspond présente de frappantes similitudes avec le modèle de turbulence à deux dimensions, comme la viscosité négative et la prédicibilité limitée, similitudes dont la portée est cependant bornée par des mécanismes comme l’instabilité barocline ou le développement d’ondes de C. G. Rossby.

Aux petites échelles, on observe en géophysique une turbulence tridimensionnelle à grand nombre de Reynolds, due aux effets combinés des cisaillements de la vitesse moyenne et de la stratification verticale de la densité. D’après (19), leur importance relative dans le bilan d’énergie de la turbulence est caractérisée par le nombre de Richardson:

Dans les zones stables, en particulier celles à fort gradient (inversion et thermocline) qui se créent à la limite des couches bien mélangées, les forces d’Archimède travaillent contre la turbulence, avec la dissipation, et en arrivent à la faire disparaître lorsque Rf atteint + 1/4. Ces zones stables font obstacle à la diffusion, mais sont perturbées par des ondes internes susceptibles d’engendrer, par instabilité de Kelvin-Helmholtz, des déferlements turbulents sporadiques. Dans les cas instables, la turbulence est au contraire favorisée, et à la limite créée, par les effets gravitationnels, d’où des transferts intenses qui ne peuvent se maintenir que par utilisation de l’énergie potentielle libérée par le rayonnement et les changements de phase de l’eau. Des zones convectives (couche limite planétaire et convection profonde nuageuse) sont ainsi créées dans l’atmosphère, plus rarement dans l’océan (sources d’eaux profondes).

L’atmosphère et les océans constituent une gigantesque machine thermique, régulatrice du climat, dans le fonctionnement de laquelle la turbulence joue un rôle essentiel, ce qui explique la difficulté de sa prévision. En outre, la turbulence détermine les grands cycles biogéochimiques et intervient dans le traitement éventuel et la dilution des effluents qui viennent les perturber.

Problèmes divers

La turbulence joue un rôle dans la dynamique des fluides polyphasiques, notamment pour créer et maintenir des phases dispersées. Le comportement de petites particules en suspension dépend évidemment de leur inertie, de leur poids relatif et de l’effort de traînée fluctuant imposé par le fluide, d’où des écarts de vitesse et des interactions complexes. À citer encore l’action sur les sédiments et le rôle déterminant des gradients locaux dans les mécanismes de coalescence ou de captation.

Les fluctuations de température et de composition d’un milieu turbulent agissent sur son indice de réfraction pour les ondes électromagnétiques ainsi que sur la célérité de propagation des ondes acoustiques relativement à un champ de vitesse lui-même fluctuant. Il en résulte des effets de diffusion, appréciables lorsque la condition de Bragg est remplie, et dont une théorie linéarisée (V. I. Tatarskii) donne les sections efficaces en fonction de paramètres comme les taux de destruction moléculaire de différents moments. L’effet sur le rayonnement propagé est traduit par exemple par la scintillation des sources éloignées. Ces phénomènes sont à la base de puissantes méthodes de télédétection.

5. Applications en météorologie

Les écoulements atmosphériques sont turbulents: l’importance de ce phénomène pour les applications météorologiques et environnementales ont fait de l’atmosphère un milieu privilégié pour son étude. C’est la faible viscosité de l’air, eu égard aux dimensions du milieu, qui donne naissance à des nombres de Reynolds très élevés (de 10⁶ à 10⁹). L’écoulement recèle donc de nombreuses échelles de mouvement en interaction; par conséquent, le traitement simultané, théorique ou numérique, de l’ensemble du spectre se révèle extrêmement complexe. Les modèles théoriques issus de la recherche en turbulence guident la compréhension des grands cycles énergétiques de l’atmosphère, la conception d’expériences et l’interprétation des résultats. Ils décrivent les propriétés de la turbulence atmosphérique, variables suivant l’échelle horizontale des mouvements concernés. Par commodité, on répartit ces mouvements en trois classes: les mouvements de grande échelle, qui relèvent d’une théorie bidimensionnelle, les mouvements de petite échelle, qui nécessitent une approche tridimensionnelle, et les mouvements d’échelle intermédiaire, ou méso-échelle, pour lesquels la théorie demeure embryonnaire.

L’approche pratique, pour représenter un écoulement atmosphérique, consiste à utiliser un modèle numérique pour résoudre sur une grille spatiale fixe les équations de la mécanique de l’atmosphère ^{[cf. PRÉVISION MÉTÉOROLOGIQUE]}. Ainsi, pour une prévision à quatre jours sur la France, on utilisait, au milieu des années 1990, un réseau de points espacés de 100 km sur l’horizontale, et de 1 km sur la verticale (sur 15 niveaux), couvrant tout l’hémisphère Nord. Une partie importante de la variabilité atmosphérique échappe à la représentation explicite sur les mailles de ce réseau, et doit être prise en compte de manière statistique: on dit qu’on paramètre les effets des échelles inférieures à la maille. Les lois de paramétrisation ainsi définies sont une des principales inconnues de la météorologie, et jouent un rôle analogue aux lois de comportement de la mécanique des milieux continus. Leur formulation est un domaine de recherche qui se fonde sur les résultats de la représentation statistique de la turbulence.

Mouvements de grande échelle

Aux échelles horizontales supérieures à 100 km, l’épaisseur réduite de l’atmosphère (10 km) et sa stabilité (résistance aux mouvements verticaux) font que le mouvement horizontal est comparable à celui d’une lame fluide bidimensionnelle. La théorie de la turbulence dans un espace à deux dimensions permet alors (en schématisant) de comprendre de nombreux aspects de ces mouvements. L’écoulement est caractérisé par sa vitesse horizontale de composantes u , v, en chaque point x , y d’un plan fermé S, et il y a conservation de l’intégrale de l’énergie cinétique:

et de l’enstrophie, ou carré du tourbillon absolu:

(le paramètre de Coriolis f exprimant l’influence de la rotation terrestre).

On peut montrer que l’existence de ces deux contraintes conditionne la forme du spectre de grande échelle de l’énergie cinétique E(k ). En particulier, on n’observe pas la formation d’une zone «inertielle», où E(k ) varie en k size=1^漣5/3, comme en turbulence tridimensionnelle, traduisant une cascade d’énergie vers les petites échelles, car cela serait incompatible avec la conservation de l’enstrophie. Le spectre énergétique d’équilibre correspond à une décroissance plus rapide de l’énergie avec le nombre d’onde, E(k ) 劣 見k ^-3, ce qui signifie que l’écoulement a une tendance naturelle, du fait de sa bidimensionnalité, à conserver des structures cohérentes, et à résister à la perte d’information qui se produit en turbulence tridimensionnelle. Cela a pour conséquence d’accroître considérablement la prévisibilité de l’atmosphère. Une confirmation expérimentale de cette théorie a été apportée par l’expérience franco-américaine Éole (1972), grâce à l’étude des trajectoires de centaines de ballons plafonnants dans l’hémisphère Sud. Néanmoins, l’incertitude subsiste quant à l’extension précise du domaine d’échelle qu’elle décrit.

L’analogie avec la turbulence bidimensionnelle permet l’étude de l’influence des erreurs initiales sur la prévision. On a pu montrer que l’addition d’une perturbation aléatoire, si petite soit-elle (effet «papillon»), contamine progressivement des échelles de plus en plus grandes, et affecte l’ensemble de l’écoulement global après environ quinze jours. C’est ce qui permet de fixer la limite de prévisibilité déterministe de l’atmosphère.

Les notions de conservation de l’énergie et de l’enstrophie sont des guides efficaces pour la recherche des techniques numériques les plus performantes dans les modèles météorologiques, et ont notamment mené au développement spectaculaire des méthodes dites de Galerkin, fondées sur la représentation des champs météorologiques par des bases de fonctions. Enfin, l’étude détaillée des transferts spectraux d’énergie et d’enstrophie conduit à des théories sur la meilleure représentation des mouvements d’échelle inférieure à la maille des modèles, et en particulier sur la formulation optimale de l’opérateur de diffusion horizontale.

Mésométéorologie

De 1 à 100 km s’étend le domaine de la «mésoéchelle», dont l’étude a connu une expansion considérable après l’apparition de moyens de calculs et de mesures assez puissants pour affiner la prévision synoptique et lui donner un usage pratique plus immédiat; la mésométéorologie étudie un ensemble varié de phénomènes, souvent liés à une excitation extérieure, comme le relief ou les contrastes thermiques ou hydriques de surface, ou à des développements nuageux: convection orageuse ou formes particulières d’instabilité dans les fronts à la limite de deux masses d’air. La recherche théorique et appliquée dans ces domaines est très active, mais n’a pas encore fourni de modèles aussi fructueux que ceux cités plus haut. Les principales difficultés à surmonter sont d’ordre géométrique: interactions de phénomènes bi- et tridimensionnels, description du caractère intermittent de la turbulence, dans l’espace comme dans le temps, qui nécessite le recours à de nouveaux formalismes mathématiques, comme la géométrie fractale.

Micrométéorologie

La turbulence tridimensionnelle, d’échelle inférieure où égale à 1 km environ, est présente en de nombreux endroits de l’atmosphère, comme sur les flancs des courants-jets, mais surtout au voisinage de la surface terrestre: la couche limite atmosphérique ainsi définie, qui constitue le domaine de la micrométéorologie, est une zone d’épaisseur variable, de quelques mètres à 3 km, où l’écoulement est en permanence turbulent sous l’influence des perturbations thermiques et dynamiques de la surface.

La présence d’une zone turbulente au voisinage du sol se manifeste par des effets systématiques qui affectent l’ensemble du comportement de l’atmosphère. Le ralentissement du vent par les obstacles de la surface provoque un transport vertical de quantité de mouvement qui contribue à répartir la décélération en altitude. Dans ce processus, la turbulence se maintient en tirant son énergie de l’écoulement de grande échelle, et représente donc une dissipation d’énergie importante. De plus, l’équilibre entre les forces de pression et celles de Coriolis est rompu, entraînant une déviation latérale du vent par rapport aux isobares, dans la direction des basses pressions. Cela donne naissance au phénomène de «pompage d’Ekman» ^{[cf. OCÉANS ET MERS]} qui, en créant des circulations secondaires dans les dépressions et les anticyclones, modifie les grands systèmes atmosphériques. Enfin, la chaleur et l’humidité disponibles à la surface terrestre sont réparties dans l’atmosphère par les mouvements turbulents à travers la couche limite, créant ainsi, à l’échelle planétaire, les contrastes thermiques dans la masse de l’atmosphère qui alimentent la machine météorologique. Les caractéristiques de la turbulence dans la couche limite atmosphérique interviennent donc à tous les niveaux du cycle énergétique, et doivent être prises en compte d’une manière très détaillée.

En simplifiant, on peut ramener le problème à la mesure et au calcul des flux verticaux turbulents , représentant les transports par les mouvements de petite échelle de la quantité de mouvement ( 福u w , 福v w ), de la chaleur ( 福w T ), et de l’humidité ( 福w q ). La mesure des fluctuations instantanées w , T , q , est réalisée grâce à une instrumentation spécifique de capteurs à réponse rapide, comme les anémomètres à fils chauds, les thermomètres à résistance de platine, ou les hygromètres «Lyman alpha», qui mesurent l’absorption radiative de la vapeur d’eau dans l’ultraviolet. Les résultats bruts sont ensuite corrélés et moyennés, et l’on a accès à la répartition spectrale des échelles qui assurent le transport. Pour les mesures en altitude, divers types de vecteurs sont utilisés, comme des mâts instrumentés, des avions équipés de centrales inertielles pour recaler les fluctuations mesurées du vent par rapport à un repère fixe, ou des ballons captifs.

La méthode la plus simple d’estimation des flux turbulents a été proposée par Ludwig Prandtl en 1925, sous le nom de théorie de la longueur de mélange ^{[cf. HYDRAULIQUE]}. Par une analogie avec la théorie cinétique des gaz, on postule que le flux 福w 﨏 de la quantité 﨏 peut s’exprimer sous la forme:

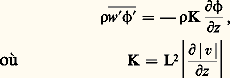
est un coefficient d’échange turbulent, et L une longueur caractéristique du déplacement turbulent, qui doit être déterminée empiriquement. Cette méthode est encore largement utilisée, sous des formes diverses. On lui préfère progressivement la méthode de l’«énergie turbulente», qui permet de mieux représenter les variations d’intensité du mélange turbulent sous l’influence de divers facteurs. Le coefficient d’échange turbulent s’écrit alors:

où e = (u ² + v ² + w ²)/2 est l’énergie cinétique turbulente moyenne par unité de masse et peut être calculée par son équation d’évolution où la production, le transport et la dissipation de turbulence sont représentés. Enfin, pour les applications les plus détaillées, la notion de coefficient d’échange turbulent doit elle-même être remise en cause: il arrive en effet que des transports significatifs de quantités comme la chaleur ou l’humidité se produisent à gradient nul (face=F0019 煉 﨏/ 煉z = 0), ou même à contre-gradient. Pour répondre à ces problèmes, des méthodes dites «d’ordre élevé» ont été développées: on utilise alors les équations d’évolution des flux turbulents eux-mêmes, en cherchant à modéliser les termes inconnus qui apparaissent dans ces équations (problème de la fermeture). Les échanges turbulents peuvent également être directement simulés par des modèles numériques de résolution très fine (50 m de maille): ces simulations tridimensionnelles ont apporté une meilleure confiance dans les autres méthodes d’estimation des flux, mais leur coût est encore prohibitif pour la plupart des applications.

Les principaux succès de l’étude de la turbulence dans la couche limite atmosphérique ont été apportés par la vérification expérimentale de plusieurs théories de similitude (cf. analyse et similitude DIMENSIONNELLES), permettant de regrouper dans un cadre unique des mesures d’origines très différentes, et de fournir un test contraignant aux méthodes de calcul des flux citées plus haut. Ainsi la théorie de similitude de la couche de surface , due à Monin et Obukhov, permet-elle de réaliser une prévision efficace des coefficients d’échange dans les premières dizaines de mètres de l’atmosphère, et donc de calculer les flux à l’aide de la seule connaissance des gradients des quantités moyennes. Son résultat est une généralisation de la «loi du mur» ou «vent logarithmique» ^{[cf. HYDRAULIQUE]}, qui prend en compte l’influence d’une stratification stable ou instable en densité. Il n’a en revanche pas été possible d’établir une telle loi pour l’ensemble de la couche limite atmosphérique, surtout en raison des phénomènes d’évolution temporelle dus au cycle diurne de la convection. Néanmoins, une approche fructueuse a été développée avec la théorie de similitude des couches de mélange convectif . On appelle couche de mélange convectif un régime particulier où, sous l’influence d’un mélange turbulent intensif causé par un réchauffement à la base, il n’apparaît plus de gradient vertical important de température, humidité, ou vent. De telles couches se rencontrent sur continent, en période diurne, quand le sol est chauffé par le rayonnement solaire, ou sur océan, où la convection est causée par l’évaporation intense. Elles sont surmontées d’une zone plus stable, ou «inversion de température», d’altitude variable, qui est alors le sommet de la couche limite, et est souvent le siège de variations verticales rapides des paramètres moyens. La structure de la turbulence dans de telles couches se prête à l’analyse de similitude, et peut être prévue à partir de la connaissance de quelques éléments, comme les flux au sol, et l’altitude de l’inversion. Celle-ci est déterminée par un équilibre dynamique entre les facteurs de grande échelle et le phénomène d’entraînement turbulent , par lequel les couches convectives incorporent en leur sein de l’air stable supérieur, et voient leur épaisseur augmenter au cours de la journée. La vitesse d’entraînement peut, dans les cas les plus simples, être prévue. On remplace alors le problème du calcul des flux en altitude par celui, plus simple, de la prévision de la hauteur de la couche turbulente.

Au-delà des problèmes strictement météorologiques, le développement des préoccupations environnementales a accru l’intérêt pour les recherches sur la couche limite atmosphérique, lieu des activités humaines. On réalise en effet de plus en plus qu’une bonne compréhension des phénomènes turbulents de la basse atmosphère est nécessaire pour l’étude de problèmes variés, comme la diffusion des polluants industriels, la formation des microclimats urbains, ou la protection contre les gelées et les brouillards.

• 1495, repris 1646; lat. turbulentia → turbulent

1 ♦ Agitation désordonnée, bruyante. Ils semblent « pleins de vigueur [les oiseaux], d'animation et de turbulence joyeuse » (Gautier).

2 ♦ Caractère d'une personne turbulente. ⇒ dissipation, pétulance, vivacité. « cette vivacité d'esprit gascon, cette aimable turbulence qui distingue ces Français du Nord » (Balzac).

3 ♦ (1956) Phys. Formation de tourbillons, dans un fluide. Turbulence d'un courant fluvial, d'une masse d'air. Étude des turbulences (en mécanique statistique). Nous entrons dans une zone de turbulences, attachez vos ceintures.

Synonymes :

Contraires :

Synonymes :

Contraires :

n. f.

d1./d Caractère d'une personne turbulente.

d2./d Agitation, désordre bruyant.

d3./d PHYS Irrégularité du mouvement d'un fluide (ayant un écoulement turbulent).

|| METEO Turbulence atmosphérique: agitation de l'atmosphère due aux variations thermiques, aux courants, au relief, etc.

⇒TURBULENCE, subst. fém.

1. Agitation bruyante et désordonnée. Un peu de l'innocence de leur enfance revenait chez ces femmes dans la turbulence d'ébats enfantins (E. DE GONCOURT, Élisa, 1877, p. 59). Mais le printemps est la saison de la délivrance et de l'espoir. On le fête, comme le fêtaient les anciens, avec allégresse, avec tout l'entrain et toute la turbulence du désir et de la joie de vivre (FARAL, Vie temps st Louis, 1942, p. 200).

2. Caractère d'une personne turbulente. Synon. agitation, dissipation, pétulance. Turbulence d'un élève, d'un enfant. Je note de l'assouplissement, de la discipline, de la mécanisation; certes, les rangs manœuvrent de mieux en mieux pour la conduite aux cabinets, pour la sortie du déjeuner. Les superbes leçons sur les inconvénients de la turbulence, de l'impétuosité, de la vivacité semblent avoir porté leurs fruits (FRAPIÉ, Maternelle, 1904, p. 161).

B. — PHYS. Turbulence (d'un fluide). ,,État d'un fluide qui est le siège de tourbillons`` (LAITIER 1969).

1. [Dans le mil. gazeux]

a) MÉTÉOR. ,,État de l'air affecté par de multiples mouvements verticaux convectifs ou non`` (GEORGE 1984). Turbulence thermique, dynamique; turbulence orageuse; zone de turbulences. Ces actions sont à rapporter au rôle de la turbulence dans le processus de formation des précipitations (MAURAIN, Météor., 1950, p. 136). [En partic., dans les voyages aériens] Zone de turbulence, traverser des turbulences. Il est recommandé aux aéronefs d'effectuer de plus des observations concernant (...) les fortes turbulences et les courants verticaux (MAURAIN, Météor., 1950, p. 151).

b) ASTRON. ,,Ensemble des phénomènes qui agitent un milieu traversé par le faisceau lumineux qui vient former l'image d'un astre`` (MULLER 1966). Peu affectée par la turbulence atmosphérique, la précision des pointes ne diminue que lentement avec la luminance des plages (Hist. gén. sc., t. 3, vol. 2, 1964, p. 543).

2. [Dans le mil. aqueux] HYDROL. ,,Caractère des écoulements affectés par des ondulations et des tourbillons`` (Géomorphol., 1979). Dans les mers à faibles marées surtout, la turbulence est le principal obstacle à la stratification de l'eau (J.-M. PÉRÈS, Vie océan, 1966, p. 88).

REM. Turbuler, verbe intrans., rare. Avoir un comportement turbulent. Synon. chahuter. Une foule épaisse coulait le long des baraques; des ventrées d'enfants turbulaient, soufflant dans des trompettes, barbouillés de pain d'épice, éveillés et morveux (HUYSMANS, Sœurs Vatard, 1879, p. 79).

Prononc. et Orth.:[]. Att. ds Ac. dep. 1762. Étymol. et Hist. 1. 1531 [éd.] « agitation bruyante » (J. DE VIGNAY, Mir. histor., XXVI, 44 ds GDF. Compl.); en partic. 1646 au plur. « troubles » (POUSSIN, Lett., 3 juin ds LITTRÉ); 2. 1728 « esprit de trouble » (VOLT., Henr., III, notes, ibid.); 3. 1935 « mouvement d'un fluide qui s'écoule en formant des tourbillons » (J. Phys. et Radium, p. 167^D). Empr. au b. lat. turbulentia « trouble, pertur-bation », dér. du lat. class. turbulentus, v. turbulent. Fréq. abs. littér.:121. Bbg. DARM. 1877, p. 184.

turbulence [tyʀbylɑ̃s] n. f.

ÉTYM. 1495; repris 1646; lat. turbulentia, de turbulentus. → Turbulent.

❖

1 a Vx. Trouble, tumulte collectif.

b Mod. Agitation désordonnée, bruyante (→ Exclure, cit. 12). || Une turbulence stérile (→ Actif, cit. 2).