Akademik

DIVISIBILITÉ

L’étude élémentaire de la divisibilité dans l’anneau Z des entiers relatifs résulte de l’existence de la division euclidienne qui entraîne que cet anneau est principal. Les propriétés générales des anneaux principaux sont exposées dans l’article ANNEAUX COMMUTATIFS, et nous nous contenterons ici d’énumérer les principaux résultats relatifs au cas particulier qui nous occupe ici.

L’étude plus fine et plus spécifique de l’anneau Z (nombre de diviseurs d’un nombre donné, somme de ces diviseurs, etc.) introduit des fonctions arithmétiques multiplicatives. Les indications qui suivent sont très élémentaires, mais il est important de noter qu’un grand nombre des résultats obtenus ont été généralisés aux corps de nombres algébriques; le dernier chapitre donne un aperçu de ces propriétés dans le cas des corps quadratiques, en renvoyant à l’article théorie des NOMBRES - Nombres algébriques pour l’exposé de la théorie sous sa forme contemporaine.

1. Propriétés élémentaires

L’anneau Z des entiers relatifs possède la propriété suivante de division euclidienne : si a et b sont deux entiers relatifs, b 0, il existe des entiers q et r déterminés de manière unique par les conditions:

q s’appelle le quotient de la division de a par b et b est le reste de cette division. Si le reste est nul, cela signifie qu’il existe un entier q tel que a = bq ; on dit alors que b divise a , ou que a est un multiple de b .

Dans ce qui suit, nous nous limiterons, sauf mention explicite du contraire, aux entiers positifs. On écrit b |a si b divise a . Cette relation de divisibilité est une relation d’ordre dans les entiers naturels; en effet, elle est réflexive car a | a , transitive car c | b et b | a entraînent c | a , antisymétrique car a | b et b | a entraînent a = b . Cet ordre n’est pas total car deux entiers a et b ne vérifient pas obligatoirement l’une des relations a | b ou b | a . Un nombre p 1 est dit premier s’il n’est divisible que par 1 et par lui-même.

Soient a et b deux entiers positifs; on montre ^{[cf. ANNEAUX COMMUTATIFS]} qu’il existe un diviseur commun d de a et de b tel que les diviseurs communs de a et de b soient exactement les diviseurs de d ; ce diviseur commun privilégié est appelé le plus grand commun diviseur (en abrégé P.G.C.D.) de a et de b et se note d = (a , b ). Si (a , b ) = 1, c’est-à-dire si le seul diviseur commun de a et de b est 1, on dit que a et b sont premiers entre eux . Une condition nécessaire et suffisante pour que a et b soient premiers entre eux est qu’il existe des entiers relatifs x et y tels que:

Ce résultat entraîne facilement le lemme de Gauss: si un entier c divise un produit ab et est premier avec a , alors il divise b . On en déduit le théorème fondamental de la décomposition en facteurs premiers : tout entier naturel a 礪 1 est décomposable, d’une manière unique, en un produit:

de nombres premiers p ¹, p ², ..., p ⁿ distincts; les exposants k ⁱ sont des entiers 閭 1. On peut, à partir de là, donner la règle d’obtention du P.G.C.D. de nombres ainsi décomposés: prendre les facteurs premiers communs avec les exposants les plus petits. On peut aussi bâtir sur ces décompositions la théorie du plus petit commun multiple (en abrégé P.P.C.M.) de deux nombres: prendre les facteurs premiers, communs ou non, avec leurs exposants les plus grands. Le P.P.C.M. ainsi introduit de a et b est un multiple commun m tel que les multiples communs de a et de b soient exactement les multiples de m ; il est relié au P.G.C.D. d de a et de b par la relation md = ab.

Indiquons enfin que les notions de P.G.C.D. et de P.P.C.M. s’étendent sans difficulté au cas de n entiers a ¹, a ², ..., a ⁿ .

2. Fonctions arithmétiques

Congruences

On se placera ici dans l’anneau Z des entiers relatifs. On dit que a est congru à b (modulo m ), ce qui s’écrit a 令 b (mod m ), lorsque m | (a 漣 b ). Cette congruence modulo m , pour m fixé, est une relation d’équivalence (réflexive, transitive, symétrique) et permet donc de faire une partition de Z en classes (ensemble quotient par cette équivalence). Chacune de ces classes est appelée classe résiduelle modulo m , et comprend un élément et un seul a compris entre 0 et (m 漣 1), soit 0 諒 a 諒 m 漣 1, tel que tout autre élément de la classe est égal à a + km. Si l’on désigne par [b ]^m la classe d’un entier b , il y a ainsi m classes, à savoir: [0]^m , [1]^m , [2]^m , ..., [m 漣 1]^m . On dit que m nombres b ¹, b ², ..., b ^m forment un système complet de résidus , modulo m , si ces nombres sont, deux à deux, non congrus modulo m ; ils correspondent donc aux m classes. La congruence modulo m étant stable dans l’addition et dans la multiplication, on peut munir l’ensemble des classes résiduelles des opérations de somme et de produit (avec [a ]^m + [b ]^m = [a + b ]^m et [a ]^m 憐 [b ]^m = [ab ]^m ). On obtient ainsi un anneau commutatif ^{[cf. ANNEAUX ET ALGÈBRES]}, dans lequel [ax ]^m = [ay ]^m entraîne [x ]^m = [y ]^m si a est premier à m ; dans le cas général, on n’aurait que [x ]^{m /d} = [y ]^{m /d} avec d = (a , m ). Un cas particulièrement intéressant est celui où m = p est premier; dans ce cas, en effet, l’anneau des classes résiduelles devient un corps, qu’on écrit en général Z/p Z ou Z/p . En effet, si [a ]^p 0, donc a non multiple de p , c’est-à-dire a premier avec p , on peut écrire ab + pc = 1, d’où [a ]^p [b ]^p = [1]^p , ce qui montre l’existence de 1 / [a ]^p = [b ]^p . Cela rejoint d’ailleurs une propriété classique: tout anneau fini sans diviseur de 0 est un corps. D’autre part, il est facile de voir que [a ]^m = [b ]^m équivaut à (a , m ) = (b , m ); on peut donc envisager les classes résiduelles premières à m qui forment, pour m donné, ce qu’on appelle un système réduit (par exemple, pour m = 18, les classes [1], [5], [7], [11], [13] et [17]). On dit alors qu’un ensemble d’entiers est un système réduit de résidus modulo m , si un et un seul de ces entiers appartient à chacune des classes d’un système réduit. Pour m = p premier, toutes les classes sauf [0] forment un système réduit, comprenant (p 漣 1) éléments. Dans le cas général de m quelconque, le nombre d’éléments d’un système réduit est égal à celui des nombres compris entre 1 et m et premiers à m . Ce nombre s’appelle l’indicateur d’Euler de m , désigné par 﨏(m ), et l’on peut établir les conditions nécessaires et suffisantes suivantes pour qu’un ensemble de nombres soit un système réduit de résidus modulo m : ce système comprend 﨏(m ) éléments; ces éléments sont deux à deux non congrus modulo m ; chaque élément est premier à m . Il est alors évident que, si l’on multiplie chacun de ses éléments par un même facteur premier à m , on transforme un système réduit de résidus en un système réduit.

Fonctions arithmétiques classiques

La fonction 﨏 d’Euler est une fonction arithmétique multiplicative ; on appelle ainsi toute fonction f définie sur les entiers naturels, et telle que f (ab ) = f (a ) f (b ) lorsque (a , b ) = 1. On établit sur les fonctions arithmétiques multiplicatives l’important théorème suivant: si f est arithmétique multiplicative et si l’on pose:

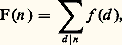
alors F est aussi multiplicative, et réciproquement.

De plus, on a:

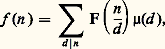
où:

Cette fonction 猪 s’appelle fonction de Möbius ; elle est aussi multiplicative. La relation de réciprocité liant f à F, grâce à cette fonction de Möbius, reste d’ailleurs valable dans le cas de fonctions non multiplicatives; elle s’établit par simple calcul, et fournit la démonstration la plus simple du fait que f est multiplicative si F l’est. L’implication en sens contraire est beaucoup plus simple à établir; elle résulte de ce que tout diviseur d’un produit de deux nombres premiers entre eux est le produit d’un diviseur de l’un par un diviseur de l’autre.

On établit donc que la fonction 﨏 d’Euler est arithmétiquement multiplicative, soit en la mettant sous la forme:

car c’est:

où les p ⁱ sont les facteurs premiers de m ; soit aussi en considérant les nombres de la forme ax + by qui sont premiers à ab (système réduit de résidus, modulo ab ).

Si l’on envisage alors:

on a une fonction multiplicative qui, par simple calcul, donne 淋(p size=1^見) = p size=1^見, donc 淋(m ) = m pour tout m . Cela établit la formule classique:

qui peut aussi se démontrer en rangeant 1, 2, 3, ..., m en classes C^d , comprenant les nombres dont le P.G.C.D. avec m est d ; il y a 﨏(m /d ) nombres dans C^d , d’où la formule précédente, par simple décompte.

La formule de réciprocité de Möbius, appliquée à:

Deux autres fonctions multiplicatives sont classiquement attachées à la fonction 﨏 d’Euler; il s’agit de 精(n ) = nombre des diviseurs positifs de n (1 et n compris) et 靖(n ) = somme de ces diviseurs. La multiplicativité de ces deux fonctions découle encore de ce que, si a et b sont premiers entre eux, tout diviseur de ab est le produit d’un diviseur de a par un diviseur de b . Comme:

À noter la relation:

où la quantité entre crochets représente ici la partie entière de k /n .

Nombres parfaits

On appelle nombre parfait un nombre tel que 靖(n ) = 2n , et on a établi que tout nombre parfait pair s’écrit sous la forme:

avec p et (2^p 漣 1) premiers (Euclide avait déjà étudié sous cette forme les nombres parfaits). On ne sait pas, actuellement, s’il y a ou non des nombres parfaits impairs. Les nombres parfaits pairs sont donc liés aux nombres premiers de la forme 2^p 漣 1. Ces nombres sont appelés nombres de Mersenne (Mersenne affirma en 1644 que, jusqu’à p = 257, 2^p 漣 1 était premier seulement si p = 2, 3, 5, 7, 13, 17, 19, 31, 67, 127 et 257). On a établi, depuis, que cette liste contenait des erreurs et des omissions: jusqu’à 5 000, (2^p 漣 1) est premier pour p = 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127, 521, 607, 1 279, 2 203, 2 281, 3 217, 4 253 et 4 423. Fermat, de son côté, avait conjecturé que les nombres de Fermat :

étaient tous premiers. Euler en 1732 établit que ⁵ était composé (divisible par 641), Legendre en 1780 établit que ⁶ est divisible par 274 177. On a établi, depuis, que Fⁿ est non premier pour 7 諒n 諒 16 et n = 18, 23, 36, 38, 39, 55, 63, 73, ...; et on ne connaît explicitement aucun Fⁿ premier pour n 礪 4. Les nombres de Fermat premiers jouent un rôle essentiel dans la recherche des polygones réguliers de m côtés que l’on peut construire avec la règle et le compas (Gauss, âgé de dix-sept ans, établit qu’une condition nécessaire et suffisante pour que cette construction soit possible est que m soit un produit de nombres de Fermat premiers distincts).

3. Théorèmes classiques

Théorème d’Euler-Fermat

Euler établit, en 1760, le théorème d’Euler-Fermat, suivant lequel, si m est entier naturel, et (a , m ) = 1, on a:

En effet, un système réduit de résidus modulo m , soit r ¹, r ², ..., r size=1^{﨏(m )} est transformé, on l’a vu, en un système réduit par multiplication par a ; donc ar ¹, ar ², ..., ar size=1^{﨏(m )} sont, modulo m , égaux à une permutation de r ¹, r ², ..., r size=1^{﨏(m )} d’où le produit:

que l’on peut simplifier par r ¹ r ² ... r 﨏^(m) premiers à m. D’où la formule d’Euler-Fermat. Fermat avait établi en 1736 ce théorème dans le cas particulier de m = p premier. Il s’agit du «petit théorème de Fermat», suivant lequel:

si a n’est pas multiple de p . On l’écrit, sans condition sur a , a ^p 令 a (mod p ). On remarquera que la réciproque de ce théorème n’a pas lieu (par exemple m = 561 = 3 憐 11 憐 17 vérifie, pour tout a premier à m , a ⁵⁶⁰ 令 1). On a d’autre part établi (Beeger en 1951) qu’il existe une infinité d’entiers n pairs tels que 2ⁿ 漣 2 est divisible par n (le plus petit de ces nombres étant 161 038).

Théorème de Wilson

Le théorème de Wilson énonce que:

pour tout p premier (théorème publié en 1770 par Waring et démontré par Lagrange en 1771). Supposant p impair et développant:

Lagrange obtient, après avoir multiplié par x puis changé x en (x 漣 1), une identité permettant d’établir que p |A¹, p |A², ..., p |A^p-2 et (p 漣 1) A^p-1 令 1 (mod p ). On a donc A^p-1 令 漣 1 (mod p ), ce qui établit le théorème, car A^p-1 = (p 漣 1)!. On a de plus:

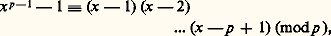
ce qui, pour x premier à p , donne le petit théorème de Fermat. On verra une autre démonstration du théorème de Wilson, dans le paragraphe des résidus quadratiques.

Racines primitives

La notion de racine primitive modulo m , est liée à la formule d’Euler:

Soit en effet k le plus petit exposant pour lequel a ^p 令 1 (mod m ). On dit que a appartient à l’exposant k (mod m ), ou que k est l’ordre de a , modulo m . Il s’ensuit que k divise tout x tel que a ^x 令 1 (mod m ); en particulier, k | 﨏 (m ), et on dit que a est une racine primitive modulo m si l’ordre de a est 﨏(m ), c’est-à-dire si 﨏(m ) est effectivement le plus petit exposant pour lequel a ^p 令 1 (mod m ). Cette définition montre que tout entier congru, modulo m , à une racine primitive, en est également une. Ces racines primitives ont l’importante propriété que, pour chacune d’elle, a par exemple, les nombres a , a ², a ³, ..., a size=1^{﨏(m )} forment un système réduit de résidus. On démontre que tout p premier possède des racines primitives; il y en a exactement 﨏(p 漣 1) distinctes entre elles, modulo p. Cela découle d’un théorème assez surprenant suivant lequel, si p est premier, et d |(p 漣 1), il y a exactement 﨏 (d ) nombres non congrus 2 à 2 et dont l’ordre est d (modulo p ); le nombre des nombres d’ordre d (modulo p ) ne dépend donc pas de p , dès que d divise (p 漣 1). Pour l’existence des racines primitives modulo m , avec m non premier, l’étude, plus délicate, fut faite par Gauss, qui établit que ces racines primitives n’existent que si m = 2, 4 ou p ^k ou 2p ^k (p premier impair quelconque).

4. Résidus quadratiques

Résidus et non-résidus

Un nombre a premier à m est dit résidu quadratique de m , si x ² 令 a (mod m ) a des solutions entières en x ; sinon a est dit non-résidu quadratique (avec toujours la condition a premier à m ). Dans le cas où m = p premier, il est facile de voir qu’il existe, modulo p , (p 漣 1)/2 résidus quadratiques et (p 漣 1)/2 non-résidus; en effet, 1², 2², ..., (p 漣 1)² donnent, modulo p , (p 漣 1)/2 classes résiduelles différentes; car (p 漣 q )² 令 q ² et a ² 漣 b ² = (a 漣 b ) (a + b ) 令 0 (mod p ) si a et b sont au plus égaux à (p 漣 1)/2. Par exemple, pour p = 11, on a les résidus quadratiques 1, 3, 4, 5 et 9. On peut établir aisément, pour m quelconque, que le produit de deux résidus quadratiques de m est un résidu; car x ² 令 a et y ² 令 b entraîne (xy )² 令 ab (mod m ). Dans le cas où m = p premier, le produit d’un résidu par un non-résidu est un non-résidu et le produit de deux non-résidus est un résidu; il suffit pour cela d’envisager a , 2 a , 3 a , ..., (p 漣 1)a , qui sont non congrus modulo p , donc forment un système complet (mod p ). Il y a donc (p 漣 1)/2 résidus et (p 漣 1)/2 non-résidus, quel que soit a premier à p , et, si a est résidu, les (p 漣 1)/2 résidus proviennent du produit par a des résidus quadratiques de p , donc les (p 漣 1)/2 non-résidus correspondent aux produits de a par les non-résidus de p. Si a est non-résidu, les (p 漣 1)/2 non-résidus proviennent donc du produit de a par les résidus quadratiques de p , donc les (p 漣 1)/2 résidus correspondent aux produits de a par les non-résidus de p . Pour m quelconque, cependant, on peut avoir le produit de deux non-résidus qui soit un non-résidu: par exemple, pour m = 45, les résidus quadratiques sont 1, 4, 16, 19, 31, 34, et 2 憐 7 = 14. Un critère d’Euler établit que, pour p premier différent de 2, a est résidu ou non-résidu quadratique de p suivant que, respectivement,

on ne peut avoir que l’une ou l’autre de ces congruences puisque a ^p-1 令 1 (mod p ). On peut, à partir de ce critère, retrouver les théorèmes concernant les produits de résidus ou non-résidus (mod p ).

Loi de réciprocité

Legendre a introduit un symbole qui porte son nom: pour p premier,

si a est résidu;

si a est un non-résidu. On a donc:

Ce symbole permet d’exprimer un important théorème connu sous le nom de loi de réciprocité quadratique . Cette loi fut prouvée par Euler en 1783, retrouvée par Legendre en 1785 et mise au point par Gauss en 1808; elle s’écrit, pour deux premiers impairs distincts p et q , sous la forme:

En d’autres termes les congruences x ² 令 p (mod q ) et y ² 令 q (mod p ) sont résolubles ensemble, ou non, sauf si p 令 q 令 3 (mod 4), auquel cas une et une seule de ces équations est résoluble. Le symbole de Legendre a été étendu par Jacobi, qui définit

les nombres premiers p ⁱ étant distincts ou non. Ce symbole, toutefois, a l’inconvénient d’être égal à + 1 sans que a soit toujours résidu quadratique modulo p ¹ p ² ... p ⁿ ; par exemple:

vaut toujours + 1. On peut cependant établir, pour a et b premiers entre eux, que

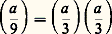
entraîne que a est non-résidu quadratique modulo b . Signalons enfin que le théorème de Wilson: (p 漣 1)! 令 漣 1 (mod p ), établi antérieurement, se démontre à partir des résidus: pour p premier impair et pour a non multiple de p , on peut établir que:

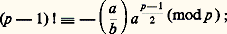
il suffit, pour cela, d’associer les couples x et (p 漣 x ) et de voir que, deux à deux, on a x x 令 a (mod p ) ou bien, si a est résidu, x ¹² 令 a et (p 漣 x ¹)x ¹ 令 漣 a (modp ) et x x 令 a (mod p ) pour les autres. Les résidus quadratiques sont utilisés en particulier dans la théorie des corps quadratiques, dans la factorisation des nombres (par exemple, si N = x ² + ky ², avec x et y premiers entre eux, 漣 k doit être résidu quadratique de tous les facteurs premiers de N, ce qui facilite la factorisation), et aussi dans la recherche des carrés parfaits dans le corps Q^p des nombres p -adiques. À côté de la recherche directe, par développements de Hensel, l’introduction du symbole de Hilbert ( 見, 廓), égal à + 1 ou 漣 1 suivant que 見x ² + 廓y ² 漣 z ² = 0 est résoluble ou non dans Q^p , conduit à la caractérisation des carrés 見 par le fait que ( 見, 廓) = 1 pour tout 廓.

5. Divisibilité dans les corps quadratiques

On ne donnera ici qu’un aperçu de la théorie de la divisibilité dans les corps quadratiques. Si l’on considère les nombres de la forme:

où d est entier non carré parfait, et u , v , w entiers relatifs (avec w 閭 1), on définit un corps, appelé corps quadratique Q (face=F0019 連d ). Dans ce corps, on appelle entiers les éléments qui vérifient une équation du type 見² + a ¹ 見 + a ² = 0, a ¹ et a ² étant des entiers; et on démontre que ces entiers sont donnés par les formules:

Ces entiers forment un sous-anneau de Q (face=F0019 連d ), et on peut définir dans cet anneau la divisibilité, compliquée par le fait qu’il existe d’autres unités que + 1 ou 漣 1. Une unité quadratique est en effet racine d’une équation (cf. équations DIOPHANTIENNES):

Il y a une infinité d’unités dans Q (face=F0019 連d ) pour d 閭 2 et, pour d 諒 漣 1, il n’y en a pas d’autre possible que 1, 漣 1; i , 漣 i et les racines troisièmes de l’unité j , j ², 漣 j et 漣 j ². Une unité divise tout entier; on définira donc les nombres premiers comme étant ceux qui ne sont divisibles que par eux ou par les unités du corps. De même, a et b seront dits premiers entre eux si leurs seuls diviseurs communs sont les unités; on écrit encore (a , b ) = 1 mais c’est un symbole car 1 n’est plus le P.G.C.D. au sens ordinaire. Sans entrer dans le détail, signalons qu’alors le théorème de Gauss (a |bc et (a , b ) = 1 entraînent a |c ) peut avoir lieu, ou ne pas avoir lieu, suivant d . Lorsque ce théorème a lieu, Q (face=F0019 連d ) est appelé corps quadratique simple ; en découle une décomposition unique en facteurs premiers (à des facteurs unités près). Par exemple, il en est ainsi pour d = 漣 1, d = 2, d = 漣 3, mais pas pour d = 漣 5 ou d = 10 (on a par exemple:

et on vérifie qu’il n’y a pas d’unités permettant de passer d’une décomposition à l’autre). Les seuls cas quadratiques simples, pour d 麗 0, sont les cas où 漣 d = 1, 2, 3, 7, 11, 19, 43, 67, 163 (résultat de Stark et Baker en 1966; avant eux on avait établi qu’il en existait peut-être encore un, avec 漣 d 礪 5 憐 10⁹). Une autre notion peut s’étendre à Q (face=F0019 連d ); il s’agit de la division euclidienne, qui fait intervenir les normes des nombres quadratiques, soit N ( 見) = 見 見 (où 見 est le conjugué de 見). Q (face=F0019 連d ) est dit euclidien si, pour tout 見¹ et 見² entiers, on peut écrire 見¹ = 廓見² + 塚 avec N( 塚) 麗 N( 見²). Q (face=F0019 連d ) «euclidien» entraîne évidemment Q (face=F0019 連d ) «simple», mais pas réciproquement. On a démontré que les seuls cas euclidiens correspondent à d = 漣 11, 漣 7, 漣 3, 漣 2, 漣 1, 2, 3, 5, 6, 7, 11, 13, 17, 19, 21, 29, 33, 37, 41, 57 et 73. Le cas d = 漣 1 est le cas, bien connu, des entiers de Gauss a + bi où a et b sont des entiers relatifs ordinaires.

• XV^e; de divisible

n. f. MATH Propriété d'un nombre divisible.

⇒DIVISIBILITÉ, subst. fém.

Qualité de ce qui peut être divisé; ,,propriété qu'a un tout d'être décomposable soit matériellement, soit idéalement, en un certain nombre de parties`` (LAL. 1968). La divisibilité des corps, de la matière, du temps; divisibilité territoriale. La divisibilité, la possibilité d'être divisé, résulte (...) inévitablement de la propriété d'être étendu (DESTUTT DE TR., Idéol. 1, 1801, p. 177). Le gage est indivisible nonobstant la divisibilité de la dette entre les héritiers du débiteur ou ceux du créancier (Code civil, 1804, art. 3, p. 374). On ne peut lutter contre la mer qu'en tirant parti de la divisibilité de cette force (HUGO, Travaill. mer, 1866, p. 318).

— Spéc., MATH. Propriété d'un nombre de pouvoir être divisé exactement par un autre. La divisibilité par 9, je l'ai apprise si longtemps que j'ai fini par la retenir (COLETTE, Cl. école, 1900, p. 209) :

• Après Gauss, le fondateur de la théorie [des nombres algébriques], tout l'effort du XIX^e siècle avait porté sur l'étude des lois de la divisibilité des entiers algébriques d'un même corps de nombre donné; ...

Les Gds courants de la pensée mathématique, 1948, p. 293.

Prononc. et Orth. :[divizibilite]. Ds Ac. 1718-1932. Étymol. et Hist. Fin XIV^e-début XV^e s. (Catholicon, B.N. 1. 17881 ds GDF. Compl.). Dér. de divisible; suff. -ité. Fréq. abs. littér. :35.

divisibilité [divizibilite] n. f.

ÉTYM. Fin XIV^e; de divisible.

❖

♦ Sc. Caractère de ce qui peut être divisé. || La divisibilité de la matière, de l'espace. || Le mercure (cit. 3) est d'une divisibilité prodigieuse. Math. || Caractères de divisibilité, par lesquels on peut reconnaître qu'un nombre est divisible par un autre.