- СДВИГ
-
простейшая деформация тела, вызываемая касат. напряжениями t. С. явл. мерой искажения углов элементарных параллелепипедов (рис.),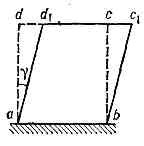 на к-рые можно разбить однородное тв. тело, — прямоугольный параллелепипед abcd превращается в косоугольный abc1d1. Перемещение d1d наз. абсолютным С. грани dc относительно грани ad; угол g наз. углом С., а tgg — относительным С. Ввиду малости g можно считать tgg=g. Если по граням параллелепипеда действуют только касат. напряжения т, С. наз. чистым. В пределах упругости для изотропного материала относит. С. связан с Гука законом: t=Сg, где G — модуль С. для данного материала (см. МОДУЛИ УПРУГОСТИ). На практике С. часто сопутствует растяжению и сжатию, когда одновременно с нормальными возникают и касат. напряжения.
на к-рые можно разбить однородное тв. тело, — прямоугольный параллелепипед abcd превращается в косоугольный abc1d1. Перемещение d1d наз. абсолютным С. грани dc относительно грани ad; угол g наз. углом С., а tgg — относительным С. Ввиду малости g можно считать tgg=g. Если по граням параллелепипеда действуют только касат. напряжения т, С. наз. чистым. В пределах упругости для изотропного материала относит. С. связан с Гука законом: t=Сg, где G — модуль С. для данного материала (см. МОДУЛИ УПРУГОСТИ). На практике С. часто сопутствует растяжению и сжатию, когда одновременно с нормальными возникают и касат. напряжения.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- СДВИГ
-
- простейшая деформация тела, вызываемая касат. напряжениямит. С. выражается в искажении углов элементарных параллелепипедов (рис.1), из к-рых можно считать составленным однородное тело; прямоугольныйпараллелепипед abcd превращается в косоугольный
относительно грани ad; угол 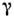 наз. углом С., а
наз. углом С., а 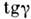 -относительным С. Ввиду малости
-относительным С. Ввиду малости 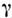 можно считать
можно считать 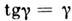 , т. е. что относительный С. равен
, т. е. что относительный С. равен 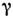 .В пределах упругости для изотропного материала относительный С. связанс
.В пределах упругости для изотропного материала относительный С. связанс  законом Гуна:
законом Гуна: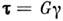 , где G - модуль С. для данного материала (см. Модули упругости). С. всегда сопутствует растяжению, сжатию и изгибу, т. к. во всех этихслучаях одновременно с нормальными возникают и касат. напряжения.
, где G - модуль С. для данного материала (см. Модули упругости). С. всегда сопутствует растяжению, сжатию и изгибу, т. к. во всех этихслучаях одновременно с нормальными возникают и касат. напряжения.Напряжённое состояние, при к-ром 2 гл. напряжения равны по величинеи обратны по знаку, наз. чистым С. В этом случае (рис. 2) нормальное напряжениена площадках, образующих с направлением сил углы 45°, равно нулю, а касат. напряжения достигают макс. величины. Т. о., элементарный куб abcd находитсяв условиях чистого С., причём касат. напряжения, действующие по его граням, равны между собой. Чистый С. имеет место при кручении. Потенциальнаяэнергия С. для первоначально прямоугольного параллелепипеда длиной . при площади основания S и сдвигающей силе Р может бытьпредставлена ф-лами:
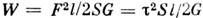 , а уд. потенциальная энергия
, а уд. потенциальная энергия 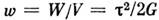 ,где V = lS - объём параллелепипеда.
,где V = lS - объём параллелепипеда.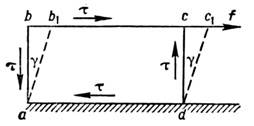
Рис. 1.
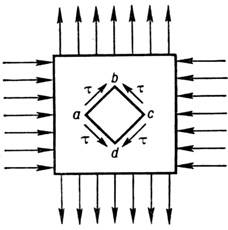
Рис 2.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.