Akademik

ALGORITHMIQUE

L’objet de l’algorithmique est la conception, l’évaluation et l’optimisation des méthodes de calcul en mathématiques et en informatique. Un algorithme consiste en la spécification d’un schéma de calcul, sous forme d’une suite d’opérations élémentaires obéissant à un enchaînement déterminé.

Le terme d’algorithme tire lui-même son origine du nom du mathématicien persan Al Khw rizm 稜 (env. 820) dont le traité d’arithmétique servit à transmettre à l’Occident les règles de calcul sur la représentation décimale des nombres antérieurement découvertes par les mathématiciens de l’Inde.

Divers algorithmes ont été en fait connus dès l’Antiquité dans le domaine de l’arithmétique ou de la géométrie, parmi lesquels, notamment:

– les règles de calcul de longueur d’arcs et de surfaces des civilisations égyptienne et grecque;

– plusieurs méthodes de résolution d’équations en nombres entiers, à la suite des travaux de Diophante d’Alexandrie au IV^e siècle;

– l’algorithme d’Euclide (env. 300 av. J.-C.) qui permet le calcul du plus grand commun diviseur de deux nombres;

– le schéma de calcul du nombre 神 dû à Archimède.

Ensuite ont été étudiées les méthodes numériques de résolution d’équations algébriques (algorithme de Newton, méthode d’élimination de Gauss), puis d’équations différentielles. Enfin, l’avènement de calculateurs électroniques, à l’issue de la Seconde Guerre mondiale, a entraîné un renouvellement complet de l’algorithmique, appliquée désormais soit à des problèmes de taille bien supérieure à celle des problèmes traités manuellement (d’où la nécessité de méthodes nouvelles), soit surtout à des types de problèmes nouveaux, comme le tri, la recherche rapide d’informations non numériques (base de données) ou l’optimisation combinatoire.

1. L’exemple du calcul de size=5神

La question du calcul du nombre 神 = 3,141 592 6... (rapport de la circonférence au diamètre d’un cercle), étudiée dès l’Antiquité, est caractéristique des problèmes généraux rencontrés en algorithmique.

Historiquement, une fois reconnue l’existence d’un rapport constant entre circonférence et diamètre d’un cercle, la première approche a consisté à déterminer le nombre 神 par des mesures physiques: l’on obtient de la sorte des valeurs approchées du type 3 (comme dans la Bible), 3 et 1/7 ou 3 et 1/8. Cependant à ce stade, rien n’indique que 神 soit un nombre calculable , c’est-à-dire qu’une méthode existe qui permette de le déterminer avec une précision arbitrairement grande. Il revient à Archimède (287-212 av. J.-C.) d’avoir le premier proposé un algorithme de calcul de 神.

Le principe de l’algorithme d’Archimède est le suivant: Soit p ⁿ le périmètre d’un polygone régulier de n côtés inscrit dans un cercle de rayon 1/2. Archimède observe que:

et il évalue la limite au moyen de la suite p ⁶, p ¹², p ²⁴, p ⁴⁸... obtenue par doublements successifs du nombre de côtés. Soit u ⁿ = (1/n ) p ⁿ la longueur du côté d’un n -gone; de propriétés géométriques élémentaires se déduit la récurrence:

laquelle se vérifie trigonométriquement grâce aux relations:

et à la formule générale:

Partant des valeurs connues pour l’hexagone:

on calcule de proche en proche par (1) les valeurs p ⁶, p ¹², p ²⁴... par une succession d’opérations algébriques. Les premières valeurs des approximations 神^m = p ^6.2m ainsi obtenues sont présentées dans le tableau 1.

Dans un langage de spécification d’algorithmes ^{[cf. PROGRAMMATION]}, l’algorithme de calcul de 神^m s’exprime sous la forme:

Cela correspond à une spécification complète d’un enchaînement d’opérations élémentaires (+, 漣, 憐, ÷, 連) sur les nombres réels.

Pour un calcul effectif de 神, on doit de plus déterminer la relation entre la valeur de m choisie et l’écart | 神 漣 神^m | ainsi que la précision nécessaire des calculs intermédiaires.

On observe par exemple que la formule (1) met en jeu la différence de deux quantités très voisines: 1 et 連1 漣 u ²ⁿ . Une erreur relative, même faible, sur u ⁿ entraîne donc une erreur beaucoup plus importante sur u ²ⁿ . De tels phénomènes sont courants en analyse numérique (cf. CALCUL NUMÉRIQUE). On obtient des formules qui ne présentent pas ce caractère de difficulté en multipliant le radical:

par sa quantité conjuguée. Il vient, après simplification, la récurrence:

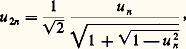
qui possède des propriétés de «stabilité» numérique (insensibilité aux erreurs d’arrondi) bien supérieures aux formules initiales. Un tel procédé a été en substance découvert par Viète (1593) et lui a permis de déterminer les sept premières décimales de 神.

Un algorithme d’un type très différent a été proposé par John Machin (1680-1752) et repose sur la formule:

qui se vérifie au moyen de formules d’additions trigonométriques. La fonction Arc tg x est calculable par le développement:

L’algorithme de Machin consiste donc à calculer les approximations successives 神 ^m de 神 données par:

où:

On observe sur le tableau 1 que la convergence de 神 ^m vers 神 est environ deux fois plus rapide que la convergence de 神^m vers 神. Le calcul, de surcroît, ne nécessite pas l’extraction de racines carrées. L’algorithme résumé par les formules (4) et (5) pourrait être spécifié sous forme de programme analogue à (3). Il permit à J. Machin de déterminer les cent premières décimales de 神.

Plus récemment, des formules d’addition du type de la formule de Machin ont servi de base au calcul sur ordinateur de plusieurs centaines de milliers de décimales de 神: en 1966, Guilloud et Filliatre ont ainsi déterminé les cinq cent mille premières décimales de 神.

Enfin, la méthode de calcul de 神 qui possède de bonnes propriétés de convergence a été trouvée par Salamin. Une analyse détaillée a montré que cette méthode rendait possible le calcul de plusieurs millions de décimales de 神 en quelques heures de calcul d’un ordinateur de grosse capacité, au prix cependant d’un effort de programmation important lié à la nécessité de procédures de multiplication générale et d’extraction de racine carrée (de telles procédures sont présentées au chapitre 2).

Dans l’algorithme de Salamin, le m -ième approximant de 神 s’obtient par la formule:

où les a ⁿ , b ⁿ sont calculés par les récurrences:

avec:

La justification de l’algorithme de Salamin repose sur la théorie des intégrales elliptiques. La convergence de 神 ^m vers 神 est extrêmement rapide (tabl. 1).

L’exemple de ce problème classique illustre les deux critères de l’intérêt d’un algorithme nouveau: soit permettre la résolution d’un problème pour lequel aucun schéma de calcul n’était préalablement connu (algorithme d’Archimède), soit permettre un calcul beaucoup plus rapide qu’il n’était possible au moyen des algorithmes précédemment connus.

La classification des diverses solutions algorithmiques à un problème donné s’effectue ainsi sur la base de leur complexité mesurée en nombre d’opérations élémentaires nécessaires à leur exécution. Pour les trois algorithmes précédents, une analyse montre par exemple que le nombre d’itérations nécessaires à l’obtention de 神 avec une précision de 10^-n vaut approximativement:

On simplifie généralement les descriptions de complexité d’algorithmes en ne retenant que les ordres de grandeur correspondants. On utilise pour cela la notation de Landau (cf. calculs ASYMPTOTIQUES), qui consiste à écrire:

pour une certaine constante C. Avec cette notation les équations (8) se résument en:

2. Algorithmes arithmétiques

La catégorie des algorithmes arithmétiques inclut les algorithmes des opérations fondamentales sur les entiers et les polynômes: dans le cas d’entiers de grande taille – de polynômes de degré élevé – des méthodes récursives ou fondées sur la transformation de Fourier discrète conduisent à des gains importants. Les algorithmes de factorisation et de test de primalité, liés à la théorie des nombres, ont permis de construire des systèmes de codage nouveaux (systèmes à clefs publiques).

Addition et multiplication classiques

À tout vecteur binaire a = (a ⁰, a ¹, ..., a ^{n -1}), où a ⁱ 捻0, 1, se trouve associé l’entier:

également noté a et dont le vecteur constitue la représentation binaire de longueur (taille) n . Étant donné deux entiers a , b , donnés par leurs représentations de longueur n , un problème de base consiste à déterminer la somme et le produit:

sous forme de représentations binaires de longueur n + 1 et 2n respectivement. L’algorithme classique calcule les bits s ⁱ de s par les relations:

où r ⁱ représente la retenue entrante correspondant à la position i .

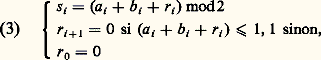
Le produit p correspond dans l’algorithme classique au développement:

L’évaluation de (4) correspond seulement à n additions d’entiers de longueur 2 n , puisque les multiplications par 2ⁱ s’obtiennent en représentation binaire par simple décalage.

La mesure naturelle de complexité de ces algorithmes est le nombre d’opérations booléennes élémentaires effectuées. Les complexités respectives de l’addition et de la multiplication selon ces méthodes sont aussi respectivement:

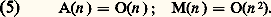
Méthodes récursives

Soit à évaluer le produit de deux nombres x et y de longueur n = 2m donnés sous la forme:

Le produit xy vaut:

et, sous cette forme, le calcul nécessite quatre multiplications de nombres de taille m . On peut se ramener au calcul de trois produits seulements:

en observant la relation:

L’utilisation répétée (pour le calcul des produits P¹, P², P³) de cette décomposition, qui ramène une multiplication d’entiers de taille 2m à trois multiplications en longueur m , conduit à un algorithme récursif dont le coût vérifie ainsi la récurrence:

(les termes en O(m ) représentent le coût des additions). La solution de (10) est:

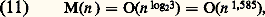
Ce qui représente par rapport à (5) un gain substantiel lorsque n est grand.

Une méthode analogue s’applique au produit de polynômes (en remplaçant dans les équations (5) à (8), le nombre 2 par l’indéterminée x ) et permet également de calculer le produit de deux polynômes de degré n en O(n ^1,585) opérations élémentaires sur les coefficients.

Il a été montré également par Strassen que le produit de deux matrices de dimension (2m ) 憐 (2m ) se ramène au produit de sept matrices de dimension m 憐 m . L’utilisation récursive de cette réduction conduit à un algorithme de multiplication matricielle pour des matrices de dimension n dont la complexité en nombre d’opérations sur les coefficients est égale à:

Les méthodes de conception récursives de ce type sont susceptibles d’applications très nombreuses, aussi bien dans le domaine des algorithmes arithmétiques (le calcul de transformées de Fourier), que dans celui du traitement de données non numériques.

Algorithme de Newton

L’algorithme de Newton (cf. histoire du CALCUL NUMÉRIQUE) consiste à approcher une solution de l’équation:

par la récurrence:

la valeur initiale x ⁰ étant choisie suffisamment proche de la racine x de (12).

L’application de cette méthode aux fonctions:

conduit à deux suites récurrentes:

Sous des conditions très larges sur les valeurs initiales y ⁰ et z ⁰, y ⁿ et z ⁿ convergent vers les zéros de g et h respectivement, soit:

Les relations (14) et (15) ramènent donc le calcul de l’inverse et de la racine carrée d’un entier aux seules opérations d’addition et de multiplication. Le caractère très rapide de la convergence (convergence quadratique) de l’algorithme de Newton entraîne que les coûts I(n ) et R(n ) de calcul d’inverse et d’extraction de racine carrée avec une précision de n bits sont du même ordre que le temps de la multiplication.

Transformation de Fourier discrète

La transformation de Fourier discrète (TFD) d’ordre n est une application Tⁿ de Cⁿ dans Cⁿ :

définie par:

諸ⁿ = exp(2i 神/n ) étant une racine n -ième de l’unité. Il s’agit donc d’un analogue discret de la transformation de Fourier classique. La transformation inverse (TFDI) s’exprime par les formules analogues:

Supposons n pair; séparant les contributions des composantes d’indice pair et impair de x , on obtient:

Les formules (17) montrent que le calcul de Tⁿ (x ¹, x ², ...) se décompose en celui de T^{n /2} (x ⁰, x ², x ⁴, ...) et de T^{n /2} (x ¹, x ³, x ⁵, ...) suivi de 2n opérations d’addition et de multiplication complexes. Si n est une puissance de 2, la même décomposition peut être appliquée récursivement: chaque TFD d’ordre n /2 se ramène au calcul de deux TFD d’odre n /4 ...

Ce principe est à la base de l’algorithme dit de transformée de Fourier (discrète) rapide (TFR) explicité par Cooley et Tuckey en 1965. La complexité du calcul de Tⁿ par l’algorithme TFR mesurée en nombre d’opérations élémentaires sur R ou C vérifie ainsi la récurrence:

dont la solution est:

L’algorithme TFR représente une réduction de complexité importante, puisqu’un calcul direct de (16) correspond à un nombre d’opérations élémentaires en O(n ²). Il possède de nombreuses applications au calcul numérique de transformées de Fourier et de produits de convolution en traitement du signal et en traitement d’images.

L’intérêt de la TFR pour les algorithmes arithmétiques provient de ce que la TFD transforme les produits de convolution de vecteurs en produits composante par composante. On peut ainsi obtenir le produit de deux polynômes de degré inférieur à n /2 de la manière suivante:

(a ) calculer les TFR d’ordre n des vecteurs des coefficients;

(b ) effectuer le produit composante par composante des transformées;

(c ) appliquer à ce résultat une TFD inverse calculée par l’algorithme TFR.

La complexité, en nombre d’opérations sur R ou C, de l’algorithme obtenu vérifie donc la relation:

Schönhage et Strassen ont montré en 1971 que l’utilisation de la TFR permet de calculer le produit de deux entiers de n bits en un nombre d’opérations booléennes élémentaires égal à:

Cependant, la complexité de la mise en œuvre de cet algorithme n’en rend l’utilisation avantageuse que pour des valeurs de n relativement grandes (n 礪礪 100). La méthode d’itération de Newton conduit alors à des algorithmes de division et d’extraction de racines de complexité analogue à (20).

Tests de primalité et de factorisation

Un entier m composite (non premier) possède nécessairement un facteur plus petit que 連m . Il en résulte que l’essai successif des divisions exactes de m par les nombres 2, 3, 4..., [ 連m ] constitue à la fois un algorithme de factorisation – qui détermine les diviseurs de m si m est composite – et un test de primalité – si aucun diviseur n’a été obtenu. Contrairement aux algorithmes précédemment étudiés, celui-ci est de complexité exponentielle , puisque pour un entier de n bits, le nombre d’opérations arithmétiques peut être de l’ordre de 2^{n /2}.

La base de nombreux tests de primalité est le «petit» théorème de Fermat, d’après lequel, si m est premier,

pour tout a : 1 麗 a 麗 m . Il en résulte que la découverte d’un entier a tel que a ^m-1 / 令 1 (mod m ) constitue une preuve du caractère composite de m , sans toutefois fournir de manière constructive un facteur de m . Un calcul direct montre par exemple que:

d’où il résulte que l’entier 1 234 567 est composite (en fait il est égal à 127 憐 9 721).

Le calcul d’exponentielles de type x ^e dans diverses structures algébriques s’effectue aisément par une décomposition analogue à (4):

Ainsi, x ^e s’évalue-t-il au moyen d’élévations au carré successives donnant x , x ² , x ⁴, x ⁸, ..., suivies d’au plus n produits. Il suffit de la sorte de vingt-neufs multiplications pour effectuer le test (22). De manière plus générale, un test de Fermat du type (21), (22), évalué au moyen de la formule (23), sur un nombre de n bits présente un coût qui est O(n ³) (ou O(n ² log n log log n ) si l’on utilise la multiplication rapide fondée sur la transformation de Fourier rapide).

Les tests de Fermat ne permettent cependant pas de localiser tous les nombres composites: cela tient au fait qu’il existe des entiers m – les nombres de Carmichael – tels que:

Un exemple en est le nombre 561 = 3 練11 練17.

On doit donc avoir recours à des raffinements du test de Fermat, lesquels conduisent soit à des algorithmes probabilistes de primalité (Miller-Rabin, Solovay-Strassen), soit à des algorithmes exacts. Ces méthodes permettent de déterminer pratiquement le caractère premier ou composite d’entiers comportant plusieurs milliers de chiffres décimaux.

Par contraste, le problème de la factorisation d’entiers est algorithmiquement beaucoup plus difficile. Les meilleurs algorithmes connus présentent une complexité de l’ordre de exp(c 連n logn ), ce qui représente une amélioration substantielle par rapport à l’algorithme simple en O(2n /2), mais ne permet guère de factoriser des entiers de plus de cinquante chiffres décimaux.

Codages arithmétiques à clefs publiques . La disproportion entre la complexité algorithmique de la factorisation et la complexité de la construction de nombres premiers est à l’origine d’un système de codage dû à Rivest, Shamir et Adleman (1979). Soit m = pq un nombre composite produit de deux facteurs premiers p et q ; les fonctions:

sont inverses l’une de l’autre si r et s vérifient la condition qui généralise le «petit» théorème de Fermat:

On peut ainsi utiliser C et D comme fonctions de codage et de écodage pour la transmission d’informations. Contrairement aux systèmes de codage classique, la connaissance de C (c’est-à-dire de r et m ) ne permet pas, lorsque m 礪 10¹⁰⁰, la construction de D, qui repose d’après (25) sur une factorisation de m . Cette observation permet la constitution de systèmes de codages dits à clefs publiques permettant l’échange d’informations confidentielles entre utilisateurs sur un canal public: chaque utilisateur U construit un couple de nombres premiers p , q 礪 10⁵⁰ d’où il déduit m, r et s ; il rend publique la fonction C(x ) (c’est-à-dire les entiers m et r ). Tout autre utilisateur du système peut coder des informations à destination de U, mais seul U, qui connaît la fonction de décodage D(x ), peut décoder les informations qui lui sont destinées.

3. Les problèmes algorithmiques du traitement de l’information

Méthodes de tri

Le problème du tri consiste, étant donné une suite x = (x ¹, x ², ..., x ⁿ ) d’éléments d’un ensemble totalement ordonné – par exemple N ou R –, à déterminer une permutation 靖 de 1, ..., n telle que:

soit triée, c’est-à-dire que:

(Il est clairement équivalent de déterminer la suite triée y ou la permutation triante 靖.)

L’algorithme de tri par échanges consécutifs, TEC, est conceptuellement le plus simple. Il consiste en (n 漣 1) phases successives:

La première phase (j = n ) propage ainsi le maximum de x ¹, x ², ..., x ⁿ en dernière position; la phase suivante j = (n 漣 1) amène le deuxième plus grand élément de la suite originale en position (n 漣 1)..., et à l’issue de l’algorithme, la suite x ¹, x ², ..., x ⁿ se retrouve triée. Le placement d’un maximum partiel s’effectue par propagation de ce maximum vers la droite selon le schéma:

Par exemple, avec n = 5 et la valeur initiale x = (5, 3, 9, 4, 2), la suite des valeurs de x obtenues est:

La complexité d’un algorithme de tri tel que TEC se mesure par le nombre de comparaisons effectuées et par le nombre de déplacements d’éléments de la suite (sur l’exemple, dix comparaisons et sept échanges). Dans le cas de l’algorithme TEC appliqué à une suite de longueur n , le nombre de comparaisons vaut exactement:

le nombre d’échanges varie selon le type d’ordre de la suite x donnée entre les limites 0 (soit x initialement triée) et n (n 漣 1)/(2) (soit x triée en ordre inverse). La complexité de l’algorithme TEC vérifie donc:

De nombreux algorithmes de tri élémentaires possèdent une complexité en O(n ²). Comme dans le cas des algorithmes arithmétiques, une conception récursive conduit à une réduction importante de complexité.

L’algorithme de tri-fusion est ainsi fondé sur le principe suivant: Supposons n pair, n = 2 m ; pour trier x ¹, x ², ..., x ⁿ , on trie séparément x ¹, x ², ..., x ^m et x ^{m +1}, x ^{m +2}, ..., x ⁿ . Soit u = (u ¹, u ², ..., u ^m ) et v = (v ¹, v ², ..., v ^m ) les résultats de ces deux tris. On obtient la suite y correspondant au tri de x par la fusion (ou interclassement) des suites u et v , l’algorithme de fusion étant défini récursivement par:

Une programmation classique fondée sur ces équations montre que la fusion de u et v s’effectue en O(|u | + |v |) opérations élémentaires. Le tri de n éléments est aussi ramené à deux tris de n /2 éléments suivi d’une fusion de complexité O(n ). Le coût du tri-fusion vérifie donc la récurrence:

dont la solution est:

Parmi les autres méthodes de tri récursif de complexité O(n log n ), la plus connue est le tri-partition, encore appelé «tri rapide» (Hoare, 1962). Le tri-partition de x = (x ¹, x ², ..., x ⁿ ) correspond à la suite de calculs:

(a ) séparer x en deux sous-ensembles x , x :

(b ) trier séparément x et x , avec pour résultats y et y ;

(c ) retourner le résultat global y = y 練 y .

L’algorithme de tri-fusion est à la base des méthodes de tri externe appliquées aux fichiers sur disque. L’algorithme de tri-partition, convenablement optimisé, est le plus rapide pour les tris en mémoire centrale d’ordinateur.

Structures de données

Une autre approche du problème du tri repose sur la construction de structures de données : il s’agit de la superposition à l’ensemble des données (un simple vecteur dans le cas du tri) d’une structure plus riche permettant un accès plus rapide aux informations ainsi complétées.

La structure de donnée la plus importante en informatique est certainement la structure d’arbre (graphe connexe sans cycle). Étant donné une suite x = (x ¹, x ², ..., x ⁿ ), un arbre binaire de recherche construit sur x est un arbre binaire (chaque sommet possède deux descendants distingués) dont les sommets internes sont étiquetés par les éléments de x de telle manière que la lecture des étiquettes en projection donne la suite triée correspondant à x (cf. figure).

L’intérêt de cette structure est de permettre facilement les opérations de recherche (c’est-à-dire répondre à la question: a est-il égal à l’une des composantes de x ?), insertion ou suppression d’éléments. La recherche d’un élément a dans l’arbre A s’effectue en comparant a à la racine r de A. Si a est plus petit que r , on poursuit la recherche (récursivement) dans le sous-arbre gauche; si a est plus grand que r , on la poursuit dans le sous-arbre droit. Il s’agit donc d’une généralisation de la recherche dichotomique classique.

Les arbres de recherche sont à la base de méthodes d’accès à des fichiers rangés en mémoire externe (disque) comme les arbres B dus à Bayer et McCreight (1970). Diverses autres catégories d’arbres sont utilisées en compilation (arbres de syntaxe), dans la programmation des systèmes informatiques (tris, gestion des files de priorité), ainsi que dans de nombreux algorithmes de graphes.

Méthodes de calcul d’adresses

Les structures de données précédemment décrites sont fondées sur des comparaisons entre les données. Une autre classe de méthodes, dites de calcul d’adresse ou de «hachage» , consiste à calculer pour chaque donnée d une valeur h (d ) qui détermine la position («adresse») de d dans une table. La fonction h est appelée fonction de hachage.

Un exemple de données x =x ¹, x ², ..., x ⁿ sera représenté en stockant x ¹ à l’adresse h (x ¹), x ² à l’adresse h (x ²)... Si la configuration particulière des données d’entrée de l’algorithme est telle que h (x ⁱ ) h (x ^j ) pour tout i j , on dispose ainsi d’une méthode d’accès direct : un enregistrement peut être localisé en O(1) opérations. Dans le cas contraire, lorsque deux ou plusieurs données partagent une même adresse a , on dit qu’il y a collision sur l’adresse a .

Les méthodes de calcul d’adresses diffèrent par la manière dont sont traitées les collisions: on peut par exemple ranger une donnée qui entre en collision avec une autre à la première adresse non occupée dans la table (méthodes d’«adressage ouvert»), ou la stocker dans une zone séparée. Le choix d’un algorithme de hachage adapté permet dans la plupart des cas de garantir un accès quasi direct aux données, soit en mémoire centrale soit en mémoire secondaire.

L’analyse d’algorithmes

Les algorithmes de cette section présentent, à la différence de nombreux algorithmes arithmétiques (multiplication rapide, transformation de Fourier discrète) un comportement qui dépend fortement de la configuration particulière des données d’entrées. On a vu pour le tri TEC que le nombre d’échanges nécessaire au tri de n éléments pouvait varier entre 0 et n (n 漣 1)/(2). On obtient une mesure plus significative de la complexité des algorithmes en évaluant les valeurs moyennes (espérances) des coûts sous divers modèles probabilistes naturels (indépendance des x ⁱ , uniformité de distribution des valeurs de la fonction de hachage...).

Ces évaluations de complexité moyenne nécessitent le comptage de structures finies: permutations dans le cas du tri, suites d’adresses dans les cas des algorithmes de hachage. On utilise pour cela les méthodes de l’analyse combinatoire (cf. analyse COMBINATOIRE). À titre d’exemple, on montre que la probabilité p ^{n, k} que k échanges soient nécessaires pour trier n éléments par l’algorithme TEC vérifie:

Des méthodes d’analyse asymptotique sont ensuite utilisées pour simplifier les expressions obtenues. Sur le même exemple, on démontre que la distribution du nombre d’échanges est approchée par une loi gaussienne étroitement centrée autour de la valeur moyenne n (n 漣 1)/(4) ^{[cf. PROBABILITÉS (CALCUL DES)]}.

De telles évaluations détaillées du coût des diverses opérations intervenant dans la programmation constituent l’analyse de l’algorithme. Ce sont elles qui président à la sélection de la solution algorithmique la mieux adaptée à un problème donné, ainsi qu’au choix entre différentes optimisations possibles.

4. Algorithmes combinatoires

Entrent dans la catégorie des problèmes combinatoires , en informatique, les problèmes qui consistent à déterminer, pour une donnée d , si est satisfaite une condition:

où:

(a ) S(d ) est l’espace de recherche (l’espace des solutions potentielles) de taille exponentielle en la taille de d ;

(b ) Q est une condition facilement vérifiable algorithmiquement (c’est-à-dire en un temps polynomial en la taille de ses arguments).

L’exemple le plus simple est le problème du sac à dos . Sous sa forme la plus élémentaire, il consiste, pour une donnée d = (d ¹, d ², ..., d ^m ; M) où d ⁱ , M 捻 N, à déterminer s’il existe des s ⁱ 捻0; 1 tels que:

En termes concrets: Peut-on remplir exactement un sac de capacité M avec un sous-ensemble d’objets de taille d ¹, d ², ..., d ⁿ ? L’analogie avec (1) est immédiate: S(d ) est l’ensemble0, 1ⁿ (de taille 2ⁿ ) et la condition Q(d , s ) est la condition (2) trivialement vérifiable par addition lorsque d et s sont connus.

On reconnaîtra de même comme appartenant à cette catégorie les problèmes suivants:

– Le problème du voyageur de commerce . La donnée est constituée d’un ensemble V de villes, pour chaque paire v , v 捻 V d’une distance d (v , v ) 捻 N, et d’une borne B 捻 N. Le problème consiste à déterminer s’il existe une «tournée» de V de longueur bornée par B: soit m la cardinalité de V; il s’agit de déterminer s’il existe une permutation v size=1^靖(1), v size=1^靖(2), ..., v size=1^{靖(m )} de V telle que:

– Le problème du coloriage de graphes . Étant donné un graphe G et un entier m , déterminer si G est m -coloriable, c’est-à-dire s’il existe une fonction f de l’ensemble des sommets de G dans1, 2, ..., m telle que, pour toute arêtes , s du graphe:

– La programmation en nombres entiers. La donnée est un ensemble de formes linéaires M, L¹, L²... de Z^m dans Z (à coefficients entiers) et un ensemble d’entiers B, b ¹, b ²... Il s’agit de déterminer si le système d’inégalités:

possède une solution entière 北 捻 Z^m .

Convenablement formalisée par référence à un modèle de calcul (par exemple le modèle de la machine de Turing), et à un codage standard des données, la relation (1) définit la notion de problème NP – c’est-à-dire résoluble en temps polynomial par une machine non déterministe . Les problèmes NP sont résolubles algorithmiquement en un temps 2^{p (n )} pour un certain polynôme p : il suffit pour cela d’organiser une recherche exhaustive sur l’espace de recherche S(d ).

Il a été montré, à la suite de travaux de Cook et Karp vers 1970, que plusieurs centaines de problèmes de la classe NP, d’origine très variée en théorie des graphes, ordonnancement, théorie des jeux, optimisation combinatoire..., sont algorithmiquement équivalents: on entend par là qu’ils sont inter-réductibles au moyen de réductions algorithmiquement «efficaces», c’est-à-dire calculables en temps polynomial. Malgré l’ampleur des recherches algorithmiques, aucun algorithme n’a été trouvé qui permette de résoudre l’un quelconque de ces problèmes en un temps polynomial en la taille des données d’entrées. Ce fait donne lieu à la célèbre conjecture:

dans laquelle P désigne la classe des problèmes résolubles en temps polynomial.

Étant donné le caractère hautement plausible de cette conjecture, la recherche concernant les problèmes combinatoires s’oriente soit vers la découverte de sous-problèmes algorithmiquement résolubles rapidement (par un algorithme dans P), soit vers la découverte d’heuristiques permettant de trouver des solutions approchées rapidement.

Dans le cas des quatre problèmes précédemment cités, on a en particulier obtenu les résultats suivants:

– Problème du sac à dos: Étant donné un taux d’erreur fixé 﨎 礪 0, le problème SAC( 﨎) est obtenu en remplaçant la condition (2) par la condition plus faible:

On montre que, pour chaque 﨎 fixé, il existe un algorithme polynomial permettant de résoudre SAC( 﨎). Le problème du sac à dos est donc «polynomialement approximable».

– Problème du voyageur de commerce: Lorsque les distances vérifient l’inégalité triangulaire classique:

la construction polynomiale d’un arbre de recouvrement permet de déterminer une tournée qui soit dans un rapport à la tournée optimale d’au plus 1,5. Le problème du voyageur de commerce est donc partiellement polynomialement approximable pour des distances vérifiant l’inégalité triangulaire.

– Problème du coloriage de graphes: La situation du problème du coloriage de graphes est différente de celle des deux cas précédents. On montre en effet que le problème de détermination d’un coloriage qui soit dans un rapport 見 de l’optimum est, pour 見 麗 2, de complexité comparable au problème général. Donc, moyennant la conjecture P NP, il n’existe pas d’algorithme polynomial permettant la détermination approchée du nombre chromatique d’un graphe dans un rapport inférieur à 2.

Il a été montré, en revanche, que tout graphe planaire est coloriable avec au plus quatre couleurs (cf. théorie des GRAPHES).

– Programmation en nombres entiers: On doit à Lenstra (1981) un algorithme qui, pour un nombre fixé de variables, permet de résoudre la programmation en nombres entiers en un temps polynomial (le degré du polynôme étant fonction du nombre de variables).

Le problème dans lequel on cherche aux équations (5) une solution réelle 北 捻 R^m , et non plus entière, est connu sous le nom de programmation linéaire ^{[cf. PROGRAMMATION MATHÉMATIQUE]}. Il est résolu pratiquement par la méthode du simplexe due à Dantzig, et un résultat récent de Khatchian montre qu’il s’agit en fait d’un problème polynomial.

Ces quelques exemples donnent une idée de la diversité des approches à la réduction de complexité des problèmes d’optimisation combinatoire.

5. Échelle de complexité

L’étude précédente permet de situer divers problèmes algorithmiques sur une «échelle de complexité» présentée dans le tableau 2. Les diverses mesures de coût utilisées (opérations booléennes, opérations élémentaires sur les nombres réels, comparaisonséchanges) n’étant pas strictement équivalentes, la définition d’une telle échelle se précise par l’introduction d’un modèle de la notion de calculabilité.

Il existe enfin de nombreux autres domaines de l’informatique où ont été découverts des algorithmes efficaces. Outre l’analyse numérique, on peut citer le traitement de données textuelles, la traduction des langages de programmation, le calcul formel, les problèmes «géométriques» concernant des données multidimensionnelles... La conception d’algorithmes efficaces combine habituellement l’utilisation de propriétés spécifiques au domaine du problème et des méthodes générales d’algorithmique (récursivité, structures de données, tris, calculs d’adresses...).

• 1845; de algorithme

1 ♦ Hist. math. Relatif au système de numération dit algorithme.

2 ♦ N. f. Didact. Science qui étudie l'application des algorithmes à l'informatique.

⇒ALGORITHMIQUE, adj.

[Se rapporte toujours à un inanimé] Qui concerne l'algorithme.

A.— MATH. Qui appartient aux mathématiques et à la science des nombres. Géométrie algorithmique, mécanique algorithmique (BESCH. 1845).

Rem. Attesté aussi ds Nouv. Lar. ill., Lar. 20^e.

B.— P. ext., LOG. MATH. Qui repose sur une démarche à la fois mathématique et logique. Méthode algorithmique, p. oppos. à méthode heuristique. ,,Méthode d'exploration de problèmes utilisant des algorithmes permettant d'aboutir directement à la solution.`` (GUILH. 1969) :

• 1. Adoptons pour la durée de ce livre les termes acceptés par de nombreux cybernéticiens (surtout en Angleterre) de pensée algorithmique pour désigner la pensée régulière et mécanisable, et de pensée heuristique pour nommer la pensée capable, sous l'aiguillon de l'inspiration ou du délire, de bâtir des hypothèses, de trouver des itinéraires dans le brouillard, plus généralement de résoudre les mille problèmes confus posés par la vie de tous les jours.

A. DAVID, La Cybernétique et l'humain, 1965, p. 100.

• 2. « Quand on aura rendu univoques tous les termes du lexique LDL, on pourra donner une définition de celles des propositions possibles dans ce langage, qui sont vraies, et de celles qui sont fausses (ce critère de véracité n'est pas obligatoirement algorithmique). La direction fondamentale dans laquelle va s'engager l'élaboration ultérieure du LDL, c'est la création d'une syntaxe logique, c'est-à-dire des règles de transformation qui donneront la possibilité d'utiliser le LDL pour des déductions de conséquences par la machine ».

M. COYAUD, Introduction à l'étude des langages documentaires, 1966, p. 64.

♦ Logique algorithmique. (Cf. algorithme B). ,,Système de notations et de règles de calcul, analogues à celles de l'algèbre, permettant, soit seulement de représenter les opérations de la logique classique d'une manière plus condensée et plus rigoureuse, soit de l'étendre et de définir des opérations nouvelles, p. ex. celles qui concernent les fonctions logiques, la logique des relations etc.`` (LAL. 1968, p. 36). Syn. : logistique (LAL. 1968, p. 36).

DÉR. Algorithmiquement, adv. De manière algorithmique (A. DAVID, La Cybernétique et l'humain, 1965, p. 134).

Prononc. :[].

I.— Algorithmique, 1845 (BESCH. : Algorithmique [...] Qui appartient à la science du calcul).

II.— Algorithmiquement, 1965, supra rem.

I dér. de algorithme; suff. -ique. II dér. de algorithmique; suff. -ment².

BBG. — GUILH. 1969. — LAL. 1968.

algorithmique [algɔʀitmik] adj.

ÉTYM. 1815, H. Wronski, in D. D. L.; de algorithme.

❖

1 Hist. des sc. Relatif aux algorithmes (1.). ⇒ Mathématique.