- ПРЕДСТАВЛЕНИЕ ГРУППЫ
-
- изображение элементов группы матрицами или преобразованиями линейного пространства, при к-ром сохраняется исходная групповая структура. Поскольку достаточно хорошо изучены матричные группы, при исследовании произвольной группы стараются установить соответствие между её элементами и матрицами нек-рого фиксиров. порядка, т. е. изучать группу с помощью её линейной модели. Рассмотрение П. г. позволяет обнаружить важные свойства самих групп.
В физике естеств. образом возникают П. г. симметрии. Рассмотрим, напр., преобразования трёхмерного пространства в результате вращений системы координат. Закон преобразования векторов
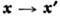 даёт, разумеется, трёхмерное П. г. вращений. Инвариантность скаляров относительно вращений позволяет ввести одномерное П. г. вращений, когда каждый элемент группы отображается на тождеств. преобразование. Можно записать закон преобразования компонент
даёт, разумеется, трёхмерное П. г. вращений. Инвариантность скаляров относительно вращений позволяет ввести одномерное П. г. вращений, когда каждый элемент группы отображается на тождеств. преобразование. Можно записать закон преобразования компонент 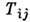 тензора ранга 2. Если рассматривать 9 величин
тензора ранга 2. Если рассматривать 9 величин 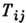 как координаты точки 9-мерного пространства, получим 9-мерное П. г. вращений. Пусть
как координаты точки 9-мерного пространства, получим 9-мерное П. г. вращений. Пусть 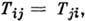 это свойство инвариантно относительно вращений; поскольку при этом остаётся лишь 6 компонент Tij, получается 6-мерное П. г. вращений, и т. д. Аналогично можно построить П. г. Лоренца. Законы преобразования спиноров дают т. н. двузначные П. г. вращений и группы Лоренца. Симметрия или антисимметрия многочастичной волновой ф-ции при перестановке тождеств. частиц даёт П. г. перестановок. Одна из целей теории П. г.- найти разл. законы преобразования физ. величин, т. е. найти всевозможные П. г. симметрии.
это свойство инвариантно относительно вращений; поскольку при этом остаётся лишь 6 компонент Tij, получается 6-мерное П. г. вращений, и т. д. Аналогично можно построить П. г. Лоренца. Законы преобразования спиноров дают т. н. двузначные П. г. вращений и группы Лоренца. Симметрия или антисимметрия многочастичной волновой ф-ции при перестановке тождеств. частиц даёт П. г. перестановок. Одна из целей теории П. г.- найти разл. законы преобразования физ. величин, т. е. найти всевозможные П. г. симметрии.П. г. тесно связаны с разл. специальными функциями матем. физики, в к-рых явно проявляются соотношения симметрии. Эта связь позволяет с единой точки зрения исследовать свойства спец. ф-ций и обнаружить новые классы ф-ций.
Развитие теории П. г. началось в кон. 19 - нач. 20 вв. в работах Г. Фробениуса (G. Frobenius) и И. Шура (I. Schur). Затем Г. Вейль (Н. Weyl), Дж. Нейман (J. Neumann) и Ю. Вигнер (Е. Wigner) продемонстрировали важность этой теории для физики.
Основные определения. П. г. G в пространстве V наз. отображение D(G, V )этой группы в набор преобразований V. Каждому элементу
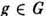 ставится в соответствие оператор T(g), действующий в пространстве V, причём
ставится в соответствие оператор T(g), действующий в пространстве V, причём 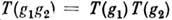 для любых
для любых 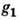 и
и 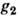 из G; Т(е) = I, где е- единичный элемент группы G,a I- единичный оператор в V. П. г. наз. линейным, если V- линейное пространство, a T(g)- линейный оператор. В дальнейшем речь будет идти только о линейных П. г. Если G - топологич. группа, то обычно требуют, чтобы T(g )непрерывно зависел от g, такие П. г. наз. непрерывными.
из G; Т(е) = I, где е- единичный элемент группы G,a I- единичный оператор в V. П. г. наз. линейным, если V- линейное пространство, a T(g)- линейный оператор. В дальнейшем речь будет идти только о линейных П. г. Если G - топологич. группа, то обычно требуют, чтобы T(g )непрерывно зависел от g, такие П. г. наз. непрерывными.Размерность пространства V обычно наз. размерностью представления, dim D(G, V), П. г. наз. вещественным (комплексным), если пространство П. г. V- вещественное (комплексное). Если D(G, V )конечномерно, то, выбрав в V базис e1, е 2,..., е п, можно задать операторы T(g )матрицами n -го порядка
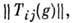 где элементы матрицы определяются соотношением
где элементы матрицы определяются соотношением 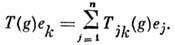 Матрица
Матрица 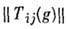 наз. матрицей представления D(G, V),a ф-цпи
наз. матрицей представления D(G, V),a ф-цпи 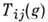 - матричными элементами представления.
- матричными элементами представления.Простейшее П. г. получается, если положить T(g)
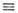 I, оно наз. единичным или тривиальным. Если группа G состоит из матриц фиксиров. порядка, то одно из П. г. получается при T(g) = g. Т. о., определение всякой линейной группы является одновременно заданием её представления в виде группы линейных операторов, т. е. группы матриц. Такие П. г. наз. определяющими. П. г. D(G, V )наз. точным, если T(g)= I, тогда и только тогда, когда g = е. В этом случае отображение g
I, оно наз. единичным или тривиальным. Если группа G состоит из матриц фиксиров. порядка, то одно из П. г. получается при T(g) = g. Т. о., определение всякой линейной группы является одновременно заданием её представления в виде группы линейных операторов, т. е. группы матриц. Такие П. г. наз. определяющими. П. г. D(G, V )наз. точным, если T(g)= I, тогда и только тогда, когда g = е. В этом случае отображение g T(g )взаимно однозначно (является изоморфизмом).
T(g )взаимно однозначно (является изоморфизмом).Если H- подгруппа группы G, то, рассматривая операторы Т (g )только при g = h
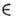 H, получим представление D(H, V), называемое сужением П. г. на подгруппу Я. Подпространство
H, получим представление D(H, V), называемое сужением П. г. на подгруппу Я. Подпространство  наз. инвариантным относительно П. г. D(G, V), если оно инвариантно относительно всех операторов T(g )этого П. г., т. е. для любых g
наз. инвариантным относительно П. г. D(G, V), если оно инвариантно относительно всех операторов T(g )этого П. г., т. е. для любых g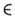 G и
G и 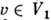 ,
, 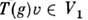 [операторы T(g )не выводят из
[операторы T(g )не выводят из 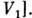
Два П. г.
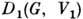 и
и 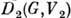 наз. эквивалентными,
наз. эквивалентными,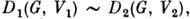 если существует линейный оператор А, взаимно однозначно отображающий
если существует линейный оператор А, взаимно однозначно отображающий 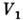 на
на 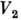 и удовлетворяющий условию
и удовлетворяющий условию 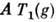 = =
= =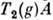 для всех g
для всех g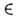 G. Если D1(G,V1) конечномерно и D1(G, V1) ~ D2(G,F2), то dimD1(G,V1)= dimD2(G, V2) и при соответствующем выборе базиса в V1 и V2 матричные элементы представлений Dl(G, V1) и D2(G, V2) совпадают.
G. Если D1(G,V1) конечномерно и D1(G, V1) ~ D2(G,F2), то dimD1(G,V1)= dimD2(G, V2) и при соответствующем выборе базиса в V1 и V2 матричные элементы представлений Dl(G, V1) и D2(G, V2) совпадают.Пусть V1
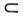 V - инвариантное подпространство относительно П. г. D(G, V). Тогда получаем П. г. D1(G,V1), к-рое наз. подпредставлением П. г. D(G, V). П. г. наз. приводимым, если оно содержит нетривиальные (т. е. отличные от тривиального и самого себя) подпредставления. П. г. D(G, V )наз. разложимым, если содержит подпредставления D1(G, V1) и D2(G, V2), такие, что V изоморфно прямой сумме своих подпространств, V = V1
V - инвариантное подпространство относительно П. г. D(G, V). Тогда получаем П. г. D1(G,V1), к-рое наз. подпредставлением П. г. D(G, V). П. г. наз. приводимым, если оно содержит нетривиальные (т. е. отличные от тривиального и самого себя) подпредставления. П. г. D(G, V )наз. разложимым, если содержит подпредставления D1(G, V1) и D2(G, V2), такие, что V изоморфно прямой сумме своих подпространств, V = V1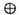 V2. В этом случае говорят, что П. г. эквивалентно прямой сумме представлений D1 и D2: D
V2. В этом случае говорят, что П. г. эквивалентно прямой сумме представлений D1 и D2: D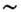 D1
D1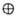 D2. Если в П. г. D для всякого подпредставления D1 существует подпредставлениеD2, такое, что D
D2. Если в П. г. D для всякого подпредставления D1 существует подпредставлениеD2, такое, что D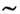 D1
D1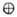 D2, то П. г. наз. вполне приводимым. В таком П. г. всякое инвариантное относительно действия операторов подпространство имеет инвариантное дополнение. Приводимое П. г. не обязательно должно быть разложимым.
D2, то П. г. наз. вполне приводимым. В таком П. г. всякое инвариантное относительно действия операторов подпространство имеет инвариантное дополнение. Приводимое П. г. не обязательно должно быть разложимым.Если в качестве базиса в пространстве F вполне приводимого конечномерного П. г. взять совокупность базисных векторов пространств подпредставлений, то матрицы, соответствующие операторам этого П. г., имеют квазидиагональный вид
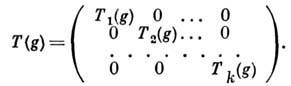
Если П. г. D(G, V )не содержит нетривиальных под-представлений, то оно наз. неприводимым. Различают алгебраич. неприводимость, т. е. отсутствие инвариантных подпространств, и топология, неприводимость, при к-рой пространство П. г. не должно содержать замкнутых инвариантных подпространств. Алгебраически неприводимое П. г. является топологически неприводимым; обратное, вообще говоря, неверно. Полноту системы неприводимых П. г. устанавливают при помощи характеров П. г.
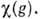 Для матричного П. г.
Для матричного П. г.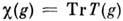
Пусть на пространствах Vl и V2 задана невырожденная билинейная форма
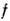 и пусть V2 - пространство П. г. D(G, V2). Всякому оператору T(g )этого П. г. можно сопоставить дуальный оператор T*(g], действующий на пространстве V1 так, что
и пусть V2 - пространство П. г. D(G, V2). Всякому оператору T(g )этого П. г. можно сопоставить дуальный оператор T*(g], действующий на пространстве V1 так, что 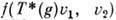 = =
= = Если вместо оператора T*(g )рассмотреть оператор T<*>(g) = T*(g-1), то множество операторов T<*> образует П. г., называемое сопряжённым к D(G, V2) относительно формы
Если вместо оператора T*(g )рассмотреть оператор T<*>(g) = T*(g-1), то множество операторов T<*> образует П. г., называемое сопряжённым к D(G, V2) относительно формы 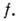 Поскольку f невырождена, размерности П. г. D(G, V2) и D<*> (G,V1 )совпадают. Для конечномерных П. г. матрицы операторов T<*>(g )имеют вид
Поскольку f невырождена, размерности П. г. D(G, V2) и D<*> (G,V1 )совпадают. Для конечномерных П. г. матрицы операторов T<*>(g )имеют вид 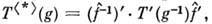 где
где 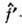 - матрица формы
- матрица формы 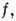 а штрих означает транспонирование. Если рассмотреть П. г. D(G,
а штрих означает транспонирование. Если рассмотреть П. г. D(G,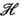 )в гильбертовом пространстве
)в гильбертовом пространстве 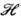 и взять в качестве формы f скалярное произведение, то множество операторов
и взять в качестве формы f скалярное произведение, то множество операторов 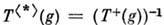 (
(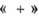 - эрмитово сопряжение) образуют П. г.
- эрмитово сопряжение) образуют П. г. 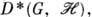 к-рое наз. сопряжённым к
к-рое наз. сопряжённым к 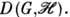 Пусть теперь все операторы П. г.
Пусть теперь все операторы П. г. 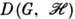 унитарны. Тогда
унитарны. Тогда 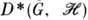 будет совпадать с
будет совпадать с 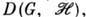 и скалярное произведение инвариантно относительно D, т. е. для любых
и скалярное произведение инвариантно относительно D, т. е. для любых 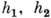 из и
из и 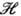 любого T(g):
любого T(g):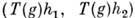 =
=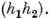 Такое П. г. наз. унитарным. Всякое П. г., сохраняющее невырожденную билинейную форму, вполне приводимо, в частности вполне приводимо всякое конечномерное унитарное П. г.
Такое П. г. наз. унитарным. Всякое П. г., сохраняющее невырожденную билинейную форму, вполне приводимо, в частности вполне приводимо всякое конечномерное унитарное П. г.П. г. D(G, V )наз. циклическим, если существует вектор
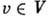 [наз. циклическим вектором для D(G, V)], такой, что замыкание линейной оболочкп всех
[наз. циклическим вектором для D(G, V)], такой, что замыкание линейной оболочкп всех 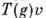 совпадает с V. Каждое унитарное П. г. является прямой суммой циклич. подпредставлений. Унитарное П. г.
совпадает с V. Каждое унитарное П. г. является прямой суммой циклич. подпредставлений. Унитарное П. г. 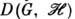 неприводимо тогда и только тогда, когда каждый ненулевой вектор
неприводимо тогда и только тогда, когда каждый ненулевой вектор 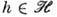 цикличен для
цикличен для 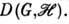
В приложениях приходится оперировать такими П. г., для к-рых процесс выделения инвариантных подпространств бесконечен. В этом случае используют обобщение понятия прямой суммы П. г.- прямой интеграл представлений.
Пусть
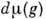 - право(лево)инвариантная мера Хаара на локально компактной группе G (см. Инвариантное интегрирование). Рассмотрим пространство
- право(лево)инвариантная мера Хаара на локально компактной группе G (см. Инвариантное интегрирование). Рассмотрим пространство 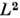 числовых (вещественных или комплексных) ф-ций
числовых (вещественных или комплексных) ф-ций 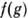 , интегрируемых с квадратом по этой мере. Обозначим
, интегрируемых с квадратом по этой мере. Обозначим 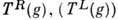 операторы преобразования в
операторы преобразования в 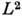 , порождённые правым (левым) сдвигом на элемент:
, порождённые правым (левым) сдвигом на элемент: 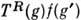 =
=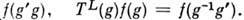 Группа операторов
Группа операторов 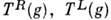 образует линейное П. г. G в пространстве
образует линейное П. г. G в пространстве 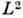 , к-рое наз. правым (левым) регулярны м П. г. Снабдив пространство
, к-рое наз. правым (левым) регулярны м П. г. Снабдив пространство  скалярным произведением
скалярным произведением 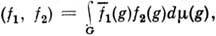 где черта означает комплексное сопряжение, можно показать, что регулярные представления унитарны.
где черта означает комплексное сопряжение, можно показать, что регулярные представления унитарны.При нахождении неприводимых представлений некомпактных (локально компактных) групп весьма эффективной оказывается теория индуцированных П. г. Индуцированное П. г. D(K, V)
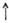 G локально компактной группы G специальным образом конструируется из представления D(K, V )замкнутой подгруппы К
G локально компактной группы G специальным образом конструируется из представления D(K, V )замкнутой подгруппы К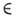 G. Пусть
G. Пусть 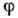 - ф-ция, отображающая G в V и удовлетворяющая условию:
- ф-ция, отображающая G в V и удовлетворяющая условию: 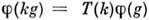 для любых g
для любых g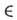 G, k
G, k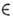 К, T(k) - оператор П. г. D(K, V). Тогда индуциров. представление U(G,
К, T(k) - оператор П. г. D(K, V). Тогда индуциров. представление U(G,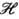 ) = D(K, V)
) = D(K, V)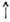 G определяется в пространстве
G определяется в пространстве 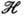 всех таких ф-ций ф-лой
всех таких ф-ций ф-лой 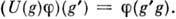 Метод индуциров. представлений является простейшим приёмом построения представлений более сложных групп из представлений более простых групп.
Метод индуциров. представлений является простейшим приёмом построения представлений более сложных групп из представлений более простых групп.В квантовой механике используют т. н. проективные П. г., когда каждому элементу g ставится в соответствие оператор T(g), действующий в пространстве V, причём для любых
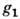 и
и 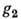 из G:
из G: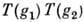 =
= 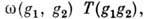 где фазовый множитель
где фазовый множитель 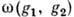 - числовая ф-ция, зависящая от
- числовая ф-ция, зависящая от 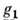 и
и 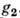 , а Т(е)- по-прежнему единичный оператор в V. На проективные П. г. непосредственно переносятся понятия эквивалентности и неприводимости П. г.
, а Т(е)- по-прежнему единичный оператор в V. На проективные П. г. непосредственно переносятся понятия эквивалентности и неприводимости П. г.Пусть
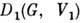 и
и 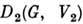 - два конечномерных П. г. G, имеющие размерности
- два конечномерных П. г. G, имеющие размерности 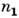 и
и 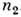 . П. г. D наз. прямым (тензорным) произведением П. г.
. П. г. D наз. прямым (тензорным) произведением П. г. 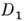 и
и 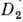 , D =
, D = , оно имеет разность п 1 п 2, а каждый его элемент представляет собой матрицу
, оно имеет разность п 1 п 2, а каждый его элемент представляет собой матрицу 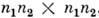 , являющуюся прямым (кронекеровым) произведением матрицы из
, являющуюся прямым (кронекеровым) произведением матрицы из 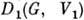 на матрицу из
на матрицу из 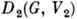 (см. Матрица). Прямое произведение .
(см. Матрица). Прямое произведение .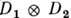 двух неприводимых конечномерных представлений
двух неприводимых конечномерных представлений 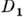 и
и 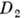 группы G неприводимо, если размерность представления
группы G неприводимо, если размерность представления 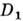 (или
(или 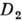 ) равна 1, в общем случае
) равна 1, в общем случае  вполне приводимо.
вполне приводимо. Напр., в квантовых системах с группой симметрии G собств. ф-ции
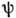 гамильтониана можно классифицировать по неприводимым П. г. G. Теория П. г. позволяет в этом случае установить т. н. правила отбора при рассмотрении процессов перехода из одного состояния в другое. Если процесс перехода задаётся оператором
гамильтониана можно классифицировать по неприводимым П. г. G. Теория П. г. позволяет в этом случае установить т. н. правила отбора при рассмотрении процессов перехода из одного состояния в другое. Если процесс перехода задаётся оператором 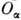 , соответствующим неприводимому П. г.
, соответствующим неприводимому П. г. 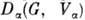 , то переход из нек-рого состояния
, то переход из нек-рого состояния 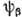 , соответствующего неприводимому П. г.
, соответствующего неприводимому П. г.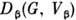 , может осуществляться лишь в те конечные состояния
, может осуществляться лишь в те конечные состояния 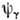 , представление к-рых
, представление к-рых 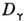 содержится в разложении прямого произведения
содержится в разложении прямого произведения 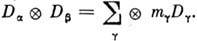
Матричные элементы оператора С, приводящего прямое произведение
 к блочнодиагональному виду [т. е.
к блочнодиагональному виду [т. е. 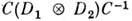 =
=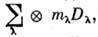 где
где 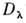 - неприводимое представление,
- неприводимое представление,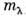 - его кратность в прямом произведении], наз. коэффициентами Клебша - Гордана. Неприводимое П. г. G, являющейся прямым произведением групп
- его кратность в прямом произведении], наз. коэффициентами Клебша - Гордана. Неприводимое П. г. G, являющейся прямым произведением групп 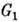 и
и 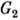 (см. Группа), есть прямое произведение их неприводимых представлений, т. е.
(см. Группа), есть прямое произведение их неприводимых представлений, т. е.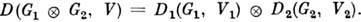
Представления некоторых групп. Коммутатив-ные группы. Любое неприводимое унитарное представление локально компактной коммутативной группы одномерно, при этом каждому элементу группы ставится в соответствие комплексное число ехр(ia). Любое представление коммутативной группы ограниченными операторами в гильбертовом пространстве является суммой (дискретной, если группа компактна) одномерных представлений.
Одним из наиб. завершённых разделов общей теории П. г. является теория представлений компактных групп, к к-рым относятся все конечные группы, группы вращений плоскости и пространства, группы SU(N )при различных N, рассматриваемые в теории элементарных частиц (см. Калибровочные поля, Унитарная симметрия), и т. д. Если группа компактна, то любому её представлению можно сопоставить эквивалентное ему унитарное представление, т. е. изучение представлений компактной группы сводится к изучению её унитарных представлений. Свойства унитарного представления полностью определяются свойствами его неприводимых компонент. Всякое неприводимое унитарное представление компактной группы конечномерно.
Если
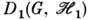 и
и 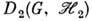 - любые два неприводимых унитарных представления компактной группы G, то матричные элементы операторов этих представлений
- любые два неприводимых унитарных представления компактной группы G, то матричные элементы операторов этих представлений 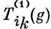 и
и 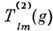 удовлетворяют соотношениям
удовлетворяют соотношениям 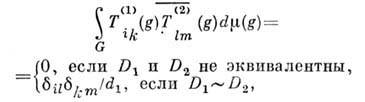
где
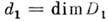 ; черта означает комплексное сопряжение. Считается, что базисы в пространствах
; черта означает комплексное сопряжение. Считается, что базисы в пространствах 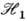 и
и 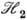 ортонормированы. Пусть
ортонормированы. Пусть 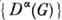 - система всех неэквивалентных неприводимых унитарных представлений компактной группы G. Ф-ции
- система всех неэквивалентных неприводимых унитарных представлений компактной группы G. Ф-ции 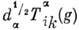 (i, k =1,...,
(i, k =1,..., 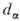 ), где
), где 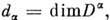 образуют полный ортонормиров. базис в пространстве
образуют полный ортонормиров. базис в пространстве 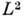 (теорема Петера - Вейля).
(теорема Петера - Вейля).Всякое неприводимое унитарное представление компактной группы эквивалентно подпредставлению её правого регулярного представления
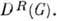
Представления конечных групп. Каждая конечная группа компактна. Поэтому утверждения, касающиеся представлений компактных групп, справедливы и для конечных групп, только во всех ф-лах необходимо заменить интегрирование по группе
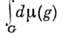 суммированием по групповым элементам
суммированием по групповым элементам 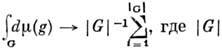 - порядок конечной группы.
- порядок конечной группы.Конечная группа имеет конечное число неприводимых П. г. Сумма квадратов размерностей всех неприводимых неэквивалентных П. г. равна порядку группы (теорема Бёрнсайда), причём все эти размерности являются делителями порядка группы. Число различных неприводимых представлений конечной группы равно числу классов сопряжённых элементов.
Представления групп Ли. Оператор T(g )представления D(G, V) n -мерной группы Ли, так же как и соответствующий элемент группы Ли, зависит от параметров
 т. е. T(g(a)) =
т. е. T(g(a)) =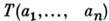 = T(a). Для т. н. дифференцируемых П. г. ф-ция Т(а )дифференцируема [так, в частности, будет, если представление D(G, V )конечномерно], можно ввести набор операторов
= T(a). Для т. н. дифференцируемых П. г. ф-ция Т(а )дифференцируема [так, в частности, будет, если представление D(G, V )конечномерно], можно ввести набор операторов 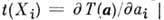 , i = 1,..., n, a=0 наз. генераторами представления D(G, V); здесь
, i = 1,..., n, a=0 наз. генераторами представления D(G, V); здесь 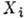 - генераторы группы. В первом приближении по
- генераторы группы. В первом приближении по 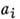 получим
получим 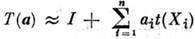 . Операторы
. Операторы 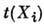 (i = 1,..., n) образуют базис Ли алгебры, к-рая наз. дифференциалом представления.
(i = 1,..., n) образуют базис Ли алгебры, к-рая наз. дифференциалом представления.Дифференциал П. г. в свою очередь является представлением алгебры Ли соответствующей группы.
Пусть g(a)- элемент однопараметрич. подгруппы группы G. Связь между П. г. D(G, V )и его дифференциалом [представлением соответствующей алгебры Ли d(A, V)]даётся ф-лой
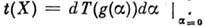 Если G- связная группа Ли, то её конечномерные представления полностью определяются своими дифференциалами. Напр., если D(G, V) - конечномерное П. г. G,a d(A, V)- представление алгебры Ли А этой группы, являющееся дифференциалом D, то всякое подпространство пространства V, инвариантное относительно D, инвариантно также относительно d. П. г. D и d неприводимы, приводимы и вполне приводимы одновременно. Если
Если G- связная группа Ли, то её конечномерные представления полностью определяются своими дифференциалами. Напр., если D(G, V) - конечномерное П. г. G,a d(A, V)- представление алгебры Ли А этой группы, являющееся дифференциалом D, то всякое подпространство пространства V, инвариантное относительно D, инвариантно также относительно d. П. г. D и d неприводимы, приводимы и вполне приводимы одновременно. Если 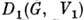 и
и 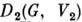 - представления связной группы Ли G, а
- представления связной группы Ли G, а 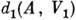 и
и 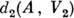 - их дифференциалы, то из эквивалентности
- их дифференциалы, то из эквивалентности 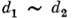 следует эквивалентность
следует эквивалентность 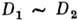 и наоборот. Конечномерные представления связных односвязных групп Ли находятся во взаимно однозначном соответствии с представлениями их алгебр Ли. Эти представления связаны ф-лой
и наоборот. Конечномерные представления связных односвязных групп Ли находятся во взаимно однозначном соответствии с представлениями их алгебр Ли. Эти представления связаны ф-лой 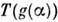 =
=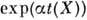 . Для унитарных представлений в гильбертовых пространствах из эквивалентности дифференциалов следует эквивалентность П. г.
. Для унитарных представлений в гильбертовых пространствах из эквивалентности дифференциалов следует эквивалентность П. г.Поэтому удобен т. н. инфинитезимальный подход, когда исследование П. г. сводят к исследованию представлений их алгебр. Каждому элементу Y из алгебры Ли А группы Ли G ставится в соответствие оператор ad (У) = [Y, X], для любого X из А. Т. к. из тождества Якоби следует, что ad ([Y, X]) =[ad(F), ad(X)], то операторы ad(Y) образуют представление алгебры А. Это представление наз. присоединённым представлением алгебры Ли. Если
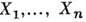 - базис алгебры А, то матричные элементы операторов ad(
- базис алгебры А, то матричные элементы операторов ad(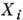 ) в этом базисе совпадают со структурными константами алгебры Ли:
) в этом базисе совпадают со структурными константами алгебры Ли: 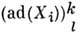 =
=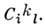
Если А- алгебра Ли связной группы G, то представление алгебры ad можно продолжить до представления группы G, действующего в А, как в векторном пространстве. Присоединённым представлением группы наз. такое отображение Ad (g, А), что exp (Ad(g)X) = gexp
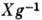 для любых X
для любых X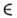 А и g
А и g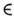 G. Размерность присоединённого П. г. совпадает с размерностью группы Ли.
G. Размерность присоединённого П. г. совпадает с размерностью группы Ли.В рамках инфинитезимального подхода развита теория конечномерных представлений полупростых групп Ли, имеющая важное значение для теории элементарных частиц. Всякое конечномерное представление полупростой алгебры вполне приводимо. Поэтому исследование конечномерных представлений полупростых алгебр сводится к исследованию неприводимых конечномерных представлений.
Для классификации неприводимых конечномерных представлений комплексных алгебр Ли используют т. н. теорию старших весов. Пусть эрмитовы операторы
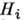 (i=1,..., r; r- размерность группы Ли G)- базисные элементы подалгебры Картана. Рассмотрим комплексное конечномерное представление d(A, V )алгебры Ли А группы G. Тогда операторы
(i=1,..., r; r- размерность группы Ли G)- базисные элементы подалгебры Картана. Рассмотрим комплексное конечномерное представление d(A, V )алгебры Ли А группы G. Тогда операторы 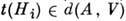 эрмитовы, они коммутируют друг с другом и поэтому имеют общие собств. векторы
эрмитовы, они коммутируют друг с другом и поэтому имеют общие собств. векторы 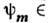 V, такие, что
V, такие, что 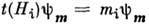 (i=1,..., r); r -мерный веществ. вектор m=
(i=1,..., r); r -мерный веществ. вектор m=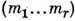 , соответствующий
, соответствующий 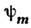 , называется весом
, называется весом 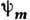 в d(A, V).
в d(A, V). Обозначим через W множество всех элементов g полупростой группы Ли G, обладающих тем свойством, что
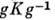 = К, где К - подгруппа Картана группы G (К- группа, алгеброй к-рой является подалгебра Картана). Множество W является подгруппой G, причём К
= К, где К - подгруппа Картана группы G (К- группа, алгеброй к-рой является подалгебра Картана). Множество W является подгруппой G, причём К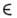 W к является нормальным делителем W. Факторгруппа W/K наз. группой отражений Вейля. Эта группа конечна.
W к является нормальным делителем W. Факторгруппа W/K наз. группой отражений Вейля. Эта группа конечна.Два веса
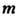 и
и 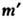 наз. эквивалентными, если они связаны друг с другом группой отражений Вейля. Число разл. весов не превышает размерности представления. Говорят, что вес
наз. эквивалентными, если они связаны друг с другом группой отражений Вейля. Число разл. весов не превышает размерности представления. Говорят, что вес  старше веса
старше веса 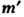 , если вектор
, если вектор 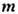 -
-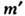 положителен, т. е. его первая отличная от нуля компонента положительна. Старший вес из множества эквивалентных весов наз. доминантным. Вес, к-рый старше всех остальных весов представления, наз. старшим весом представления.
положителен, т. е. его первая отличная от нуля компонента положительна. Старший вес из множества эквивалентных весов наз. доминантным. Вес, к-рый старше всех остальных весов представления, наз. старшим весом представления.Неприводимое конечномерное представление полупростой алгебры Ли полностью определяется своим старшим весом (теорема Картана). Для каждой простой алгебры Ли с
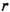 -мерной подалгеброй Картана имеется
-мерной подалгеброй Картана имеется 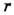 доминантных весов
доминантных весов 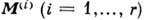 , называемых фундаментальными, таких, что остальные доминантные веса можно представить в виде
, называемых фундаментальными, таких, что остальные доминантные веса можно представить в виде 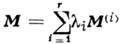 =
=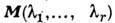 , где
, где 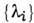 - набор неотрицат. целых чисел. Существует
- набор неотрицат. целых чисел. Существует 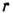 т. н. фундаментальных неприводимых конечномерных представлений простой алгебры, к-рые имеют
т. н. фундаментальных неприводимых конечномерных представлений простой алгебры, к-рые имеют 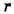 фундаментальных доминантных весов в качестве своих старших весов. Соответствующее П. г. наз. фундаментальным.
фундаментальных доминантных весов в качестве своих старших весов. Соответствующее П. г. наз. фундаментальным.До сих пор речь шла об однозначных П. г., когда каждому элементу группы g ставился в соответствие только один оператор T(g). Если группа G не является односвязной, то для того, чтобы П. г. было непрерывным, возникает необходимость каждому элементу группы g ставить одновременно в соответствие неск. разл. операторов
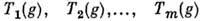 . Такое П. г. наз. m -значным.
. Такое П. г. наз. m -значным.Лит.: Випенкин Н. Я., Специальные функции и теория представлений групп, М., 1965; Желобенко Д. П., Компактные группы Ли и их представления, М., 1970; Кириллов А. А., Элементы теории представлений, 2 изд., М., 1978; Наймарк М. А., Теория представлений групп, М., 1976; Менский М. Б., Метод индуцированных представлений. Пространство - время и концепция частиц, М., 1976; Климык А. У., Матричные элементы и коэффициенты Клебша - Гордана представлений групп, К., 1979; Барут А.,
Рончка Р., Теория представлений групп и ее приложения, т. 1-2, пер. с англ., М., 1980; см. также лит. при ст. Группа.. С. И. Азаков.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.