Akademik

(от лат. operatio – действие) – одно из осн. понятий дедуктивных наук. 1) В содержат. теориях термин "О." часто употребляется как синоним термина "функция", т.е. понимается как однозначное отображение (соответствие) нек-рого множества А (элементы к-рого наз. о п е р а н д а м и, или аргументами) на нек-рое (вообще говоря, не совпадающее с А) множество В, элементы к-рого наз. результатам и применения О. (или значениями функции, или образами элементов А при отображении). По числу операндов ("аргументных мест") О. подразделяются на одноместные (унарные), двухместные (бинарные), трехместные (тернарные), вообще n-местные (n-арные для n≥1). Рассматриваются и О., определенные для бесконечных множеств в качестве операндов; пример: основная для матем. анализа О. взятия предела бесконечной последовательности (действительных или комплексных) чисел, применимая, разумеется, не к каждой, а только к фундаментальной (сходящейся) последовательности.

Результаты нек-рых О. часто обозначаются спец. терминами: "сумма" для О. сложения, "произведение" для О. умножения и т.п.; для операндов тоже часто употребляются "собственные" имена ("слагаемые", "сомножители" и т.п.); в качестве синонима "О." часто говорят "оператор" (если этот термин не используют для обозначения с и м в о л а О.); операторы, операндами к-рых служат (числовые) функции, а результатами – числа, наз. "функционалами".

2) Термин "О." часто употребляется и в расширит. смысле, когда не требуется однозначности результата; так, О. извлечения корня n-ой степени из комплексного числа сопоставляет каждому значению операнда n различных значений корня (кроме тривиального случая

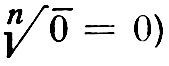Множество результатов О. для данного набора операндов при таком расширит. толковании О. может быть и бесконечным; примером может быть О. интегрирования, сопоставляющая интегрируемой функции к л а с с "первообразных", отличающихся друг от друга на произвольную аддитивную постоянную. Иногда, правда, и в таких случаях говорят об "однозначной" О., считая ее результатом весь получающийся класс (в последнем примере – "неопределенный интеграл"), а не отдельные его элементы.

3) Еще чаще понятие О. применяется в несколько суженном, по сравнению с понятием функции, смысле, когда область определения О. (множество операндов) и множество ее результатов предполагаются совпадающими – в таких случаях говорят об О., определенной на данном множестве. Область, к каждой упорядоченной n-ке элементов к-рой применима данная n-местная О., причем результат также принадлежит этой области, наз. з а м к н у т о й относительно этой n-местной О.

Большую роль в математике и логике играет вопрос о выполнимости О. (применимости ее к любому набору операндов определ. вида), что связано с необходимостью разумного расширения предметных областей. Исторически ход последоват. расширения числовых областей в математике шел начиная с натурального ряда, замкнутого относительно О. сложения и умножения; требование выполнимости О. вычитания обусловило расширение натурального ряда до множества целых чисел (положительных, отрицательных и нуля), требование выполнимости О. деления (т.е. замкнутости по отношению к этой О.) – расширение области целых чисел до области рациональных чисел – и т.д. до областей действит. и комплексных чисел.

О. и их св-ва являются осн. объектом изучения алгебры, причем, по мере развития и расширения сферы приложения формального аксиоматич. метода (см. Метод аксиоматический), все большую роль стали играть не только формализации введенных ранее "содержательных" О., но и абстрактные О. над абстрактными объектами алгебраич. теорий (групп, полей, колец и др.), определенных аксиоматически (заданием их св-в), различные интерпретации (модели) к-рых могут иметь различный смысл. В то же время в ряде случаев св-ва О. задаются не аксиоматически, а выводятся из их прямого описания в виде т.н. определяющих соотношений вида а*b = с (где а и b – операнды, * – знак О., с – результат).

Важный класс О. можно характеризовать как семантические (хотя задаются и определяются они обычно в синтаксич. терминах) – это т.н. "погружающие" О., т.е. О., переводящие формулы к.-л. формальной системы ("погружаемой") в формулы др. системы, причем в результате такого перевода ("погружения") сохраняется св-во доказуемости формул (или выводимости их из посылок). Понятие погружающей О., использованное по существу впервые А. Н. Колмогоровым при рассмотрении проблемы интерпретации интуиционистской логики в виде т.н. исчисления задач и изученное затем Н. А. Шаниным и др. учеными, служит в первую очередь при решении вопроса об относит. непротиворечивости различных дедуктивных теорий, но может рассматриваться и как способ приписывания формулам (предложениям) к.-л. теории смысла (в терминах др. теории).

В совр. математике и логике существ. роль играет связь между формальными (абстрактными) n-мерными О. в п р е д м е т н о й теории (см. Металогика, Метаязык) и с о д е р ж а т е л ь н ы м и метатеоретическими (см. Метатеория) отношениями, также n-местными; важными примерами являются соответствие между двухместной О. импликации и двухместным отношением следования и между алгебрологич. операцией эквиваленции и металогич. отношением эквивалентности (равносильности) формул логических исчислений.

Независимо от различных дефиниций понятие О. близко к понятию "действия" в широком смысле, причем "действием" можно считать как аксиоматизированное описание формальных правил перехода от операндов к результатам, так и чисто содержат. приемы "действования", "оперирования" с к.-л. объектами, в т.ч. и такие, напр., как "О. перехода от системы к ее интерпретации", "О. подстановки (имени) предмета вместо символа", "О. измерения" и т.п. Терминам "О." и "оператор" придается также часто смысл, специфичный для к.-л. более или менее широкой конкретной теории ("операторное исчисление", "операторное программирование", "операционный анализ" и др.). См. также Математика, Исчисление.