- ОБЪЁМНЫЙ РЕЗОНАТОР
-
электромагнитный, обычно замкнутая полость с хорошо проводящими стенками, внутри к-рой могут существовать свободные эл.-магн. колебания. Наиболее распространены О. р. цилиндрич., сферич. и тороидальной формы. Период собственных колебаний T=2p/w (w — круговая частота) не превышает времени прохождения волны между наиболее отдалёнными стенками; T?l/c (с — скорость распространения света в заполняющей О. р. среде, обычно в воздухе, в вакууме). Поэтому в ДВ диапазонах О. р. оказываются слишком громоздкими (I =l=сТ), и только начиная с СВЧ диапазона (l?10—20 см) их применение технически оправдано. С другой стороны, именно в этом диапазоне колебат. системы с сосредоточенными параметрами становятся низкодобротными из-за больших омич. потерь или потерь на излучение.Отыскание нормальных колебаний (колебат. мод) эл.-магн. поля внутри замкнутой полости состоит в решении Максвелла уравнений при определённых граничных условиях на стенках; в частности, на поверхности идеального проводника должна обращаться в нуль тангенциальная компонента электрич. поля Et. Бесконечное, но счётное множество собств. значений этой задачи образует спектр собств. частот О. р., а соответствующие им решения дают пространств. распределения электрич. Е и магн. Н полей (моды).Простейший О. р.— отрезок радиоволновода, закрытый двумя идеально проводящими торцевыми «крышками», перпендикулярными оси Oz. Граничные условия на торцах удовлетворяются, если между стенками укладывается целое число (q) волноводных полуволн, а также если поле Е всюду внутри О. р. направлено вдоль координаты z и не зависит от неё, т. е. при kz=(p/l)q, где kz — продольное волн. число, q=0, 1,2,...,l — длина О. р. Поскольку каждая из волноводных мод характеризуется ещё и спектром поперечных волн. чисел cnm, то полный спектр волноводного О. р. определяется соотношением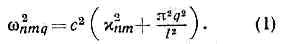 Норм. колебания волноводного О. р. классифицируются по типам соответствующих волноводных мод. Различают колебания типа TEnmq и колебания типа TMnmq. Индексы п, т, q указывают число полуволн, укладывающихся вдоль трёх измерений О. р. В случае TEnmq-колебаний вектор Е поляризован в поперечной плоскости z=const, в случае TMnmq-колебаний в этой плоскости лежит вектор Н. Иногда их обозначают Hnmq и Enmq, указывая на присутствие в полях продольных составляющих векторов Н и Е (рис. 1).
Норм. колебания волноводного О. р. классифицируются по типам соответствующих волноводных мод. Различают колебания типа TEnmq и колебания типа TMnmq. Индексы п, т, q указывают число полуволн, укладывающихся вдоль трёх измерений О. р. В случае TEnmq-колебаний вектор Е поляризован в поперечной плоскости z=const, в случае TMnmq-колебаний в этой плоскости лежит вектор Н. Иногда их обозначают Hnmq и Enmq, указывая на присутствие в полях продольных составляющих векторов Н и Е (рис. 1).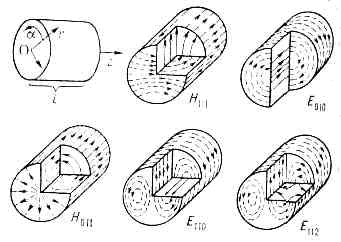 Рис. 1. Простейшие виды колебаний (моды) в цилиндрическом объёмном резонаторе. Стрелки указывают направление силовых линий электрического (сплошные линии) и магнитного (пунктир) полей.Одной и той же собств. частоте О. р. могут соответствовать две или более линейно независимых моды. Самым высоким числом вырожденных мод (12) обладают частоты wnmq (n?m?q) в сферич. или кубич. О. р. Внесение небольших неоднородностей в О. р. уменьшает число вырожденных мод, образуя систему, как бы состоящую из n связанных колебат. контуров с близкими частотами.
Рис. 1. Простейшие виды колебаний (моды) в цилиндрическом объёмном резонаторе. Стрелки указывают направление силовых линий электрического (сплошные линии) и магнитного (пунктир) полей.Одной и той же собств. частоте О. р. могут соответствовать две или более линейно независимых моды. Самым высоким числом вырожденных мод (12) обладают частоты wnmq (n?m?q) в сферич. или кубич. О. р. Внесение небольших неоднородностей в О. р. уменьшает число вырожденных мод, образуя систему, как бы состоящую из n связанных колебат. контуров с близкими частотами.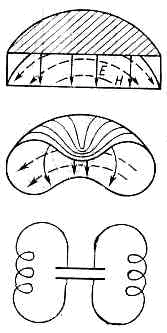 Рис. 2. Переход от цилиндрич. резонатора с модой типа E010 путём плавных деформаций стенок к резонатору, а к-ром магн. и электрич. поля пространственно разделены, почти как в колебательном контуре. Сплошные линии — силовые линии электрич. поля, пунктир — магн. поля.Чаще всего О. р. используются в режиме осн. колебания, обладающего наинизшей собств. частотой. В цилиндрич. О. р. длины l и радиуса а при l2,04а главным явл. колебание E010 (1-й индекс относится к вариации поля по углу а, 2-й — по радиусу r, 3-й — вдоль оси цилиндра oz, рис. 1), имеющее собств. частоту w010=2,04c/a. Поля в нём (Ez?0, Hаlfa?0) распределены, как в колебательном LC-контуре, в к-ром конденсатор С и самоиндукция L составляют единое целое (рис. 2). Небольшими деформациями границ О. р. можно придавать ему технологически различные, но топологически эквивалентные формы. С ростом длины при l>2,04а осн. колебанием становится H111 (Нz?0, Нr?0, Er?0, Ea?0) с частотой
Рис. 2. Переход от цилиндрич. резонатора с модой типа E010 путём плавных деформаций стенок к резонатору, а к-ром магн. и электрич. поля пространственно разделены, почти как в колебательном контуре. Сплошные линии — силовые линии электрич. поля, пунктир — магн. поля.Чаще всего О. р. используются в режиме осн. колебания, обладающего наинизшей собств. частотой. В цилиндрич. О. р. длины l и радиуса а при l2,04а главным явл. колебание E010 (1-й индекс относится к вариации поля по углу а, 2-й — по радиусу r, 3-й — вдоль оси цилиндра oz, рис. 1), имеющее собств. частоту w010=2,04c/a. Поля в нём (Ez?0, Hаlfa?0) распределены, как в колебательном LC-контуре, в к-ром конденсатор С и самоиндукция L составляют единое целое (рис. 2). Небольшими деформациями границ О. р. можно придавать ему технологически различные, но топологически эквивалентные формы. С ростом длины при l>2,04а осн. колебанием становится H111 (Нz?0, Нr?0, Er?0, Ea?0) с частотой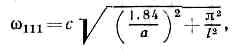 несмотря на то что оно имеет более сложную структуру, чем «конкурирующее» с ним колебание Н011 (Hz?0, Нr?0, Еa?0) с частотой
несмотря на то что оно имеет более сложную структуру, чем «конкурирующее» с ним колебание Н011 (Hz?0, Нr?0, Еa?0) с частотой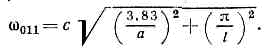 Потери энергии в среде, заполняющей полость, и поглощение в экранирующих стенках приводят к затуханию собств. колебаний. Если потери невелики, их можно учесть с помощью метода возмущений. В первом приближении все потери аддитивны. Добротность Q О. р. определяется как отношение запасённой энергии W к потерям энергии Р за период колебаний; напр., добротность Q из-за поглощения в среде равна: Q1=e'/2e" (e' и e" — действительная и мнимая части диэлектрической проницаемости), из-за поглощения в стенках Q2»V/Sd (V — объём полости, S — её поверхность, d — толщина скин-слоя, (см. СКИН-ЭФФЕКТ)). Суммарная добротность QS определяется из соотношения:1/QS=Sn1/Qn. (2)Добротности О. р. на осн. колебаниях в диапазоне СВЧ достигают 103, а при использовании сверхпроводящих экранов (см. СВЕРХПРОВОДИМОСТЬ) могут достигать 106.Возбуждение О. р., как и радиоволноводов, происходит с помощью петель, штырей, щелей, отверстий и т. п. (см. АНТЕННА). О. р. с металлич. стенками широко применяются в технике СВЧ как частотные фильтры и резонансные колебат. системы генераторов, усилителей, приёмных устройств, ускорителей, спектр-анализаторов и др. Но, начиная с частот =1011 Гц, О. р. при работе на осн. моде становятся слишком малыми (l =1 мм), и поскольку толщина скин-слоя 8 пропорц. ?l, а размеры О. р. уменьшаются пропорц. А, его добротность ухудшается по закону Q=?l. Применение же больших О. р. с возбуждением высших мод затруднено из-за очень плотного спектра собств. частот. Поэтому в миллиметровом, субмиллиметровом и оптич. диапазонах О. р. вытеснены открытыми резонаторами, в к-рых осуществляется разрежение спектра за счёт высвечивания поперечных мод с большими индексами m и n через открытые участки боковых поверхностей (см. КВАЗИОПТИКА, ОПТИЧЕСКИЙ РЕЗОНАТОР).
Потери энергии в среде, заполняющей полость, и поглощение в экранирующих стенках приводят к затуханию собств. колебаний. Если потери невелики, их можно учесть с помощью метода возмущений. В первом приближении все потери аддитивны. Добротность Q О. р. определяется как отношение запасённой энергии W к потерям энергии Р за период колебаний; напр., добротность Q из-за поглощения в среде равна: Q1=e'/2e" (e' и e" — действительная и мнимая части диэлектрической проницаемости), из-за поглощения в стенках Q2»V/Sd (V — объём полости, S — её поверхность, d — толщина скин-слоя, (см. СКИН-ЭФФЕКТ)). Суммарная добротность QS определяется из соотношения:1/QS=Sn1/Qn. (2)Добротности О. р. на осн. колебаниях в диапазоне СВЧ достигают 103, а при использовании сверхпроводящих экранов (см. СВЕРХПРОВОДИМОСТЬ) могут достигать 106.Возбуждение О. р., как и радиоволноводов, происходит с помощью петель, штырей, щелей, отверстий и т. п. (см. АНТЕННА). О. р. с металлич. стенками широко применяются в технике СВЧ как частотные фильтры и резонансные колебат. системы генераторов, усилителей, приёмных устройств, ускорителей, спектр-анализаторов и др. Но, начиная с частот =1011 Гц, О. р. при работе на осн. моде становятся слишком малыми (l =1 мм), и поскольку толщина скин-слоя 8 пропорц. ?l, а размеры О. р. уменьшаются пропорц. А, его добротность ухудшается по закону Q=?l. Применение же больших О. р. с возбуждением высших мод затруднено из-за очень плотного спектра собств. частот. Поэтому в миллиметровом, субмиллиметровом и оптич. диапазонах О. р. вытеснены открытыми резонаторами, в к-рых осуществляется разрежение спектра за счёт высвечивания поперечных мод с большими индексами m и n через открытые участки боковых поверхностей (см. КВАЗИОПТИКА, ОПТИЧЕСКИЙ РЕЗОНАТОР).
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- ОБЪЁМНЫЙ РЕЗОНАТОР
-
электромагнитный- замкнутая или почти замкнутая полость с хорошо проводящими стенками, внутри к-рой могут существовать слабозатухающие эл.-магн. колебания. О. р. могут иметь разл. формы экранирующих (проводящих) оболочек: сферические, цилиндрические, прямоугольные и т. п. Существуют О. р. с мпогосвязнымив сечениях границами, напр. бисферические, коаксиальные. Хотя под О. р. всегда подразумевают трёхмерные объекты, иногда говорят о двумерных и дажеодномерных О. р., имея в виду системы, поля в к-рых слабо зависят от однойили двух декартовых координат.
Простейшей моделью, описывающей спектральныесвойства одномерного О. р., является идеальный интерферометр Фабри -Перо, состоящий из двух бесконечно проводящих плоскостей, между к-рымн, последовательно отражаясь, "мечется" плоская эл.-магн. волна. Как и в случаеструны с жёстко закреплёнными концами, в такой системе возможны собственные(нормальные) синусоидальные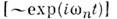 колебания (моды) с частотами
колебания (моды) с частотами 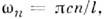 где l - расстояние между отражателями (при заполнении средой с проницаемостями
где l - расстояние между отражателями (при заполнении средой с проницаемостями 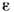 и
и 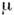 надо заменить с на
надо заменить с на 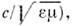 п=1,2, 3,... - число полуволн
п=1,2, 3,... - число полуволн 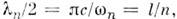 укладывающихся между пластинами.
укладывающихся между пластинами.
В двумерных и трёхмерных О. р. общая картинасобств. эл.-магн. колебаний существенно богаче по спектру собств. частот, поляризац. характеристикам и по распределению полей в пространстве. Дляотыскания собств. колебаний эл.-магн. поля в таких О. р. приходится решатькраевую задачу для Максвелла уравнений с зависящими от проводимостистенок граничными условиями. Обычно вначале рассчитывают т. и. идеальныйО. р., у к-рого потери в заполняющей среде и на излучение отсутствуют, а стенки являются бесконечно проводящими (идеально отражающими). При этомзадача о собств. колебаниях сводится (в однородной среде) к решению векторного волнового уравнения для поля Е при условии обращения в нульего тангенциальной составляющей на стенках резонатора S: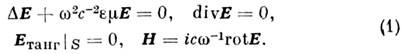
Прямоугольный резонатор. Если полостьО. р. представляет собой прямоуг. параллелепипед 0
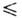 х
х 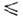 а,О
а,О 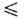 у
у 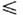 b,0
b,0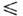 z
z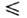 l (рис.1), то при решении задачи (1) используют декартову систему координат, вк-рой переменные векторного волнового ур-ния допускают разделение. ТакойО. р. можно рассматривать как "закороченный" (перегороженный проводящимистенками) отрезок прямоуг. волновода металлического, ориентированный, напр., в z -направлснии и имеющий длину l; он напоминает интерферометрФабри - Перо с той лишь разницей, что между плоскостями z=0 и z= l
l (рис.1), то при решении задачи (1) используют декартову систему координат, вк-рой переменные векторного волнового ур-ния допускают разделение. ТакойО. р. можно рассматривать как "закороченный" (перегороженный проводящимистенками) отрезок прямоуг. волновода металлического, ориентированный, напр., в z -направлснии и имеющий длину l; он напоминает интерферометрФабри - Перо с той лишь разницей, что между плоскостями z=0 и z= l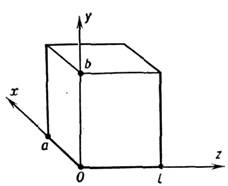
Рис. 1. Прямоугольный объёмный резонатор.
теперь "мечутся" волноводные моды, т. е. плоские неоднородные волны. Поэтому классификацию собств. колебаний прямоуг. О. р. обычно производят по типам волноводных мод, как бы "пойманных" междуплоскостями z = 0, z = l. Различают колебания ТЕ птр- и TМ птр -типов. В первом случае речь идёт о стоячей волноводной ТЕ -волне, в к-рой вектор Е поляризован в плоскости z= const, а проекции полей Еи Нна оси ( х, y,z )имеют вид
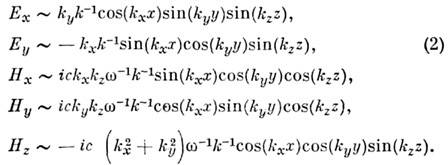
Здесь kx,k у,kz - компоненты волнового числа k:
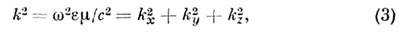
причём граничное условие
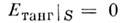 фиксирует величины этих компонент
фиксирует величины этих компонент 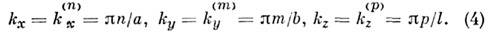
Следовательно, спектр собств. частот определяетсяф-лой
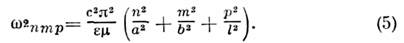
Индексы n, т, р пробегаютзначения 0, 1, 2,..., но в нуль может обращаться только один из них. Мин. собств. частота свойственна моде, у к-рой равен нулю индекс, относящийсяк наим. размеру О. р., напр. при lb а это
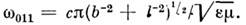 Структура поля в такой моде, а также структура поля моды TE111 воспроизведенына рис. 2. Поля типа ТМ птр можно получить из (2 )заменой E - > Н, Н - > Е,
Структура поля в такой моде, а также структура поля моды TE111 воспроизведенына рис. 2. Поля типа ТМ птр можно получить из (2 )заменой E - > Н, Н - > Е,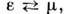 однакопри этом граничное условие
однакопри этом граничное условие 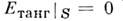 преобразуетсяв
преобразуетсяв 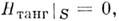 т. е. изменяются эл.-динамич. свойства стенок резонатора: они вместо "электрических"становятся "магнитными".
т. е. изменяются эл.-динамич. свойства стенок резонатора: они вместо "электрических"становятся "магнитными".
Для записи TМ -полей в идеальномО. р. с "электрическими" стенками соответствующее "магнитным" стенкам решениенеобходимо сдвинуть на четверть периода, т. е. заменить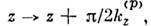
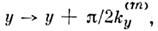
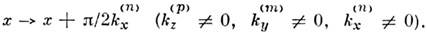 В результате такого сдвига спектр собств. колебаний (4), (5) останетсябез изменений, но ни один из индексов п, т, р не сможет уже приниматьнулевое значение, все они будут начинаться с 1: п =1, 2, 3,...; т=1, 2, 3, ...; р =1, 2, 3,.... Распределение поля в моде типа ТМ111 показано на рис. 3. Т. о., все собств. колебанияизображённого на рис. 1 идеального О. р. с ненулевыми индексами, п
В результате такого сдвига спектр собств. колебаний (4), (5) останетсябез изменений, но ни один из индексов п, т, р не сможет уже приниматьнулевое значение, все они будут начинаться с 1: п =1, 2, 3,...; т=1, 2, 3, ...; р =1, 2, 3,.... Распределение поля в моде типа ТМ111 показано на рис. 3. Т. о., все собств. колебанияизображённого на рис. 1 идеального О. р. с ненулевыми индексами, п 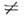 0,m
0,m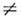 0,р
0,р 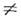 0, оказываются, ло крайней мере, двукратно вырожденными по ТЕ- и ТМ -поляризацпям. Степень вырождения может быть и более высокой, если к.-л. из размеров а,b, l совпадают между собой. Макс, кратность вырождения (12) достигаетсядля частот
0, оказываются, ло крайней мере, двукратно вырожденными по ТЕ- и ТМ -поляризацпям. Степень вырождения может быть и более высокой, если к.-л. из размеров а,b, l совпадают между собой. Макс, кратность вырождения (12) достигаетсядля частот 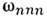 кубического О. р. ( а = b =l).
кубического О. р. ( а = b =l).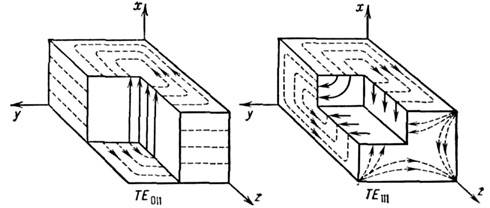
Рис. 2. Простейшие колебания (моды) TЕ -типав прямоугольном объёмном резонаторе. Распределение электрическ (сплошныелинии) и магнитного (пунктир) полей.
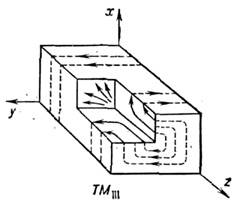
Рис. 3, Распределение электрического (сплошныелинии) и магнитного (пунктир) полей в моде типа TМ111 прямоугольного объёмного резонатора.
Резонаторы, в к-рых возбуждены вырожденныемоды, эквивалентны LC -контурам, имеющим одну и ту же собств. частоту
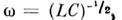 но никак не связанным друг с другом. При наличии индуктивной или ёмкостнойсвязи вырождение снимается, такая система контуров будет колебаться нановых нормальных частотах, различающихся между собой. В случае двух контуров(двух мод) зависимость новых частот от старых определяется известным графикомВина (см. также Связанные системы). ВО. р. связь между вырожденнымимодами может осуществляться небольшой деформацией стенок или внесениемвнутрь небольших возмущающих тел, напр. проводящих шариков радиусом
но никак не связанным друг с другом. При наличии индуктивной или ёмкостнойсвязи вырождение снимается, такая система контуров будет колебаться нановых нормальных частотах, различающихся между собой. В случае двух контуров(двух мод) зависимость новых частот от старых определяется известным графикомВина (см. также Связанные системы). ВО. р. связь между вырожденнымимодами может осуществляться небольшой деформацией стенок или внесениемвнутрь небольших возмущающих тел, напр. проводящих шариков радиусом 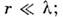 при помещении последних в пучности поля Е(Н )связь получается ёмкостной(индуктивной). На такой перестройке О. р. при внесении внутрь малых локализов. вкраплений основан один из методов измерений распределения полей в О. р.
при помещении последних в пучности поля Е(Н )связь получается ёмкостной(индуктивной). На такой перестройке О. р. при внесении внутрь малых локализов. вкраплений основан один из методов измерений распределения полей в О. р.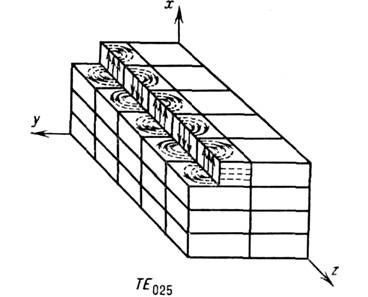
Рис. 4. Разбиение колебания ТЕ025 прямоугольного объёмного резонатора на "подмоды" типа TE011.
В прямоуг. О. р. поля имеют ячеистую структуру:любая высокая мода в них разбивается на "подмоды" типа ТМ 111,TE111, или ТЕ 011, как это показано нарис. 4. Низкие моды прямоуг. О. р. следует рассматривать в качестве элементарных. В технике довольно часто (но не всегда) О. р. используют в режиме одногоколебания, обычно обладающего наинпзшей собств. частотой.
Цилиндрический резонатор. С помощью плавныхдеформаций стенок О. р. можно проследить за топологически подобными изменениямиструктуры собств. мод.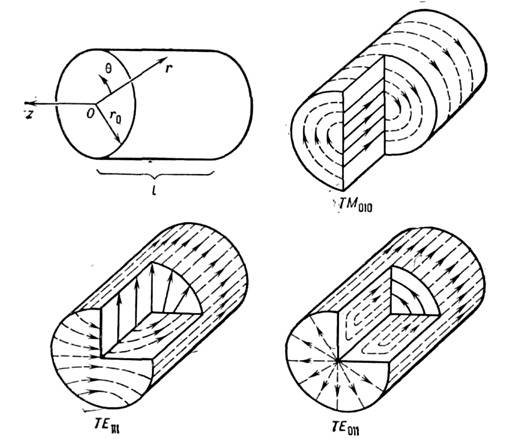
Рис. 5. Простейшие колебания (моды) в цилиндрическомобъёмном резонаторе. Распределение электрического (сплошные линии) и магнитного(пунктир) полей.
Так, осн. мода ТЕ 110 прямоуг. резонатора преобразуется в моду типа ТМ 010 цилиндрич. резонатора. Смена обозначений связана с тем, что в координатах
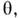 r,z (рис. 5) поле не зависит от координат
r,z (рис. 5) поле не зависит от координат 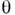 и z. Строгие количеств. данные о частотном спектре и структуре собств. колебаний цилиндрич. (и любого другого) резонатора удаётся получить толькоиз непосредств. решения краевой задачи (1): в цилиндре радиусом r0 и высотой l при l < 2,04r0 мин. частотуимеет мода TM010,
и z. Строгие количеств. данные о частотном спектре и структуре собств. колебаний цилиндрич. (и любого другого) резонатора удаётся получить толькоиз непосредств. решения краевой задачи (1): в цилиндре радиусом r0 и высотой l при l < 2,04r0 мин. частотуимеет мода TM010,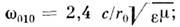 . ростом l происходит смена осн. колебания, им становится мода TE111 (Hz
. ростом l происходит смена осн. колебания, им становится мода TE111 (Hz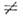 0, Н r
0, Н r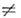 0, Е r
0, Е r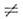 0,
0,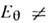 0),
0),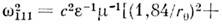
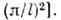 Среди собств. колебаний цилнндрич. резонатора типа ТЕ наиб. простойструктурой обладает симметричная относительно оси z мода ТЕ 011(Hz
Среди собств. колебаний цилнндрич. резонатора типа ТЕ наиб. простойструктурой обладает симметричная относительно оси z мода ТЕ 011(Hz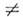 0, Н r
0, Н r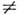 0,
0,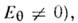
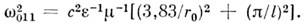
Хотя эта мода не является основной её часто используют на практике благодаря более низким, чем у моды ТЕ 111, потерям, связанным с непдеаль-ностью стенок резонатора. Фигурирующие в ф-лах длясобств. частот числа 1,84; 2,40; 3,38 являются корнями ф-ции Бесселя иеё производных: J'0(1,84) = 0, J0 (2,40)= 0, J1(3,83) = 0.
её часто используют на практике благодаря более низким, чем у моды ТЕ 111, потерям, связанным с непдеаль-ностью стенок резонатора. Фигурирующие в ф-лах длясобств. частот числа 1,84; 2,40; 3,38 являются корнями ф-ции Бесселя иеё производных: J'0(1,84) = 0, J0 (2,40)= 0, J1(3,83) = 0.
На рис. 6 показана возможность последоват. трансформации цилиндрич. резонатора в резонатор клистронного типа с гантелеобразнымаксиальным сечением, к-рый можно рассматривать как экранированный LC- контур, где конденсатор . и индуктивность L составляют единое целое.
Добротность резонатора. Реальные О. р. отличаются от идеальных О. р. прежде всего наличием потерь (в среде, заполняющейполость, в экранирующих стенках, а также в местах ввода и вывода энергии).Если потери в заполняющей среде распределены однородно, то они не вносятизменений в структуру отд. компонент полей, но превращают чисто действительныесобств. частоты в комплексные: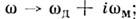 соответствующие моды становятся затухающими:
соответствующие моды становятся затухающими: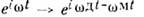 Декремент затухания
Декремент затухания 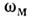 определяется путём замены в (3) и (5)
определяется путём замены в (3) и (5)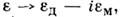
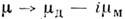 и в случае малых потерь
и в случае малых потерь 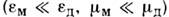 равен
равен 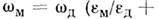
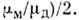 Поглощениев экранирующей оболочке, как правило, учитывают методом малых возмущений. Удобно использовать Леонтовича граничное условие для тангенциальныхсоставляющих полей Е, Н, к-рое фактически лишь слегка модифицируеткраевую задачу (1). По методу малых возмущений рассчитывают обычно и влияниеустройств ввода-вывода эл.-магн. энергии, связывающих объёмный резонаторс внешними системами.
Поглощениев экранирующей оболочке, как правило, учитывают методом малых возмущений. Удобно использовать Леонтовича граничное условие для тангенциальныхсоставляющих полей Е, Н, к-рое фактически лишь слегка модифицируеткраевую задачу (1). По методу малых возмущений рассчитывают обычно и влияниеустройств ввода-вывода эл.-магн. энергии, связывающих объёмный резонаторс внешними системами.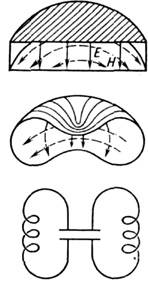
Рис. 6. Переход от цилиндрического резонаторас модой типа ТМ010 при плавной деформации стенок к резонаторуклистронного типа, в котором электрическое (сплошные линии) и магнитное(пунктир) поля пространственно разделены (как в колебательном контуре).
По аналогии с LC -контурами качествоО. р. часто характеризуют его добротностью Q. Добротность определяютлибо по ушпрению резонансных линий,
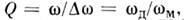 либо как отношение запасённой в О. р. энергии W (средней за периодколебаний
либо как отношение запасённой в О. р. энергии W (средней за периодколебаний 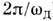 ) к мощности ср. потерь Р:Q=
) к мощности ср. потерь Р:Q=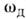 W/P. Последнееопределение всегда требует уточнения, т. к. зависит от выбора "границ раздела"между областью, где энергия запасается, и областью, где она диссипируется.
W/P. Последнееопределение всегда требует уточнения, т. к. зависит от выбора "границ раздела"между областью, где энергия запасается, и областью, где она диссипируется.
В случае высокодобротных О. р. потериможно считать аддитивными и каждому их каналу поставить в соответствиесвою (парциальную) добротность Qi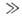 1.Так, добротность, связанная с поглощением в среде, равна
1.Так, добротность, связанная с поглощением в среде, равна 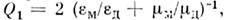 а добротность, связанная с поглощением в стенках, Q2~V/S
а добротность, связанная с поглощением в стенках, Q2~V/S (V - объём, S - поверхность полости,
(V - объём, S - поверхность полости,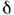 - толщина скин-слоя). Особую роль в теории О. р. играет добротность связи, или нагруженная добротность Q3, определяющая потери наизлучение вовне. В режиме оптимального резонансного возбуждения величинаQ3 равна половине суммарной добротности: Q3=Q/2 (Q-1 =
- толщина скин-слоя). Особую роль в теории О. р. играет добротность связи, или нагруженная добротность Q3, определяющая потери наизлучение вовне. В режиме оптимального резонансного возбуждения величинаQ3 равна половине суммарной добротности: Q3=Q/2 (Q-1 =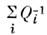 ).
).
Поскольку любой О. р. является многомодовым, то следует иметь в виду, что по мере уменьшения Qуширение резонансныхлиний может стать сравнимым с расстоянием между соседними собств. частотами, к-рые по существу уже перестают быть таковыми. При этом О. р. утрачиваетсвои избирательные (резонансные) свойства. Мин. значения добротностей, при к-рых ещё можно говорить о резонансных эффектах, ~10. Обычно добротностиО. р. характеризуются значительно более высокими числами; напр., на осн. колебаниях в СВЧ-дпапазоне они достигают 103, а при применениисверх-проводящих экранов ~106 - 107.
Как уже отмечалось, О. р. чаще всего используютна низших собств. частотах. Однако иногда необходимо работать с высокимимодами, избегая паразитного возбуждения других, "нерабочих" мод. С даннойпроблемой, к-рую наз. проблемой селекции мод, приходится сталкиваться, напр., в электронике СВЧ, где в интересах повышения мощности часто объёмрезонатора стараются делать большим по сравнению с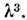
Возбуждение О. р. осуществляют обычнос помощью штырей, петель, щелей, отверстий, к к-рым подводят извне эл.-магн. энергию, примерно так же, как в случае волноводов (см. Антенна). Втеории такие возбуждающие устройства часто можно заменить на эквивалентныеим сторонние электрич. и магн. токи с плотностями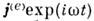 и
и 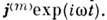 Дляэфф. возбуждения О. р. требуется, чтобы ток j(e) былориентирован вдоль поля Е, а ток j(m) - вдольполя Н нужной моды, т. к. соответствующие коэф. возбужденияпропорц. интегралам
Дляэфф. возбуждения О. р. требуется, чтобы ток j(e) былориентирован вдоль поля Е, а ток j(m) - вдольполя Н нужной моды, т. к. соответствующие коэф. возбужденияпропорц. интегралам 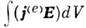 и
и 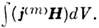 Счисто матем. позиций задача о вынужденных колебаниях О. р. сводится к решениюур-ния (1), в правой части к-рого стоит возбуждающая сила
Счисто матем. позиций задача о вынужденных колебаниях О. р. сводится к решениюур-ния (1), в правой части к-рого стоит возбуждающая сила 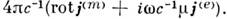
О. р. с металлич. стенками применяют втехнике СВЧ (109 - 1011 Гц) как частотные фильтрыи резонансные колебат. системы генераторов, усилителей, приёмных устройств, анализаторов спектра и др. Начиная с частот ~1011 Гц О. р. приработе на первой моде становятся излишне миниатюрными (l -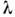 - 1 мм), к тому же их добротность ухудшается по закону Q~
- 1 мм), к тому же их добротность ухудшается по закону Q~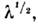 поскольку толщина скин-слоя уменьшается пропорц.
поскольку толщина скин-слоя уменьшается пропорц.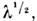 а размеры О. р. - пропорц.
а размеры О. р. - пропорц.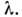 В миллиметровом, субмиллиметровом и оптич. диапазонах О. р. вытеснены большими(в масштабе
В миллиметровом, субмиллиметровом и оптич. диапазонах О. р. вытеснены большими(в масштабе 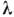 ) открытымирезонаторами квазиоптич. типа, в к-рых осуществляется разрежение спектрасобств. частот за счёт "высвечивания" части мод через открытые участкибоковых поверхностей.
) открытымирезонаторами квазиоптич. типа, в к-рых осуществляется разрежение спектрасобств. частот за счёт "высвечивания" части мод через открытые участкибоковых поверхностей.
О. р. встречаются и в природных условиях, причём экранирующие поверхности у них не обязательно хорошо проводящие. Напр., существует бисферич. О. р. Земля - ионосфера. Земля является электропроводящимэкраном, а ионосфера - рефракционным (из-за полного внутр. отражения волн).Аналогичные О. р., обычно представляющие собой отрезки волноводов диэлектрических (плоско-параллельныхили цилиндрических), встречаются и в технике.Лит.: Вайнштейн Л. А., Электромагнитныеволны, 2 изд., М., 1988; Лебедев И. В., Техника и приборы СВЧ, 2 изд.,т. 1, М., 1970; Джексон Дж., Классическая электродинамика, пер. с англ.,М., 1965; Каценеленбаум Б. 3., Высокочастотная электродинамика, М., 1966;Никольский В. В., Никольская Т. И., Электродинамика и распространение радиоволи,3 изд., М., 1989.
М. А. Миллер, А. И. Смирнов.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.