Akademik

ДОБРОТНОСТЬ

ДОБРОТНОСТЬ: величина, характеризующая резонансные свойства линейной колебат. системы; численно равна отношению резонансной частоты со к ширине резонансной кривой Dw на уровне убывания амплитуды в ?2 раза: Q=w/Dw. Принято также выражать Д. колебат. системы через отношение запасённой в ней энергии W к средней за период колебаний мощности потерь Р: Q=wW/P. Однако при наличии потерь величина запасённой энергии не может быть установлена строго и определяется путём условного разграничения диссипативных и реактивных элементов. Так, напр., в случае электрич. контуров принято запасённую энергию считать сосредоточенной в чисто реактивных элементах индуктивности L и ёмкости С, а потери связывать с протеканием тока по чисто диссипативному элементу — сопротивлению R, тогда Д.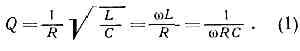

Соответственно для механич. колебат. системы с массой m, упругостью k и коэфф. трения b

Q=?(mk/b)=wm/b=k/wb. (2)

В колебат. системах с большой Д. частота и коэфф. затухания а слабозатухающих колебаний вида e-atsinwt связаны с Д. отношением

Q=w/2a=p/d->i,

где d=2pa/w — логарифмич. декремент затухания.

Д. характеризует избирательную и разрешающую способности колебат. системы: чем больше Q, тем выше резонансный отклик системы по сравнению с нерезонансным; близкие частоты w1 и w2 могут быть разрешены, если |w1-w2|->Dw=w/Q. Обычные радиоконтуры обладают Д. Q = 101 —102, для камертона Q = 102, для пьезокварцевой пластинки Q = 2•104 на частоте 20 кГц, для СВЧ резонаторов Q = 103—104, а для квазиоптич. и оптич. резонаторов =106—107.

ДОБРОТНОСТЬ: колебательной системы- величина, характеризующая резонансные свойства линейной колебат. системы; численно равна отношению резонансной частоты w к ширине резонансной кривой Dw на уровне убывания амплитуды в Ц2 раз: Q=w/Dw Принято также выражать Д. через отношение запасённой в системе энергии W к средней за период колебаний мощности потерь Р, т. е. Q=wW/P. Однако при наличии потерь величина запасённой энергии не может быть установлена строго и определяется путём условного разграничения диссипативных и реактивных элементов. Так, напр., в случае электрич. контуров запасённую энергию считают сосредоточенной в чисто реактивных элементах индуктивности L и ёмкости С, а потери связывают с протеканием тока по чисто диссииативному элементу - сопротивлению R. Тогда

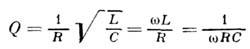
Соответственно для механич. колебат. системы с массой т, упругостью k и коэф. трения b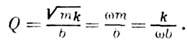

В колебат. системах с большой Д. частота и коэф. затухания a слабозатухающих колебаний вида e^-^a^tsinwt связаны с Д. отношением Q=w/2a=p/d >> 1, где d=2pa/w - декремент затухания. Д. характеризует избирательную и разрешающую способности колебат. системы: чем больше Q, тем выше резонансный отклик системы по сравнению с нерезонансным; отклики системы на одинаковые по амплитуде сигналы с близкими частотами w₁ и w₂ существенно различны по величине и, следовательно, могут быть разрешены, если |w₁-w₂|/Dw=w/Q. Обычные радиоконтуры обладают Д. Q~10-10², для камертона Q~10², для пьезокварцевой пластинки Q~2^.10⁴ на частоте 20 кГц, для СВЧ-резонаторов Q~10³-10⁴, а для квазиоптич. и оптич. резонаторов Q~10⁶-10⁷.Если в системе существует неск. источников диссипации, то для получения результирующей Д. Q_S складываются обратные величины: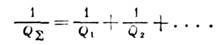

Величину Q_i,с к-рой связан отвод энергии в полезную нагрузку, наз. рабочей Д. В случае многомодовых систем с дискретным (точнее, квазидискретным) спектром собственных частот каждая из мод обладает своей Д.; в пределе, когда спектр сливается в сплошной, понятие Д. утрачивает смысл. Лит.: Cтрелков С. П., Введение в теорию колебаний, 2 изд., М., 1964; Горелик Г. С., Колебания и волны, 2 изд., М., 1959; Сивухин Д. В., Общий курс физики, 2 изд., [т. 3] - Электричество, М., 1983.М. А. Миллер.