- КОМПТОНА ЭФФЕКТ
-
(комптон-эффект), упругое рассеяние эл.-магн. излучения на свободных (или слабо связанных) эл-нах, сопровождающееся увеличением длины волны; наблюдается при рассеянии излучения малых длин волн — рентгеновского и g-излучений. Открыт в 1922 амер. физиком А. Комптоном (A. Compton) при исследовании рассеяния рентг. лучей в парафине. В К. э. впервые во всей полноте проявились корпускулярные св-ва эл.-магн. излучения (в частности, света).Согласно классич. теории рассеяния света (развитой англ. физиком Дж. Томсоном), длина световой волны при рассеянии не должна меняться: под действием периодич. электрич. поля световой волны эл-н колеблется с частотой поля и поэтому излучает вторичные (рассеянные) волны той же частоты.Первоначальная теория К. э. на основе квант. представлений была дана Комптоном и независимо от него голл. физиком П. Дебаем. По квант. теории, световая волна представляет собой поток световых квантов — фотонов. Каждый фотон имеет определённую энергию?g=hn=hc/lи импульсpg=(h/l)n,где l и n — длина волны в частота падающего света, n — единичный вектор в направлении распространения волны.К. э. в квант. теории выглядит как упругое столкновение двух ч-ц — налетающего фотона и покоящегося эл-на. В каждом акте столкновения соблюдаются законы сохранения энергии и импульса. Фотон передаёт часть своей энергии и импульса эл-ну и изменяет направление движения — рассеивается; уменьшение энергии фотона и означает увеличение длины волны рассеянного света. Эл-н, получивший от фотона энергию и импульс, приходит в движение — испытывает отдачу. Направления движения ч-ц после столкновения и их энергии определяются законами сохранения энергии и импульса. (Т. к. при рассеянии фотонов высокой энергии эл-в отдачи может приобрести значит. скорость, необходимо учитывать релятив. зависимость энергии и импульса эл-на от его скорости.) Рис. 1 иллюстрирует закон сохранения импульса при К. э. Совместное решение ур-ний, выражающих законы сохранения энергии и импульса при К. э., даёт для сдвига длины световой волны Dl ф-лу Комптона: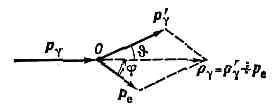 Рис. 1. Упругое столкновение фотона и эл-на в комптон-эффекте. До столкновения эл-н покоится. рg и p'g — импульсы налетающего и рассеянного фотонов; рe— импульс эл-на отдачи; q — угол рассеяния фотона; j — угол, под к-рым летит эл-н отдачи относительно направления падающего фотона.Dl=l'-l= l0(1-cosq). (1) Здесь l'— длина волны рассеянного света, q — угол рассеяния фотона, а l0=h/mec»2,426•10-10 см »0,024 ?— т. н. комптоновская длина волны эл-на (mе— масса покоя эл-на). Из ф-лы (1) следует, что Dl не зависит от длины волны падающего света, а определяется лишь углом q и максимален при q=180° (при рассеянии назад): Dlмакс= 2l0. Из этих же ур-ний можно получить выражение для энергии ?е эл-на отдачи («комптоновского» эл-на) в зависимости от угла его вылета j. Эл-ны отдачи всегда имеют составляющую скорости по направлению движения падающего фотона (т. е. j90°).0пыт подтвердил предсказанную зависимость Dl от q и наличие эл-нов отдачи. Т. о. экспериментально была доказана правильность корпускулярных представлений о механизме К. э. и тем самым — правильность исходных положений квант. теории.В реальных опытах по рассеянию фотонов в-вом эл-ны не свободны, а связаны в атомах. Если ?g велика по сравнению с энергией связи эл-нов в атоме (?св), то рассеяние происходит, как на свободных эл-нах. Если же ?g недостаточна для того, чтобы вырвать эл-н из атома, то фотон обменивается энергией и импульсом с атомом в целом. Т. к. масса атома очень велика (по сравнению с эквивалентной массой фотона ?g/c2), то отдача практически отсутствует и рассеяние фотонов происходит без изменения их энергии, т. е. без изменения длин волн,— когерентно. В тяжёлых атомах лишь периферич. эл-ны связаны слабо, поэтому в спектре рассеянного излучения присутствует как смещённая, комптоновская, линия от рассеяния на таких эл-нах, так и несмещённая линия от рассеяния на атоме в целом.
Рис. 1. Упругое столкновение фотона и эл-на в комптон-эффекте. До столкновения эл-н покоится. рg и p'g — импульсы налетающего и рассеянного фотонов; рe— импульс эл-на отдачи; q — угол рассеяния фотона; j — угол, под к-рым летит эл-н отдачи относительно направления падающего фотона.Dl=l'-l= l0(1-cosq). (1) Здесь l'— длина волны рассеянного света, q — угол рассеяния фотона, а l0=h/mec»2,426•10-10 см »0,024 ?— т. н. комптоновская длина волны эл-на (mе— масса покоя эл-на). Из ф-лы (1) следует, что Dl не зависит от длины волны падающего света, а определяется лишь углом q и максимален при q=180° (при рассеянии назад): Dlмакс= 2l0. Из этих же ур-ний можно получить выражение для энергии ?е эл-на отдачи («комптоновского» эл-на) в зависимости от угла его вылета j. Эл-ны отдачи всегда имеют составляющую скорости по направлению движения падающего фотона (т. е. j90°).0пыт подтвердил предсказанную зависимость Dl от q и наличие эл-нов отдачи. Т. о. экспериментально была доказана правильность корпускулярных представлений о механизме К. э. и тем самым — правильность исходных положений квант. теории.В реальных опытах по рассеянию фотонов в-вом эл-ны не свободны, а связаны в атомах. Если ?g велика по сравнению с энергией связи эл-нов в атоме (?св), то рассеяние происходит, как на свободных эл-нах. Если же ?g недостаточна для того, чтобы вырвать эл-н из атома, то фотон обменивается энергией и импульсом с атомом в целом. Т. к. масса атома очень велика (по сравнению с эквивалентной массой фотона ?g/c2), то отдача практически отсутствует и рассеяние фотонов происходит без изменения их энергии, т. е. без изменения длин волн,— когерентно. В тяжёлых атомах лишь периферич. эл-ны связаны слабо, поэтому в спектре рассеянного излучения присутствует как смещённая, комптоновская, линия от рассеяния на таких эл-нах, так и несмещённая линия от рассеяния на атоме в целом.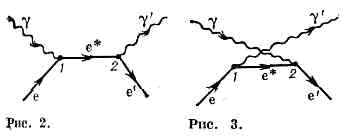 Рассмотренная упрощённая теория К. э. не позволяет вычислить все хар-ки комптоновского рассеяния, в частности интенсивность рассеяния фотонов под разными углами. Полную теорию К. э. даёт квантовая электродинамика. В этой теории К. э. представляется так: эл-н е поглощает (в точке 1) падающий на него фотон g и переходит из начального в нек-рое промежуточное (виртуальное) состояние е*, после чего виртуальный эл-н испускает (в точке 2) новый, конечный фотон g', а сам переходит в конечное состояние е'. Этот процесс можно представить в виде Фейнмана диаграммы, изображённой на рис. 2. Возможна и др. последовательность процесса: начальный эл-н сначала испускает конечный фотон и переходит в виртуальное состояние, а затем, поглощая начальный фотон, превращается в конечный эл-н (рис. 3). Испускание и поглощение эл-ном фотона происходят в результате вз-ствия эл-на с эл.-магн. полем, к-рое на диаграммах осуществляется в точках 1 и 2. Интенсивность комптоновского рассеяния зависит как от угла рассеяния, так и от длины волны падающего излучения. В угл. распределении рассеянных фотонов наблюдается асимметрия: больше фотонов рассеивается по направлению вперёд, причём эта асимметрия увеличивается с ростом ?g. Полная интенсивность (или сечение s) комптоновского рассеяния падает с ростом ?g. Зависимость s от ?g даётся ф-лой Клейна — Нишины, представляющей собой результат расчётов, отвечающих двум диаграммам Фейнмана на рис. 2 и 3. Эту ф-лу можно записать в виде:s=sT(1-f(e)),где sT=8/3pr20 — сечение томсоновского рассеяния, r0=е2/mес2»2,8•10-13 см— т. н. классич. радиус эл-на, e — энергия падающих фотонов в ед. mес2 (e=?g/mес2), а f(e) — ф-ция, возрастающая при увеличении e. При малых энергиях фотона f(e)®0 и s=sТ»7•10-24 см2. С ростом e уменьшается s и при очень высоких e оно падает до нуля, т. к. в этом случае f(e)®1 (рис. 4).
Рассмотренная упрощённая теория К. э. не позволяет вычислить все хар-ки комптоновского рассеяния, в частности интенсивность рассеяния фотонов под разными углами. Полную теорию К. э. даёт квантовая электродинамика. В этой теории К. э. представляется так: эл-н е поглощает (в точке 1) падающий на него фотон g и переходит из начального в нек-рое промежуточное (виртуальное) состояние е*, после чего виртуальный эл-н испускает (в точке 2) новый, конечный фотон g', а сам переходит в конечное состояние е'. Этот процесс можно представить в виде Фейнмана диаграммы, изображённой на рис. 2. Возможна и др. последовательность процесса: начальный эл-н сначала испускает конечный фотон и переходит в виртуальное состояние, а затем, поглощая начальный фотон, превращается в конечный эл-н (рис. 3). Испускание и поглощение эл-ном фотона происходят в результате вз-ствия эл-на с эл.-магн. полем, к-рое на диаграммах осуществляется в точках 1 и 2. Интенсивность комптоновского рассеяния зависит как от угла рассеяния, так и от длины волны падающего излучения. В угл. распределении рассеянных фотонов наблюдается асимметрия: больше фотонов рассеивается по направлению вперёд, причём эта асимметрия увеличивается с ростом ?g. Полная интенсивность (или сечение s) комптоновского рассеяния падает с ростом ?g. Зависимость s от ?g даётся ф-лой Клейна — Нишины, представляющей собой результат расчётов, отвечающих двум диаграммам Фейнмана на рис. 2 и 3. Эту ф-лу можно записать в виде:s=sT(1-f(e)),где sT=8/3pr20 — сечение томсоновского рассеяния, r0=е2/mес2»2,8•10-13 см— т. н. классич. радиус эл-на, e — энергия падающих фотонов в ед. mес2 (e=?g/mес2), а f(e) — ф-ция, возрастающая при увеличении e. При малых энергиях фотона f(e)®0 и s=sТ»7•10-24 см2. С ростом e уменьшается s и при очень высоких e оно падает до нуля, т. к. в этом случае f(e)®1 (рис. 4).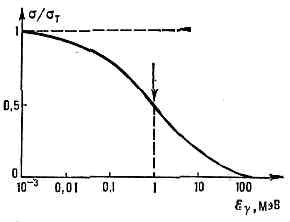 Рис. 4. График зависимости полного сечения о комптон-эффекта (в ед. сечения классич. рассеяния sT) от энергии фотона ?g ; стрелка указывает энергию, при к-рой начинается рождение электрон-позитронных пар.Такая зависимость сечения от энергии определяет место К. э. среди др. эффектов вз-ствия излучения с в-вом, ответственных за потери энергии фотонами при их пролёте через в-во. К. э. даёт гл. вклад в энергетич. потери фотонов в свинце при ?g порядка 1—10 МэВ (в более лёгком элементе — алюминии этот диапазон составляет 0,1—30 МэВ); ниже этой области с ним успешно конкурирует фотоэффект, а выше — рождение пар (см. рис. 2 в ст. (см. ГАММА-ИЗЛУЧЕНИЕ)).Комптоновское рассеяние широко используется в исследованиях g-излучения ат. ядер, лежит в основе принципа действия нек-рых гамма-спектрометров и др.К. э. возможен не только на эл-нах, но и на др. заряж. ч-цах, напр. на протонах, однако из-за большой массы протона отдача его заметна лишь при рассеянии фотонов очень высокой энергии.Обратный Комптона эффект. Если эл-ны, на к-рых упруго рассеивается эл.-магн. излучение, релятивистские, то энергия (и импульс) фотонов будет увеличиваться за счёт энергии (и импульса) эл-нов, т. е. длина волны при рассеянии будет уменьшаться. Это явление наз. обратным К. э. Его часто привлекают для объяснения механизма рентг. излучения косм. источников, образования рентг. компоненты фонового галактич. излучения, трансформации плазм. волн в эл.-магн. волны высокой частоты.
Рис. 4. График зависимости полного сечения о комптон-эффекта (в ед. сечения классич. рассеяния sT) от энергии фотона ?g ; стрелка указывает энергию, при к-рой начинается рождение электрон-позитронных пар.Такая зависимость сечения от энергии определяет место К. э. среди др. эффектов вз-ствия излучения с в-вом, ответственных за потери энергии фотонами при их пролёте через в-во. К. э. даёт гл. вклад в энергетич. потери фотонов в свинце при ?g порядка 1—10 МэВ (в более лёгком элементе — алюминии этот диапазон составляет 0,1—30 МэВ); ниже этой области с ним успешно конкурирует фотоэффект, а выше — рождение пар (см. рис. 2 в ст. (см. ГАММА-ИЗЛУЧЕНИЕ)).Комптоновское рассеяние широко используется в исследованиях g-излучения ат. ядер, лежит в основе принципа действия нек-рых гамма-спектрометров и др.К. э. возможен не только на эл-нах, но и на др. заряж. ч-цах, напр. на протонах, однако из-за большой массы протона отдача его заметна лишь при рассеянии фотонов очень высокой энергии.Обратный Комптона эффект. Если эл-ны, на к-рых упруго рассеивается эл.-магн. излучение, релятивистские, то энергия (и импульс) фотонов будет увеличиваться за счёт энергии (и импульса) эл-нов, т. е. длина волны при рассеянии будет уменьшаться. Это явление наз. обратным К. э. Его часто привлекают для объяснения механизма рентг. излучения косм. источников, образования рентг. компоненты фонового галактич. излучения, трансформации плазм. волн в эл.-магн. волны высокой частоты.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- КОМПТОНА ЭФФЕКТ
-
(комптон-эффект, комптонов-ское рассеяние) - рассеяние эл.-магн. волны на свободном электроне, сопровождающееся уменьшением частоты. Эффект наблюдается для больших частот рассеиваемого эл.-магн. излучения (в рентг. области и выше). Он проявлялся уже в первых опытах по рассеянию рснтг; лучей на свободных электронах, но впервые с требуёмой тщательностью был изучен А. Комп-тоном (A. Compton) в 1922-23. Исторически К. э. явился одним из гл. свидетельств в пользу корпускулярной природы эл.-магн. излучения (в частности, света). С точки зрения классич. электродинамики рассеяние с изменением частоты невозможно.
Элементарная теория эффекта была дана А. Комп-тоном и независимо от него П. Дебаем (P. Debye) на основе представления о том, что рентг. излучение состоит из фотонов. Для объяснения эффекта приходилось предположить, что фотон обладает как энергией
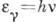 , так и импульсом
, так и импульсом 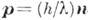 (здесь v и
(здесь v и 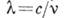 - частота и длина волны света, п - единичный вектор в направлении распространения волны).
- частота и длина волны света, п - единичный вектор в направлении распространения волны).
Комптон рассмотрел упругое рассеяние фотона на свободном покоящемся электроне (что является хорошим приближением для рассеяния фотонов рентг. лучей на атомных электронах лёгких атомов). При рассеянии фотон передаёт электрону часть энергии и импульса, что соответствует уменьшению частоты (увеличению длины волны) рассеиваемого света. Из законов сохранения энергии и импульса он получил ф-лу для сдвига длины волны:
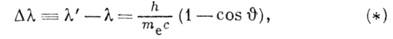
где
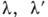 - длины волн до и после рассеяния,
- длины волн до и после рассеяния, 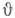 - угол рассеяния, m е - масса электрона. Параметр
- угол рассеяния, m е - масса электрона. Параметр  наз. комптоновской длиной волны электрона и равен 2,4*10-10 см. Из кинематики процесса легко также определить энергию и импульс электрона отдачи.
наз. комптоновской длиной волны электрона и равен 2,4*10-10 см. Из кинематики процесса легко также определить энергию и импульс электрона отдачи.
Поскольку ф-ла (*) основана только на кинематпч. соображениях, она оказывается справедливой и в точной теории. Из неё следует, что относит. изменение длины волны
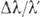 велико только для коротких длин волн, когда
велико только для коротких длин волн, когда 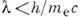
Данная Комптоном упрощённая теория эффекта не позволяет определить все характеристики компто-новского рассеяния, в частности зависимость интенсивности рассеяния от
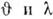 . Точная релятивистская теория К. э. была сформулирована в рамках квантовой электродинамики. (КЭД). Во втором порядке теории возмущений К. э. в КЭД описывается двумя Фейнмана диаграммами, изображёнными на рис. 1. Вычисление по этим диаграммам (с использованием Дирака уравнения для электрона) дифференц. сечения К. э. приводит к Клейна - Нишины формуле, хорошо согласующейся с опытом.
. Точная релятивистская теория К. э. была сформулирована в рамках квантовой электродинамики. (КЭД). Во втором порядке теории возмущений К. э. в КЭД описывается двумя Фейнмана диаграммами, изображёнными на рис. 1. Вычисление по этим диаграммам (с использованием Дирака уравнения для электрона) дифференц. сечения К. э. приводит к Клейна - Нишины формуле, хорошо согласующейся с опытом.
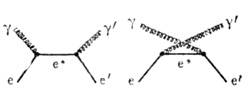
Рис. 1. Диаграммы Фсйнмана для Комптона эффекта: е,
 и
и  - электрон и фотон соответственно в начальном и конечном состояниях; е* - виртуальный электрон в промежуточном состоянии.
- электрон и фотон соответственно в начальном и конечном состояниях; е* - виртуальный электрон в промежуточном состоянии.
Для К. э. при высоких энергиях характерна острая направленность рассеянного излучения по направлению первичного фотона; с ростом энергии фотонов эта угл. асимметрия увеличивается. Полное эфф. сечение комптоновского рассеяния (полученное интегрированием по углам ф-лы Клейна - Нишины) падает с увеличением
 (рис. 2).
(рис. 2).
К. э. является одним из осн.. механизмов, определяющих потери энергии при прохождении
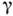 -излучения через вещество. Абс. сечение К. э., а также его соотношение с сечениями фотоэффекта и рождения пар электрон-позитрон в реальных веществах сильно зависят от ат. номера Z. На рис. 2 показано соотношение указанных процессов в свинце. В пределе нулевых частот полное сечение К. э. на отд. электроне переходит в сечение классич. (томсоновского) рассеяния
-излучения через вещество. Абс. сечение К. э., а также его соотношение с сечениями фотоэффекта и рождения пар электрон-позитрон в реальных веществах сильно зависят от ат. номера Z. На рис. 2 показано соотношение указанных процессов в свинце. В пределе нулевых частот полное сечение К. э. на отд. электроне переходит в сечение классич. (томсоновского) рассеяния 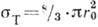 , где
, где 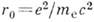 =2,8*10-13 см - т. н. классич. радиус электрона. При этом
=2,8*10-13 см - т. н. классич. радиус электрона. При этом  =6,65
=6,65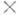 10-25 см 2. Как видно из рис. 2, при энергиях
10-25 см 2. Как видно из рис. 2, при энергиях 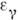 в интервале 0,5-5 МэВ К. э. даёт осн. вклад в потери энергии фотонами в свинце (в воздухе соответствующий интервал составляет 0,1-20 МэВ).
в интервале 0,5-5 МэВ К. э. даёт осн. вклад в потери энергии фотонами в свинце (в воздухе соответствующий интервал составляет 0,1-20 МэВ).
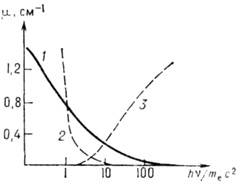
Рис. 2. Зависимость полного сечения о в свинце от энергии фотона в единицах энергии покоя электрона m еc2 для Комптона эффекта (1), фотоэффекта (2), рождения пар е + е - (3); по оси ординат отложена величина линейного поглощения фотонов
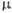 = N
= N (N - концентрация атомов вещества).
(N - концентрация атомов вещества).
Если электрон, на к-ром рассеивается фотон, не покоится, а является ультрарелятивистским с энергией
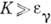 , то при столкновении электрон теряет, а фотон приобретает энергию и длина волны света при столкновении уменьшается (частота увеличивается). Такое явление наз. обратным к о м п т о н-эффектом. Если направления скоростей нач. фотонов распределены изотропно, то ср. энергия рассеянных фотонов
, то при столкновении электрон теряет, а фотон приобретает энергию и длина волны света при столкновении уменьшается (частота увеличивается). Такое явление наз. обратным к о м п т о н-эффектом. Если направления скоростей нач. фотонов распределены изотропно, то ср. энергия рассеянных фотонов 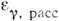 при обратном К. э. определяется соотношением
при обратном К. э. определяется соотношением
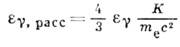
Обратный К. э. является гл. механизмом потерь энергии электронами, движущимися в магн. поле космич. радиоисточников. Он является также причиной возникновения изотропного рентг. космич. излучения с энергией
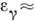 50-100 кэВ, представляющего собой фотоны отдачи при рассеянии релятивистских электронов на изотропном микроволновом космич. фоновом излучении.
50-100 кэВ, представляющего собой фотоны отдачи при рассеянии релятивистских электронов на изотропном микроволновом космич. фоновом излучении.
В процессе рассеяния электрон может поглотить один, а излучить в конечном состоянии не один (как в случае обычного К. э.), а два фотона. Это явление наз. двойным комптон-эффектом. Оно было теоретически исследовано В. Гайтлером (W. Heit-ler) и Л. Нордхеймом (L. Nordheim) в 1934. Возможен также процесс re-кратного К. э., когда в конечном состоянии излучается п фотонов. Его сечение, вообще говоря, подавлено фактором
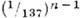 . Но в случае, когда излучаемые фотоны являются мягкими и непосредственно не регистрируются, такой процесс неотличим от обычного К. э. и имеет большое сечение. Поэтому учёт поправок от n -кратного К. э. важен для интерпретации данных по обычному К. э.
. Но в случае, когда излучаемые фотоны являются мягкими и непосредственно не регистрируются, такой процесс неотличим от обычного К. э. и имеет большое сечение. Поэтому учёт поправок от n -кратного К. э. важен для интерпретации данных по обычному К. э.
Если К. э. происходит во внеш. поле интенсивной эл.-магн. волны [где в каждом конечном интервале частоты
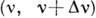 содержится много фотонов], то возможен процесс, в к-ром происходит как поглощение из внеш. поля, так и испускание электроном большого числа фотонов. Такой процесс является сложной ф-цией напряжённости внеш. электрич. поля Е и наз. нелинейным комптон-эффектом. Он происходит с заметной вероятностью при
содержится много фотонов], то возможен процесс, в к-ром происходит как поглощение из внеш. поля, так и испускание электроном большого числа фотонов. Такой процесс является сложной ф-цией напряжённости внеш. электрич. поля Е и наз. нелинейным комптон-эффектом. Он происходит с заметной вероятностью при 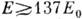 , где E0 имеет масштаб полей на электронной орбите атома водорода. Такие напряжённости электрич. поля пока недостижимы в земных условиях, но существуют на поверхности сверхплотных звёзд.
, где E0 имеет масштаб полей на электронной орбите атома водорода. Такие напряжённости электрич. поля пока недостижимы в земных условиях, но существуют на поверхности сверхплотных звёзд.
Комптоновское рассеяние происходит также на др. заряж. частицах, в частности на протоне, однако вследствие большой массы протона эффект заметен лишь при очень высоких энергиях
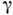 -квантов.
-квантов.
Комптоновское рассеяние используется в исследованиях
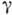 -излучения атомных ядер, а также для измерения поляризуемости элементарных частиц и ядер и лежит в основе принципа действия нек-рых гамма-спектрометров.
-излучения атомных ядер, а также для измерения поляризуемости элементарных частиц и ядер и лежит в основе принципа действия нек-рых гамма-спектрометров.
Лит.: Шпольский Э. В., Атомная физика, 7 изд., т. 1-2, М., 1984; Альфа-, бета- и гамма-спектроскопия, пер. с англ., в. 1-4, М., 1969; Л е н г К., Астрофизические формулы, пер. с англ., т. 1-2, М., 1978; Квантовая электродинамика явлений в интенсивном поле, М., 1979. М. В. Терентъев.
К. э. на связанном электроне. В рассеянии фотона связанным (атомным или молекулярным) электроном, в отличие от случая рассеяния на свободном электроне, выделяют три след. канала: рэлеевское рассеяние, при к-ром состояние мишени не меняется; комбинационное рассеяние света, в результате к-рого мишень переходит в др. связанное состояние; комптонов-ское рассеяние, сопровождающееся ионизацией.
Эффект связи электрона в атоме в нач. состоянии приводит в процессе комптоновской ионизации к уши-рению комптоновской линии, т. е. к появлению распределения по частотам
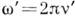 вылетающих фотонов при фиксированном угле рассеяния
вылетающих фотонов при фиксированном угле рассеяния 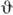 [1]. Взаимодействие электрона с ионным остатком в конечном состоянии приводит к сдвигу максимума комптоновской линии в сторону высоких частот, тем большему, чем больше энергия связи
[1]. Взаимодействие электрона с ионным остатком в конечном состоянии приводит к сдвигу максимума комптоновской линии в сторону высоких частот, тем большему, чем больше энергия связи 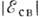 . При любых нач. энергиях фотона ширина комптоновской линии
. При любых нач. энергиях фотона ширина комптоновской линии 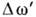 пропорц.
пропорц. 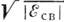 . В нерелятивистской области энергий
. В нерелятивистской области энергий 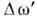 пропорц. частоте
пропорц. частоте 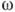 налетающего фотона,
налетающего фотона,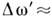
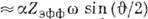 , а сдвиг её максимума порядка
, а сдвиг её максимума порядка 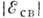 [
[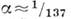 - постоянная тонкой структуры, Z эфф - эфф. заряд ядра (в единицах элементарного заряда e) для рассматриваемой электронной оболочки].
- постоянная тонкой структуры, Z эфф - эфф. заряд ядра (в единицах элементарного заряда e) для рассматриваемой электронной оболочки].
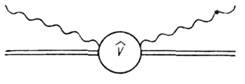
Рис. 3. Диаграмма Фейнмана типа "чайка"; двойная сплошная линия описывает электрон в поле атома, волнистая линия- фотон.
В области энергий
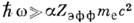 электрону в процессе комптоновской ионизации передаётся энергия, значительно большая энергии связи в атоме. Это позволяет интерпретировать рассеяние фотона как процесс, происходящий на свободном электроне, имеющем точно такое же распределение по импульсам, как в связанном состоянии. Такое рассмотрение в рамках импульсного приближения является теоретич. основой нерелятивистского метода изучения электронной структуры атомов, молекул и кристаллов - метода комптоновских, профилей [2].
электрону в процессе комптоновской ионизации передаётся энергия, значительно большая энергии связи в атоме. Это позволяет интерпретировать рассеяние фотона как процесс, происходящий на свободном электроне, имеющем точно такое же распределение по импульсам, как в связанном состоянии. Такое рассмотрение в рамках импульсного приближения является теоретич. основой нерелятивистского метода изучения электронной структуры атомов, молекул и кристаллов - метода комптоновских, профилей [2].
В области энергий
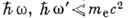 амплитуда комптон-эффекта на слабо связанном (
амплитуда комптон-эффекта на слабо связанном (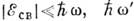 ) электроне описывается диаграммой Фейнмана типа "чайка" (рис. 3), в к-рой оператор взаимодействия
) электроне описывается диаграммой Фейнмана типа "чайка" (рис. 3), в к-рой оператор взаимодействия 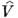 выражается через волновые векторы k,
выражается через волновые векторы k,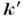 и поляризации е,
и поляризации е,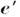 падающего и рассеянного фотонов и оператор импульса
падающего и рассеянного фотонов и оператор импульса 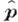 :
:
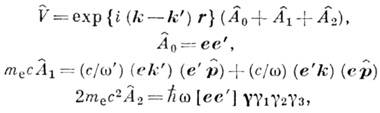
 (i = 1, 2, 3) - Дирака матрицы,_
(i = 1, 2, 3) - Дирака матрицы,_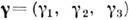 В области энергий
В области энергий 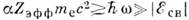 на сечение К. э. определяющее влияние оказывает взаимодействие электрона с ионным остатком в конечном состоянии, т. к. из-за приближённого выполнения закона сохранения импульса (узости комптоновской линии и малости её сдвига) вылетающий электрон обладает в среднем относительно малой энергией. При таких энергиях фотонов процесс комптоновской ионизации интерпретируется как "встряска" типа рассеяния (см. Внезапных возмущений метод). В соответствии с концепцией "встряски" [3, 4] гл. характеристикой угл. распределения рассеянных фотонов в К. э. на связанном электроне
на сечение К. э. определяющее влияние оказывает взаимодействие электрона с ионным остатком в конечном состоянии, т. к. из-за приближённого выполнения закона сохранения импульса (узости комптоновской линии и малости её сдвига) вылетающий электрон обладает в среднем относительно малой энергией. При таких энергиях фотонов процесс комптоновской ионизации интерпретируется как "встряска" типа рассеяния (см. Внезапных возмущений метод). В соответствии с концепцией "встряски" [3, 4] гл. характеристикой угл. распределения рассеянных фотонов в К. э. на связанном электроне 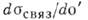 является подходящим образом выбранный "встрясочный" параметр [2]:
является подходящим образом выбранный "встрясочный" параметр [2]:

где b = 1+
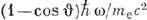 . Величиной параметра N определяются отношения эфф. сечений
. Величиной параметра N определяются отношения эфф. сечений 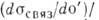
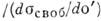 , показанных для К -электронов на рис. 4.
, показанных для К -электронов на рис. 4.
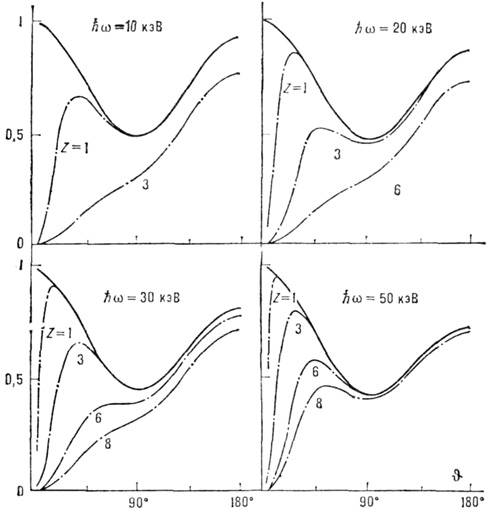
Рис. 4. Угловые распределения рассеянных фотонов
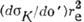 в процессе комптоновской ионизации К-оболочек лёгких элементов (штрих-пунктирные линии; re= е 2/mс 2 - классический радиус электрона); сплошные линии - расчёт по формуле Клейна - Нишины.
в процессе комптоновской ионизации К-оболочек лёгких элементов (штрих-пунктирные линии; re= е 2/mс 2 - классический радиус электрона); сплошные линии - расчёт по формуле Клейна - Нишины.
Эти отношения как ф-ции параметра N оказываются универсальными не только для К -электронов, но и для каждой конкретной атомной оболочки.
В связи с прогрессом лазерной техники в ряде исследований ставятся вопросы о влиянии сильных эл.-магн. полей на разл. элементарные атомные процессы. Имеется целый класс эффектов вынужденного поглощения или испускания фотонов внеш. лазерного поля, происходящих на фоне осн. процесса, к-рым может быть фотоионизация, комптоновская ионизация, тор-можение электрона на атоме и т. д. [4]. В области параметров, где сечения этих вынужденных процессов велики, они могут быть интерпретированы как процессы "встряски". В случаях, когда параметр N не содержит постоянной Планка (напр., в процессах испускания и рассеяния фотонов классич. электроном), вынужденные эффекты имеют классич. объяснение при любом чпсле испускаемых (поглощаемых) лазерных фотонов. Так, процесс комптоновского рассеяния жёсткого фотона с энергией
 на электроне, помещённом в интенсивное низкочастотное (с частотой
на электроне, помещённом в интенсивное низкочастотное (с частотой 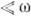 ) лазерное поле, с классич. точки зрения описывается как высокочастотное излучение электрона, находящегося в поле двух эл.-магн. волн [4].
) лазерное поле, с классич. точки зрения описывается как высокочастотное излучение электрона, находящегося в поле двух эл.-магн. волн [4].
Лит.: 1) Зоммерфельд А., Строение атома и спектры, пер. с нем., т. 2, М., 1956; 2) Б у ш у е в В. А., Кузьмин Р. Н., Неупругое рассеяние рентгеновского и синхро-тронного излучений в кристаллах, когерентные эффекты в неупругом рассеянии, "УФН", 1977, т. 122, с. 81; 3) Дыхне A.M., Юдин Г. Л., "Встряхивание" квантовой системы и характер стимулированных им переходов, "УФН", 1978, т. 125, с. 377; 4) Дыхне А. М., Юдин Г. Л., Вынужденные эффекты при "встряске" электрона во внешнем электромагнитном поле, "УФН", 1977, т. 121, с. 157. Г. Л. Юдин.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.