Akademik

GÉOMAGNÉTISME

Le géomagnétisme, ou, comme on a dit longtemps, le magnétisme terrestre, établit un lien étroit entre deux disciplines qui seraient, sans cela, pratiquement indépendantes: la géophysique interne, à laquelle on tend à réserver le nom de physique du globe, et la géophysique externe.

Le géomagnétisme est une science très étendue faisant appel à des techniques physiques variées dont plusieurs, très élaborées, lui sont propres. Il a trait à des phénomènes extrêmement différents: par leur échelle de temps, qui va de plusieurs millions d’années à une fraction de seconde, par les milieux dans lesquels on les observe, et par leurs causes qu’il faut chercher depuis l’intérieur du noyau terrestre jusqu’au Soleil. Il est en relation étroite avec d’autres branches de la géophysique (aurores polaires, ionosphère, exosphère et, plus généralement, toute la physique de la haute et très haute atmosphère), de la géologie, de la minéralogie, de l’océanographie et même de l’archéologie. Il conduit à des applications importantes, en particulier pour la navigation et la prospection géophysique ; de ce fait, on ne peut plus être un chercheur en géomagnétisme, mais seulement dans l’une de ses spécialités.

1. Mesures magnétiques

Si la science du magnétisme dérive de l’observation des propriétés de la pierre d’aimant, le géomagnétisme est né avec la boussole, qui révèle l’existence, partout sur le globe, d’un champ magnétique naturel, analogue aux champs magnétiques que l’on sait produire au laboratoire. Une bonne boussole donne l’orientation du champ dans le plan horizontal: l’axe de l’aiguille, suivi dans le sens de la pointe sud vers la pointe nord, matérialise la direction dite du nord magnétique, qui fait avec celle du nord géographique un angle D, la déclinaison magnétique ; le plan vertical défini par l’axe de l’aiguille est dit méridien magnétique. Mais le champ terrestre n’est pas horizontal; sa direction est inclinée d’un angle I, l’ inclinaison magnétique ; si l’aiguille de la boussole est horizontale, c’est parce que le constructeur l’a surchargée convenablement, du côté de la pointe sud en France. Le vecteur champ terrestre づ a pour module F, qui est son intensité ; ses projections, べ sur la verticale et で sur le plan horizontal, sont dites composantes verticale et horizontale respectivement.

Les géomagnéticiens expriment les angles D et I en degré, minute et dixième de minute; ils sont comptés positivement: D vers l’est et I vers le bas. Les autres éléments sont des intensités de champ que l’on exprime en employant généralement un sous-multiple de l’œrsted, le gamma, qui est le cent-millième d’œrsted. On peut passer dans le système légal S.I. par la relation:

On voit facilement que la connaissance de trois éléments bien choisis suffit à définir le champ づ, par exemple DIH, DHZ, DIF. Dans la région parisienne, les valeurs approchées des éléments magnétiques sont: D = 漣 5⁰ 30 (ou 5⁰ 30 W, avec W pour ouest); I = + 64⁰ 30 ; F = 0,47 Oe, d’où Z = + 0,42 Oe et H = 0,20 Oe. Il s’agit d’un ordre de grandeur, car, et c’est un fait capital en géomagnétisme, en un lieu donné, les éléments du champ subissent des variations incessantes, mais d’amplitude très faible, et, à un même instant, ces éléments sont différents d’un lieu à un autre.

La connaissance précise du champ magnétique terrestre est obtenue: d’une part, en suivant continuellement et très finement ses variations dans le temps, en quelques lieux bien choisis, les «observatoires magnétiques», répartis à la surface du globe où le champ terrestre naturel n’est pas perturbé par des champs artificiels résultant de l’activité humaine (les déplacements de masses métalliques de toutes sortes, les courants électriques, notamment ceux des chemins de fer électrifiés en courant continu, qui sont particulièrement gênants); d’autre part, en mesurant le champ en de très nombreux points sur toute la surface de la Terre, c’est-à-dire par l’exécution de «réseaux magnétiques». Ces deux activités ont entraîné la création d’un nombre considérable d’appareils assurant soit la mesure des éléments, soit l’enregistrement de leurs variations.

Mesure des éléments magnétiques

La déclinaison magnétique a été appréciée sur des boussoles rudimentaires dès le début du XVI^e siècle; on la mesure maintenant au moyen de «théodolites magnétiques» dont les plus perfectionnés assurent la précision du dixième de minute sexagésimale. L’inclinaison, observée vers la fin du XVI^e siècle, a été pendant longtemps mesurée avec des «boussoles d’inclinaison», appareils entièrement périmés dont la précision est toujours restée loin de celle de la minute; mais, avec des «inductomètres» ou «inclinomètres à bobine tournante», on approche du dixième de minute. Les mesures d’intensité n’ont vraiment commencé qu’en 1830 avec Gauss, créateur de la technique de mesure absolue de la composante H par oscillation et déviation, décrite dans tous les traités de physique. La mesure, exécutée aussi sur un théodolite magnétique, pouvait atteindre la précision de quelques gammas dans certains observatoires; cependant, la technique courante des mesures sur le terrain n’assurait même pas la précision de la dizaine de gammas. Cette méthode de Gauss est aussi complètement périmée.

Beaucoup de dispositifs ingénieux assurant des mesures assez précises dans les observatoires et rapides sur le terrain ont été créés, mais, malgré leur variété, tous ces appareils ne pouvaient être utilisés qu’à la surface du sol (et, dans d’assez mauvaises conditions, sur des navires spécialisés), car ils devaient être placés sur un support rigide et soigneusement nivelé. Une étape importante a été franchie grâce à un dispositif qui avait été adapté, pendant la Seconde Guerre mondiale, à la détection des sous-marins, la «sonde à saturation» ou fluxgate , avec laquelle l’électronique s’est imposée en géomagnétisme. Une telle sonde demande des accessoires (alimentation en courant alternatif, dispositif électronique pour mesurer la force électromotrice induite), mais peut être amenée à des dimensions centimétriques et même millimétriques. Elle permet toutes sortes de mesures et tout particulièrement celle de l’intensité totale F du champ. Placée suivant l’axe d’une bobine solénoïde, elle-même orientée parallèlement au champ à mesurer, elle vérifie la compensation exacte de F par celui de la bobine étalon. On montre facilement que, dans ce cas particulier de la mesure de F, une certaine latitude est laissée dans l’alignement des axes de la sonde et de la bobine, entre eux et avec la direction du champ. L’addition de deux autres sondes formant un trièdre trirectangle avec la sonde principale permet, par l’intermédiaire de servomoteurs, de maintenir automatiquement l’axe de la sonde suivant づ. Un tel dispositif peut être installé sur un avion (ou dans une cellule remorquée); l’enregistrement de l’intensité du courant, lui-même assujetti automatiquement à réaliser la compensation de l’intensité F, fournit une mesure continue de cette intensité. Le magnétomètre aérien , sous des formes variées, a été considérablement utilisé en prospection magnétique; il a équipé aussi des véhicules spatiaux. Pour le géomagnéticien non prospecteur, il ne fournit que l’intensité du champ; des dispositifs plus compliqués, occupant tout un gros avion, ont été mis au point aux États-Unis et au Canada: il s’agit de magnétomètres vecteurs , dans lesquels l’orientation de l’axe de la sonde (autoorienté sur づ), est constamment enregistrée, ce qui fournit la direction du champ.

De nouveaux progrès ont été réalisés avec l’apparition des magnétomètres atomiques et nucléaires . Constitués encore par une sonde, reliée à distance à tout un ensemble électronique à lecture ou à enregistrement analogique ou digital, ils fournissent des mesures très rapides (ou continues) et absolues de l’intensité F, mesures qui sont ramenées à celles, très précises, de fréquences. Leur fonctionnement étant basé sur des considérations de niveaux d’énergie, il n’y a pratiquement pas à orienter les sondes. Ces appareils ont transformé les techniques des mesures géomagnétiques, que ce soit dans les observatoires, sur le terrain – en prospection au sol ou aérienne – ou dans l’espace. Les magnétomètres à protons utilisent la résonance magnétique nucléaire (la fréquence de résonance des protons est proportionnelle au champ appliqué). Les magnétomètres à pompage optique utilisent la résonance paramagnétique électronique, la fréquence de résonance des électrons des atomes alcalins (césium ou rubidium) placés dans un champ magnétique et orientés préalablement par pompage optique. Pour la mesure des champs magnétiques très faibles et variables, on utilise un magnétomètre très sensible, le Squid (Superconducting Quantum Interference Device), constitué d’un supraconducteur et d’une fonction Josephson.

Enregistrement des variations du champ

Dans les observatoires magnétiques, on suit continuellement les variations du champ magnétique terrestre en enregistrant celles de trois au moins de ses éléments, D, H, Z en général. On dispose pour cela de variomètres , appareils construits pour répondre aux changements d’un seul élément. Par exemple, un aimant horizontal, suspendu par une fibre à constante de torsion négligeable, s’aligne continuellement dans le méridien magnétique; ses rotations sont donc égales aux changements de la déclinaison; on peut dire que c’est un D-mètre. Avec des aimants encore, et très simplement, on peut réaliser un H-mètre et un Z-mètre. En général, les courbes fournies par les trois variomètres sont enregistrées sur la même feuille, qu’on relève chaque jour: c’est un magnétogramme . Il comporte des marques de temps régulières et, grâce à des étalonnages préalables, on peut obtenir la valeur de l’élément voulu en un point quelconque du graphique, c’est-à-dire à un instant quelconque (fig. 1). Les magnétogrammes de chaque jour sont «dépouillés»: on en tire toutes sortes d’informations numériques dont il sera question plus loin, en particulier les valeurs moyennes de chaque élément pendant chaque heure (valeurs horaires), des indices d’activité magnétique, des données sur des événements divers. Ce travail de dépouillement, avec les nombreux calculs qu’il implique, est fastidieux. Il a été allégé par l’adoption de techniques de dépouillement automatique, l’enregistrement des données se faisant sur bande magnétique et le traitement étant confié à un ordinateur. On a remplacé les variomètres optiques par des sondes délivrant des intensités de courant ou, comme le magnétomètre à protons, des fréquences, informations qui peuvent être stockées sur bande magnétique.

Ce travail, dit de «magnétisme lent» parce qu’il porte sur des enregistrements à faible vitesse de déroulement, conduit à de nombreuses études qui constituent l’essentiel de ce qui va suivre. Mais on s’est aperçu que le champ magnétique terrestre présentait des variations très rapides, invisibles sur les magnétogrammes lents. Comme elles sont souvent plus ou moins périodiques, on les dit «pulsations». Leur observation est ancienne, mais leur étude, le «magnétisme rapide», n’a pris un grand développement qu’à partir de l’Année géophysique internationale 1957-1958. Ces variations sont généralement d’amplitude faible ou extrêmement faible (jusqu’au millième de gamma); il faut donc, pour les suivre, utiliser des variomètres à très grande sensibilité et des déroulements extrêmement rapides des appareils, qui sont soit des «suiveurs de spot» enregistrant sur du papier ordinaire, soit des enregistreurs sur ruban magnétique.

En ce qui concerne les variomètres, on utilise, sous des formes très variées, des sondes à induction constituées par un long noyau cylindrique en métal à forte perméabilité magnétique, entouré d’une bobine comprenant un très grand nombre de spires (des dizaines de milliers); la composante du champ parallèle à l’axe du noyau crée dans la bobine un flux d’induction dont les variations produisent une force électromotrice qui est appliquée soit à un galvanomètre, soit à un fluxmètre. De tels dispositifs n’ont une sensibilité raisonnable que dans une bande de fréquences donnée.

Champ tellurique

Les variations du champ magnétique terrestre induisent dans le sol un champ électrique et, ce sol étant légèrement conducteur, il en résulte des courants électriques, dits telluriques, de très faible intensité. Par «effet de peau», ces courants sont d’autant plus atténués vers la profondeur que la conductibilité du sol est forte et la fréquence du champ élevée. Les nappes de courant circulant dans le sol créent un champ magnétique en surface, de telle sorte que les variations magnétiques effectivement observées sont modifiées par rapport à celles que l’on observerait au-dessus d’un sol infiniment résistant.

Entre deux prises de terre, un potentiomètre mesure l’équivalent d’une différence de potentiel qui représente la circulation du champ électrique entre les deux prises. Sur un sol plan, le champ tellurique est parallèle à sa surface, et deux «lignes telluriques» à angle droit le déterminent complètement. Des observatoires enregistrent continuellement ses variations qui ont, nécessairement, une grande parenté avec celles du champ magnétique.

Le champ tellurique provenant d’un phénomène d’induction est favorisé, toutes choses égales, par la fréquence des variations et, pour des pulsations magnétiques de faible amplitude et très rapides, certains trouvent plus avantageux de les étudier par voie tellurique.

Le rapport entre les amplitudes des variations magnétiques et celles des champs telluriques qui en résultent dépend de la conductibilité électrique du sous-sol. L’enregistrement simultané des deux variations permet d’obtenir des informations sur cette conductibilité: c’est le principe de la méthode de prospection magnéto-tellurique ^{[cf. GÉOPHYSIQUE]}.

Champ moyen et champ de variation

Partant des valeurs moyennes horaires des éléments magnétiques fournies par le dépouillement des magnétogrammes d’un observatoire, on passe à des valeurs moyennes journalières, mensuelles, annuelles, comme le fait un climatologiste pour les températures de l’air. Mais, alors que les moyennes annuelles des éléments météorologiques subissent des sautes irrégulières d’une année à l’autre, les valeurs moyennes des éléments magnétiques, que nous considérerons comme définissant un «champ moyen», sont pratiquement constantes; plus exactement, elles subissent une évolution continue et très lente au long des années et des siècles. Cette variation, dite séculaire, est une des caractéristiques essentielles du champ magnétique terrestre moyen. La dérive séculaire étant très douce, on peut, à partir de courbes donnant la variation des éléments d’année en année, dans un observatoire, définir le champ moyen à une époque quelconque qu’il suffit à un dixième d’année près; par exemple, «1984, 5» signifie «vers le 1^er juillet 1984».

À un instant bien déterminé, nous pouvons considérer le champ observé comme résultant de l’addition du vecteur champ moyen de l’époque, づ^m , quasi stationnaire et bien connu, et d’un champ, づ^v , d’intensité comparativement très faible, mais qui varie d’un instant à l’autre; c’est le «champ de variation». Cette définition, qui pourrait n’être qu’arbitraire, touche en réalité au fond des choses; il se trouve que le champ moyen et sa dérive séculaire résultent de causes situées à l’intérieur du globe, alors que le champ de variation, appoint très faible au champ moyen pour donner le champ instantané, provient, lui, de causes qui sont à l’extérieur du globe. Cette distinction, très simple, de champ moyen et de champ de variation a réellement séparé deux domaines en géomagnétisme, l’interne et l’externe.

Les définitions qui précèdent s’appliquent à un observatoire. Mais, sachant par expérience que le champ de variation est, en première approximation, le même à des centaines de kilomètres alentour, on peut, ayant mesuré le champ instantané en un lieu, en déduire le champ moyen à l’époque de la mesure. De plus, les dérives des éléments du champ moyen étant aussi sensiblement les mêmes entre des points peu éloignés, on peut, s’aidant de la connaissance de la variation séculaire dans les observatoires (et aussi en d’autres lieux où on la suit), passer du champ moyen à l’époque de la mesure à sa valeur à toute autre époque. On peut donc connaître le champ moyen en un grand nombre de points d’une région à une époque choisie, et établir ainsi un réseau magnétique.

2. Distribution du champ moyen

Réseaux magnétiques locaux

À l’échelle de l’hectomètre, le champ magnétique terrestre est pratiquement uniforme, en général. Mais, si le sous-sol proche présente des contrastes magnétiques (objets enterrés ou, beaucoup plus généralement, gisements de roches riches en minéraux magnétiques qui portent des aimantations rémanentes et, en tout cas, des aimantations induites par le champ terrestre même), l’uniformité disparaît: les valeurs d’un élément quelconque du champ moyen, déterminées en un réseau de points serrés, varient de station en station. L’interprétation de ces différences permet d’obtenir des informations sur la structure du sous-sol pour ce qui concerne ses propriétés magnétiques: c’est la technique de la prospection magnétique. Suivant la profondeur des structures recherchées, les mailles du réseau doivent être plus ou moins larges: de l’ordre du mètre en prospection archéologique, de l’hectomètre en prospection minière, de la dizaine de kilomètres en prospection pétrolière de reconnaissance, qui est toujours aérienne maintenant.

Il est intéressant de connaître l’ordre de grandeur des anomalies naturelles possibles, en entendant par «anomalie» la différence entre le champ moyen observé sur la structure et le champ normal de la région. Au-dessus de masses de terre cuite enterrées (restes de fours ou foyers, tessonnières, murs de briques), on peut observer des anomalies de F atteignant une centaine de gammas. Au sommet du puy de Dôme, la déclinaison varie de 6 degrés sur 150 mètres. Dans l’avant-pays pyrénéen, des masses souvent invisibles d’une roche volcanique, l’ophite, remontée dans des venues diapiriques, peuvent donner sur des surfaces d’étendue très variable des anomalies, inattendues, de l’ordre de 1 000 gammas. Enfin, dans des régions volcaniques, au voisinage de points foudroyés, la roche a été aimantée par le champ magnétique intense produit par le courant électrique correspondant au coup de foudre (son intensité se compte en dizaines de milliers d’ampères), et les anomalies peuvent être énormes, mais sur des surfaces limitées.

Réseau magnétique de la France

Jusqu’à ces dernières années, le réseau magnétique français le plus complet correspondait à l’époque 1924, 0 et avait été obtenu par des mesures de trois éléments (D, I et H) en plus de 1 300 stations. Des cartes avaient été publiées relatives aux sept éléments du champ, les éléments non mesurés ayant été calculés; sur ces cartes étaient tracées des lignes «isomagnétiques» de l’élément considéré, lignes joignant les points où l’élément avait la même valeur ronde. Les isomagnétiques de D et de I sont couramment appelées respectivement isogones et isoclines.

L’élément D était mesuré à l’époque avec une bonne précision, aussi la carte des isogones était-elle assez exacte. Cette carte, qui est la plus demandée par les usagers, a été remise à jour de temps en temps par l’Institut géographique national et publiée dans l’Annuaire du Bureau des longitudes , en tenant compte de la variation séculaire de D, déterminée à l’Observatoire français ainsi qu’en un certain nombre de stations visitées à intervalles réguliers (réseau de répétition). Il faut reconnaître que ces mises à jour successives l’avaient un peu déformée à la longue. Les cartes de I et H, déjà moins sûres, étaient acceptables, mais celles de Z et F étaient très imprécises, le calcul de ces deux éléments entraînant un cumul des erreurs faites sur I et H. Sur chaque carte, les isomagnétiques ont une certaine orientation générale: approximativement sud-nord pour D et ouest-est pour les autres éléments; les variations d’une extrémité à l’autre du territoire français sont appréciables: diminution de l’ordre de 6 degrés pour D, de l’ouest à l’est; augmentation de l’ordre de 7 degrés du sud au nord pour I; la composante H diminue du sud au nord et les éléments Z et F augmentent, ces variations présentant des gradients se comptant en gammas par kilomètre. Les lignes isomagnétiques sont sinueuses et, dans certaines régions, elles sont très déformées; on dit qu’il s’agit d’anomalies régionales. C’est le cas des zones anciennes encadrant les grands bassins sédimentaires; une grande anomalie qui s’étend de la Seine-Maritime au Nivernais surprend un peu; son explication, qui n’est pas encore clairement établie, doit être cherchée dans la structure profonde du Bassin parisien.

Récemment, d’une part parce que le réseau magnétique français était devenu insuffisant, d’autre part pour contribuer à la grande opération du «réseau magnétique mondial», de nouvelles mesures ont été exécutées sur toute la France et ses bordures océaniques. C’est un réseau partiel, puisqu’il n’a porté que sur un élément, l’intensité totale F; mais elle a été mesurée en avion avec un magnétomètre à vapeur de césium, c’est-à-dire, cette fois, avec une grande précision. L’avion volait à une altitude de 3 000 m (sauf sur la région alpine), décrivant des lignes sud-nord qui étaient espacées régulièrement de 10 km et sur lesquelles la mesure était pratiquement continue. Beaucoup de précautions avaient été prises pour assurer une altitude constante de vol, un repérage continu de la position géographique de l’avion, une bonne réduction des observations (l’opération se faisait par éléments d’un quadrillage et un magnétomètre analogue à celui qui était remorqué par l’avion fonctionnait au sol, vers le centre du carreau concerné).

La carte obtenue a été publiée à l’échelle du millionième. Les isomagnétiques de F, rapportées à l’époque 1964, 5 y sont tracées de vingt en vingt gammas. La figure 2 représente une version allégée avec des courbes de cent en cent gammas. On y retrouve les caractères annoncés: augmentation de F en allant du sud vers le nord, gradient général de l’ordre de trois gammas par kilomètre et existence de régions d’anomalies dont celle du Bassin parisien. Contrairement à ce qu’on pourrait craindre, une telle carte, correspondant à l’altitude de 3 000 m, est bien plus intéressante que celle qui aurait été obtenue – au prix de quel travail! – par des mesures au sol. Le changement d’altitude n’entraîne qu’une faible diminution générale de F; et surtout, il en résulte un étouffement de toutes les anomalies locales et un adoucissement de l’effet de détail des structures régionales. Le réseau aérien donne une vue plus large et, finalement, plus exacte des structures magnétiques liées à la structure géologique de chaque région.

À partir du réseau magnétique, une carte des anomalies régionales de F a été tracée, sur laquelle des teintes de plus en plus accentuées marquent les zones de plus grande anomalie positive ou négative. En réalité, le problème est difficile car il faut arriver à décrire un champ régional dont les variations dans toute la surface couverte ne proviennent que de causes d’origine très profonde, les anomalies (différence entre F observé et ce F en quelque sorte théorique) devant décrire, elles, l’effet de structures situées dans la croûte et le manteau supérieur.

Mais l’exploitation des données accumulées n’en est pas restée là. S’appuyant sur le fait qu’un champ magnétique n’est pas une grandeur quelconque, mais que ses variations dans l’espace doivent satisfaire des relations bien définies, il a été possible d’en déduire les variations des autres éléments. La figure 3 représente la carte de la déclinaison (pour 1965, 0) à l’altitude 3 000 m, obtenue à partir du réseau de F et aussi de mesures précises du vecteur づ en une trentaine de stations au sol. Une telle opération conduisant à la connaissance de la direction du champ par la mesure de son module peut paraître paradoxale; elle a mené, pourtant, à un résultat certainement plus précis que celui que l’on aurait obtenu en mesurant D directement avec un magnétomètre vecteur aéroporté. La carte de D, si habilement obtenue, est pratiquement valable au sol avec l’avantage, signalé pour la carte de F, d’un adoucissement des irrégularités locales.

Réseau magnétique mondial

La couverture magnétique de la surface du globe est extrêmement hétérogène. Les réseaux magnétiques nationaux, exécutés à des dates dispersées, avec des densités de stations et des précisions de mesures dissemblables, n’en couvrent qu’une faible surface. Plusieurs missions dans les contrées déshéritées, les régions polaires en particulier, ont complété, tant bien que mal, la connaissance du champ moyen sur les continents. Sur les océans, des campagnes de mesures ont été organisées, mais elles ont souvent un défaut de précision portant sur les mesures elles-mêmes, sur la position géographique du navire et bien entendu sur la réduction qui ne bénéficie pas d’observatoires proches. Les campagnes du navire américain Carnegie (disparu en 1929) sont célèbres; les campagnes, plus récentes, du navire soviétique Zarya sont aussi très importantes. Une grande opération concertée à l’échelle mondiale, à laquelle il a été fait allusion à propos du réseau français, a eu lieu au début des années soixante-dix avec des mesures au sol et en mer et avec des campagnes très étendues de mesures aériennes.

À cela s’ajoutent les énormes difficultés rencontrées pour rassembler les données acquises et pour les réduire à une époque donnée. Cette opération avait été reprise à l’Institution Carnegie de Washington avec réduction à l’époque 1945, 0. Des cartes très détaillées de trois éléments et des cartes réduites de tous avaient été publiées et reproduites dans toutes sortes de publications et d’ouvrages. La figure 4 représente une carte, un peu idéalisée, de l’inclinaison magnétique sur toute la surface du globe. Sur une telle carte de I, l’isocline 0 (inclinaison nulle) court dans les régions équatoriales: elle est dite « équateur magnétique ». Vers le nord de cette ligne, l’inclinaison est positive et elle croît assez vite, puis de plus en plus lentement, pour tendre vers + 90⁰ (direction sud-nord magnétique vers le bas). Ce point est dit pôle magnétique nord ou, pour être plus précis, pôle nord d’inclinaison; il est situé dans le Grand Nord canadien. Au sud de l’équateur magnétique, la direction horizontale du champ reste bien, en gros, du sud vers le nord, mais l’inclinaison est négative, c’est-à-dire la pointe nord de la boussole est sollicitée vers le haut; la valeur absolue de I croît quand on s’éloigne vers les régions polaires australes, et on atteint le pôle sud d’inclinaison situé près de la terre Adélie sur le continent antarctique. On remarquera que, sur l’équateur géographique, l’inclinaison est déjà fortement boréale en Amérique du Sud, alors qu’elle est fortement australe en Afrique.

Parmi les autres cartes, on ne retiendra que celle de D (fig. 5), souvent remise à jour pour les navigateurs. Elle est d’apparence compliquée parce que les isogones, d’après la définition même de D, rayonnent autour de deux points dans chaque hémisphère, le pôle géographique et le pôle d’inclinaison. Dans les régions polaires, la déclinaison peut prendre toutes les valeurs de 0 à 180⁰ est ou ouest, mais dans la plupart des régions habitées elle dépasse rarement 30⁰, c’est ce qui a conduit à ne pas la compter de 0 à 360⁰ comme les azimuts. Une ligne sinueuse remarquable court tout autour du globe, passant par les quatre pôles; entre les pôles géographique et magnétique d’un même hémisphère, elle est le lieu des points de déclinaison 180⁰; ses deux autres «segments», beaucoup plus longs, correspondent à une déclinaison nulle: ce sont les «lignes agoniques», qui séparent les régions aux déclinaisons de signe contraire.

Analyse mathématique du champ mondial; champ de Gauss

Partant de la connaissance de la répartition des éléments du champ moyen à la surface du globe, on peut s’élever à une formule donnant le potentiel magnétique dont il dérive, en fonction de la latitude, de la longitude et de la distance du point au centre de la Terre. La technique de l’analyse sphérique harmonique a été génialement appliquée au champ magnétique terrestre par Gauss. La formule est une somme de termes qu’il faut calculer un à un, ce qui était un énorme travail, et Gauss s’était limité à 24 termes. Actuellement, une telle analyse est faite sur ordinateur et, si l’établissement du programme reste laborieux, les calculs sont très rapides; on va couramment jusqu’à plusieurs centaine de termes. De ce vaste ensemble qu’est l’analyse sphérique harmonique du champ magnétique terrestre moyen d’une époque donnée, on ne retiendra que les conclusions principales, celles de Gauss, confirmées par de nombreuses analyses ultérieures:

– Le champ moyen provient de causes situées à l’intérieur du globe, et la contribution du champ de variation se trouve en moyenne nulle.

– Le premier terme du développement correspond à un champ extrêmement simple, analogue à celui que donnerait un dipôle (c’est-à-dire un aimant de petit volume) situé au centre de la Terre, et dont le moment magnétique M^t serait dirigé suivant l’axe de rotation de la Terre (dipôle centré axial). Un tel champ est évidemment de révolution, c’est-à-dire identique en tous points d’un même cercle de latitude, et, étant la colatitude d’un point quelconque situé à la distance r du centre de la Terre, ses deux composantes H^r , radiale (ce qui revient à dire verticale), et H^t , horizontale, dans le plan méridien du lieu, ont pour valeurs:

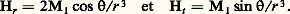
Pour un tel champ, la déclinaison magnétique est donc nulle partout, et l’inclinaison I est liée à la colatitude par la relation:

– Les trois premiers termes, pris ensemble, correspondent encore à un dipôle centré, de moment M, mais dont la direction est oblique par rapport à l’axe de rotation terrestre; c’est le dipôle de Gauss caractérisé par la colatitude ⁰ et la longitude 﨏⁰ du point appelé pôle de Gauss, où l’axe du dipôle rencontre la surface du globe, et par la valeur M du moment magnétique. Actuellement, le pôle nord de Gauss ou «pôle géomagnétique» a pour coordonnées: ⁰ = 11,5⁰ et 﨏⁰ = 69⁰ ouest; il est situé vers l’extrémité nord-ouest du Groenland; le pôle géomagnétique sud est évidemment antipodal. Quant au moment, on l’exprime généralement en donnant la valeur de M/R³, R étant le rayon de la Terre; cette quantité, désignée par H⁰, vaut 0,315 Oe = 25 A/m. Un tel champ a la même structure que le précédent, mais il est incliné par rapport à l’axe du globe. Les relations indiquées pour le dipôle axial restent valables, mais n’est plus la colatitude géographique, c’est maintenant ce qu’on appelle la colatitude géomagnétique, distance angulaire du lieu considéré au pôle de Gauss; connaissant ⁰, on calcule facilement en un point donné P, en résolvant le triangle sphérique ayant pour sommets P, le pôle géographique et le pôle de Gauss. Le grand cercle normal à l’axe de Gauss est dit équateur géomagnétique; il est incliné de 11,5⁰ sur l’équateur géographique. Le champ y est minimal avec la valeur H⁰ à la surface du globe, et il est maximal sur l’axe de Gauss, avec la valeur 2 H⁰ au pôle de Gauss.

– Dans les trois premiers termes du développement de Gauss, la distance r est au dénominateur à la puissance 2; et cette puissance croît continuellement dans les termes suivants; il en résulte que, si r augmente, l’importance de tous les termes diminue, mais relativement moins vite pour les trois premiers. Ainsi, très loin de la Terre, le champ s’affine de lui-même et tend vers celui du dipôle de Gauss, qui représenterait, comme on disait jadis, le «champ cosmique» de la Terre. En réalité, les mesures magnétiques spatiales qui se sont développées à l’ère spatiale ont montré qu’il n’en est pas exactement ainsi: à cause de l’action du «vent solaire», ou expansion de la couronne solaire, le champ magnétique terrestre est déformé, ses lignes de force étant refoulées en quelque sorte du côté tourné vers le Soleil et étirées de l’autre côté. Finalement, l’action magnétique de la Terre se trouve confinée dans un volume dit magnétosphère ^{[cf. MAGNÉTOSPHÈRES]}, limité par une surface, la magnétopause, dont la distance moyenne, dans la direction du Soleil, est de l’ordre de 10 R. Malgré cette contrainte exercée par l’arrivée de particules solaires électrisées, le champ moyen à l’intérieur de la magnétosphère est donné avec une bonne approximation par le développement complet de Gauss, à partir duquel, par exemple, on définit des points «conjugués magnétiques» qui se trouvent aux extrémités d’une même ligne de force du champ moyen réel.

Dans la magnétosphère toujours, à une distance de quelques rayons terrestres, le champ moyen réel diffère assez peu du champ géomagnétique. Cela explique que tant de phénomènes géophysiques ont, sur le globe, une répartition à symétrie non géographique, mais géomagnétique; la concentration très marquée des aurores polaires dans chaque hémisphère autour d’une ligne quasi circulaire, le «cercle auroral», de colatitude géomagnétique un peu supérieure à 20⁰, est particulièrement remarquable à ce point de vue ^{[cf. AURORE POLAIRE]}.

Champ non dipôle

À la surface de la Terre, en un lieu quelconque, on connaît le champ moyen actuel d’après les cartes magnétiques récentes et, d’après ce qui précède, il est possible de calculer le champ géomagnétique. Par définition, le «champ non dipôle» en ce lieu est le vecteur différence entre les vecteurs champ réel et champ géomagnétique. Il est courant de l’exprimer par sa composante verticale Z^ND et sa composante horizontale で^ND (d’intensité H^ND et d’azimut 見). Ainsi, à Paris, on aurait Z^ND = 漣 6 970 塚, H^ND = 4 140 塚, 見 = 73⁰ (compté du nord vers l’est). La même opération étant faite pour un grand nombre de points de la surface du globe, on peut reporter sur une carte mondiale la valeur Z^ND et le vecteur で^ND en chacun de ces points. L’opération serait sans intérêt si ces grandeurs se distribuaient au hasard; or, il n’en est rien et l’on peut tracer des courbes iso-Z^ND qui s’emboîtent les unes dans les autres, formant de grandes régions à excès de Z(Z^ND positif), décroissant depuis une valeur centrale maximale (foyer), et d’autres régions analogues à déficit de Z. Mieux encore, les vecteurs で^ND se placent assez régulièrement normalement à ces lignes, convergeant vers les foyers positifs de Z^ND et divergeant des foyers négatifs. Tout se passe comme s’il s’agissait de grandes anomalies mondiales, que l’on schématiserait assez bien au moyen d’une dizaine de dipôles radiaux, régionaux en quelque sorte, situés à grande profondeur, par exemple à la limite noyau-manteau, les uns dirigés vers l’intérieur (donnant les Z^ND positifs), les autres vers l’extérieur.

Il est intéressant de considérer l’ampleur du champ non dipôle: il ne constitue pas un petit appoint au champ dipôle, mais il en est parfois une fraction importante. Par exemple, Z^ND atteint + 16 000 塚 (0,16 Oe), dans la grande zone positive qui s’étend sur l’Eurasie, et 漣 15 000 塚 sur l’Atlantique, à l’ouest de l’Afrique centrale; les valeurs de H^ND peuvent dépasser 10 000 塚.

3. Variation séculaire du champ moyen

D’après les observations directes

Dans tout observatoire, comme il a été dit plus haut, on assiste à une dérive lente des éléments du champ moyen d’année en année, se poursuivant au long des siècles, et cette «variation séculaire» est suivie en beaucoup d’autres lieux, par répétition de mesures. Par accord international, cette répétition est recommandée de cinq ans en cinq ans, ce qui a été fait en France depuis 1947 en quatorze stations (depuis lors, ce nombre a augmenté). On connaît donc, en un grand nombre de lieux (malheureusement situés presque exclusivement sur les continents), les taux annuels de variation des éléments; par exemple, en France, pour D, ce taux est de 6 par an, mais il varie assez fortement à l’échelle des décennies. Pour une époque donnée et pour un élément magnétique donné, on peut reporter sur une carte mondiale les valeurs du taux annuel de variation. Là aussi, on n’obtient pas une répartition désordonnée, et les courbes d’égale valeur qu’on appelle des « isopores » forment de grandes régions organisées, à taux positif ou négatif. De telles cartes, pour chaque élément et pour différentes époques à partir de 1900 environ, existent dans tous les traités de géomagnétisme. Nous ne retiendrons que les ordres de grandeur des taux maximaux observés: pour D on peut atteindre 15 par an dans un sens ou dans l’autre et, pour F, 150 塚.

Échappant aux détails que donnent les cartes d’isopores, on a une vue plus large de la variation séculaire en scindant le champ mondial en ses parties dipôle et non dipôle. Le dipôle, déterminé par Gauss pour l’époque 1835, a été ensuite maintes fois calculé. La conclusion générale est que la direction du dipôle de Gauss n’a pas varié d’une façon significative depuis un siècle, ce qui n’implique nullement sa fixité; au contraire, la valeur du moment M du dipôle a décru continuellement avec un taux relatif important, de l’ordre de 1/2 500 par an.

En ce qui concerne le champ non dipôle, les données sont insuffisantes pour le définir avant l’époque des grandes campagnes de mesure sur les océans. Un travail étendu (Bullard, 1950) a porté sur la comparaison de cartes dressées pour les époques 1907, 5 et 1945, 0; le détail des changements est compliqué, mais, en les idéalisant un peu, l’auteur conclut à un champ non dipôle, constant en structure et intensité, mais dérivant d’est en ouest à la vitesse de 0,18 degré par an. Il faut considérer qu’il s’agit là d’un résultat incertain et, en tout cas, établi sur une durée beaucoup trop courte, et ne pas se laisser aller à penser que tout se passe comme si le champ non dipôle était vraiment une structure permanente tournant dans le sens est-ouest autour du globe à raison d’un tour tous les 2 000 ans!

Ainsi, la connaissance de l’évolution de l’ensemble du champ terrestre est très vite bornée vers le passé; on peut seulement espérer obtenir une idée de l’ampleur possible de la variation d’après des séries d’observations assez étendues qui ont été faites en quelques lieux. Les séries de Paris et de Londres sont les plus longues en ce qui concerne la direction du champ; mais leurs données sur l’évolution de D et I, très bonnes depuis qu’il existe des observatoires (1840 à Londres, 1883 à Paris), acceptables jusque vers 1800 parce que des mesures fréquentes étaient faites alors, deviennent de plus en plus rares et imprécises, et aucune d’elles ne remonte au-delà du XVI^e siècle. Un fait intéressant apparaît pour toute la période de 1800 à nos jours: les courbes de variation pour Paris et pour Londres sont analogues avec un certain décalage; par exemple l’inclinaison à Londres est de deux degrés supérieure à celle de Paris. Il est courant de représenter à la fois les variations de D et I en un lieu par un graphique, comme celui de la figure 6 relative à Paris; on peut y lire l’ampleur totale de la divagation de D et I, durant les quatre derniers siècles (courbe définie par les points réunis par des tirets): D a atteint les valeurs extrêmes 10⁰ est environ et 22⁰ ouest, I les valeurs 64⁰ 30 et 74⁰. On voit que, si la dérive séculaire est lente, la divagation totale peut être forte; non seulement la boussole n’indique pas le nord géographique, mais son écart avec cette direction n’est pas constant; la boussole de Napoléon, par exemple, pointait, à Paris, vers 22⁰ à l’ouest!

Sur la figure 6, un fait est frappant, c’est une certaine régularité de la courbe qui rappelle les trois quarts d’un ovale. Cette constatation a eu un effet fâcheux dans beaucoup d’esprits, en suggérant l’idée que l’ovale se fermerait peu à peu, et même qu’il avait été parcouru antérieurement; la variation séculaire serait cyclique, avec une «période» d’ailleurs différente suivant les auteurs conquis par cette vue simpliste. Une telle idée, difficile à déraciner, est tout à fait erronée: d’une part, elle ne cadre pas avec les observations faites ailleurs sur le globe; d’autre part, elle sera complètement infirmée par ce qui va suivre.

Étude indirecte: archéomagnétisme

Une possibilité inattendue s’offre à nous de retrouver la direction et l’intensité du champ magnétique terrestre dans tout le passé accessible à l’archéologie, cela à partir d’aimantations rémanentes qu’il a laissées dans les terres cuites et, accessoirement, dans les coulées volcaniques. Ces corps, très hétérogènes, sont constitués principalement par des minéraux non susceptibles de rémanences, parmi lesquels se trouvent dispersés, en grains souvent très fins, des minéraux ferromagnétiques dont les principaux sont le sesquioxyde de fer, les ilménohématites et, surtout, les titanomagnétites avec leur chef de file, la magnétite. À condition d’en considérer un volume suffisant, de l’ordre du dm³ par exemple, ces corps placés dans un champ magnétique prennent une aimantation uniforme par une sorte de compensation statistique, bien que chaque grain soit très anisotrope. Mais ils ont une propriété très intéressante, celle d’acquérir un type de rémanence qui leur est propre, dite «aimantation thermorémanente», quand ils se refroidissent dans un champ magnétique, ce qui est le cas général des terres cuites et des laves soumises au champ terrestre quand elles passent d’une température élevée à la température ordinaire après leur cuisson ou leur épanchement. Cette thermorémanence est acquise tout au long du refroidissement à partir du point de Curie le plus élevé de leurs minéraux magnétiques et, le corps étant revenu à la température ordinaire, elle est très résistante, dure magnétiquement si l’on veut. Par contre, un réchauffement la détruit avec une sorte de réversibilité, correspondant à ce qu’on a appelé la «mémoire magnétique des terres cuites»: un réchauffement à une température donnée fait disparaître l’aimantation qui s’était fixée pendant le refroidissement entre cette température et la température ordinaire. Il y a là des possibilités curieuses d’applications archéologiques: on peut, par exemple, retrouver les températures de recuit de terres cuites d’une construction incendiée ou de poteries remises au four pour fixer des colorations.

Mais revenons à la recherche du champ magnétique terrestre passé. Un reste de four (de potier, de verrier, à chaux...) ou de foyer, s’il est resté bien en place, continue à porter la thermorémanence qu’il avait acquise quand il s’est refroidi pour la dernière fois. La direction de l’aimantation est donc celle du champ de l’époque; mais il s’agit d’intensités d’aimantation très faibles qui ne peuvent être mesurées qu’au laboratoire sur des appareils qu’il a fallu créer pour cela et qui sont maintenant très précis. Alors, sur le terrain, on recueille des échantillons en repérant leur orientation; par exemple, on moule sur le bloc à détacher une masse de plâtre dont la partie supérieure a été façonnée en un plan bien horizontal, et, sur ce plan, s’aidant d’un théodolite visant le Soleil, on trace une ligne dont l’azimut est connu. La direction d’aimantation étant déterminée au laboratoire, on obtient la déclinaison et l’inclinaison du champ ancien. En général, plusieurs échantillons d’une même structure archéologique donnent des valeurs très voisines, et la précision obtenue est couramment de un degré sur I et de deux degrés sur D. Quelques difficultés se présentent du fait d’aimantations parasites possibles (aimantations visqueuse et causée par la foudre), mais leur effet peut être éliminé, ces aimantations étant magnétiquement «douces» par rapport à la thermorémanence.

Il s’agissait là de terres cuites demeurées en place depuis leur dernier refroidissement. Les briques d’une construction portent bien une thermorémanence acquise dans le four où elles ont été cuites, mais leur position à la cuisson est inconnue. Cependant, si la déclinaison magnétique est irrémédiablement perdue, on montre facilement que, à condition de travailler sur un lot nombreux (une vingtaine), on peut retrouver l’inclinaison magnétique avec une bonne précision. Or une grande construction est souvent plus facile à dater qu’un four ou un foyer, et les valeurs D et I obtenues n’ont d’intérêt que si une date archéologique sûre peut être obtenue (la datation au carbone 14 est beaucoup trop imprécise).

Ces études ont été très poussées en France, mais elles sont lentes à cause de la carence des matériaux bien datés à certaines époques. Pour l’inclinaison à Paris, la courbe de variation est à peu près complète depuis 50 ans av. J.-C. jusqu’à nos jours. De 69⁰ vers 漣 50, I est passé par les valeurs minimales et maximales successives suivantes: 53⁰ vers 150; 67⁰ vers 250; 57⁰ vers 300; 73⁰ vers 700; 60⁰ vers 1000, époque où des doutes subsistent; après un maximum encore mal défini, 53⁰ vers 1310 et 74⁰ vers 1725; nous sommes alors déjà à l’époque des mesures directes. La déclinaison est restée relativement faible, est ou ouest, durant les sept premiers siècles de notre ère, puis elle est devenue est de plus en plus forte jusqu’à un maximum de 27⁰ est vers l’an 1000, pour diminuer et redevenir ouest faible puis est, et l’on entre aussi dans la période des mesures directes. Le fait important est que, si l’on porte toutes ces valeurs D et I sur la figure 6, elles ne se placent absolument pas sur l’ovale des derniers siècles; la courbe qui part du centre de l’ovale vers 漣 50 et monte presque droit pendant 150 ans décrit ensuite des boucles assez compliquées qui se déroulent toutes très au-dessus et très à droite de l’ovale, qui n’est donc qu’un accident propre aux derniers siècles et à l’ouest de l’Europe. L’ampleur totale de la divagation est maintenant (à Paris) pour les deux derniers millénaires: pour D de 27⁰ est à 22⁰ ouest, soit 50⁰ environ; pour I de 53⁰ à 74⁰, soit une vingtaine de degrés.

Faut-il ajouter que ces mesures permettent en contrepartie la «datation magnétique» en archéologie? Cette datation possible et efficace à certaines époques reste nécessairement difficile pour les périodes durant lesquelles la direction du champ s’est retrouvée plusieurs fois la même. Il en est ainsi, en Europe de l’Ouest, pour une partie de la période gallo-romaine.

L’intensité de l’aimantation thermorémanente acquise par un corps qui se refroidit dépend de l’intensité du champ agissant et, pour des champs très faibles, elle lui est proportionnelle. Partant de la mesure des intensités d’aimantation, on peut retrouver l’intensité du champ, mais c’est un problème difficile; la technique mise au point en France, certes très laborieuse, est très sûre si elle est mise en œuvre avec un soin suffisant. Le premier résultat obtenu a surpris: l’intensité F du champ terrestre à Paris a décru depuis 600 av. J.-C., presque dans le rapport de 2 à 1, c’est-à-dire qu’au début de notre ère le champ, dans nos régions, était presque deux fois plus intense que l’actuel. Des mesures, maintenant nombreuses, effectuées à l’étranger, ont montré qu’il s’agissait d’un fait mondial. Coïncidence peut-être fortuite, le taux de décroissance du moment du dipôle de Gauss, depuis plus d’un siècle, est du même ordre. Cette décroissance a suscité nombre de discussions, en particulier à propos de la datation au carbone 14, et aussi sur les conséquences biologiques à prévoir d’une annulation – qui reste incertaine – du champ terrestre.

Un des intérêts, et non des moindres, de l’archéomagnétisme est d’ouvrir un champ d’action vraiment pluridisciplinaire entre archéologues et géophysiciens; le contact a pu être difficile, il est maintenant excellent.

4. Paléomagnétisme

En archéomagnétisme, partant de rémanences, dans les terres cuites surtout, on cherche à suivre le détail de la variation séculaire du champ magnétique terrestre durant la période historique. En paléomagnétisme, on part aussi de rémanences, dans toutes sortes de roches, et on explore le champ magnétique terrestre durant les temps géologiques; il ne peut plus s’agir, en général, de variation séculaire. Le champ magnétique terrestre fossilisé dans les roches va plutôt servir à résoudre des problèmes géologiques. Bien qu’il s’agisse dans les deux cas d’aimantations de roches et de temps géologiques, il faut distinguer deux chapitres assez indépendants: celui de l’inversion du champ et celui du paléomagnétisme proprement dit.

Inversion du champ magnétique terrestre

Inversion d’après les roches volcaniques

Les roches volcaniques portent des aimantations thermorémanentes acquises lors de leur refroidissement; une technique analogue à celle utilisée en archéomagnétisme permet de retrouver la direction du champ terrestre à l’époque de la coulée. Si l’on échantillonne nombre de coulées parmi les plus jeunes, on trouve des directions de champ dispersées autour de l’actuelle de quelques dizaines de degrés, dispersion qui est un peu celle que nous avons observée pour les deux derniers millénaires. En descendant plus bas dans le Quaternaire, on trouve des aimantations ayant des directions voisines de l’actuelle, mais dans le sens opposé; le fait est mondial, et on doit admettre que le champ terrestre tout entier était alors renversé par rapport à l’actuel. Descendant encore, dans le Pliocène, puis le Miocène, on trouve des époques de champ «direct» et des époques de champ «inverse» successives.

Le premier cas d’inversion a été découvert en Auvergne au début de notre siècle; mais l’idée trop surprenante n’a cheminé que lentement pendant des décennies et s’est vue condamnée, très péremptoirement, à plusieurs reprises. Enfin, unanimement (ou presque) acceptée à partir de 1950, elle est alors entrée dans une carrière des plus brillantes.

Les inversions étant reconnues nombreuses et mondiales, il était intéressant de préciser leur succession. Cela n’a commencé efficacement qu’à partir de 1963, quand des géomagnéticiens ont pu disposer de laboratoires équipés pour la datation de roches relativement jeunes par la méthode au potassium-argon. Assez vite, on a reconnu quatre grandes périodes, directes et inverses, dont la durée est de l’ordre du million d’années; elles ont reçu des désignations partout acceptées, qui sont: de Brunhes pour la plus récente, directe; de Matuyama pour la suivante, inverse; puis de Gauss, directe, et de Gilbert, inverse. Mais, rapidement, on s’est aperçu que des inversions passagères, que l’on a appelées des « événements », se sont produites au cours de ces grandes périodes, et leur liste s’est allongée peu à peu. Finalement, une échelle de périodes directes ou inverses successives a été établie, dans laquelle, par entraînement, on a conservé les quatre divisions initiales; dans son état actuel, car d’autres événements peuvent n’avoir pas encore été remarqués, elle est donnée sur la figure 7. Toujours sur des coulées volcaniques, on s’est intéressé à la phase de changement entre les deux états, de champ direct et de champ inverse. Ce «passage à l’inversion» pourrait être très bref, de 1 000 à 10 000 ans, pense-t-on. Jusqu’ici, des tentatives de mesure d’intensité du champ fossile n’ont pas permis de savoir si le moment magnétique du globe s’inversait alors en basculant ou si, hypothèse plus séduisante, il diminuait, passait par zéro et croissait. En fait, la Terre paraît ne s’être jamais trouvée complètement dépourvue de champ magnétique. On remarquera que l’échelle s’arrête vers 4,5 Ma (millions d’années); ce n’est pas faute de roches volcaniques plus anciennes, mais on admet que la cadence des inversions est telle que l’imprécision sur la datation devient trop grande pour les distinguer clairement.

Inversion dans les sédiments océaniques

Dans les grands bassins océaniques, loin des continents, la sédimentation est très lente et les longues carottes de sondage que l’on sait y prélever (certaines atteignent presque 30 m de longueur) correspondent à des durées de dépôt se comptant en Ma Or, l’étude magnétique de ces carottes a montré qu’elles portaient des rémanences et, pour chaque niveau, on peut relever une direction d’aimantation (une valeur de l’inclinaison seulement sur les carottes non orientées, ce qui est le cas général). À la vérité, on ne connaît pas bien le mécanisme de cette aimantation, où probablement se mêlent l’aimantation par dépôt (les particules magnétiques sont orientées par le champ terrestre dans leur chute) et l’aimantation dite chimique ou cristalline (celle des cristaux qui se construisent en présence d’un champ magnétique). Mais le fait qui a retenu l’attention est que ces aimantations sont successivement directes et inverses, avec des séquences analogues à celles qui sont observées dans les roches volcaniques; c’est-à-dire que des segments successifs de la carotte sont reconnus correspondre à tel ou tel événement catalogué dans l’échelle volcanique.

Un premier résultat est que l’on obtient ainsi une datation absolue des sédiments des couches supérieures, c’est-à-dire qu’on peut déterminer, dans chaque région sondée, la vitesse de sédimentation (loin des continents, elle peut être de l’ordre de 1 à 10 mm par millier d’années). Dès maintenant, pour de grandes surfaces océaniques, il existe des cartes d’«isopaques» donnant en chaque point l’épaisseur totale des sédiments accumulés, par exemple pendant l’époque de Brunhes, c’est-à-dire pendant 700 000 ans.

Avec de longues carottes, on dépasse de beaucoup le niveau correspondant à 4,5 Ma, fin de l’échelle absolue. On peut ainsi poursuivre au-delà la description des séquences d’époques directes et inverses dans une échelle de temps relative; admettant un taux de sédimentation constant, on parle encore en Ma, et l’échelle actuelle atteint 10,6 Ma, durée pendant laquelle on a dénombré jusqu’ici quarante-neuf intervalles de polarité.

Anomalies magnétiques sur les dorsales

L’étude des dorsales médio-océaniques ^{[cf. DORSALES OCÉANIQUES]} a pris un développement et une importance géophysique et géologique énormes. Le vaste réseau dont elles couvrent le globe sur une soixantaine de milliers de kilomètres, avec une superficie de l’ordre de celle des continents, est étudié par tous les moyens de l’océanographie géophysique. On ne retiendra ici que l’étude magnétique.

Si, avec des magnétomètres, à protons par exemple, on effectue des mesures continues de F sur des «profils» normaux à l’axe d’une dorsale, on trouve de fortes anomalies (atteignant 2 500 塚 vers l’axe de la dorsale, alors que sur la France elles ne dépassent pas 350 塚), alternant abruptement du positif au négatif. Et, propriété essentielle, ces profils magnétiques sont à peu près identiques d’un bout à l’autre de longs segments de la même dorsale (avec d’évidentes parentés entre dorsales différentes), et sur chaque profil on trouve une symétrie remarquable par rapport à l’axe de la dorsale, marqué par une anomalie positive maximale. C’est donc un fait d’observation que, tout au long d’une dorsale, il existe des bandes symétriques, alternativement marquées par des anomalies positives et négatives. L’idée qui s’est imposée (F. J. Vine et D. H. Matthews, 1963; cf. TECTONIQUE DES PLAQUES) est que la bande axiale de la dorsale correspond à une sorte de fente gigantesque par laquelle monte de la matière du manteau qui s’aimante dans le champ terrestre en se refroidissant, et qui se trouve entraînée sur un substratum s’écartant progressivement de l’axe de la dorsale. Ainsi, quel que soit le mécanisme de ces mouvements, la bande centrale d’anomalie positive correspondrait à la matière venue pendant la période de Brunhes, la bande étroite suivante, de part et d’autre, à anomalie négative, correspondrait à de la matière venue pendant la courte période inverse, depuis le début de l’époque de Matuyama jusqu’à l’événement Jaramillo, et ainsi de suite. On a pu montrer – peut-être parfois avec un peu de complaisance – que, sur presque toutes les dorsales, on pouvait expliquer les séquences d’anomalies proches de l’axe de la dorsale, d’après l’échelle absolue des inversions obtenue sur les roches volcaniques continentales. Cette datation des bandes successives permet de déterminer le taux d’expansion des fonds océaniques qui varie, suivant les dorsales, entre 1 et 4,5 cm/an.

Au taux moyen d’expansion de 2 cm/an, la matière venue il y a 4,5 Ma, fin de l’échelle volcanique, se trouve à 100 km environ de l’axe de la dorsale. Mais on trouve des anomalies alternées et nettes bien au-delà; de sorte que, comme on l’a fait avec les sédiments marins, on a pu prolonger l’échelle des inversions, avec des dates relatives, obtenues en posant que le taux d’expansion est constant. Avec beaucoup de hardiesse, cette échelle a été portée jusqu’à 75 Ma, période pendant laquelle on a reconnu 171 changements de polarité. Il faut signaler que, pour fixer les positions relatives des événements, une échelle spéciale a été adoptée, consistant à numéroter des anomalies successives, arbitrairement choisies, d’après leur forme, leur ampleur, leur largeur; cette échelle est tout à fait différente de celle des périodes de l’échelle volcanique: par exemple, l’anomalie n^o 5 correspond à 9,4 Ma, et c’est à l’anomalie n^o 31 qu’on atteindrait 75 Ma; au-delà – et on est alors au Crétacé – on trouverait une longue période de champ direct.

Durant les 75 derniers Ma, la fréquence des inversions serait restée du même ordre. Mais, si des successions de polarité sont bien observées dans toute l’échelle stratigrafique, leur cadence a été très différente suivant les époques: ainsi, au Crétacé moyen, on aurait une longue période de l’ordre de 25 Ma de champ direct; au Trias, les inversions semblent avoir été nombreuses, mais, au Permien, sur une durée de 50 Ma environ, la polarité serait restée constante (et inverse). L’«affolement à l’inversion» que nous observons durant les époques géologiques récentes pourrait être spécial aux dernières dizaines de millions d’années, et c’est une raison supplémentaire de méfiance contre toutes les tendances à l’extrapolation du comportement du champ magnétique terrestre.

Paléomagnétisme proprement dit: ses principes

Le paléomagnétisme, entièrement fondé sur la mesure d’aimantations rémanentes portées par les roches dans toute la série géologique, a pris un développement considérable à partir de 1950, parce qu’il a brusquement rénové les idées de dérive des pôles et des continents qui, après avoir considérablement agité les géologues et les climatologistes pendant le premier quart de notre siècle, en étaient arrivées à un discrédit à peu près total. Le fait majeur est que le paléomagnétisme prétend décrire les dérives avec ses seuls arguments, alors que les idées antérieures reposaient sur un amalgame d’observations géologiques diverses et paléoclimatiques.

Pratiquement, toutes les roches portent des aimantations rémanentes, parfois d’intensité extrêmement faible dans beaucoup de roches sédimentaires. Le paléomagnétisme s’est bâti au départ sur l’idée que ces rémanences dataient de l’époque de la mise en place de la roche et que leur direction représentait celle du champ terrestre à ce moment-là. C’était une vue commode, mais beaucoup trop simpliste. En effet, on peut déjà se poser des questions en ce qui concerne les mécanismes d’aimantation à l’origine; s’il est clair que les roches volcaniques ont acquis initialement une aimantation thermorémanente, l’origine de la rémanence dans les roches sédimentaires, évoquée à propos des sédiments marins, est beaucoup plus incertaine. De plus, des roches anciennes ont toujours subi des transformations de toutes sortes qui ont atteint leurs minéraux magnétiques; ces changements minéralogiques, l’effet des élévations de température et de pression éventuellement subies ont nécessairement modifié les aimantations originelles. Enfin, des rémanences postérieures se sont ajoutées de diverses manières, dont trois ont été mentionnées au passage: le traînage magnétique, l’effet de la foudre, l’aimantation par cristallisation. L’étude des mécanismes d’acquisition de ces aimantations, de leurs propriétés, des procédés permettant d’isoler certaines d’entre elles («nettoyage magnétique») constitue une véritable science, le «magnétisme des roches», dont les enseignements se sont peu à peu imposés. Actuellement, on tend à abandonner l’étude des époques antérieures au Cambrien qui, au départ, semblaient curieusement donner les résultats les plus clairs; les aimantations naturelles sont, maintenant, toujours soumises aux traitements de nettoyage, par action progressive de champs alternatifs et de recuits.

Admettons, avec les pionniers du paléomagnétisme, que les directions d’aimantation (corrigées éventuellement des rotations qu’elles ont pu subir du fait des plissements) représentent celles du champ; le fait d’observation fondamental (publications anglaises de 1954) est que, pour une époque géologique et une région données (le Trias en Angleterre), les rémanences ont une direction générale caractéristique (avec les deux sens possibles d’ailleurs), qui peut être très différente de celle du champ actuel; il s’agit là évidemment d’une direction moyenne, à l’échelle des millions d’années. Très vite, les géomagnéticiens anglais déterminèrent l’évolution de cette direction «supermoyenne» en quelque sorte, au cours des temps géologiques, et la trouvèrent assez régulière.

Cette observation d’une lente évolution de la direction générale du champ terrestre en serait restée là sans l’apport d’une idée sur laquelle s’est bâti tout le paléomagnétisme: celle d’un champ moyen dipôle axial. Plutôt que sur quelques bases théoriques assez vagues, elle repose sur le sentiment que l’ensemble du champ terrestre pris en moyenne sur des milliers d’années doit être débarrassé de sa partie non dipôle et que l’inclinaison actuelle, relativement faible, de l’axe dipôle sur l’axe de rotation de la Terre a dû varier et prendre toutes sortes d’orientations symétriques par rapport à l’axe terrestre et donc éliminées statistiquement pour un champ moyen sur des millions d’années. Mais alors, si le «champ moyen géologique» correspond à ce champ infiniment simple qu’est un champ dipôle axial, la connaissance de I et D moyens au Trias, en Angleterre (ou plus exactement en l’un de ses points auquel sont rapportées les données), permet de calculer les positions relatives de la surface de l’Angleterre au Trias et du pôle magnétique (identique, par hypothèse, au pôle géographique): D indique le grand cercle sur lequel se trouve le pôle, et I, par la relation: tg I 練 tg = 2, fournit , distance angulaire du pôle. Il revient au même de dire qu’on a défini la position de l’Angleterre par rapport au pôle par sa colatitude et son orientation, son attitude si l’on veut, par rapport à un grand cercle passant par l’axe des pôles et traversant l’Angleterre. L’hypothèse du champ moyen de dipôle axial et le fait expérimental de la variation de la direction du champ observée au cours des temps géologiques entraînent l’existence de changements très importants dans les positions relatives du continent considéré et du pôle terrestre.

Dès 1954, à partir des mesures d’aimantation dans leur pays, les géophysiciens anglais obtinrent la course du pôle, relative à l’Angleterre; elle était impressionnante: situé vers le centre des États-Unis au Précambrien déjà lointain, le pôle avait dérivé vers le sud et vers l’ouest, jusque dans le Pacifique et au-delà de l’équateur au Précambrien final, et il s’était approché peu à peu de sa position actuelle, en passant par le Japon et l’extrême est de la Sibérie. Il faut entendre qu’il s’agit de la position du pôle dessinée sur une figure sphérique, liée à l’Angleterre, sur laquelle on a laissé le dessin actuel de la surface du globe; le fait réel est le mouvement de l’Angleterre par rapport à l’axe du globe qui est le véritable repère; le paléomagnétisme n’a aucune prise sur l’orientation de cet axe dans l’espace.

Les géophysiciens anglais interprétaient leur résultat dans l’hypothèse de la dérive des pôles (polar wandering ); les continents ayant gardé une forme et une disposition sensiblement immuables, l’ensemble de la surface du globe aurait dérivé par rapport à l’axe terrestre. Dans ces conditions, les courbes de dérive relatives à tous les continents devaient se superposer. L’expérience, vite acquise par des mesures en Amérique du Nord, en Inde, en Australie, montrant qu’il n’en est pas du tout ainsi, on en est venu à l’autre hypothèse des géologues: la dérive des continents. Il faut maintenant considérer que chaque continent s’est déplacé, pour son propre compte, par rapport à l’axe du globe; chacun a sa courbe de dérive par rapport à sa surface et, si on dessine ces courbes sur la carte actuelle du globe, devenue tout à fait conventionnelle, ces courbes, entraînées chacune par leur continent, sont indépendantes.

Des années durant, des paléomagnéticiens, en nombre toujours croissant, ont multiplié les mesures d’aimantations naturelles sur tous les continents pour toutes les époques géologiques. Les conclusions étaient, pour chaque continent, la description de ses positions successives en latitude et en altitude (la longitude n’est plus définie sur une surface du globe se déformant). Elles permettaient des comparaisons intéressantes entre les positions paléogéographiques ainsi définies aux différentes époques et les observations géologiques et paléoclimatiques (existence de formations glaciaires, coralliennes, désertiques à ces mêmes époques). Ces comparaisons ont souvent été décevantes, d’abord parce que c’est là un problème difficile, et aussi parce que, avec la multiplication des mesures et le soin plus grand apporté dans l’étude de la qualité des aimantations, les «courses» souvent énormes reconnues pour chaque continent ont varié beaucoup. L’idée de mouvement plus ou moins régulier a disparu, et les synthèses récentes décrivent des phases de mouvements, tantôt très rapides, tantôt quasi stationnaires.

Dans les années soixante, une idée intéressante a été développée, reprenant, au fond, celle des géologues créateurs de la notion de dérive des continents: l’existence des «supercontinents», Laurasie et continent de Gondwana, qui auraient dérivé chacun puis se seraient divisés, donnant respectivement l’Amérique du Nord et l’Eurasie pour le premier, et l’Amérique du Sud, l’Afrique, l’Australie, l’Inde et le continent antarctique pour le second. Des études, conduites à l’aide d’ordinateurs, sur les relations de forme entre des continents se faisant vis-à-vis et capables de s’emboîter les uns dans les autres ont renforcé les bases de cette thèse. Prenons le cas simple de l’Amérique du Sud et de l’Afrique (dont la possibilité d’emboîtement est la plus connue) et supposons qu’elles aient dérivé longtemps ensemble, accolées (dans un ensemble plus vaste ou non, peu importe). Pendant toute cette période, la courbe de dérive du pôle, relative au bloc qu’elles forment, est unique. Si, à une époque donnée (le Permien supérieur dans le cas choisi), les deux continents se sont mis à s’écarter l’un de l’autre, leurs surfaces de référence sont alors séparées, mais, sur chacune, les portions allant jusqu’au Permien supérieur ont évidemment exactement la même forme, tandis qu’au-delà ces formes n’ont plus de relation directe. Alors, les courbes de dérive de chaque continent étant dessinées sur leur sphère de référence propre, si, amenant les dessins des continents à s’emboîter, on trouve une superposition des courbes jusqu’au Permien supérieur, la probabilité est très grande qu’ils aient été soudés tous les deux jusqu’à cette époque. Par ce biais, le paléomagnétisme atteindrait maintenant les positions des continents en longitude relative. Les efforts ont porté sur des essais de reconstitution complète des supercontinents, Laurasie et Gondwana, et même d’un continent unique initial, la Pangée de Wegener. C’est un problème difficile ou, s’il est traité avec complaisance, trop facile, étant donné la grande indétermination de toutes les courbes de dérive ^{[cf. GONDWANA]}.

La phase la plus récente en paléomagnétisme réside dans le traitement d’ensemble des faits concernant la dérive des continents et l’expansion des fonds océaniques, dont les vitesses se trouvent être du même ordre. Actuellement, on ne voit plus les continents labourant le fond des océans, mais, au contraire, portés par le mouvement d’expansion océanique (cf. LITHOSPHÈRE, SUBDUCTION, TECTONIQUE DES PLAQUES).

5. Théories sur l’origine du champ moyen

Une théorie complète de l’origine du champ moyen doit expliquer aussi sa variation séculaire et, en plus, maintenant, le phénomène d’inversion considéré comme une caractéristique très importante du champ. Depuis plus d’un siècle, de nombreuses théories ont été bâties, dont plusieurs se réduisent à la recherche du mécanisme de production du champ dipôle.

Une sphère uniformément aimantée produisant, à l’extérieur de sa surface, un champ équivalent à celui d’un dipôle centré, telle est l’image qui s’est d’abord imposée pour la Terre. L’accroissement de la température avec la profondeur entraînant, à quelques dizaines de kilomètres, le dépassement des points de Curie connus, l’aimantation devait être localisée dans une couronne sphérique limitée par la surface de la Terre et une surface isotherme correspondant au point de Curie maximal des minéraux magnétiques (670 ⁰C). De cette hypothèse, il ne reste rien, sinon l’explication des anomalies locales et régionales (correspondant à des surfaces petites à l’échelle du globe), qui sont bien dues à des aimantations de roches et qui restent fixes alors que les anomalies mondiales (champ non dipôle) dérivent.

D’autres théories ont fait appel à des causes électriques, par exemple à des courants de conduction créés à l’intérieur du globe à son origine et s’éteignant lentement, ou à des courants de convection dus à des charges électriques, entraînées par la rotation de la Terre, et qui se trouveraient séparées en charges d’ailleurs énormes, positives vers l’intérieur et négatives vers l’extérieur. D’autres théories encore se fondaient sur des phénomènes nouveaux; la plus récente, celle de Blackett (1947), qui a eu un succès énorme mais très éphémère, invitait à considérer que tout astre possède un moment magnétique proportionnel à son moment cinétique; les deux moments ayant même axe et des sens liés, cette hypothèse était en contradiction absolue avec le phénomène d’inversion.

Depuis quelques décennies, on en est venu à imaginer une circulation de courants électriques dans le noyau que la sismologie nous présente fluide et bon conducteur, les forces électromotrices étant dues à un «effet dynamo ». On admet l’existence dans ce noyau de courants de convection, d’origine thermique, qui peuvent être une des sources d’énergie nécessaires. Mais il faut expliquer le mécanisme créant les forces électromotrices par suite de ces mouvements. Une dynamo ordinaire est hétérogène avec des conducteurs et des isolants; le noyau, au contraire, est continu; il s’agit d’une dynamo homogène, très spéciale. Le problème complet, qui est de magnéto-hydrodynamique en milieu dense et qui a donné lieu à d’importants travaux, s’est montré jusqu’ici trop difficile. Seuls des problèmes partiels ont été résolus, en liaison vague avec le problème véritable; l’un d’eux a pu être traité théoriquement et expérimentalement et a montré au moins la possibilité d’un effet dynamo dans un milieu conducteur continu: il s’agit de deux sphères conductrices tournant dans un milieu conducteur; à partir d’un champ magnétique infime, accidentel, des courants électriques peuvent être produits dans le milieu et il en résulte un champ magnétique extérieur qui peut être intense. Un autre problème, plus éloigné encore du problème réel, a aussi été traité, c’est celui d’un système de deux dynamos couplées (mais non homogènes); le courant produit oscille irrégulièrement (ce qui rappelle les variations d’intensité du champ terrestre), puis s’inverse, soit brièvement (c’est l’événement dans le phénomène d’inversion), soit plus longtemps avec à nouveau des oscillations (ce qui serait l’équivalent de la période inverse). Mais il ne s’agit là que d’analogies.

Le problème s’est élargi quand on y a inclu le champ magnétique des planètes ; les mesures directes montrent que ce champ est nul ou très faible pour la Lune, Vénus et Mars, mais appréciable pour Jupiter, Saturne, Uranus et Neptune.

6. Le champ de variation

Nous abandonnons les échelles de la dizaine de millions d’années du paléomagnétisme, de la centaine de milliers d’années de l’inversion et du siècle de l’archéomagnétisme pour celles du jour, de la minute et de la fraction de seconde du champ de variation. Le document de travail est dans les magnétogrammes des observatoires, avec tous leurs détails qui avaient été éliminés complètement par la définition d’un champ moyen pris sur une longue durée. Les magnétogrammes lents, qui ont été de beaucoup les plus utilisés, révèlent des variations «régulières» – il faudrait dire «ayant une certaine régularité qui les rend à peu près prévisibles» – et des variations accidentelles, ou encore transitoires, pratiquement inopinées, caractéristiques de l’activité magnétique qui fait passer d’une situation magnétique «calme» à une situation «agitée». Sur les magnétogrammes rapides, on trouve ces variations, de très faible amplitude en général, que l’on désigne sous le nom de pulsations.

Ces phénomènes résultent de l’existence d’une haute et lointaine atmosphère ionisée baignant dans le champ magnétique terrestre, cet ensemble étant soumis aux rayonnements solaires: ondulatoire (visible, ultraviolet et X) et corpusculaire (vent solaire), qui ont chacun une partie normale et une partie accidentelle résultant principalement des éruptions chromosphériques. Ces causes (ionisation, champ magnétique et rayonnements divers) se retrouvent enchevêtrées dans chacune des particularités du champ de variation, dont l’observation et l’interprétation fournissent un moyen d’étude indirecte des milieux extérieurs. Une étude directe a commencé grâce aux fusées et aux véhicules spatiaux, et des progrès rapides ont marqué ces dernières décennies; malgré cela, les théories, maintenant satisfaisantes d’un point de vue qualitatif, sont encore imprécises sur de nombreux points.

Variations régulières: variations diurnes

La plus importante des variations régulières, connue depuis longtemps, est la variation diurne solaire, que l’on symbolise par S. Pour l’étudier, on définit, pour chaque élément magnétique, la variation diurne moyenne de chaque mois. Comme on le fait en climatologie pour la température, on calcule les valeurs horaires moyennes mensuelles, dont on retranche la valeur moyenne générale de l’élément pendant le mois, ce qui fournit des écarts horaires mensuels. La courbe représentant ces écarts en fonction de l’heure, ou courbe de variation diurne, pour l’élément et le mois considérés, est généralement lisse. Dans un observatoire donné (de latitude géomagnétique pas trop élevée), les courbes correspondant à un élément ont, de mois en mois, des allures voisines, et les écarts les plus élevés, en valeur absolue, se produisent pendant les heures de jour, la variation étant très réduite au milieu de la nuit. L’excursion totale entre les valeurs extrêmes, dite amplitude de la variation diurne de l’élément, évolue au cours de l’année et au cours du cycle solaire undécennal; les maximums sont en été pour la variation saisonnière, et au paroxysme d’activité solaire pour la variation undécennale. Cette amplitude, relativement très faible, est, en France, de l’ordre de la dizaine de minutes pour les éléments relatifs à la direction et de la dizaine de gammas pour les composantes. Ainsi, pour fixer les idées, l’amplitude de la variation diurne de la déclinaison à l’observatoire français de Chambon-la-Forêt peut varier entre 5 minutes, en hiver et en année de minimum d’activité solaire, et 15 minutes, en été dans les années de maximum solaire. C’est un phénomène pratiquement insignifiant pour les usagers de la boussole; il est au contraire très utile dans la recherche magnéto-tellurique, où l’on a besoin de variations de «périodes» très différentes, depuis de très courtes jusqu’à de très longues.

Pour suivre la variation diurne sur l’ensemble du globe, on est amené à distinguer la variation diurne des jours calmes S^q (q de quiet ) obtenue en ne considérant, chaque mois, que les cinq jours les plus calmes mondialement. Aux latitudes moyennes, cette variation S^q n’est pas très différente de celle qui a été définie en prenant tous les jours du mois, et que l’on désigne par S^a (a de all ); mais on peut considérer que S^q représente un phénomène pur, que l’activité magnétique vient troubler. Aux lattitudes moyennes encore, la variation S^q est sensiblement la même en tous points d’un même cercle de latitude, si les heures sont comptées en temps local. Dans tous les traités de magnétisme terrestre, on trouve des figures donnant les courbes de variation diurne de trois éléments, pour différentes latitudes (de 0⁰ à 60⁰) et différentes saisons géophysiques (été, hiver et époques équinoxiales). En choisissant une altitude, pour le moment arbitraire, par exemple 100 km, on peut calculer une répartition de courants électriques, fixe par rapport à un observateur solaire, qui rendrait compte des faits observés. En réalité, l’analyse sphérique harmonique appliquée à la variation observée au sol a montré que les deux tiers du phénomène étaient dus à des causes externes, le reste provenant de causes internes qui sont les courants telluriques induits. On trouve aussi dans les traités des figures représentant ces nappes de courant, en principe conventionnelles, tracées pour les périodes d’équinoxe (elles sont alors symétriques par rapport à l’équateur géographique) et pour les périodes solsticiales (elles sont dissymétriques, les courants les plus intenses étant au-dessus de l’hémisphère qui est en été). Des mesures directes, non encore très significatives, ont montré que des nappes de courant existaient vers une centaine de kilomètres (peut-être avec d’autres nappes à un niveau plus élevé), de sorte que le système de courants calculé serait proche de la réalité.

Cependant, les courbes de variation diurne publiées pour les latitudes ne dépassant pas 60⁰ et les nappes de courant qui les expliquent sont tout à fait fausses dans les régions équatoriales sur lesquelles on les avait extrapolées. On s’est aperçu que, dans les régions de basse latitude, la variation diurne de la composante horizontale pouvait être près de trois fois supérieure à celle prévue d’après les nappes. L’étude de cette particularité a été très poussée depuis une vingtaine d’années, et on a montré qu’il fallait ajouter aux nappes anciennes une bande de courant électrique, relativement très intense sur l’hémisphère éclairé, s’étendant sur une largeur de quelques degrés de latitude le long de l’équateur magnétique: c’est ce qu’on a appelé l’«électrojet équatorial», par analogie avec les jets des météorologistes. On remarquera qu’il y a non seulement un renforcement puissant des nappes de courant classiques, mais une distorsion, le jet n’étant pas du tout le long de l’équateur géographique mais le long de l’équateur d’inclinaison.

Vers les latitudes élevées, la variation diurne prend un caractère très différent de celui qui a été décrit pour les latitudes moyennes, caractère qui s’accentue d’autant plus qu’on se rapproche de la zone aurorale. Là, les phénomènes dépendent de la position de la station par rapport à cette zone, qui correspond aussi à un électrojet puissant, mais fonction de l’activité magnétique; la symétrie des phénomènes est alors plutôt géomagnétique. La variation diurne des régions aurorales, qui prend des amplitudes anormalement fortes, n’est pas la suite du phénomène des latitudes moyennes; c’est beaucoup plus un phénomène d’activité magnétique qui peut retentir jusqu’aux latitudes plus basses, pour modifier la variation diurne S^q .

En ce qui concerne l’origine de la variation S^q , on pourrait penser à un effet de la déformation des lignes de force du champ terrestre par le vent solaire, déformation fixe pour un observateur solaire; l’effet existe, mais il ne représente qu’une faible partie du phénomène observé. Pour l’essentiel, il est admis, depuis longtemps, que la variation diurne est due à un mécanisme dynamo dans la haute atmosphère. Celle-ci est soumise à des mouvements, des vents, causés principalement par les actions gravifique et thermique du Soleil, et ce double effet de marée a tendance à produire un état de régime fixe pour un observateur solaire. Dans les masses d’air en mouvement dans le champ magnétique terrestre se produisent des forces électromotrices d’induction, qui, dans la haute atmosphère, conductrice à cause de son ionisation, provoquent des courants que les nappes doivent représenter. Plusieurs faits d’observation viennent s’insérer dans la théorie, par exemple: le «crochet magnétique» ou S.F.E. (solar flare effect ), renforcement passager de la variation diurne, concomitant de phénomènes puissants dans l’ionosphère, dû à une augmentation de l’ionisation durant une éruption chromosphérique; et l’effet des éclipses solaires entraînant au contraire une réduction d’ionisation. La théorie relative à l’électrojet équatorial paraît maintenant satisfaisante; elle fait intervenir la conductibilité transversale de Hall dans le cas particulier où le champ est horizontal (équateur magnétique). Cependant, une théorie complète de la variation diurne n’existe pas encore, à cause surtout de la difficulté de connaître les marées de la haute atmosphère.

Dans la variation diurne solaire, la position du Soleil joue un triple rôle par son action gravifique, thermique et ionisante. La Lune ne peut avoir qu’une action gravifique qui, ainsi, serait plus simple. On a depuis longtemps recherché une «variation diurne lunaire», c’est-à-dire de période 24 h 50 mn environ, en découpant le temps en jours lunaires. On trouve alors, comme on peut s’y attendre, une variation semi-diurne de très faible amplitude, plus forte cependant dans les régions équatoriales. Les phénomènes sont plus clairs si l’on considère séparément des jours lunaires à différentes étapes de la lunaison: une partie du jour lunaire correspond alors à des périodes de jour terrestre et une partie à des périodes de nuit terrestre. La variation, encore semi-diurne, présente des amplitudes très différentes dans ses deux oscillations; celle correspondant à la période de jour, c’est-à-dire à une atmosphère plus ionisée, est beaucoup plus ample. L’effet lunaire est analogue pour les deux demi-journées, mais agit sur des atmosphères de conductibilités très différentes.

Variations irrégulières: activité magnétique

Si les variations diurnes, solaire et lunaire, existaient seules, les courbes enregistrées sur les magnétogrammes seraient toujours très lisses. Cette situation est fréquente, et on est alors en situation magnétique «calme». Mais, souvent aussi, les courbes sont irrégulières, les écarts plus grands et les changements plus rapides; la situation est alors «agitée», et il y a tous les degrés entre une agitation faible et celle qu’on appelle «orage (ou tempête) magnétique», qui est exceptionnelle, mais se déclenche plusieurs fois par an en moyenne.

L’activité magnétique est étudiée de deux manières très différentes, conduisant chacune à des possibilités, différentes aussi, de traitement statistique: ou bien on considère l’agitation dans son ensemble et l’on essaie de qualifier son degré, dans un intervalle de temps donné, par un «indice d’activité magnétique»; ou bien on distingue des types d’agitation, des «individus», si l’on veut, dont on relève ensuite les occurrences au long des années.

Indices d’activité magnétique

Les deux indices de beaucoup les plus utilisés sont l’indice C, le plus ancien, et l’indice K.

Avec l’indice C, la période considérée est le jour, pris en temps universel, de 0 à 24 h T. U. On notera que si les variations diurnes sont «synchrones» en temps local, les variations correspondant à l’agitation magnétique sont, en général, synchrones vraies, c’est-à-dire en temps universel. L’indice C d’un jour, dans un observatoire, résulte du simple examen du magnétogramme correspondant dont le taux d’agitation est noté 0, 1 ou 2 (0 pour calme ou presque calme). On s’efforce de définir, non un taux absolu d’agitation, mais un taux relatif en faisant en sorte, dans chaque observatoire, que les nombres de fois où chaque indice est donné soient du même ordre. En effet, et c’est un fait important de l’agitation magnétique, elle est, au même moment, beaucoup plus forte vers les régions aurorales qu’aux latitudes moyennes. À ces latitudes au moins, l’agitation magnétique tend à être du même ordre partout sur le globe, et l’on peut parler d’un indice mondial d’activité. Cet indice Cⁱ (i pour international ) est obtenu pour chaque jour par moyenne des indices de chaque observatoire, rassemblés par l’institut météorologique de De Bilt. L’indice Cⁱ est catalogué pour tous les jours depuis 1884.

On peut reprocher à l’indice C son caractère trop subjectif. On lui préfère l’indice K, établi à partir de 1938, qui est plus objectif et plus détaillé. Attribué à des intervalles de trois heures, c’est un chiffre de 0 à 9, déterminé pour trois éléments en mesurant l’excursion maximale de l’élément dans l’intervalle considéré et en la traduisant en indice au moyen d’une échelle conventionnelle quasi logarithmique. Comme pour l’indice C, il faut tenir compte des variations de l’ampleur de l’activité avec la latitude (plutôt géomagnétique). Dans l’échelle type, l’indice 9 est donné à partir d’une «amplitude» de 500 塚; suivant les observatoires, on adapte l’échelle, proportionnellement, en prenant des limites pour l’indice 9, qui vont de 350 塚 à 2 500 塚. L’échelle type est la suivante:

En réalité, en cas d’activité nulle, on aurait dans chaque intervalle de trois heures une excursion due à la variation diurne; on l’élimine en considérant les écarts par rapport à la courbe de variation diurne plus ou moins idéalisée pour chaque jour. Des trois indices obtenus pour chaque intervalle de trois heures, on retient le plus élevé. Un jour (T. U.) donné est ainsi caractérisé par huit indices successifs. Comme pour l’indice C, on définit un indice mondial K^p , dit ici «planétaire», obtenu à partir des indices de douze observatoires choisi à des latitudes géomagnétiques peu élevées, et cet indice K^p est régulièrement publié. Des critiques se sont élevées contre le choix des observatoires (onze sont dans l’hémisphère Nord), et on trouve maintenant deux indices, K^N et K^S, établis séparément pour les hémisphères Nord et Sud.

Les indices locaux C et K, connus sur de longues durées, ont permis de rechercher les caractères statistiques de l’activité magnétique globale dans chaque région. Sa variation diurne, suivie avec K, présente sur presque tout le globe un maximum vers le milieu de la nuit; c’est l’inverse (maximum de jour très marqué) dans les calottes intérieures aux deux cercles auroraux. La variation saisonnière est semi-annuelle avec ses maximums aux équinoxes; la situation est, là encore, spéciale dans les calottes aurorales où la variation est annuelle avec un maximum très marqué l’été. Ainsi, le fait est à noter, l’activité magnétique dans les régions aurorales, par son intensité et ses caractères, est un phénomène nettement différent de l’activité générale sur le globe. La variation undécennale suivie avec l’indice K^p montre une relation entre K^p et l’indice d’activité solaire, mais avec un net décalage, l’activité magnétique restant forte pendant une partie de la phase décroissante de l’activité solaire. Enfin, l’activité magnétique suivie de jour en jour montre une certaine «récurrence de vingt-sept jours»: les périodes de forte agitation (ou aussi bien de calme magnétique) tendent à se répéter après vingt-sept jours, et cela parfois pendant des années. Cette durée est celle de la révolution synodique du Soleil, et on est conduit à penser à des phénomènes déclenchés, à chaque rotation, par le passage de structures de la surface solaire qui ne sont pas bien identifiées encore et qu’on se contente d’appeler des M-régions.

On a été conduit, depuis longtemps, à penser que l’activité magnétique générale, celle qui est mesurée par l’indice K^p , provient d’émissions de particules électrisées solaires, et on les considérait comme accidentelles. On a reconnu maintenant l’existence d’un courant continu de telles particules, le vent solaire, et l’activité magnétique est attribuée à des renforcements passagers de ce vent solaire. On a montré récemment qu’il y aurait une corrélation étroite entre l’indice K^p et la vitesse du vent solaire mesurée directement par des véhicules spatiaux.

Les phénomènes de l’agitation magnétique

On considère un certain nombre de types d’agitation, dont le plus intéressant est l’orage magnétique à début brusque. C’est une période de forte agitation qui s’étend sur un temps relativement long, de un à plusieurs jours, les orages les plus intenses ayant en général les durées les plus courtes. C’est un phénomène mondial dont le déroulement varie suivant les lieux pour un orage donné et varie d’un orage à l’autre, gardant cependant une allure générale commune, surtout si l’on s’en tient aux stations éloignées des régions aurorales.

Par situation magnétique calme ou un peu agitée, les éléments magnétiques changent subitement de valeur: des minutes (pour D) ou des dizaines de gammas (pour H et Z), en quelques minutes de temps. Sur les magnétogrammes lents, cette variation, qui atteint plus ou moins les différents éléments, apparaît comme un décrochement (fig. 1) sur les courbes enregistrées; c’est le début brusque ou S.S.C. (storm sudden commencement ). Le changement est particulièrement net sur H (composante horizontale), et il est presque toujours dans le sens d’une augmentation. Mais le caractère le plus remarquable du S.S.C. est son synchronisme mondial; il est plus ou moins ample en différents lieux, mais, partout où il est net, il apparaît au même instant en temps universel. À partir du début brusque, très généralement, l’agitation magnétique, marquée par des changements rapides et amples des valeurs des éléments magnétiques, est beaucoup plus grande qu’avant.

Après le début brusque, la composante horizontale, quoique agitée, conserve des valeurs supérieures à la normale pendant quelques heures: c’est la phase initiale ou positive de l’orage. Puis, l’agitation étant très forte, la composante horizontale prend des valeurs nettement inférieures à la normale, et cela pendant un temps qui est de l’ordre d’un jour. C’est alors que les écarts les plus grands sont observés, pouvant dépasser largement le degré pour D et le millier de gammas pour la composante H, en général nettement plus perturbée que la composante Z. Progressivement, le calme magnétique revient, mais la valeur de H reste inférieure à la normale, dont elle se rapproche peu à peu. C’est la «post-perturbation», dont la durée, mal définie, est de plusieurs jours. Aux latitudes élevées, ces phases successives ne sont pas observées, l’orage mondial correspond à une période d’agitation magnétique très intense.

Depuis plus d’un siècle, un nombre considérable de travaux ont été consacrés à l’explication de ce phénomène assez bien défini qu’est l’orage magnétique à début brusque. Le fait capital sur lequel s’appuie cette recherche est l’observation d’une liaison indiscutable entre orage et éruption chromosphérique solaire: l’orage suit une éruption forte avec un retard dont l’ordre de grandeur est la journée. Cela avait conduit à considérer qu’une large bouffée de plasma solaire (gaz très raréfié, entièrement ionisé, fait d’électrons et de protons) rencontrait subitement le champ magnétique terrestre, et le déformait, ce qui correspondait au S.S.C.; les forces de Laplace dues à l’action du champ terrestre sur les électrons et les protons déviaient leurs trajectoires, obligeant le flux de plasma à contourner la Terre; il s’établissait vers le plan de l’équateur géomagnétique un anneau de courant entourant la Terre, l’«anneau équatorial» par lequel on expliquait le fait que la phase principale correspondait à un champ quasi uniforme (et variable) agissant sur toute la Terre; la post-perturbation qui suivait correspondait à la disparition progressive des charges électriques dans l’anneau. Les idées nouvelles de vent solaire et de magnétosphère ont modifié les théories: l’orage serait dû à un renforcement brusque du vent solaire normal par l’arrivée de plasma émis par l’éruption; l’impact de la discontinuité sur la magnétosphère expliquerait le S.S.C.; et certains continuent à considérer qu’un ou deux anneaux de courant se formeraient à l’intérieur de la magnétosphère. Ce qui n’est pas clair encore, c’est la pénétration des charges dans cette magnétosphère. La théorie s’est élargie, avec Hannes Alfvén surtout, en devenant un problème de magnéto-hydrodynamique (en milieu très dilué), dans lequel on fait intervenir une propagation d’ondes hydromagnétiques ou «ondes d’Alfvén». Il est impossible de résumer les discussions, très difficiles, qui n’ont pas encore abouti à un ensemble cohérent. Ce qui paraît clair, c’est que les effets de l’orage mondial observés au sol proviennent d’événements dans la magnétosphère et non pas de courants dans l’ionosphère. Au contraire, les effets observés dans les régions aurorales seraient dus à de tels courants circulant en jet le long de la zone aurorale avec une plus forte intensité du côté nuit de la Terre; comme les aurores polaires, ils seraient provoqués par des arrivées d’électrons dans la haute atmosphère suivant un mécanisme qui reste inconnu, ces électrons étant maintenant considérés comme provenant de la «queue» de la magnétosphère. Ces événements, agitation magnétique et aurores, sont d’ailleurs bien plus fréquents que les orages observés partout sur le globe; ce sont des «orages polaires», phénomène journalier, dus à des renforcements inopinés du jet sur une partie plus ou moins étendue de la zone aurorale. Ils expliquent les particularités signalées antérieurement de la variation diurne S.

On observe fréquemment des périodes de forte agitation magnétique mondiale dont la durée est encore de l’ordre de la journée, mais dont le début n’est pas nettement marqué; on les appelle «orages à début progressif». Contrairement aux orages à début franc, ils ont une forte tendance à la récurrence de vingt-sept jours, et leur intensité maximale reste très inférieure à celle des orages à S.S.C. On les explique encore par un renforcement du vent solaire provenant, non pas d’un phénomène brusque comme l’éruption solaire, mais de cette émission continue, déjà signalée, de certaines régions solaires, venant balayer la Terre à chaque rotation du Soleil.

Parmi d’autres événements catalogués, citons le S.I. (sudden impulse ), sorte de S.S.C. non suivi d’un orage et de sens non privilégié, et la «baie magnétique». Les baies magnétiques correspondent à une déformation des courbes enregistrées, rappelant la forme d’une baie, dont la durée est de l’ordre de l’heure. C’est un phénomène fréquent, de nuit, aux latitudes moyennes; son ampleur croît quand on se rapproche de la zone aurorale où se déroule alors un orage polaire caractérisé par une très forte agitation irrégulière sur une partie de la zone. C’est en quelque sorte la conséquence lointaine de courants accidentels circulant sur la zone aurorale.

Variations rapides: pulsations

Beaucoup de chercheurs s’intéressent aux pulsations, et la masse des documents accumulés est considérable. Leur mise en ordre est difficile, et la théorie de l’origine de ces variations rapides l’est encore plus. Elle reste très incomplète jusqu’ici, d’autant plus que plusieurs mécanismes doivent jouer.

Assez vite, on avait déterminé toutes sortes de catégories dans les pulsations, dont la nomenclature était devenue compliquée et très variable suivant les auteurs. Actuellement, une classification, commode mais assez arbitraire, a été adoptée par tous. On y distingue deux familles: les pulsations régulières et continues, ou P^c , et les pulsations irrégulières, ou Pⁱ . Chaque famille est divisée en classes d’après la période du phénomène observé. Dans les P^c , on a fait cinq classes avec des indices de 1 à 5; par exemple, les périodes des P^c1 vont de 0,2 à 5 s, celles des P^c3 de 10 à 45 s, celles des P^c5 de 150 à 600 s. Les Pⁱ sont divisées en deux classes seulement.

Les Pⁱ semblent avoir leur origine dans des courants ionosphériques en relation avec les perturbations des régions aurorales. Parmi les pulsations régulières, les P^c1 ont d’abord été décrites comme «pulsations en perles»; elles correspondraient à un battement entre deux fréquences et, pour les vitesses courantes de déroulement, l’enregistrement ressemble à une succession de perles; les P^c3 , décrites depuis longtemps, sont remarquables par leur allure sinusoïdale assez régulière, leur présence très fréquente et continue, surtout durant le jour, les parentés qu’elles présentent sur de très grandes surfaces. Dans les deux cas, on cherche l’explication dans la propagation d’ondes d’Alfvén dans la magnétosphère.

Au-delà des pulsations de fréquence élevée encore étudiées avec des dispositifs purement magnétiques, on rejoint, avec un certain recouvrement, le domaine des oscillations naturelles étudiées par les radio-électriciens. Plusieurs naissent dans l’atmosphère à partir des éclairs; certaines n’ont pas de relation directe avec le champ magnétique terrestre (résonance de la cavité Terre-ionosphère et «atmosphériques»); d’autres, les «atmosphériques siffleurs», proviennent aussi d’une émission par les éclairs, mais avec propagation de l’énergie dans la magnétosphère et guidage par les lignes de force du champ magnétique terrestre.

• 1953; de géo- et magnétisme

Synonymes :

n. m. Didac. Magnétisme terrestre.

⇒GÉOMAGNÉTISME, subst. masc.

Magnétisme terrestre. La théorie du géomagnétisme. Cf. Hist. gén. sc., t. 3, vol. 2, 1964, p. 449.

Prononc. : []. Étymol. et Hist. 1953 (Lar. 20^e Suppl.). Dér. de magnétisme; élém. préf. géo-; cf. angl. geomagnetism, 1938 ds NED Suppl.

géomagnétisme [ʒeɔmaɲetism(ə)] n. m.

ÉTYM. Mil. XX^e (1953, Larousse); de géo-, et magnétisme.

❖

♦ Didact. Magnétisme terrestre.