Akademik

BRUIT DE FOND

En matière de transmission, on appelle bruit l’ensemble des signaux nuisibles qui se superposent au signal utile en un point quelconque d’une chaîne de mesure ou d’un système de transmission. Le signal utile représente l’information désirée alors que le bruit constitue une gêne dans la compréhension de l’information véhiculée par le signal.

1. Généralités sur le bruit

Bruit d’origine externe

On considère par exemple le cas d’un organe de transmission linéaire attaqué par un signal sinusoïdal V^e (t ) restituant en sortie un signal sinusoïdal V^s (t ) de même fréquence mais d’amplitude différente (fig. 1).

Si le câblage de cet organe est imparfait, un signal haute fréquence B(t ) émis par des systèmes environnants peut être capté par effet d’antenne et se superposer au signal utile V^s (t ), de sorte que le signal obtenu en sortie soit V ^s (t ).

Ce phénomène est bien connu des techniciens qui, en approchant la main du système de transmission, font disparaître la perturbation par effet de masse. Un blindage approprié permet dans ce cas d’éliminer le bruit d’origine externe B(t ).

Dans cette catégorie de bruits, on rencontre les bruits d’origine artificielle liés à l’activité humaine et les bruits d’origine naturelle:

– Les parasites industriels exercent principalement leur influence dans les villes. Leurs causes sont multiples: maniement des interrupteurs, moteurs électriques, enseignes lumineuses, allumage des automobiles...

– Les parasites atmosphériques sont provoqués par des orages, des décharges atmosphériques ou des échanges électriques entre nuages.

– Les parasites solaires et cosmiques d’origine extraterrestre peuvent être observés en pointant une antenne directionnelle vers le Soleil ou la Voie lactée. En pratique, ils ont peu d’influence sur les équipements électroniques utilisés en radiocommunications mais ils sont d’un grand intérêt dans l’étude des radiosources.

– Le bruit thermodynamique dû au rayonnement des corps est régi par la loi de Planck sur le «corps noir». Il est lié à des transitions radiatives dont les caractéristiques dépendent de l’agitation des électrons, c’est-à-dire de la température du corps.

Bruit d’origine interne

Si l’on considère maintenant un récepteur de radiodiffusion accordé sur une station émettrice suffisamment proche, on n’entend que le programme diffusé par la station et qui constitue ici le signal utile. Toutefois, pour peu que l’émetteur soit éloigné ou que le récepteur soit mal accordé, il est aisé de percevoir – superposé au signal vocal ou musical – un bruit confus, sorte de chuchotement, de souffle ou de ronflement communément appelé bruit de fond. Il s’agit cette fois d’un bruit interne à l’appareillage électronique qui se manifeste en présence ou non du signal utile.

2. Origines du bruit de fond

Le bruit de fond des équipements électroniques est lié aux fluctuations spontanées qui affectent une grandeur électrique (tension, courant ou champ) dans les divers composants actifs ou passifs des circuits. Ces fluctuations sont dues au caractère particulaire de l’électricité et en particulier au fait que les grandeurs précédentes dépendent de mouvements désordonnés de charges élémentaires. Ces charges sont généralement en très grand nombre et leur action globale nous apparaît comme constante ou continûment variable.

Toutefois, chaque particule étant animée d’un mouvement aléatoire, la grandeur électrique considérée fluctue également de manière aléatoire autour de sa valeur moyenne.

Ces fluctuations spontanées dans les composants sont des bruits d’origine interne qui constituent comme tels une limitation de base à la transmission d’une information sous forme électrique. Les deux sources principales de bruit d’origine interne sont:

– Le bruit thermique, ou bruit Johnson, qui apparaît dans les résistances au sens large du terme. Il est dû à l’agitation thermique des électrons dans les conducteurs et augmente donc avec la température.

– Le bruit de grenaille, ou bruit Schottky, qui apparaît dans les sources de courant électronique (diodes, transistors, tubes...). Il est dû à l’émission discrète des porteurs de charge qui s’accompagne inévitablement de fluctuations.

Dans un tube à plusieurs électrodes (triode ou pentode), vient s’ajouter un bruit dit de répartition (en anglais: partition noise ), qui provient du partage du courant entre les diverses électrodes. Ce dernier existe également dans les transistors, où il y a répartition du courant d’émetteur entre la base et le collecteur. Il existe d’autres types de bruit qui – contrairement au bruit thermique et au bruit de grenaille – dépendent de la fréquence. Le plus important d’entre eux est le bruit de scintillation (en anglais: flicker effect ) qui apparaît aussi bien dans les tubes que dans les transistors; il est à variation lente; c’est la raison pour laquelle il prédomine en basse fréquence, d’où son appellation de «bruit en 1/f ». On l’attribue à des inhomogénéités dans la réalisation des composants: très marqué dans les composants de technologie ancienne (tubes), il est plus faible pour les transistors à jonction et devient, dans la plupart des cas, négligeable pour les transistors à effet de champ (F.E.T.), qui ont subi moins d’opérations en cours de fabrication. Ce type de bruit se manifeste également dans les résistances au carbone et les résistances à couche mince.

Parmi les autres types de bruit importants en basse fréquence, citons pour les semi-conducteurs le bruit de génération-recombinaison et le bruit en créneaux (en anglais, burst noise ou popcorn noise ). Le bruit de génération-recombinaison est lié à des phénomènes de capture aléatoire sur des centres recombinants ainsi qu’à des phénomènes de régénération dans les bandes de conduction et de valence.

Le bruit en créneaux se caractérise par une instabilité du niveau moyen de signal qui effectue des transitions rapides d’un niveau à un autre; il a été mis en évidence dans les diodes tunnel, les diodes à jonction, les transistors bipolaires et les circuits intégrés.

3. «Protection» contre les bruits

«Protection» contre les bruits externes

Il est en général possible de protéger un montage contre les bruits d’origine externe grâce à un blindage approprié, mais, lorsqu’il s’agit d’une chaîne de réception, l’antenne est soumise de manière indissociable à l’information utile et au bruit capté. On doit alors traiter le signal brouillé en utilisant les méthodes de la théorie du signal (par exemple choix de la modulation, filtrage adapté...) ainsi qu’éventuellement les méthodes modernes de la détection (théorie de la décision).

La théorie de l’information apporte également une technique de protection originale. D’une manière générale, le bruit diminue l’intelligibilité d’une transmission: on dit qu’il amoindrit la quantité d’informations contenue dans le signal transmis. Ainsi une information surabondante (ou redondante) peut-elle avoir un effet compensateur, le moyen utilisé étant celui du codage, et l’on distingue en particulier les codes détecteurs d’erreur et les codes correcteurs d’erreur.

«Protection» contre les bruits internes

On ne peut se protéger totalement contre les bruits internes puisqu’ils trouvent leur origine dans les équipements électroniques eux-mêmes. On cherche alors à réaliser des dispositifs «le moins bruyants» possible. Pour ce faire, il est nécessaire, après avoir recensé les différentes sources de bruit interne, de connaître les lois qui les régissent et, avant tout, d’être en mesure de les caractériser.

4. Caractérisation du bruit de fond

Modélisation mathématique

Le modèle mathématique qui sert à traiter des problèmes de bruit est celui du processus aléatoire, pour l’étude rigoureuse duquel il convient de se reporter à la théorie des probabilités et des statistiques.

Les sources usuelles de bruit peuvent être représentées par des processus X(t ) stationnaires (leurs propriétés statistiques sont indépendantes d’une translation quelconque dans le temps) et ergodiques (leurs moyennes au sens des probabilités peuvent être remplacées par les moyennes temporelles correspondantes). L’espérance mathématique est alors égale à la moyenne temporelle:

et le moment d’ordre deux est égal à la moyenne temporelle du carré:

戀

連X²(t ) est appelée valeur quadratique moyenne. C’est une grandeur essentielle qui – à un facteur convenable près – représente la puissance moyenne du signal de bruit X(t ).

On sait par ailleurs que, pour les signaux déterministes, il existe un moyen simple de passer d’un signal temporel à ses caractéristiques fréquentielles en utilisant la transformée de Fourier. Cette transformation n’est pas directement utilisable dans le cas d’un signal aléatoire. Cependant, le théorème de Bochner-Wiener-Khintchine nous indique qu’il suffit de prendre alors la transformée de Fourier de la fonction d’autocorrélation du processus pour obtenir la densité spectrale de puissance:

avec:

Si X(t ) représente une tension, p (f ) s’exprime en V²/Hz.

La fonction d’autocorrélation traduit – pour un processus stationnaire ergodique – l’influence moyenne d’une valeur observée à un instant donné t 漣 淪 sur la valeur observée à un instant ultérieur t. On établit en particulier que la largeur utile de spectre d’un bruit est d’autant plus grande que la fonction d’autocorrélation décroît rapidement avec le retard 淪.

Exemple du bruit blanc: on appelle ainsi un bruit dont la densité spectrale de puissance est uniforme. En pratique, cette notion ne s’applique qu’à une bande finie f de fréquences: on parle dans ces conditions de bruit blanc à spectre borné.

Application au filtrage du bruit: on rappelle qu’un filtre est un système de convolution pour lequel l’action x (t ) et la réponse y (t ) sont liées par la relation:

où h (t ) représente la réponse impulsionnelle du filtre. On obtient la fonction de transfert H(f ) en appliquant la transformée de Fourier à h (t ):

et l’on montre que si le signal d’entrée est un bruit N^e (t ) de densité spectrale de puissance n ^e (f ), le signal de sortie N^s (t ) a pour densité spectrale:

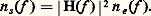
La puissance P^s du signal de sortie est donc égale à:

Si le bruit appliqué à l’entrée est un bruit blanc de densité unilatérale (fréquences positives) ⁰, la puissance de bruit en sortie vaut:

La quantité (1/(|H^max|²)) 咽⁺ size=1^秊0 |H(f )|² df définit la bande passante énergétique du filtre. Cette relation est fondamentale, elle permet de connaître la puissance de bruit en sortie du filtre attaqué par un bruit blanc en effectuant le simple produit:

À titre d’exemple, indiquons qu’on montre ainsi que la bande énergétique de bruit d’un circuit oscillant de bande passante F à 3 dB vaut 神/2 fois cette valeur: B = ( 神/2) F.

Le bruit de fond des résistances

Densité spectrale de puissance

Le bruit de fond des résistances – au sens large du terme – est un bruit d’origine thermique qui apparaît dans tout composant dont la caractéristique est à l’origine d’une dissipation d’énergie: résistance pure, résistance de perte d’un condensateur ou d’une bobine d’auto-induction, résistance de base d’un transistor à jonction, résistance de rayonnement d’une antenne... D’un point de vue théorique, la thermodynamique statistique permet d’établir que les électrons – par leur agitation thermique dans un conducteur à la température absolue T – constituent un générateur de bruit de densité spectrale unilatérale de puissance:

où f représente la fréquence en hertz (Hz); h = 6,62 練 10^-34 joule.seconde (J.s) est la constante de Planck, k = 1,38 練 10^-23 joule/kelvin (J/K) est la constante de Boltzmann.

Dans le domaine radioélectrique, hf 廉 k T, de sorte que n (f ) 年 k T. La densité spectrale de puissance est alors indépendante de la fréquence: le bruit thermique est, dans ces conditions, un bruit blanc (l’aspect quantique a disparu puisque la constante de Planck n’intervient plus).

Ainsi, à T = 293 K (20 ⁰C), la densité de puissance de bruit vaut 4,04 練 10^-21 W/Hz, soit 漣 204 dBW(10 log(k T/1 W), ou encore 漣 174 dBm (10 log (k T/1 mW).

Pour une bande de fréquence f , la puissance de bruit vaut k T f .

Ainsi pour f = 100 GHz, N = 400 pW.

Relation de Nyquist

On rappelle qu’un générateur de force électromotrice (f.e.m.) E^g et d’impédance interne Z^g fournit à une charge Z^c une puissance maximale (dite puissance disponible du générateur) lorsque Z^c est conjuguée de Z^g : Z^c = Z^g .

Dans le cas où Z^g = R^g , cette puissance disponible vaut (E^{g 2})/(4R^g ).

On détermine ainsi la force électromotrice de bruit dans une bande f sous forme quadratique moyenne en identifiant la puissance disponible de bruit k T f à l’expression générale de la puissance disponible:

On obtient alors l’égalité e ² = 4k TR f , connue sous le nom de relation de Nyquist. C’est en 1928 que Johnson a vérifié expérimentalement à mieux que 1 p. 100 cette formule; le bruit thermique est donc également appelé bruit Johnson.

Il est à remarquer que la valeur moyenne du bruit étant nulle, c’est à partir de la mesure de la tension quadratique moyenne que l’on détermine la force électromotrice efficace de bruit grâce au voltmètre efficace vrai (dit encore R.M.S. pour Root Mean Square): face=F0019 連e ² = 2 連k TR f .

Si l’on considère par exemple le cas d’un doublet demi-onde utilisé pour capter un émetteur terrestre, la température au sol étant de 20 ⁰C, la largeur de bande du récepteur f = 1 MHz, et la résistance de rayonnement du doublet voisine de 73 行, la force électromotrice de bruit aux bornes de cette antenne est de:

soit environ 1,1 猪V.

Représentation d’une résistance bruitée

On peut donner d’une résistance – considérée comme source de bruit – un schéma équivalent selon la représentation de Thévenin (ou de Norton) dont la force électromotrice (ou le courant électromoteur) produit la même puissance disponible (fig. 2):

Les sources équivalentes e et j ne sont pas polarisées et on les représente par les symboles usuels sans indication de polarité, l’intérieur étant grisé.

Pour donner un ordre de grandeur des tensions ou des courants de bruit, on obtient à T = 293 K et f = 1 MHz, pour R = 50 行, une tension efficace de bruit 連e ² = 0,90 猪V^eff, et un courant efficace de bruit 連j ² = 17,9 nA^eff.

Combinaison de plusieurs bruits

Lorsque deux bruits ne sont pas corrélés – c’est-à-dire que les fluctuations qui les engendrent sont indépendantes –, ils s’ajoutent quadratiquement. On établit alors que deux résistances en série R¹ et R² respectivement aux températures ¹ et ² sont équivalentes à une seule résistance R = R¹ + R² portée à la température:

De même, deux résistances en parallèle R¹(T¹) et R²(T²) sont équivalentes à une seule résistance R telle que 1/R = 1/R¹ + 1/R² portée à la température:

Bruit dans les dipôles passifs

La théorie montre que le bruit thermique ne prend sa source que dans les résistances et que les réactances (inductances et capacités) réalisées de manière parfaite (inexistence de perte ohmique) ne produisent aucun bruit. Ainsi dans un dipôle passif, seules les

résistances produisent du bruit, et la densité de puissance disponible, si le dipôle est à température uniforme T, est identique à celle d’une résistance pure: N = k T. On montre en fait que c’est la partie réelle de l’impédance du dipôle qui est source de bruit et qu’en toute généralité les densités de force électromotrice e ou de courant électromoteur j dépendent cette fois de la fréquence: e ² = 4k TR^e (Z(f )) et j ² = 4k TR^e (Y(f )).

Le bruit de grenaille

Il se manifeste essentiellement dans les composants électroniques où les porteurs de charge sont peu nombreux et circulent à des vitesses très grandes (tubes et semiconducteurs), au contraire des conducteurs où les électrons sont beaucoup plus nombreux et leur vitesse plus faible (quelques dixièmes de mm/s pour des densités de courant de plusieurs A/mm²) et pour lesquels le bruit de grenaille est négligeable devant le bruit d’origine thermique.

La diode à vide saturée

La tension d’anode est alors suffisante pour que tous les électrons émis par la cathode atteignent la plaque. Cette diode est équivalente à un générateur de courant I(t ) = I^s + i (t ), où I^s est le courant continu de saturation et i (t ) un courant aléatoire de valeur moyenne nulle et dont la valeur quadratique moyenne est donnée par la formule de Schottky (1918):

où q = 1,6 練 10^-19 coulomb est la charge de l’électron et f la bande d’analyse du système de mesures. Le bruit de grenaille est donc un bruit blanc, et cette approche constitue une très bonne approximation qui reste valable jusqu’à des fréquences très élevées (par exemple supérieures au gigahertz pour un tube de distance interélectrodes 3 mm avec une tension appliquée de 300 V).

La diode à jonction polarisée en direct

On obtient une relation de même forme que précédemment: I(t ) = I^d + i (t ), où I^d est le courant de conduction directe I^s exp(q V/k T) avec I^s , courant de saturation inverse et V^d , tension de polarisation directe. i (t ) admet comme valeur quadratique moyenne: i ² = 2q I^d f . En régime de petits signaux, la diode à jonction est équivalente au schéma de la figure 3, où r ^d représente la résistance différentielle (k T)/(q I^d ) et C^d la capacité de diffusion.

La densité de courant de bruit est donc i ² = 2q I^d = 2k T g ^d , avec g ^d = 1/r ^d ; la puissance de bruit disponible aux bornes d’une diode à jonction polarisée en direct est donc la moitié de celle que produirait une résistance métallique de valeur identique à la résistance différentielle de la diode. On obtient alors les schémas équivalents de la diode avec bruit donnés par la figure 4, avec e ² = 2k T r ^d , ou bien i ² = 2k T g ^d .

Les ordres de grandeur du courant de bruit à T = 293 K et pour f = 1 MHz sont:

et:

5. Le bruit de fond dans les systèmes de transmission

Après avoir étudié les sources principales de bruit des composants électroniques, il est désormais essentiel de caractériser les systèmes de transmission eux-mêmes. Pour ce faire, on utilise les résultats classiques de la théorie des circuits.

Facteur de bruit

Facteur de bruit ponctuel

Soit un quadripôle réel Q à la température de référence ⁰ = 293 K (température ambiante standard) attaqué par une source de résistance interne R^g à la même température ⁰ (fig. 5). On appelle alors G^d son gain en puissance disponible.

La puissance disponible de bruit N^e vaut k ⁰ df , où df désigne une bande de fréquences faible vis-à-vis de la bande passante du quadripôle, et pour laquelle les caractéristiques de celui-ci demeurent constantes. Si le quadripôle était parfait (bruit de fond nul), la puissance disponible de bruit en sortie serait :

Dans le cas réel, le quadripôle est bruyant et la puissance réelle de bruit en sortie vaut N^sr avec N^sr 礪 N^sp .

On appelle facteur de bruit le rapport F = N^sr /N^sp de la puissance réelle de bruit à la puissance inévitable de bruit en sortie du quadripôle. F est donc un nombre réel, sans dimension, supérieur à l’unité (F vaut 1 dans le cas d’un quadripôle parfait).

On l’exprime souvent en décibel à partir de la relation ^dB = 10 log F. Si l’on fait intervenir la puissance disponible de signal utile S^e du générateur d’attaque et la puissance disponible S^s du signal utile en sortie du quadripôle, on obtient une nouvelle expression du facteur de bruit:

Le facteur de bruit représente donc également la dégradation du rapport signal à bruit engendrée par le quadripôle de transmission à la température ⁰. De manière à fixer quelques ordres de grandeur, indiquons qu’une communication téléphonique physiologiquement parfaite implique un rapport signal à bruit d’environ 40 dB et qu’il en est sensiblement de même pour une image de télévision considérée comme excellente; par contre, au-dessous d’un rapport de 26 dB en télévision, l’image devient de qualité insuffisante alors qu’un rapport de 20 dB en téléphonie permet encore une compréhension correcte.

Quelques remarques importantes sont à faire à propos du facteur de bruit:

– Il caractérise l’ensemble quadripôle-résistance de source R^g : il dépend des conditions d’adaptation entre la source et l’entrée du quadripôle; par contre, il est indépendant des conditions de charge de ce dernier.

– Il se rapporte par définition à une source placée à la température de référence ⁰: ce point est important en métrologie du bruit.

– Il ne représente effectivement la dégradation du rapport S/N que si, premièrement, la source et le quadripôle sont à la même température ⁰, et, deuxièmement, si la puissance disponible de bruit N^e est uniquement due à R^g .

– La dégradation du rapport S/N dépend de la température de l’amplificateur, car le bruit qu’il produit en dépend donc N^sr aussi.

Facteur de bruit moyen

Si l’on considère une bande de fréquences f = f ² 漣 f ¹, on peut définir un facteur de bruit moyen par:

En général, dans le cas d’un amplificateur, F 漣 diffère assez peu de F(f ) dans sa bande passante.

Température équivalente de bruit

L’expression N^sr = F G^d k ⁰ df peut se mettre sous la forme:

où le premier terme représente la puissance inévitable de bruit N^sp et où le second terme ^Q caractérise la contribution propre du quadripôle au bruit réel mesuré à sa sortie.

On définit alors la température équivalente de bruit du quadripôle Q par la relation ^Q = (F 漣 1)⁰ qui permet d’exprimer le bruit propre ^Q sous la forme d’une élévation ^Q de température de la source de bruit de résistance interne R^g : N^Q = G^d k ^Q df .

Ainsi tout se passe comme si le quadripôle n’était pas bruyant, et la source portée à la température ⁰ + ^Q (fig. 6).

Il en est de même si la source est à une température quelconque T^s : la température de source et la température de bruit du quadripôle sont additives. Cette notion fournit, en particulier dans le cas des faibles bruits, un critère beaucoup plus sensible que celui du facteur de bruit, et c’est la raison pour laquelle elle remplace très souvent la traditionnelle notion de facteur de bruit.

Association de quadripôles

On considère n quadripôles placés en cascade (fig. 7) et on appelle Fⁱ le facteur de bruit et G^di le gain en puissance disponible de Qⁱ attaqué par l’impédance de sortie du quadripôle Q^i-1 .

La puissance disponible de bruit en sortie du premier quadripôle vaut:

où N^e est la puissance disponible de source k ⁰df . En sortie de Q²: N^{sr 2} = G^{d 2}N^{sr 1} + ^Q2, et en sortie de Qⁿ :

Dans le cas idéal où les différents quadripôles seraient tous non bruyants, on aurait N^{sp n} = G^{d 1}G^{d 2} ... G^{d n} N^e . Le facteur de bruit est par conséquent:

Utilisons la relation ^Qi = (Fⁱ 漣 1)G^{d i} N^e ; cette expression devient:

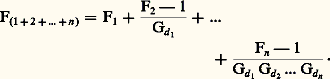
Cette relation fondamentale, connue sous le nom de formule des quadripôles en cascade ou formule de Friis, peut également s’écrire en fonction des températures de bruit grâce à l’équivalence ^Qi = (Fⁱ 漣 1)⁰:

où ^{Q(1+2+...+n )} représente la température équivalente de bruit à l’entrée de la chaîne. Il apparaît donc clairement que le facteur de bruit d’un réseau en cascade est essentiellement influencé par le premier étage et est d’autant plus réduit que son gain est important.

Température apparente de bruit

La notion de température équivalente de bruit se rapporte à l’entrée d’un quadripôle, mais l’on peut définir une autre notion dite température apparente de bruit, qui s’applique à toute source bruyante et qui la caractérise par rapport au bruit qu’elle délivre. Pour cela, il suffit d’identifier la densité de puissance de bruit fournie par la source à la densité de bruit thermique k T^a prise comme référence. Cette notion constitue une manière intéressante de caractériser les quadripôles qui ne sont pas des amplificateurs, telles les lignes de transmission ou les antennes. Dans ce dernier cas, on définit la température apparente d’antenne en identifiant la totalité du bruit qu’elle collecte dans une bande de fréquences df au bruit thermique k T^a df . Cela revient à considérer la résistance de rayonnement (ou plus exactement la résistance d’entrée de l’antenne) comme une source de bruit Johnson à la température T^a .

Calcul du facteur de bruit

Facteur de bruit d’un quadripôle passif

De la définition du facteur de bruit, on tire N^sr = FN^sp = FG^d k ⁰ df . Or la puissance de bruit d’un quadripôle passif à la température uniforme ⁰ vaut k ⁰ df . Le facteur de bruit cherché est donc égal à l’inverse du gain en puissance disponible G^d . Ce résultat très simple s’applique en particulier aux lignes de transmission.

Facteur de bruit d’un quadripôle actif

On montre que tout quadripôle réel peut être représenté par un quadripôle non bruyant associé à deux sources de bruit e ^{n 2} et j ^{n 2}, en général corrélées (fig. 8).

En appliquant la définition du facteur de bruit, on peut montrer que F est de la forme F = A + BR^g + C/R^g lorsque le quadripôle est attaqué par une source de résistance R^g avec A, B et C des constantes indépendantes de R^g . Le facteur de bruit admet donc un minimum pour une valeur optimale de la résistance d’attaque R^g :

Calcul de la température de bruit

Soit l’exemple d’une liaison spatiale pour laquelle le récepteur de température de bruit ^R est relié à l’antenne de température apparente T^a par l’intermédiaire d’une ligne d’affaiblissement A et de température vraie T.

Si l’on effectue les calculs pour la bande passante de l’ensemble du circuit de réception, la température équivalente de bruit de la chaîne de réception vue au niveau de l’antenne-source est égale, d’après la formule de Friis, à (A 漣 1) T (contribution de la ligne de transmission) + A^R (contribution du récepteur). D’où une température totale de bruit ^tot = T^a + (A 漣 1)T + A^R.

Réduction du bruit dans les systèmes de transmission

Pour diminuer la puissance de bruit dans un système de transmission, il est nécessaire de réduire sa température de bruit. Ainsi, dans l’exemple précédent, on utilise des antennes à faible température apparente (de type Cassegrain en particulier), une ligne à faible perte éventuellement refroidie et un récepteur à très faible bruit pour lequel on a également recours aux techniques cryogéniques. Dans le cas des récepteurs ultrasensibles pour communications par satellites, on refroidit les circuits d’entrée jusqu’à une température voisine de 4 K et l’on fait appel à des masers comme éléments d’amplification. Pour des réceptions moins critiques, on utilise des amplificateurs paramétriques refroidis (c’est le cas de nombreux récepteurs radars).

On a aussi intérêt à réduire au mieux la bande passante du récepteur en tenant compte des exigences du signal transmis. Dans un certain nombre de liaisons (radio ou télédiffusion, télémesures, téléphonie...), le signal à transmettre doit être adapté au canal de transmission par des méthodes de modulation dont les plus connues sont la modulation d’amplitude (AM) et la modulation de fréquence (FM). On montre alors que pour les mêmes conditions de rapport signal à bruit avant démodulation, une amélioration importante de ce rapport peut être obtenue en FM. Pour la radiodiffusion sonore, l’amélioration obtenue en FM par rapport à celle obtenue en AM (ou gain de modulation) est d’environ 19 dB au détriment d’une bande passante six fois plus large. En pratique, cet avantage n’est effectif que si le rapport S/N avant démodulation dépasse un certain seuil (de l’ordre de 6 à 10 dB).

En dessous de ce seuil, la dégradation du rapport S/N après démodulation est spectaculaire et on parle de capture du signal par le bruit. Dans le cas contraire, l’amélioration du rapport S/N après démodulation est très nette et on parle alors de capture du bruit par le signal; une illustration courante de ce phénomène en est faite lorsque l’on recherche l’accord d’un récepteur FM où le bruit de fond est important en phase de recherche et disparaît totalement lorsque l’accord est réalisé: la capture du bruit par le signal s’effectuant en fait grâce au signal porteur.

Application aux équipements de radioastronomie

À titre d’illustration, nous présenterons les caractéristiques et les performances d’équipements utilisés en radioastronomie. Les récepteurs utilisés à la station d’observation de Nançay dans le Cher fonctionnent, en ondes centimétriques, à 18 cm et 21 cm de longueur d’onde. Ils permettent l’étude de nuages moléculaires de notre Galaxie (formés en particulier d’ions OH^- et H⁺). L’équipement complet comporte une antenne mobile qui se présente sous la forme d’un miroir plan (de dimensions 35 m 憐 300 m) éclairant un miroir sphérique fixe qui concentre l’énergie reçue au niveau d’un cornet associé à un guide d’ondes. La température d’antenne T^a est de l’ordre de 30 K et les pertes A du guide d’ondes de 0,2 dB environ. L’étage d’entrée du récepteur est constitué d’un amplificateur à transistors à effet de champ dont le gain en puissance disponible G^{d 1} vaut 30 dB. Cet étage ainsi que le guide d’ondes associé sont placés dans une enceinte refroidie à une température vraie T = 20 K grâce à un système réfrigérant de type hélium gazeux: sa température équivalente de bruit ¹ est alors de 10 K (si le système n’est pas refroidi mais simplement régulé à T = 300 K, la température de bruit monte à 50 K). Le second étage non refroidi est à transistors bipolaires; il possède un gain d’environ 25 dB pour une température de bruit ² qui varie de 350 K à 650 K selon le modèle.

D’après les résultats des calculs effectués au début du chapitre Calcul de la température de bruit , la température totale au niveau de l’antenne vaut:

avec ¹ = 10 K et ² = 500 K; on trouve ^tot 年 42 K. Si l’on utilise un récepteur non refroidi, ^tot 年 97 K.

En ce qui concerne les récepteurs pour ondes millimétriques, tels ceux de l’observatoire de Bordeaux, ils sont utilisés pour la détection des molécules dans les nuages interstellaires vers 100 GHz. Le bruit du ciel lié aux problèmes de transparence dus à la vapeur d’eau est plus élevé qu’en ondes centimétriques: la température d’antenne et de ciel est comprise entre 50 K et 300 K. À Bordeaux, la moyenne est d’environ 80 K. L’équipement complet comporte cette fois une antenne parabolique de diamètre 2,5 m qui éclaire une lentille de focalisation (de perte A¹: 0,1 dB à ¹ = 300 K) illuminant le cornet associé au guide d’ondes (de perte A²: 0,3 dB à ² = 20 K).

L’étage d’entrée refroidi à 20 K comprend un mélangeur de perte A^m : 4 dB (en double bande) et de température de bruit T^m = 100 K qui est suivi de deux amplificateurs à transistors à effet de champ de 13 dB de gain chacun et de températures de bruit respectives ¹ = 15 K et ² = 20 K. Le second étage non refroidi est à transistors bipolaires; il possède un gain d’environ 25 dB pour une température de bruit de 250 K.

La température de bruit du système est donc égale à:

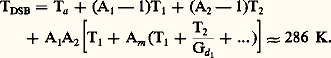
De manière à réduire la température d’antenne et de ciel, un système de réception de même type fonctionne à Dévoluy (observatoire de haute montagne situé dans les Alpes à 2 600 m d’altitude) sur une fréquence de 250 GHz (longueur d’onde de l’ordre du mm) où les pertes et le bruit atmosphériques sont plus faibles.