- ЗОННАЯ ТЕОРИЯ
-
твёрдых тел, квантовая теория энергетич. спектра эл-нов в кристалле, согласно к-рой этот спектр состоит из чередующихся зон (полос) разрешённых и запрещённых энергий. З. т. объясняет ряд св-в и явлений в кристалле, в частности разл. хар-р электропроводности тв. тел. Основы З. т. созданы нем. физиком Ф. Блохом (1928) и франц. физиком Л. Бриллюэном (1930).В основе З. т. лежит т. н. о д н о э л е к т р о н н о е п р и б л и ж е н и е, базирующееся на след. упрощениях:1) ат. ядра в узлах идеальной крист. решётки неподвижны (их масса велика по сравнению с массой эл-нов).2) Эл-н движется в поле периодич. потенциала U(r) (r — пространств. координата точки), к-рое складывается из полей, создаваемых ядрами и остальными эл-нами.3) Это периодич. поле обладает трансляц. инвариантностью:U(r+an)=U(r), (1)где аn — вектор n-го узла решетки.В такой модели для волн. ф-ции y эл-на в решётке выполняется теорема Блоха:yk(r)=uk(r)expkr, (2)где uk(r+a)=uk(r), k — волновой вектор эл-на.Это означает, что yk(r) имеет вид волн. ф-ции свободного эл-на, амплитуда к-рой промодулирована в пр-ве с периодом решётки.Спектр энергии 8 эл-нов можно определить, подставляя волн. ф-цию в виде (2) в стационарное Шредингера уравнение и вводя те или иные граничные условия. Решение ур-ния даёт энергетич. спектр в виде серии полос разрешённых энергий ?l(k) (l — номера разрешённых зон), разделённых полосами запрещённых энергий. Из (1) следует, что ?l(k+b)=?l(k), где b — вектор обратной решётки. Следовательно, ?l(k) — периодич. ф-ция с периодом b. Физически разл. значения k заключены внутри первой Бриллюэна зоны.В соответствии с З. т. движение эл-на в решётке сходно с движением эл-на в свободном пр-ве, однако фактически носит туннельный хар-р. Квазиимпульс эл-на в ре-щётке p=hk отличен от импульса свободного эл-на. Для него выполняются законы сохранения, справедливо ур-ние движения dp!dt=F (F — внеш. сила). Эл-н в кристалле оказывается квазичастицей с эффективной массой m*, отличной от массы свободного эл-на m0. Энергия эл-на явл. ф-цией квазиимпульса ?(р).Энергетич. структура каждой зоны описывается ф-цией ?(р), наз. дисперсии законом. Есть два осн. способа описывать энергетич. структуру зоны: 1) пусть координаты рх, ру и рz фиксированы, тогда ?(рx) — кривая на плоскости (?, рх) (дисперсионная кривая, рис. 1). Повторяя эту операцию для (?ру) и (?рг) получим набор дисперс. кривых, полностью характеризующих ф-цию ?(p). 2) Можно фиксировать какое-то значение энергии в к.-л. зоне ?l(p)=const. Это ур-ние поверхности в трёхмерном р-пространстве (изоэнергетич. поверхность). Изменяя константу, получим семейство изоэнергетич. поверхностей, характеризующих закон дисперсии. Изоэнергетич. поверхности обладают симметрией, связанной с симметрией кристаллов.Физически происхождение зонной структуры энергетич. спектра эл-нов в кристалле связано с образованием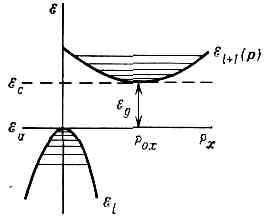 Рис. 1. Дисперсионные кривые ?l(рх) и ?l-1(px) при фиксированных pу и pz: ?с — дно l+1-й зоны (зоны проводимости), ?v — потолок l-той зоны (валентной зоны); ?g — ширина запрещённой зоны; заштрихованные области — уровни, заполненные эл-нами и дырками.кристалла из N атомов, каждый из к-рых в свободном состоянии обладает дискретным электронным энергетич. спектром. При объединении N атомов в кристалл последний можно трактовать как гигантскую молекулу, в к-рой эл-ны всех атомов обобществлены и к-рую следует рассматривать как единую квантовомеханич. систему. В кристалле каждый из ат. уровней превращается в полосу, состоящую из N уровней (или с учётом спина — из 2N уровней), к-рая явл. разрешённой зоной ?l(p). Если на атом приходится Z эл-нов, то полное число эл-нов в кристалле равно NZ; они занимают уровни разрешённых зон начиная снизу, пока не будут полностью исчерпаны. Изоэнергетич. поверхность, соответствующая Ферми энергии: ?(p)=?F, наз. Ферми поверхностью. Ниж. зоны (довольно узкие) будут целиком заполнены эл-нами внутр. оболочек атомов. Заполнение эл-нами разрешённых энергетич. уровней происходит в соответствии с Ферми — Дирака распределением.Хотя структура энергетич. зоны дискретна, уровни весьма близки (квазинепрерывны). Для описания распределения энергетич. уровней в зоне n(?) часто вводят ф-цию плотности состояний (уровней) g(?)=dn/d? — число уровней на единичный энергетич. интервал. Вид ф-ции g(?) зависит от закона дисперсии. В простейшем случае, когда?(р)=р2/2m*, то g(?)=A?1/2, где А=(1/4p2) (2m*/h2)3/2.Физ. св-ва кристаллов определяются в осн. верхними зонами, ещё содержащими эл-ны. Эиергетич. интервал ?g между «дном» ?c (минимумом энергии) самой верхней ещё содержащей эл-ны зоны и «потолком» ?v (максимумом энергии) предыдущей целиком заполненной зоны, наз. запрещённой зоной (хотя ниже по энергии может быть ещё неск. др. запрещённых и разрешённых зон). Если при T=0 все зоны, содержащие эл-ны, заполнены эл-нами целиком, а следующая «пустая» разрешённая зона отделена от данной достаточно широкой запрещённой зоной, то кристалл явл. диэлектриком (напр., у алмаза ?g=5 эВ); если ?g?3 эВ, то — полупроводником. Если верхняя содержащая эл-ны зона заполнена эл-нами частично, то это металл. Возможно частичное перекрытие разрешённых зон или смыкание их (полуметаллы, бесщелевые полупроводники).Внеш. воздействия (повышение темп-ры, облучение, напр. светом, или сильные внеш. электрич. поля) могут вызвать переброс эл-нов через запрещённую зону. В результате появляются «свободные» носители заряда (эл-ны проводимости и дырки), осуществляющие проводимость.В ПП изоэнергетич. поверхность в зоне проводимости в простейшем случае явл. сферой или эллипсоидом. В более сложных случаях изоэнергетич. поверхность может быть многосвязной, напр. в виде совокупности эллипсоидов, «нанизанных» своими длинными осями на оси симметрии изоэнергетич. поверхности (рис. 2); для Ge их 8, для Si — 6. В этом случае в зоне проводимости есть неск. эквивалентных минимумов энергии. Области энергии в зоне проводимости вблизи каждого из минимумов наз. долинами, а ПП с неск. эквивалентными минимумами — многодолинными. В условиях равновесия эл-ны распределяются между долинами поровну.
Рис. 1. Дисперсионные кривые ?l(рх) и ?l-1(px) при фиксированных pу и pz: ?с — дно l+1-й зоны (зоны проводимости), ?v — потолок l-той зоны (валентной зоны); ?g — ширина запрещённой зоны; заштрихованные области — уровни, заполненные эл-нами и дырками.кристалла из N атомов, каждый из к-рых в свободном состоянии обладает дискретным электронным энергетич. спектром. При объединении N атомов в кристалл последний можно трактовать как гигантскую молекулу, в к-рой эл-ны всех атомов обобществлены и к-рую следует рассматривать как единую квантовомеханич. систему. В кристалле каждый из ат. уровней превращается в полосу, состоящую из N уровней (или с учётом спина — из 2N уровней), к-рая явл. разрешённой зоной ?l(p). Если на атом приходится Z эл-нов, то полное число эл-нов в кристалле равно NZ; они занимают уровни разрешённых зон начиная снизу, пока не будут полностью исчерпаны. Изоэнергетич. поверхность, соответствующая Ферми энергии: ?(p)=?F, наз. Ферми поверхностью. Ниж. зоны (довольно узкие) будут целиком заполнены эл-нами внутр. оболочек атомов. Заполнение эл-нами разрешённых энергетич. уровней происходит в соответствии с Ферми — Дирака распределением.Хотя структура энергетич. зоны дискретна, уровни весьма близки (квазинепрерывны). Для описания распределения энергетич. уровней в зоне n(?) часто вводят ф-цию плотности состояний (уровней) g(?)=dn/d? — число уровней на единичный энергетич. интервал. Вид ф-ции g(?) зависит от закона дисперсии. В простейшем случае, когда?(р)=р2/2m*, то g(?)=A?1/2, где А=(1/4p2) (2m*/h2)3/2.Физ. св-ва кристаллов определяются в осн. верхними зонами, ещё содержащими эл-ны. Эиергетич. интервал ?g между «дном» ?c (минимумом энергии) самой верхней ещё содержащей эл-ны зоны и «потолком» ?v (максимумом энергии) предыдущей целиком заполненной зоны, наз. запрещённой зоной (хотя ниже по энергии может быть ещё неск. др. запрещённых и разрешённых зон). Если при T=0 все зоны, содержащие эл-ны, заполнены эл-нами целиком, а следующая «пустая» разрешённая зона отделена от данной достаточно широкой запрещённой зоной, то кристалл явл. диэлектриком (напр., у алмаза ?g=5 эВ); если ?g?3 эВ, то — полупроводником. Если верхняя содержащая эл-ны зона заполнена эл-нами частично, то это металл. Возможно частичное перекрытие разрешённых зон или смыкание их (полуметаллы, бесщелевые полупроводники).Внеш. воздействия (повышение темп-ры, облучение, напр. светом, или сильные внеш. электрич. поля) могут вызвать переброс эл-нов через запрещённую зону. В результате появляются «свободные» носители заряда (эл-ны проводимости и дырки), осуществляющие проводимость.В ПП изоэнергетич. поверхность в зоне проводимости в простейшем случае явл. сферой или эллипсоидом. В более сложных случаях изоэнергетич. поверхность может быть многосвязной, напр. в виде совокупности эллипсоидов, «нанизанных» своими длинными осями на оси симметрии изоэнергетич. поверхности (рис. 2); для Ge их 8, для Si — 6. В этом случае в зоне проводимости есть неск. эквивалентных минимумов энергии. Области энергии в зоне проводимости вблизи каждого из минимумов наз. долинами, а ПП с неск. эквивалентными минимумами — многодолинными. В условиях равновесия эл-ны распределяются между долинами поровну.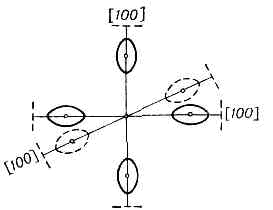 Рис. 2. Эллипсоиды пост. энергии в Si.При включении в данном направлении внеш. электрич. поля долины проявляют себя неэквивалентно из-за различий в величине эфф. масс и подвижностей эл-нов в разл. направлениях. Аналогичные эффекты имеют место и при воздействии одностороннего давления. Следствием этой неэквивалентности может быть, в частности, анизотропия электропроводности, оптич. св-в и т. п.Локальные нарушения идеальности решётки (примесные атомы, вакансии и др. дефекты) могут вызвать образование разрешённых локальных уровней и локальных зон внутри запрещённых зон. Применение З. т. возможно и в этом случае, и даже в случае аморфных тв. тел, хотя требует нек-рых модификаций (см. НЕУПОРЯДОЧЕННЫЕ СИСТЕМЫ).
Рис. 2. Эллипсоиды пост. энергии в Si.При включении в данном направлении внеш. электрич. поля долины проявляют себя неэквивалентно из-за различий в величине эфф. масс и подвижностей эл-нов в разл. направлениях. Аналогичные эффекты имеют место и при воздействии одностороннего давления. Следствием этой неэквивалентности может быть, в частности, анизотропия электропроводности, оптич. св-в и т. п.Локальные нарушения идеальности решётки (примесные атомы, вакансии и др. дефекты) могут вызвать образование разрешённых локальных уровней и локальных зон внутри запрещённых зон. Применение З. т. возможно и в этом случае, и даже в случае аморфных тв. тел, хотя требует нек-рых модификаций (см. НЕУПОРЯДОЧЕННЫЕ СИСТЕМЫ).
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- ЗОННАЯ ТЕОРИЯ
-
- один из осн. разделов квантовой теории твёрдых тел.3. т. описывает движение электронов в кристаллах и является основой совр. теории металлов, полупроводников и диэлектриков[1-4].
Электронные зоны в идеальном кристалле. Из-за близкого расположения атомов в кристаллах происходит перекрытие волновых ф-ций электронов соседних атомов или молекул. В результате из каждого дискретного энергетич. уровня атома или молекулы образуется энергетич. зона и электроны, находящиеся на этих уровнях, приобретают способность свободно перемещаться по кристаллу. Особенность кристалла, отличающая его от аморфных тел и жидкостей, - периодичность в расположении атомов, т. е. наличие трансляц. симметрии. Из-за трансляц. симметрии волновая ф-ция электрона в кристалле y(r) в точках с пространств, координатами r и r+а (а - вектор решётки) отличается лишь фазовым множителем:yk(r) = uk(r)exp(ikr), (1)
где uk(r+а)=uk(r). Здесь k - волновой вектор электрона (см. Блоха теорема, Елоховские электроны). Квазиимпульс
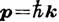 электрона является аналогом импульса свободного электрона, а величина l=2p/k - аналог длины волны де Бройля. Энергия электрона E(k) - периодич. ф-ция в k -пространстве:
электрона является аналогом импульса свободного электрона, а величина l=2p/k - аналог длины волны де Бройля. Энергия электрона E(k) - периодич. ф-ция в k -пространстве:E(k + g) =E(k), (2)
где g - любой из целочисленных векторов обратной решётки, построенной на базисных векторах g1, g2, g3, связанных с векторами прямой решётки а i соотношениями: g1=2p[a2a3]/Wи т. д. Здесь W=a1[a2a3] - объём элементарной ячейки кристалла. В качестве элементарной ячейки обратной решётки выбирают первую Бриллюэна зону (ЗБ). Объём ЗБ равен g1[g2g3]=(2p)3/W, а число электронных состояний в ЗБ (без учёта вырождения по спину) равно числу элементарных ячеек в объёме кристалла V, т. е. V/W. Т. о., плотность состояний в k-пространстве не зависит от k; и равна:
r(k) = V/(2p)3 (3)
Состояние электрона в кристалле ymk/(r) с энергией Em(k)характеризуется непрерывным квантовым числом k и номером энергетич. зоны или номером ветви m, спектра, если зона включает неск. ветвей. Предполагается, что k лежит в пределах первой ЗБ (схема приведённых зон, рис. 1, а). Генетически каждая из ветвей mсвязана с определ. уровнем атомов, составляющих кристалл. Число ветвей, образующихся из каждого атомного уровня, равно произведениюстепени вырождения этого уровня на число эквивалентных атомов в элементарной ячейке, т. е. атомов, меняющихся местами при преобразованиях симметрии, входящих в группу симметрии кристалла. В k-пространстве существуют точки, в к-рых неск. сocтояний ymk(r) с определ. k имеют одну и ту же энергию, т.e. соответствующие ветви спектра касаются или пересекаются.
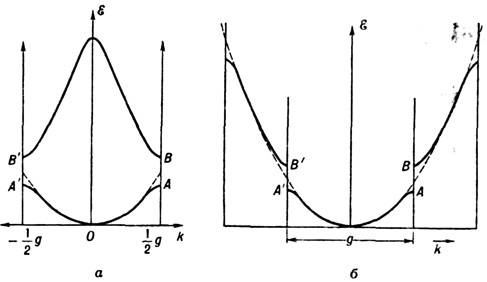
Рис. 1. Спектр электрона E(k) в приближении слабой связи (2 ветви): a - схема приведенных зон; б - схема расширенныхзон.Существование и положение этих точек (вырожденные точки), как правило, обусловлено пространств, группой симметрии кристалла, а также требованиями, накладываемыми условием инвариантности к инверсии времени. Такое вырождение может возникать не только в изолированных точках ЗБ, но и на осях симметрии и её гранях. Пример вырождения, связанного с инвариантностью к инверсии времени, - двукратное спиновое вырождение, к-рое в кристаллах с центром инверсии имеет место во всех точках ЗБ. Т. к. инверсия времени К обращает и направление k, и направление спина электрона, а пространств. инверсия I, обращая направление k, не влияет на спин, то в таких кристаллах ф-ции yk и KIyk, отвечающие одному и тому же значению Eи k, соответствуют разным спиновым состояниям. В кристаллах без центра инверсии спиновое вырождение может иметь место лишь в отд. точках, на осях симметрии и гранях ЗБ, для к-рых либо k=-k+g, либо имеется операция симметрии, обращающая k в -k+g. В остальных точках ЗБ инвариантность к инверсии времени требует лишь выполнения общего условия E(k)=E(-k)[5].Наряду с вырождением, обусловленным условиями симметрии, пересечение ветвей спектра в изолированных точках может быть и случайным. При наличии точек вырождения одному и тому же интервалу энергий могут соответствовать неск. ветвей спектра (т. н. вырожденная зона). Как правило, вырожденные зоны возникают из вырожденных состояний изолированного атома. Наряду с этим в кристалле могут перекрываться и ветви, произошедшие из разных атомных уровней. Такое перекрытие может не сопровождаться возникновением точек вырождения. Интервалы энергий, в к-рые попадают одна или неск. ветвей спектра, наз. разрешёнными зона-м и, интервалы, в к-рые ни одна из ветвей не попадает, - запрещёнными зонами. Иногда каждой из ветвей спектра Em(k), соответствующих разным разрешённым зонам, сопоставляют свою m-ю ЗБ, рассматривая спектр электронов во всём k-пространстве. Такая схема, наз. схемой расширенных зон (рис. 1, б), удобна при описании почти свободных электронов, т. к. при этом сохраняется соответствие между волновым вектором электрона в кристалле и волновым вектором свободного электрона. Поскольку свойство периодичности энергетич. спектра в k -пространстве - следствие только трансляц. симметрии, то (2) справедливо и для всех др. элементарныхвозбуждений, способных перемещаться по кристаллу и соответственно, как и электроны, обладающих квазиимпульсом (см. Квазичастица). Заполнение зон в идеальном кристалле. Число мест в одной зоне ограничено и равно для каждой ветви (невырожденной по спину) V/W. В силу Паули принципа каждое из этих состояний может быть заполнено только одним электроном. При темп-ре T=0К электроны заполняют ниж. состояния. В зависимости от числа валентных электронов верхняя из заполненных зон может быть занята полностью или частично. Электроны полностью заполненной зоны не переносят ток, т. к. в такой зоне электрич. поле не может изменить распределение электронов по квазиимпульсам. Поэтому кристаллы, у к-рых ниж. зоны полностью заполнены, а верхние пустые, являются диэлектриками или полупроводниками. Верхняя из заполненных зон таких кристаллов наз. валентной зоной, а нижняя из пустых - зоной проводимости (рис. 2, а).
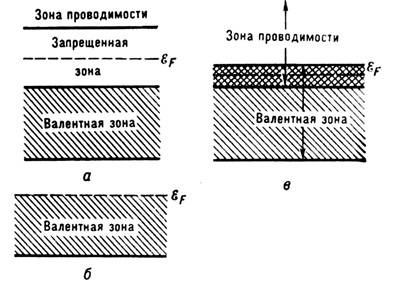
Рис. 2. Схема заполнения зон в диэлектриках и полупроводниках (а), металлах (б) и полуметаллах (в); EF - уровень Ферми.Вещества с широкой запрещённой зоной, разделяющей валентную зону и зону проводимости, являются диэлектриками, а вещества с более узкой запрещённой зоной (обычно меньше 2,5-3 эВ) - полупроводниками. Однако деление между ними в значит. мере условно. При частичном заполнении зоны внеш. электрич. поле может изменять распределение электронов по квазиимпульсам, так что возникает результирующий поток электронов создающий ток. Поэтому кристаллы с частично заполненными зонами являются металлами (рис. 2, б). Как правило, это кристаллы, образованные атомами с не полностью заполненными электронными оболочками. Кристаллы, составленные из атомов или ионов с полностью заполненными оболочками, - обычно диэлектрики или полупроводники. Напр., кристаллы инертных газов и щёлочно-галлоидные кристаллы типа NaCl, у к-рых все S-электроны катиона переходят на Р-оболочку аниона, полностью заполняя её, обычно - диэлектрики. Однако многие из таких кристаллов в результате перекрытия зон, соответствующих разным атомным уровням, становятся металлами, пример - щёлочно-земельные металлы. И наоборот, в результате расщепления атомных уровней внутрикристаллическим полем кристаллы, образованные атомами с не полностью заполненными оболочками, могут быть диэлектриками. Так, в одноосных кристаллах Р-уровень расщепляется на 2 подуровня, образующих 2 зоны, нижняя из к-рых м. б. полностью заполнена. Подобную роль может играть и ферромагнитное или антиферромагнитное упорядочение, снимающее вырождение по спину. Диэлектриками могут быть и кристаллы, содержащие в элементарной ячейке неск. атомов с не полностью заполненными оболочками. Пример - элементарные полупроводники IV группы периодич. системы (алмаз, Ge, Si), у к-рых элементарная ячейка содержит 2 атома, и VI группы (Se, Те) с 3 атомами в ячейке. Так, в алмазе, Ge, Si на 8 атомных S- и Р- уровнях (с учётом спина) приходится 4 электрона, т. е. эти уровни заполнены наполовину. Из этих 8 уровнейобразуются 4 зоны, две из к-рих трёхкратно вырождены. Из них 2 нижние полностью заполнены имеющимися 8 электронами в каждой ячейке. Остальные 2 зоны остаются пустыми и образуют зоны проводимости. При этом в верх. валентной зоне Ge (Г'25, рис. 3, а, 6), также как и в более высокой из зон проводимости (Г 15), в точке Г (центр ЗБ) имеет место трёхкратное вырождение, а на осях D и L - двукратное вырождение одной из ветвей (D, L3). Спин-орбитальное взаимодействие частично снимает это вырождение, расщепляя валентную зону в точке Г и по направлениям D и L [5, 10]. В ряде кристаллов частично заполненные зоны образуются в результате слабого перекрытия верх. заполненной зоны с нижней пустой. Такие вещества (графит, Bi, Sb) наз. полуметаллами (рис. 2, в).
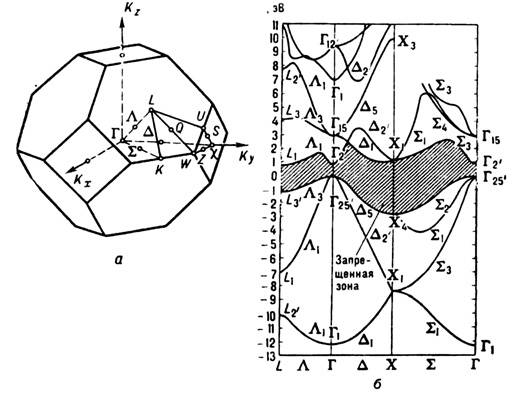
Рис. 3. а - Первая зона Бриллюэна Ge, Г - центр зоны Бриллюэна (k - 0), X, L, К и др.- "точки симметрии", переходящие сами в себя при преобразованиях симметрии, допустимых в данной решётке; б - Спектр электронов проводимости и дырок в Ge (без учёта спин-орбитального расщепления) в направлениях [111] (L), [100] (D), 110 (S) (индекс указывает номер неприводимого представления группы волнового вектора k); заштрихована запрещённая зона.В нек-рых полупроводниках (напр., серое олово) одна из ветвей, выходящих из точки вырождения (k0=0), идёт вверх, т. е. для неё E(k)>E(k0), а вторая вниз: E(k)<E(k0). При этом верх, ветвь пустая, а нижняя полностью заполнена, т. е. зона проводимости и валентная зона касаются в точке k0. Такие кристаллы наз. бесщелевыми полупроводниками. При T = 0K уровень Ферми EF определяет границу между заполненными и незаполненными уровнями (см. Ферми-энергия). В чистых полупроводниках и диэлектриках EF проходит в запрещённой зоне, разделяющей валентную зону и зону проводимости; в металлах или сильно легированных полупроводниках - в разрешённой зоне. В этом случае изоэнергетич. поверхность в k-пространстве, определяемая ур-нием Em(k)=EF, наз. поверхностью Ферми. Для пересекающихся или вырожденных зон её форма различная для каждой из ветвей спектра. В металле она может либо охватывать замкнутую область k-пространства, либо проходить через всю обратную решётку (см. Ферми-поверхность). При T>0К степень заполнения электронами состояния с энергией S определяется ферми-распределением:
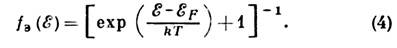
Положение уровня Ферми EF находится из ур-ния: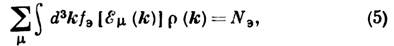
где N Э - полное число электронов в кристалле, задаваемое условием нейтральности, т. е. равенством полного заряда электронов заряду положит. ионов. Электроны и дырки, примесные уровни. При повышении темп-ры в полупроводниках и диэлектриках в соответствии с (4), (5) электроны начинают переходить из валентной зоны в зону проводимости, образуя пустые места в валентной зоне, наз. дырками. Движение носителей заряда в валентной зоне обычно описывают как движение дырок. Каждой дырке приписывают заряд и волновой вектор, равные с обратным знаком заряду и волновому вектору отсутствующего электрона. Энергия дырки E Д(k) = -E Э (-k) =-E Э(k), и вероятность заполнения дырочных состояний определяется ф-цией Ферми дырок: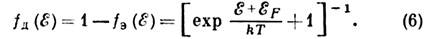
В полуметаллах движение носителей в нижней из перекрывающихся зон также описывают как движение дырок. В металлах с замкнутыми поверхностями Ферми последние могут ограничивать либо область энергий с E(k)[EF, либо область с E(k)>EF. В последнем случае движение носителей заряда описывается как движение дырок с E д(k)<-EF. Число пустых мест, ограниченных этой поверхностью, наз. числом дырок, тогда как в первом случае число электронов в области, где E Э(k)<EF, наз. числом электронов проводимости. Практически во всех металлах с замкнутыми поверхностями Ферми (кроме щелочных металлов) есть и электроны и дырки. Во всех кристаллах имеются уровни, связанные с дефектами кристаллич. решётки и чужеродными атомами. Заполнение уровней примеси также определяется (4). В металлах, имеющих большое число свободных электронов, переходы носителей с примеси в зоны не играют заметной роли. В полупроводниках и диэлектриках (а также в полуметаллах с большой концентрацией примеси) концентрация носителей при не очень высоких темп-pax определяется числом электронов, перешедших с донорных уровней в зону проводимости, или числом электронов валентной зоны, захваченных акцепторами с образованием дырок [9, 10].Наряду с объёмными уровнями в кристалле имеются поверхностные состояния. Волновая ф-ция электронов в этих состояниях локализована вблизи поверхности кристалла, внутри него. Различают собственные поверхностные состояния (уровни Тамма) и примесные. Уровни Тамма возникают в результате "обрыва" решётки на границе и искажения приноверхностных ячеек. Эти уровни образуют поверхностные зоны. Примесные поверхностные уровни связаны с дефектами и чужеродными атомами на поверхности. Обычно энергия электрона на дне зоны проводимости меньше его энергии в вакууме, однако в исключит. случаях - напр., в кристаллич. и жидком гелии (см. Гелий твёрдый) - дно зоны проводимости лежит выше уровня покоящегося электрона в вакууме и поэтому электроны из вакуума не могут проникать в кристалл; однако они, поляризуя кристалл, притягиваются к нему индуцированным на поверхности зарядом. В результате образуются поверхностные состояния с волновой ф-цией, локализированной вне кристалла у его поверхности. Основные методы расчёта зон. В первых расчётах зонной структуры использовались приближения слабой и сильной связи. В методе слабой связи в качестве нулевого приближения берутся волновые ф-ции свободного электрона (плоские волны), а периодич. поле кристалла рассматривается как возмущение. В этой модели электронный спектр E(k )почти во всём k-пространстве описывается той же ф-лой, что и для свободного электрона:
где m0 - масса свободного электрона, и лишь у границы зоны Бриллюэна испытывает разрывы (рис. 1, б). Эти разрывы связаны с брэгговским отражением электронов в кристалле; волновые векторы, для к-рых выполняется условие брэгговского отражения (см. Брэгга - Вульфа условие), как раз образуют поверхности зоны Бриллюэна. При этом каждая из граней зоны соответствует отражению от системы опрeдел. плоскостей прямой решётки. В отличие от состояний внутри ЗБ, к-рым соответствуют бегущие волны (1), всем состоянием на её поверхности соответствуют стоячие волны. Приближение слабой связи хорошо описывает электронный спектр простых металлов. Для определения формы их поверхности Ферми достаточно провести вокруг узла обратной решётки сферу, определённую условием k3F = 3p2N/V, где kF - фермиевский импульс, N - число валентных электронов (метод Xаррисона [7]). Если эта сфера выходит за пределы ЗБ, то форма поверхности Ферми оказывается несферической. Если возмущающий потенциал не мал, то волновую ф-цию (1) можно разложить по векторам обратной решётки g:yk(r) = exp (ikr)SgGgexp(igr), (8)
и задача сводится к решению секулярного ур-ния:
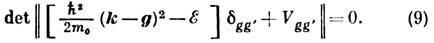
Т. к. волновая ф-ция валентных электронов ортогональна Волковым ф-циям нижележащих состояний, она сильно осциллирует вблизи атомных остовов. Поэтому вклад в энергию валентных электронов от области атомного остова мал и истинный "сильный" потенциал может быть заменён более слабым сглаженным псевдопотенциалом, что соответствует включению в (9) лишь матричных элементов Vgg' с небольшими q=|g-g'|. Для расчёта псевдопотенциала предложен ряд методов, из к-рых наиб. часто используют методы ортогонализованных плоских волн (ОПВ) и присоединённых плоских волн (ППВ). При этом в обоих методах псевдопотенциал оказывается нелокальным, т. е. включает и компоненты Vgg', зависящие от g и g' по отдельности [6, 9].В эмпирич. методе псевдопотенциала Vgg' не рассчитываются, а подбираются, с тем чтобы значения Em(k) в выбранных точках ЗБ совпадали с определёнными экспериментально. Потенциалы Vgg' можно представить как сумму вкладов отд. атомов решётки. Последние записываются в виде произведения структурного фактора, зависящего только от положения атома в ячейке, и формфактора атомных потенциалов, к-рые определяются только типом атома и практически не зависят от соединения, куда этот элемент входит. Это даёт возможность, определив псевдопотенциалы данных атомов из спектров одних веществ. рассчитывать затем спектр др. соединений, образованных ими. Метод сильной связи. В качестве базисных ф-ций выбираются волновые ф-ции изолированных атомов y а(r), и ф-ция нулевого приближения, удовлетворяющая (1), записывается в виде: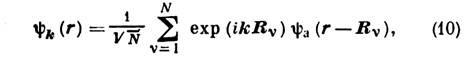
где Rv - координата v -го атома в решётке. При этом перекрытие волновых ф-ций соседних атомов считается малым и соответствующий вклад в энергию E(k )рассчитывается по теории возмущений. Обобщением этого метода является метод линейных комбинаций атомных орбиталей (ЛКАО), где в качестве базиса выбирается набор неск. атомных волновых ф-ций, включая волновые ф-ции возбуждённых состояний [11]. В эмпирич. методе ЛКАО интегралы перекрытия не рассчитываются, а подбираются так, чтобы получаемый спектр E(k )совпадал с экспериментальным, определённым в отд. точках ЗБ, а энергия атомных состояний ya(r )определяется из эксперим. значений потенциалов ионизации атомов или ионов [12].k- р-метод и метод инвариантов. Электрич. и многие др. свойства полупроводников и полуметаллов, в к-рых число свободных носителей заряда мало, определяются лишь спектром вблизи точек экстремума, т. е. у "потолка" валентной зоны и "дна" зоны проводимости. Возможное положение экстремумов, число эквивалентных экстремумов и вид спектров вблизи них зависят от симметрии кристалла. Для расчёта спектра вблизи данного экстремума k0 используется либо теория возмущений (k- р-метод), в к-ром волновая ф-ция электрона в рассматриваемой зоне в точках k№k0 раскладывается по волновым ф-циям всех др. зон в точке k0, либо метод инвариантов, позволяющий непосредственно учесть требования, накладываемые симметрией кристалла [5, 10]. При этом константы, определяющие спектр, находятся из сравнения с эксперим. данными. Для зон, не вырожденных в точке k0, поверхность пост. энергии вблизи неё - эллипсоиды и спектр определяются тензором эффективной массы: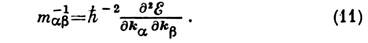
Bсистеме координат, связанных с гл. осями эллипсоида, этот тензор имеет в общем случае 3 компоненты mab-1 = dab/maa и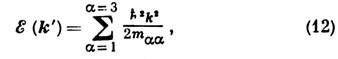
где k'=k-k0. Для электронов вблизи потолка валентной зоны m эaa отрицательны, для дырок т дaa=-т эaa положительны. Если зона вблизи k0 вырождена, то спектр имеет более сложный вид и определяется из решения секулярного ур-ния, порядок к-рого задаётся кратностью вырождения. Аналогичные уравнения используют и для одноврем. описания близко расположенных зон, напр., в узкозонных полупроводниках, что даёт возможность учесть непараболичность спектра, т. е. отступление от закона (12) с увеличением k. Движение электронов во внешних полях. В металлах движение электронов в электрич. E и магн. H полях определяется квазиклассич. ур-ниями:Р p/Рt = F=eE+ e/c[vH], где v=DpE(p).(13)
Из (13) следует, что при движении в поле H сохраняются (составляющая импульса, параллельная Н)pz и полная энергия электрона E(p). Поэтому электрон на поверхности Ферми в магн. поле движется по траектории, представляющей собой её сечение плоскостью pz=const. Для закрытых поверхностей эти сечения замкнуты, для открытых они могут быть замкнутыми и разомкнутыми в зависимости от ориентации Н. Для замкнутых траекторий период обращения электрона:
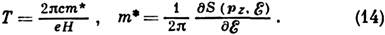
Здесь S - площадь, ограниченная траекторией электрона в плоскости pz=const, величина w с=1/T наз. циклотронной частотой, а т* - циклотронной эфф. массой. При движении по замкнутым траекториям в сильном магн. поле происходит квантование орбит. Расстояние между возникающими Ландау уровнями равно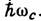 Определив зависимость w с( рz )или площади S(EF, pz )от ориентации H, можно восстановить форму поверхности Ферми. В полупроводниках и диэлектриках с невырожден ными зонами движение носителей также описывается квазиклассич. ур-нием (13).Квантовая теория, использующая Шрёдингера уравнение для спектра, задаваемого ур-нием (12), приводит к тому же выражению для
Определив зависимость w с( рz )или площади S(EF, pz )от ориентации H, можно восстановить форму поверхности Ферми. В полупроводниках и диэлектриках с невырожден ными зонами движение носителей также описывается квазиклассич. ур-нием (13).Квантовая теория, использующая Шрёдингера уравнение для спектра, задаваемого ур-нием (12), приводит к тому же выражению для 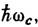 что и ф-ла (14). В случае вырожденных или близких зон в полупроводниках, а также вблизи точек пересечения поверхностей Ферми в металлах квазиклассич. приближение (13) неприменимо и спектр электронов или дырок в электрич. и магн. полях определяется системой связанных ур-ний Шрёдингера, число к-рых определяется кратностью вырождения. В этих случаях уровни Ландау оказываются неэквидистантными. Отступление от квазиклассики для близко расположенных ветвей спектра можно описывать как туннелирование электронов с одной траектории Ландау на другую (см. Пробой магнитный). Границы применимости зонной теории. 3. т. исходит из предположений: а) потенциал кристаллич. решётки строго периодичен; б) взаимодействие между свободными электронами может быть сведено к одноэлектронному самосогласованному потенциалу, а оставшаяся часть рассмотрена методом теории возмущений; в) взаимодействие с фононами слабое и может быть рассмотрено по теории возмущений (см. Электроннофононное взаимодействие). В неупорядоченных системах условие а) не выполняется. Однако т. к. размытие атомных уровней связано с перекрытием волновых ф-ций соседних атомов, то и в неупорядоченных средах, в т. ч. в жидкостях, образуются разрешённые зоны и квазизапрещённые, с резко пониженной плотностью состояний. В неупорядоченных средах имеются два типа состояний электрона - локализованные и делокализованные. Локализация, связанная с разупорядочением решётки, наз. андерсеновской, а граничная энергия между локализованными и делокализованными состояниями - уровнем локализации. Если уровень Ферми в металле или сильно легированном полупроводнике проходит выше уровня локализации, то их проводимость носит металлич. характер (см. Аморфные металлы). В обратном случае проводимость осуществляется путём активированных перескоков между локализованными состояниями или тепловым забросом электронов выше уровня локализации. Условие б) хорошо выполняется в полупроводниках и диэлектриках с малым числом свободных электронов, когда взаимодействие между ними мало и может быть учтено как электрон-электронное рассеяние. В металлах, где число свободных электронов велико, взаимодействие с осн. массой электронов учитывается самосогласованным одноэлектронным потенциалом. Взаимодействие с электронами, находящимися в тонком слое вблизи поверхности Ферми, может быть учтено в рамках теории ферми-жидкости, в к-рой в качестве элементарных возбуждений рассматриваются заряж. квазичастицы - фермионы, описывающие самосогласованное движение всей системы электродов. Электрон-электронное взаимодействие приводит, как правило, лишь к перенормировке спектра. Исключение составляют кристаллы с узкими зонами, где энергия отталкивания двух электронов на одном узле превышает ширину зоны. Если в таких кристаллах число электронов равно числу атомов, они являются диэлектриками, даже если число мест в зоне (с учётом спина) больше числа атомов. При изменении ширины разрешённой зоны в результате сближения атомов происходит переход к металлич. проводимости (переход Мотта).Наряду с возбуждениями фермиевского типа в многоэлектронной системе в результате электрон-электронного взаимодействия возникают возбуждения - бозоны, не связанные с переносом заряда ( плазмоны, спиновые волны). В этих колебаниях могут участвовать электроны и частично заполненных, и полностью заполненных зон. В полупроводниках и диэлектриках в результате взаимодействия электрона зоны проводимости и дырки валентной зоны образуются связанные состояния Ванье - Мотта экситоны. В молекулярных кристаллах и диэлектриках возбуждённыесостояния атомов или молекул, перемещающиеся по кристаллу, образуют Френкеля экситоны. Волновая ф-ция экситона удовлетворяет ф-ле (1); области разрешённых значений энергии экситона называются экситонными зонами. Условие в) выполняется практически во всех металлах, где электрон-фононное взаимодействие ослабляется в результате его экранирования свободными электронами, и во мн. полупроводниках. В полярных диэлектриках и полупроводниках с достаточно большой степенью ионной связи и большой эфф. массой носителей последние, поляризуя решётку, образуют автолокализов. состояния - поляроны. Различают поляроны большого радиуса, у к-рых область локализации R п намного превышает постоянную решётки а, и малого радиуса с R п@ а. Автолокализов. состояния малого радиуса образуются и в неполярных диэлектриках, напр, в кристаллах инертных газов (см. Автолокализация), при этом, как правило, происходит автолокализация только дырок. Движение поляронов малого радиуса при низких темп-pax осуществляется по очень узкой поляронной зоне, а при более высоких - путём активированных перескоков от узла к узлу. Лит.:1) Бете Г., 3 о м м е р ф е л ь д А., Электронная теория металлов, пер. с нем., Л.- М., 1938; 2) Абрикосов А. А., Основы теории металлов, М., 1987; 3) Киттель Ч., Квантовая теория твердых тел, пер. с англ., М., 1967; 4) Каллуэй Д ж., Теория энергетической зонной структуры, пер. с англ., М., 1969; 5) Вир Г. Л., Пикус Г. Е., Симметрия и деформационные эффекты в полупроводниках, М., 1972; 6) Dimmock J. О., The calculation of electronic energy bands by the augmented plane wave method, "Solid State Phys.", 1971, v. 26, p. 129; 7) Xappисон У. А., Электронная структура и свойства твердых тел, пер. с англ., т. 1-2, М., 1983; 8) Xейне В., Коэн М., Уэйр Д., Теория псевдопотенциала, пер. с англ., М., 1973; 9) 3айман Д ж., Принципы теории твердого тела, пер. с англ., М., 1974; 10) Цидильковский И. М., Зонная структура полупроводников, М., 1978; 11) Heine V., Electronic structure from the point of view of the local atomic environment, "Solid State Phys.", 1980, y. 35, p. 1; 12) В u 1 1 e t t D. W., The Renaissance and quantitative development of the tightbinding method, там же, р. 129. Г. Е. Пикус.
что и ф-ла (14). В случае вырожденных или близких зон в полупроводниках, а также вблизи точек пересечения поверхностей Ферми в металлах квазиклассич. приближение (13) неприменимо и спектр электронов или дырок в электрич. и магн. полях определяется системой связанных ур-ний Шрёдингера, число к-рых определяется кратностью вырождения. В этих случаях уровни Ландау оказываются неэквидистантными. Отступление от квазиклассики для близко расположенных ветвей спектра можно описывать как туннелирование электронов с одной траектории Ландау на другую (см. Пробой магнитный). Границы применимости зонной теории. 3. т. исходит из предположений: а) потенциал кристаллич. решётки строго периодичен; б) взаимодействие между свободными электронами может быть сведено к одноэлектронному самосогласованному потенциалу, а оставшаяся часть рассмотрена методом теории возмущений; в) взаимодействие с фононами слабое и может быть рассмотрено по теории возмущений (см. Электроннофононное взаимодействие). В неупорядоченных системах условие а) не выполняется. Однако т. к. размытие атомных уровней связано с перекрытием волновых ф-ций соседних атомов, то и в неупорядоченных средах, в т. ч. в жидкостях, образуются разрешённые зоны и квазизапрещённые, с резко пониженной плотностью состояний. В неупорядоченных средах имеются два типа состояний электрона - локализованные и делокализованные. Локализация, связанная с разупорядочением решётки, наз. андерсеновской, а граничная энергия между локализованными и делокализованными состояниями - уровнем локализации. Если уровень Ферми в металле или сильно легированном полупроводнике проходит выше уровня локализации, то их проводимость носит металлич. характер (см. Аморфные металлы). В обратном случае проводимость осуществляется путём активированных перескоков между локализованными состояниями или тепловым забросом электронов выше уровня локализации. Условие б) хорошо выполняется в полупроводниках и диэлектриках с малым числом свободных электронов, когда взаимодействие между ними мало и может быть учтено как электрон-электронное рассеяние. В металлах, где число свободных электронов велико, взаимодействие с осн. массой электронов учитывается самосогласованным одноэлектронным потенциалом. Взаимодействие с электронами, находящимися в тонком слое вблизи поверхности Ферми, может быть учтено в рамках теории ферми-жидкости, в к-рой в качестве элементарных возбуждений рассматриваются заряж. квазичастицы - фермионы, описывающие самосогласованное движение всей системы электродов. Электрон-электронное взаимодействие приводит, как правило, лишь к перенормировке спектра. Исключение составляют кристаллы с узкими зонами, где энергия отталкивания двух электронов на одном узле превышает ширину зоны. Если в таких кристаллах число электронов равно числу атомов, они являются диэлектриками, даже если число мест в зоне (с учётом спина) больше числа атомов. При изменении ширины разрешённой зоны в результате сближения атомов происходит переход к металлич. проводимости (переход Мотта).Наряду с возбуждениями фермиевского типа в многоэлектронной системе в результате электрон-электронного взаимодействия возникают возбуждения - бозоны, не связанные с переносом заряда ( плазмоны, спиновые волны). В этих колебаниях могут участвовать электроны и частично заполненных, и полностью заполненных зон. В полупроводниках и диэлектриках в результате взаимодействия электрона зоны проводимости и дырки валентной зоны образуются связанные состояния Ванье - Мотта экситоны. В молекулярных кристаллах и диэлектриках возбуждённыесостояния атомов или молекул, перемещающиеся по кристаллу, образуют Френкеля экситоны. Волновая ф-ция экситона удовлетворяет ф-ле (1); области разрешённых значений энергии экситона называются экситонными зонами. Условие в) выполняется практически во всех металлах, где электрон-фононное взаимодействие ослабляется в результате его экранирования свободными электронами, и во мн. полупроводниках. В полярных диэлектриках и полупроводниках с достаточно большой степенью ионной связи и большой эфф. массой носителей последние, поляризуя решётку, образуют автолокализов. состояния - поляроны. Различают поляроны большого радиуса, у к-рых область локализации R п намного превышает постоянную решётки а, и малого радиуса с R п@ а. Автолокализов. состояния малого радиуса образуются и в неполярных диэлектриках, напр, в кристаллах инертных газов (см. Автолокализация), при этом, как правило, происходит автолокализация только дырок. Движение поляронов малого радиуса при низких темп-pax осуществляется по очень узкой поляронной зоне, а при более высоких - путём активированных перескоков от узла к узлу. Лит.:1) Бете Г., 3 о м м е р ф е л ь д А., Электронная теория металлов, пер. с нем., Л.- М., 1938; 2) Абрикосов А. А., Основы теории металлов, М., 1987; 3) Киттель Ч., Квантовая теория твердых тел, пер. с англ., М., 1967; 4) Каллуэй Д ж., Теория энергетической зонной структуры, пер. с англ., М., 1969; 5) Вир Г. Л., Пикус Г. Е., Симметрия и деформационные эффекты в полупроводниках, М., 1972; 6) Dimmock J. О., The calculation of electronic energy bands by the augmented plane wave method, "Solid State Phys.", 1971, v. 26, p. 129; 7) Xappисон У. А., Электронная структура и свойства твердых тел, пер. с англ., т. 1-2, М., 1983; 8) Xейне В., Коэн М., Уэйр Д., Теория псевдопотенциала, пер. с англ., М., 1973; 9) 3айман Д ж., Принципы теории твердого тела, пер. с англ., М., 1974; 10) Цидильковский И. М., Зонная структура полупроводников, М., 1978; 11) Heine V., Electronic structure from the point of view of the local atomic environment, "Solid State Phys.", 1980, y. 35, p. 1; 12) В u 1 1 e t t D. W., The Renaissance and quantitative development of the tightbinding method, там же, р. 129. Г. Е. Пикус.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.