Akademik

- релятивистские суперсимметричные протяжённые объекты. С. являются обобщением понятия бозонной релятивистской струны (см. Струна релятивистская) с включением фермионных степеней свободы. В зависимости от вида граничных условий для фермионов различают струны Рамона (P. Ramond, 1971) и Неве - Шварца (A. Neveu, J. Schwarz, 1971). При этом суперсимметрия может быть реализована двояким образом: как двумерная суперсимметрия на мировой поверхности, заметаемой струной при своём движении в пространстве-времени, либо как пространственно-временная суперсимметрия. Последний случай отвечает струне Грина - Шварца (М. Green, J. Schwarz, 1982).

При квантовании С. представляет собой бесконечную последовательность нормальных мод - последовательность массивных состояний в квантовой теории поля. Расщепление масс Dm² пропорционально натяжению струны Т. В теории С. T~(10¹⁹ ГэВ)² [в системе единиц 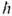=с= 1 ]. Спектр масс начинается с нуля и, в отличие от теории бозонной струны, не содержит тахиона (т. е. состояния с мнимой массой). Последовательное квантование в плоском пространстве-времени оказывается возможным только в критич. размерности. Для бозонной струны D _кр = 26, для фермионной - D _кр=10.

Струны бывают о т к р ы т ы м и и з а м к н у т ы м и. Открытые струны в качестве низших безмассовых состояний содержат частицы спина 1-кванты Янга-Миллса поля, замкнутые - частицы спина 2 - гравитоны, а в случае С. содержат и их суперпартнёры спина ³/₂ - гравитино. На этом пути в теории С. возникает локальная квантовая теория поля, объединяющая гравитацию и поля Янга - Миллса - переносчики всех взаимодействий [Дж. Шерк (J. Scherk) и Дж. Шварц, 1974].

На расстояниях, много больших платовской длины(~10^-33 см), или при энергиях, много меньших планков-ской массы(~ 10¹⁹ ГэВ), массивные состояния отщепляются и возникает эфф. локальная теория поля (супергравитация и суперсимметричная янг-миллсовская теория с фиксированными параметрами и составом частиц). При этом наблюдаемые частицы (кварки, лептоны, калибровочные векторные бозоны и т. д.) должны быть среди безмассовых возбуждений (m<<10¹⁹ ГэВ).

Различают след. теории С.

Тип I, к к-рому относятся разомкнутые неориентированные струны с N=1суперсимметрией. При матем. описании с концами струны ассоциируются матрицы фундам. представления калибровочной группы, причём согласованная квантовая теория неориентированных струн допускает только классич. группы SO(n )и Sp(n). Как оказывается, требование сокращения аномалий и расходимостей оставляет только группу SO(32). Взаимодействуя, открытые струны образуют замкнутые конфигурации - синглеты калибровочной группы. В пределе малых энергий С. типа Г приводят к (D=10) суперсимметричной теории Янга - Миллса и N=1 супергравитации.

Тип II, к к-рому относятся замкнутые ориентированные струны с N=2 суперсимметрией. Здесь нет группы внутренних симметрии. В пределе низких энергий получается (D=10) N=2 теория супергравитации.

Гетерозисная (гетеротическая) струна (биол. термин "гетерозис" означает явление усиления положит. свойств гибрида по сравнению с исходными образцами) - замкнутая ориентированная струна, к-рая является гибридом 26-мерной бозонной струны и 10-мерной фермионной струны типа II. Это связано с тем, что в замкнутой струне левые и правые моды существуют независимо. В гетерозисной струне они входят несимметричным образом: правые моды соответствуют 10-мерной фермионной струне, а левые- 26-мерной бозонной струне, причём лишние 16 измерений компактифицированы на 16-мерный тор. При этом возникает калибровочная группа, решётка корней к-рой идентифицируется с решёткой дискретных импульсов, сопряжённых с внутр. измерениями. Возникающая группа имеет ранг 16 и размерность 496. Такими группами являются группа SO(32) и E₈ 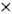Е₈.[Д. Гpocc (D. Gross) и др., 1985].

Существуют также версии гетерозисной струны, где компактификация происходит непосредственно из 26 в 4 измерения для левых мод и из 10 в 4 для правых [К. Нарайн (К. Narain), 1986]. Калибровочная группа при этом имеет ранг 22. Других ограничений на калибровочную группу в этом случае не возникает. Поэтому таких теорий существует огромное множество. Полной их классификации не существует.

Взаимодействие струн носит локальный характер, несмотря на то, что сами они являются протяжёнными объектами. В первично-квантованной формулировке теории взаимодействие струн описывается квантовыми флук-туациями мировой поверхности струны, причём свободная струна соответствует поверхности без особенностей, а взаимодействующая - топологически нетривиальным поверхностям, содержащим "дырки" (А. М. Поляков, 1981) [см. рис, 1, 2]. Во вторично-квантованном формализме для описания струн используются функционалы на мировой поверхности. При этом лагранжиан свободной струны квадратичен по этим функционалам, а взаимодействия струн описываются локальными кубическими по функционалам членами. Для открытых струн возможны также вершины четвёртого порядка. Вершины высших порядков отсутствуют [Э. Виттен (Е. Witten) и др., 1986].

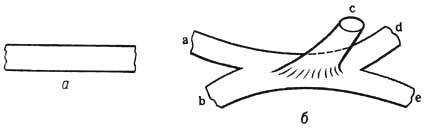
Рис. 1. а - Схематическое изображение свободной открытой струны; б- взаимодействие открытых струн с образованием замкнутой струны. Открытые струны а и b, соединяясь своими концами, образуют одну открытую струну, которая порождает замкнутую стру ну с и открытые струны d и е.

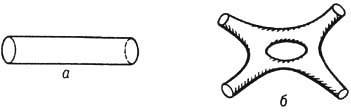
Рис. 2. а- Схематическое изображение свободной замкнутой струны; б - взаимодействие замкнутых струн с образованием "дырки".

Взаимодействуя, струны могут рассеиваться, рождать новые струны, а также испускать точечные частицы. В эффективной локальной теории этому соответствуют всевозможные взаимодействия локальных полей.

Теория С. свободна от квантовых калибровочных и гра-витац. аномалий и конечна в однопетлевом приближении. Это требование в случае С. типа I выделяет калибровочную группу SO(32), а также удовлетворяется и в теории гетерозисной струны для групп SO(32) и Е₈ Е₈. Т. о., в этом подходе калибровочная группа фиксируется условием самосогласованности квантовой теории (Грин и Шварц, 1984).

Переход к наблюдаемой размерности пространства-времени (D =4)в теории С. достигается путём компактифика-ции "лишних" пространственных измерений на расстояниях порядка планковской длины. Установлено, что эффективная локальная теория содержит дополнительные, т. н. чжэнь-саймоновские члены [Ш. Чжэнь (S. Chern), Дж. Саймоне (J. Simons)], к-рые совместно с высшими производными в ур-ниях движения приводят к спонтанной компактифи-кации дополнит. измерений. При этом происходит сужение калибровочной группы до группы симметрии низкоэнер-гегич. теории. Феноменологич. следствия теории С. во многом зависят от механизма компактификации.

Развитие суперструнной картины показало, что эта теория является плодотворным обобщением локальных теорий поля. На таком пути, возможно, удастся построить самосогласованную квантовую теорию всех фундам. взаимодействий. Однако теория С. далека от завершения. Так, напр., открытие явления дуальности между теориями С. привело к пониманию того, что перечисленные типы теорий С. являются разл. предельными формулировками одной теории.

Лит.: Барбашов Б. М., Нестеренко В. В., Суперструны - новый подход к единой теории фундаментальных взаимодействий, "УФН", 1986, т. 150, в. 4, с. 489; Казаков Д. И., Суперструны, или За пределами стандартных представлений, там же, с. 561; Грин М., Теории суперструн в реальном мире, там же, с. 577; Энтони С., Суперструны: всеобъемлющая теория?, там же, с. 579; Грин М., Шварц Дж., Виттен Э., Теория суперструн, пер. с англ., т. 1-2, М., 1990. Д. И. Казаков.