Akademik

- теплоёмкость твёрдого тела, обусловленнаяатомной подсистемой, в частности кристаллич. решёткой. Р. т. является частьютеплоёмкости твёрдого тела. Термин «Р. т.» может относиться не только кидеальным кристаллам, но и к кристаллам с дефектами решётки или примесями, к некристаллич. твёрдым телам (аморфным веществам, стёклам).

Различие между Р. т. при пост, давлении ( С _р )ц припост. объёме (Су) мало: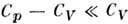. При Т - ОК это является следствием теоремы Нернста (см. Третьеначало термодинамики), а при произвольных Т обусловлено малостьютепловой энергии (kT )относительно энергии связи атомов в твёрдомтеле. Величина и температурная зависимость Р. т. С определяются энергетич. спектром 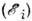колебании атомной подсистемы (см. Колебания кристаллической решётки):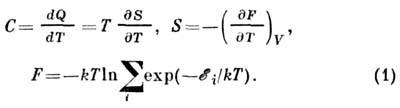

Здесь S - энтропия, F - Гельмгольца энергия. Величина dS/дТ вычисляется при пост. давлении либо при пост, объёме, в зависимостиот того, какая из величин С _р или С _V подлежитопределению.

Спектр колебаний атомной подсистемы зависит от её хим. состава и структурыи для реальных твёрдых тел сложен. Теория Р. т. основана на упрощающихпредположениях о виде колебат. спектра. При высоких Т, когда возбужденывсе 3N степеней свободы твёрдого тела, содержащего N атомов, из теоремы о равнораспределении энергии следует, что на каждую колебат. степень свободы приходится энергия kТ, и потому С= 3Nk. Этот результат соответствует эксперим. данным для простых кристаллич. решёток (элементы и простые соединения, см. Дюлонга и Пти закон). Длясложных соединений предельное значение С= 3Nk с повышением Т обычно не достигается, т. к. раньше происходит их плавление илиразложение.

При понижении темп-ры Р. т. убывает, благодаря «вымораживанию» колебанийс энергиями 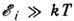Простейшей моделью, описывающей этот процесс, является модель Эйнштейна, в к-рой всем степеням свободы твёрдого тела сопоставляются одномодовыегармонич. осцилляторы с частотой 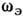.В этом случае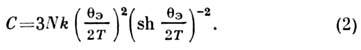

Величину 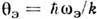называют Эйнштейна температурой.

В области низких Т играют роль лишь колебания с малыми энергиями , т. е. с малыми частотами 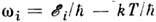. Это звуковые колебания, длина волны к-рых заметно превышает постояннуюрешётки а при условии 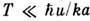,где и - скорость звука. Число длинноволновых звуковых колебанийв интервале частот dw в объёме V трёхмерного кристалла равно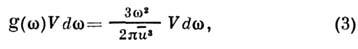

где 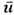-среднее по различным кристаллографич. направлениям, g - плотность распределенияколебаний но частотам. С учётом (3) из (1) следует:

Р. т., пропорциональная Т ³, наблюдается при низкихтемп-pax для многих твёрдых тел (см. Девая закон теплоёмкости). Этотзакон фактически начинает выполняться при 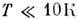для простых решёток и при значительно меньших Т для тел со сложнойрешёткой. Интерполяция между пределами низких и высоких темп-р в кристаллахдаётся Дебая теорией твёрдого тела. Она основана на предположении, что частоты распределены по закону (3) на всём протяжении спектра, к-рыйобрывается при нек-рой максимальной дебаевской частоте 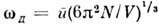.При этом соотношение (1) даёт: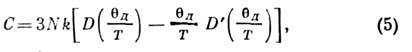

где 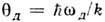- Дебая температура, D(x)=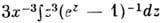ф-ция Дебая (рис. 1). Критерием применяемости этой теории для Р. т. являетсясоотношение Т и 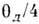:Р. т. можно считать постоянной при 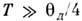и пропорциональной Т ³ при 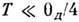. Ф-ла (5) передаёт ход С(Т )лишь для простых решёток; к телам сболее сложной структурой она неприменима, т. к. их спектр колебаний сложен.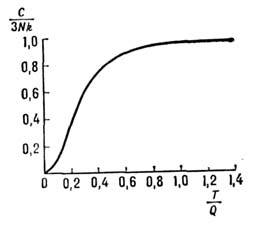

Рис. 1. Зависимость решёточной теплоёмкости от температуры в моделиДебая.

В кристаллах «слоистого» или «цепочечного» типа ( квазиодномерныесоединения и квазидвумерные соединения )спектр звуковых колебанийхарактеризуется не одной, а неск.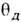,различными по порядку величины. Закон Т ³ для Р. т. имеетпри этом место лишь при Т, малых по сравнению с наименьшей из дебаевскихтемп-р, в промежуточных же областях Т возникают др. законы. Еслиобозначить через 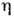отношение энергии связи между слоями к энергии связи между атомами в слоях, то закон Т ³ для Р. т. будет иметь место лишь при 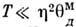, где 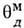-наибольшая из 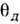.В области 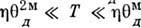имеют место зависимости: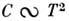для слоистых и 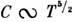для цепочечных кристаллов. При 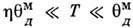имеют место зависимост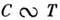и и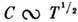

Влияние дефектов. Величина и температурная зависимость Р. т. кристалловзависят от наличия дефектов и примесей. К увеличению низкотемпературнойР. т. при 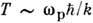могут привести резонансные квазилокальные колеоания с частотами 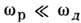,к-рые возникают благодаря введению тяжёлых примесей или дефектов. ЛокальныеВЧ-колебания 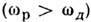слабо влияют на Р. т. Заметный вклад в низкотемпературную Р. т. могут даватьтакже т. н. ориентац. дефекты (дипольные центры) и нецентральные ионы.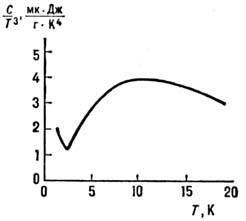

Рис. 2. Зависимость С(Т) аморфного кварца (а = SiO₂).Рост в зависимости С(Т) левее минимума обусловлен линейной зависимостьютеплоёмкости от Т.

Решёточная теплоёмкость некристаллических веществ (аморфных или стеклообразныхтвёрдых тел, полимеров, ионных суперпроводников) при низких Т кардинальноотличается от Р. т. кристаллов. При Т< 1 К Р. т. этих веществсущественно превышает Р. т. кристаллов и зависит от Т приблизительнолинейно. При Т~ 10 К в зависимости С(Т )появляется максимум, свидетельствующий об избыточной (по сравнению с дебаевской) теплоёмкости(рис. 2). Такое поведение и величина Р. т. слабо зависят от хим. составаи типа проводимости некристаллич. веществ, являясь в этом смысле универсальными. Так, зависимость 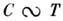наблюдается не только в диэлектрических и полупроводниковых стёклах, но и в металлических стёклах. В последнем случае она экспериментальноотделяется от электронной теплоёмкости по наблюдению ц сверхпрово-дящемсостоянии, когда электронная теплоёмкость пренебрежимо мала.

Линейная зависимость от темп-ры 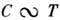объясняется моделью двухуровневых систем, отвечающих туннельным состоянияматомов в двухъямных потенциалах, существование к-рых связано с неупорядоченностьюсистемы (см. Неупорядоченные системы). Постулируется равномерноераспределение энергий с плотностью 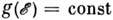.Это приводит к соотношению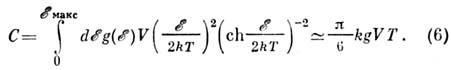

Предполагается, что верхняя граница спектра 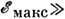kT. Тепловое возбуждение двухуровневых систем происходит за времярелаксации, величина к-рого экспоненциально зависит от параметров барьерав двухъямном потенциале. Разброс значений этих параметров в некристаллич. веществе приводит к появлению экспоненциально широкого спектра времен релаксации. В результате возникает логарифмически слабая зависимость измеряемой Р. т. от времени эксперимента.

Лит.: Ландау Л. Д., Л и ф ш и ц Е. М., Статистическая физика, ч. 1, 3 изд., М., 1976; К и т т е л ь Ч., Введение в физику твердого тела, пер. с англ., М., 1978; Amorphous solids. Low-temperature properties, ed.by W. A. Phillips, B.- [a. o.], 1981. В. Г. Карпов.