Akademik

СПЕКТР колебаний

СПЕКТР колебаний: совокупность гармонич. колебаний, на к-рые может быть разложено данное сложное колебат. движение. Математически такое движение представляется в виде периодической, но негармонич. ф-ции f(t) с частотой w. Эту ф-цию можно представить в виде ряда гармонич. функций: f(t)=SAncosnwt с частотами поз, кратными осн. частоте (где An — амплитуды гармонич. функций, t — время, n — номер гармоники). Чем сильнее исходное колебание отличается от гармонического, тем богаче его С., тем больше составляющих обертонов (гармоник) содержится в разложении и тем больше их амплитуды. В общем случае С. колебания содержит бесконечный ряд гармоник, амплитуды к-рых быстро убывают с увеличением их номера, так что практически приходится принимать во внимание только нек-рое конечное число обертонов. Процессы, не имеющие строгой периодичности или непериодические, могут представляться в виде суммы гармонич. компонент с некратными частотами или в виде суммы (интеграла) бесконечного числа составляющих со сколь угодно близкими частотами (непрерывный С.). С. звука выражает его частотный состав и получается в результате анализа звука. С. звука представляют обычно на координатной плоскости.

Рис. 1. Линейчатый спектр, полученный при сложении двух периодич. волн с осн. частотами f'0 и f"0.

где по оси абсцисс отложена частота f, а по оси ординат — амплитуда А или интенсивность I гармонич. составляющей звука с данной частотой. Чистые тона, звуки с периодич. формой волны, а также звуки, полученные при сложении неск. периодич. волн, обладают линейчатыми спектрами (рис. 1). Акустические шумы, одиночные импульсы, затухающие звуки имеют сплошной спектр (рис. 2).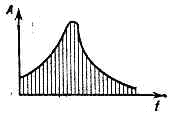

Рис. 2. Сплошной спектр затухающего колебания.

Частотные компоненты спектра импульса акустического прямоуг. формы с заполнением несущей частотой f0 сосредоточены в осн. вблизи этой частоты в полосе шириной 7/Т, где Т — длительность импульса.

СПЕКТР КОЛЕБАНИЙ: - совокупность гармонич. колебаний, на к-рыеможет быть разложено сложное колебат. движение (см. Фурье анализ). Математическитакое движение представляется в виде периодической, но негармонич. ф-ции f(t )с частотой w. Эту ф-цию можно представить в виде ряда гармонич. ф-ций: f(t)=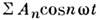с частотами nw, кратными осн. частоте (где А _п - амплитудыгармонич. ф-ций, t - время, п- номер гармоники). Чем сильнееисходное колебание отличается от гармонического, тем богаче его спектр, тем больше составляющих обертонов (гармоник) содержится в разложении итем больше их амплитуды. В общем случае С. к. содержит бесконечный рядгармоник, амплитуды к-рых быстро убывают с увеличением их номера, так чтопрактически приходится принимать во внимание только нек-рое конечное числообертонов. Процессы, не имеющие строгой периодичности, или непериодическиемогут представляться в виде суммы гармонич. компонентов с некратными частотамиили в виде суммы (интеграла) бесконечного числа составляющих со сколь угодноблизкими частотами (непрерывный спектр).