Akademik

механики. 1) Лагранжа уравнения 1-го рода - дифференциальные ур-ния движения механич. системы, к-рые даны в проекциях на прямоугольные координатные оси и содержат т. н. множители Лагранжа. Получены Ж. Лагранжем в 1788. Для голономной системы, состоящей из п материальных точек, на к-рую наложено k связей вида

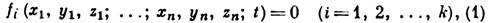
Л. у. 1-го рода имеют вид

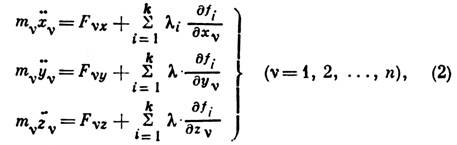
где m_v - массы точек системы; 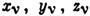- координаты этих точек; 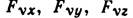- проекции приложенных к каждой точке активных сил; 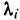- неопределённые множители, пропорциональные реакциям соответствующих связей; t- время. Аналогичные ур-ния могут составляться и для неголономных систем. Ур-ния (2) совместно с (1) дают систему 3n+k дифференциальных ур-ний, из к-рых находятся З n неизвестных ф-ций 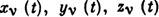', дающих закон движения точек системы, и k множителей 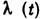, позволяющих определить проекции реакций связей по ф-лам

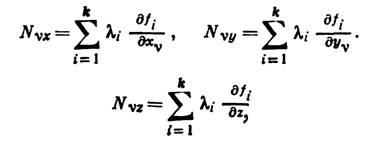
Для отыскания закона движения ур-ниями (2) пользуются редко, т. к. интегрирование системы З n+k ур-ний, когда п велико, связано с большими трудностями. Однако если закон движения будет найден другим путём (напр., с помощью ур-ний Лагранжа 2-го рода), то по ур-ниям (2), в к-рых левые части известны, можно определять реакции связей.

2) Лагранжа уравнения 2-го рода - дифференциальные ур-ния движения механич. системы, в к-рых параметрами, определяющими положение системы, являются независимые между собой обобщённые координаты. Для голономных систем Л. у. 2-го рода имеют в общем случае вид

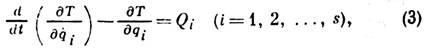
где q_i - обобщённые координаты, число к-рых равно числу s степеней свободы системы, q_i - обобщённые скорости, Q_i - обобщённые силы.

Для составления ур-ний (3) надо, выбрав q , определить кинетич. энергию системы в её движении относительно инерциалъной системы отсчета и выразить эту величину явно через q_i и q_i, т. е. найти Т (q_i,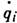, t); время войдёт сюда при нестационарных связях. Значения Q_i находятся по заданным (активным) силам, в число к-рых при неидеальных связях включают и силы трения. С матем. точки зрения ур-ния (3) представляют собой систему обыкновенных дифференциальных ур-ний 2-го порядка относительно координат q_i; интегрируя эти ур-ния и определяя постоянные интегрирования по нач. условиям, находят q_i(t), т. е. закон движения системы в обобщённых координатах.

По сравнению с ур-ниями в декартовых координатах (см., напр., ур-ния Лагранжа 1-го рода) ур-ния (3) обладают тем важным преимуществом, что число их равно числу степеней свободы системы и не зависит от кол-ва входящих в систему материальных частиц или тел; кроме того, при идеальных связях из ур-ний (3) автоматически исключаются все наперёд неизвестные реакции связей. Л. у. 2-го рода, дающими весьма общий и притом достаточно простой метод решения задач, широко пользуются для изучения движения разл. механич. систем, в частности в динамике механизмов и машин, в теории гироскопа, в теории колебаний и др.

Для неголономной системы, на к-рую, кроме геом. связей, учитываемых выбором координат q_i, наложено ещё k дифференциальных связей, выражаемых равенствами

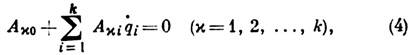
Л. у. 2-го рода принимают вид

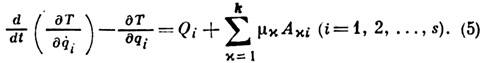
Ур-ния (5) совместно с (4) дают возможность определить s неизвестных координат q_i н k наперёд неизвестных множителей 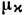как ф-ций времени.

В физике особое значение имеет та форма Л. у., к-рую они принимают в случае голономной системы, находящейся под действием одних только потенц. сил (см. Консервативная система). Если ввести ф-цию Лагранжа (лагранжиан) L, равную в этом случае разности между кинетической Т и потенциальной П энергиями системы:

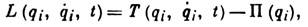
то, т. к. для потепц. сил 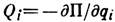, равенства (3) примут вид

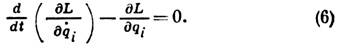
Ур-ния в форме (6) обычно и наз. в физике ур-ниями Лагранжа. Преимущество этих ур-ний состоит в том, что они позволяют изучить движение механич. системы, зная для неё одну только ф-цию L, полностью характеризующую систему. Такая форма ур-ний имеет место не только для консервативных систем. Если обобщённые силы можно представить через нек-рый "обобщённый потенциал" U(q_i, 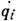)в виде

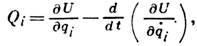
то ур-ния (3) представляются тоже в виде (6), где L= T+U. Напр., для заряж. частицы массы m с зарядом 9, движущейся в эл.-магн. ноле, к-рое характеризуется векторным А и скалярным 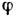потенциалами, существует "обобщённый потенциал"

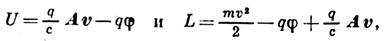
где 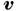- скорость частицы, с - скорость света.

Область приложения ур-ний (6) оказывается ещё более широкой благодаря их связи с наименьшего действия принципом. Согласно этому принципу, для истинного движения системы величина 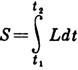, наз. действием, имеет экстремум, условие существования к-рого состоит в том, что ф-ция L должна удовлетворять ур-ниям Эйлера, совпадающим с ур-ниями (6). Отсюда следует, что ур-ния вида (6) справедливы для любой физ. системы (непрерывная среда, гравитац. или эл.-магн. поле и др.), к-рая характеризуется соответствующей ф-цией Лагранжа и подчиняется вариационному принципу, аналогичному принципу наим. действия.

Для среды или поля, представляющих собой систему с бесконечным числом степеней свободы, роль обобщённых координат q_i играют такие величины, как смещение частицы, плотность, потенциал и т. п., зависящие в общем случае от координат х, у, z точек среды (поля) и от времени; поэтому для такой среды (поля) q_i =q_i ( х, у, z, t). Характеристикой системы в этих случаях служит удельная (отнесённая к единице объёма) ф-ция Лагранжа, или лагранжиан

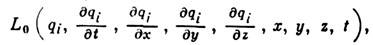
и Л. у. для среды (поля) принимают вид

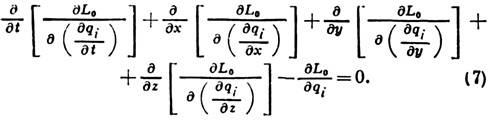
Ур-ния (7), в отличие от (3) или (6), представляют собой систему ур-ний в частных производных; число их равно числу величин q_i.

Примером приложения ур-ний (7) к упруго деформируемой среде может служить задача о продольных вдоль оси х колебаниях призматич. стержня. В этом случае имеется одна обобщённая координата q₁=u(x, t), где и - продольное смещение частиц стержня, и ф-ция L₀, составляемая как разность удельных кинетической и потенциальной энергий, имеет вид

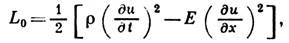
где 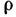- плотность среды, Е - модуль упругости при растяжении. Подстановка этого значения L₀ в (7) даёт ур-ние продольных упругих колебаний:

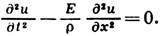
Др. примером может служить эл.-магн. поле в вакууме, для к-рого в качестве четырёх обобщённых координат можно принять компоненты А _х, А _у, А _z векторного потенциала А и скалярный потенциал . В этом случае

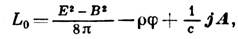
где Е - напряжённость электрич. поля, В - магн. индукция, j - плотность тока, 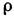- уд. заряд. При этом значении L₀ равенства (7) дают ур-ния Максвелла.

Л. у. в виде (6) сохраняют смысл и при движениях со скоростями, сравнимыми со скоростью света, но при этом в выражение ф-ции L вместо кинетич. энергии частицы входит величина - 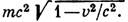См. также Лагранжев формализм.

Лит.:1) Лагранж Ж., Аналитическая механика, пер. с франц., 2 изд., т. 1-2, М.- Л., 1950; 2) Жуковский Н. Е., Теоретическая механика, 2 изд., М.- Л., 1952; 3) Суслов Г. К., Теоретическая механика, 3 изд., М.- Л., 1946: 4) Лойцянский Л. Г., Лурье А. И., Курс теоретической механики, 6 изд., т. 2, М., 1983; 5) Ландау Л. Д., Лифшиц Е. М., Механика, 4 изд., М., 1988, гл. 1; 6) Голдстейн Г., Классическая механика, пер. с англ., 2 изд., М., 1975, гл. 1, 2, 11. С. М. Тарг.