- ЭНТРОПИЯ
-
(от греч. entropia — поворот, превращение), понятие, впервые введённое в термодинамике для определения меры необратимого рассеяния энергии. Э. широко применяется и в др. областях науки: в статистической физике как мера вероятности осуществления к.-л. макроскопич. состояния; в теории информации как мера неопределённости к.-л. опыта (испытания), к-рый может иметь разные исходы. Эти трактовки Э. имеют глубокую внутр. связь. Напр., на основе представлений об информац. Э. можно вывести все важнейшие положения статистич. физики.В термодинамике понятие «Э.» было введено нем. физиком Р. Клаузиусом (1865), к-рый показал, что процесс превращения теплоты в работу подчиняется определ. физ. закономерности — второму началу термодинамики, к-рое можно сформулировать строго математически, если ввести особую ф-цию состояния —Э. Так, для термодинамич. системы, совершающей квазистатически (бесконечно медленно) циклич. процесс, в к-ром система последовательно получает малые кол-ва теплоты dQ при соответствующих значениях абс. темп-ры Т, интеграл от «приведённого» кол-ва теплоты dQ/T по всему циклу равен нулю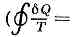 =0 — т. н. равенство Клаузиуса). Это равенство, эквивалентное второму началу термодинамики для равновесных процессов, Клаузиус получил, рассматривая произвольный циклич. процесс как сумму очень большого (в пределе бесконечно большого) числа элементарных Карно циклов. Математически равенство Клаузиуса необходимо и достаточно для того, чтобы выражениеdS=dQ/T (1)представляло собой полный дифференциал ф-ции состояния S, назв. «Э.» (дифф. определение Э.). Разность Э. системы в двух произвольных состояниях А и В (заданных, напр., значениями темп-р и объёмов) равна:SB-SA=?BAdQ/T (2)(интегр. определение Э.). Интегрирование здесь ведётся вдоль пути любого квазистатич. процесса, связывающего состояния А и В, при этом, согласно равенству Клаузиуса, приращение Э. DS=SB-SA не зависит от пути интегрирования. Т. о., из второго начала термодинамики следует, что существует однозначная ф-ция состояния S, к-рая при квазистатич. адиабатич. процессах (dQ=0) остаётся постоянной. Процессы, в к-рых Э. остаётся постоянной, наз. изоэнтропийными. Примером может служить процесс, широко используемый для получения низких темп-р,— адиабатич. размагничивание (см. МАГНИТНОЕ ОХЛАЖДЕНИЕ). При изотермич. процессах изменение Э. равно отношению сообщённой системе теплоты к абс. темпре. Напр., изменение Э. при испарении жидкости равно отношению теплоты испарения к темп-ре испарения при условии равновесия жидкости с её насыщ. паром.Согласно первому началу термодинамики, dQ=dU+pdV, т. е. сообщаемое системе кол-во теплоты равно сумме приращения внутренней энергии dU и совершаемой системой элем. работы pdV, где р — давление, V -объём системы. С учётом первого начала термодинамики дифф. определение Э. принимает вид:dS =1/T(dU+pdV), (3)откуда следует, что Э. представляет собой потенциал термодинамический при выборе в кач-ве независимых переменных внутр. энергии U и объёма V. Частные производные Э. связаны с Т и р соотношениями:1/T=(дS/дU (4) и p/T-=(дS/дV)U (5) к-рые определяют уравнения состояния системы (первое — калорическое, второе — термическое). Ур-ние (4) лежит в основе определения абсолютной температуры (см. ТЕМПЕРАТУРА, ТЕМПЕРАТУРНЫЕ ШКАЛЫ).Ф-ла (2) определяет Э. лишь с точностью до аддитивной постоянной (т. е. оставляет начало отсчёта Э. произвольным). Абс. значение Э. можно установить с помощью третьего начала термодинамики, основываясь на к-ром, за нач. точку отсчёта Э. принимают S0=0 при Т=0.Важность понятия Э. для анализа необратимых (неравновесных) процессов также была показана впервые Клаузиусом. Для необратимых процессов интеграл от приведённой теплоты dQ/T по замкнутому пути всегда отрицателен.
=0 — т. н. равенство Клаузиуса). Это равенство, эквивалентное второму началу термодинамики для равновесных процессов, Клаузиус получил, рассматривая произвольный циклич. процесс как сумму очень большого (в пределе бесконечно большого) числа элементарных Карно циклов. Математически равенство Клаузиуса необходимо и достаточно для того, чтобы выражениеdS=dQ/T (1)представляло собой полный дифференциал ф-ции состояния S, назв. «Э.» (дифф. определение Э.). Разность Э. системы в двух произвольных состояниях А и В (заданных, напр., значениями темп-р и объёмов) равна:SB-SA=?BAdQ/T (2)(интегр. определение Э.). Интегрирование здесь ведётся вдоль пути любого квазистатич. процесса, связывающего состояния А и В, при этом, согласно равенству Клаузиуса, приращение Э. DS=SB-SA не зависит от пути интегрирования. Т. о., из второго начала термодинамики следует, что существует однозначная ф-ция состояния S, к-рая при квазистатич. адиабатич. процессах (dQ=0) остаётся постоянной. Процессы, в к-рых Э. остаётся постоянной, наз. изоэнтропийными. Примером может служить процесс, широко используемый для получения низких темп-р,— адиабатич. размагничивание (см. МАГНИТНОЕ ОХЛАЖДЕНИЕ). При изотермич. процессах изменение Э. равно отношению сообщённой системе теплоты к абс. темпре. Напр., изменение Э. при испарении жидкости равно отношению теплоты испарения к темп-ре испарения при условии равновесия жидкости с её насыщ. паром.Согласно первому началу термодинамики, dQ=dU+pdV, т. е. сообщаемое системе кол-во теплоты равно сумме приращения внутренней энергии dU и совершаемой системой элем. работы pdV, где р — давление, V -объём системы. С учётом первого начала термодинамики дифф. определение Э. принимает вид:dS =1/T(dU+pdV), (3)откуда следует, что Э. представляет собой потенциал термодинамический при выборе в кач-ве независимых переменных внутр. энергии U и объёма V. Частные производные Э. связаны с Т и р соотношениями:1/T=(дS/дU (4) и p/T-=(дS/дV)U (5) к-рые определяют уравнения состояния системы (первое — калорическое, второе — термическое). Ур-ние (4) лежит в основе определения абсолютной температуры (см. ТЕМПЕРАТУРА, ТЕМПЕРАТУРНЫЕ ШКАЛЫ).Ф-ла (2) определяет Э. лишь с точностью до аддитивной постоянной (т. е. оставляет начало отсчёта Э. произвольным). Абс. значение Э. можно установить с помощью третьего начала термодинамики, основываясь на к-ром, за нач. точку отсчёта Э. принимают S0=0 при Т=0.Важность понятия Э. для анализа необратимых (неравновесных) процессов также была показана впервые Клаузиусом. Для необратимых процессов интеграл от приведённой теплоты dQ/T по замкнутому пути всегда отрицателен.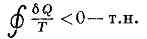 Клаузиуса неравенство. Это неравенство — следствие теоремы Карно: кпд частично или полностью необратимого циклич. процесса всегда меньше, чем кпд обратимого цикла. Из неравенства Клаузиуса вытекает, что
Клаузиуса неравенство. Это неравенство — следствие теоремы Карно: кпд частично или полностью необратимого циклич. процесса всегда меньше, чем кпд обратимого цикла. Из неравенства Клаузиуса вытекает, что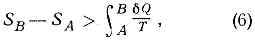 поэтому Э. адиабатически изолированной системы при необратимых процессах может только возрастать.Т. о., О. определяет хар-р процессов в адиабатич. условиях: возможны только такие процессы, при к-рых Э. либо остаётся неизменной (обратимые процессы), либо возрастает (необратимые процессы). При этом не обязательно, чтобы возрастала Э. каждого из тел, участвующих в процессе. Увеличивается общая сумма Э. тел, в к-рых процесс вызвал изменения.Термодинамич. равновесию адиабатич. системы соответствует состояние с максимумом Э. Энтропия может иметь не один, а неск. максимумов, при этом система будет иметь неск. состояний равновесия. Равновесие, к-рому соответствует наибольший максимум Э., наз. абсолютно устойчивым (стабильным). Из условия максимальности Э. адиабатич. системы в состоянии равновесия вытекает важное следствие: темп-ра всех частей системы в состоянии равновесия одинакова.Понятие Э. применимо и к термодинамически неравновесным состояниям, если отклонения от термодинамики равновесия невелики и можно ввести представление о локальном термодинамическом равновесии в малых, но ещё макроскопич. объёмах. В целом Э. неравновесной системы равна сумме Э. её частей, находящихся в локальном равновесии.Термодинамика неравновесных процессов позволяет более детально исследовать процесс возрастания Э. и вычислить кол-во Э., образующейся в ед. объёма в ед. времени вследствие отклонения от термодинамич. равновесия,— производство энтропии.Статистич. физика связывает Э. с вероятностью осуществления данного макроскопич. состояния системы. Э. определяется через логарифм статистического веса W данного равновесного состояния:S=klnW(?, N), (7)где W(?, N)—число квантовомеханич. уровней в узком интервале энергии D? вблизи значения энергии ? системы из N ч-ц, в классич. статистич. физике W — величина объёма в фазовом пространстве системы при заданных ? и N. Впервые связь Э. с вероятностью состояния системы была установлена австр. физиком Л. Больцманом в 1872: возрастание Э. системы обусловлено её переходом из менее вероятного состояния в более вероятное. Иными словами, эволюция замкнутой системы осуществляется в направлении наиболее вероятного распределения энергии по отд. подсистемам.В отличие от термодинамики, статистич. физика рассматривает особый класс процессов — флуктуации, при к-рых система переходит из более вероятного состояния в менее вероятное, и её Э. уменьшается. Наличие флуктуации показывает, что закон возрастания Э. выполняется только в ср. для большого промежутка времени.Э. в статистич. физике тесно связана с информац. Э., к-рая служит мерой неопределённости сообщений (сообщения описываются множеством величин x1, х2, . . ., хn и вероятностей Р1, Р2,. . .,Рn появления этих величин в сообщении). Для определённого (дискретного) статистич. распределения вероятностей Рk информац. Э. называют величинуHи=-Snk=1РkInPk при Snk=1Pk=1.(8)Ни=0, если к.-л. из Рk равно 1, а ост.— нулю, т. е. информация достоверна, неопределённость отсутствует. Э. принимает наибольшее значение, когда все Pk одинаковы (неопределённость в информации максимальна). Информац. Э., как и термодинамическая, обладает св-вом аддитивности (Э. неск. сообщений равна сумме Э. отд. сообщений). Из вероятностной трактовки информац. Э. могут быть выведены осн. распределения статистич. физики: каноническое Гиббса распределение, к-рое соответствует макс. значению информац. Э. при заданной ср. энергии, и большое канонич. распределение Гиббса — при заданных ср. энергии и числе ч-ц в системе.
поэтому Э. адиабатически изолированной системы при необратимых процессах может только возрастать.Т. о., О. определяет хар-р процессов в адиабатич. условиях: возможны только такие процессы, при к-рых Э. либо остаётся неизменной (обратимые процессы), либо возрастает (необратимые процессы). При этом не обязательно, чтобы возрастала Э. каждого из тел, участвующих в процессе. Увеличивается общая сумма Э. тел, в к-рых процесс вызвал изменения.Термодинамич. равновесию адиабатич. системы соответствует состояние с максимумом Э. Энтропия может иметь не один, а неск. максимумов, при этом система будет иметь неск. состояний равновесия. Равновесие, к-рому соответствует наибольший максимум Э., наз. абсолютно устойчивым (стабильным). Из условия максимальности Э. адиабатич. системы в состоянии равновесия вытекает важное следствие: темп-ра всех частей системы в состоянии равновесия одинакова.Понятие Э. применимо и к термодинамически неравновесным состояниям, если отклонения от термодинамики равновесия невелики и можно ввести представление о локальном термодинамическом равновесии в малых, но ещё макроскопич. объёмах. В целом Э. неравновесной системы равна сумме Э. её частей, находящихся в локальном равновесии.Термодинамика неравновесных процессов позволяет более детально исследовать процесс возрастания Э. и вычислить кол-во Э., образующейся в ед. объёма в ед. времени вследствие отклонения от термодинамич. равновесия,— производство энтропии.Статистич. физика связывает Э. с вероятностью осуществления данного макроскопич. состояния системы. Э. определяется через логарифм статистического веса W данного равновесного состояния:S=klnW(?, N), (7)где W(?, N)—число квантовомеханич. уровней в узком интервале энергии D? вблизи значения энергии ? системы из N ч-ц, в классич. статистич. физике W — величина объёма в фазовом пространстве системы при заданных ? и N. Впервые связь Э. с вероятностью состояния системы была установлена австр. физиком Л. Больцманом в 1872: возрастание Э. системы обусловлено её переходом из менее вероятного состояния в более вероятное. Иными словами, эволюция замкнутой системы осуществляется в направлении наиболее вероятного распределения энергии по отд. подсистемам.В отличие от термодинамики, статистич. физика рассматривает особый класс процессов — флуктуации, при к-рых система переходит из более вероятного состояния в менее вероятное, и её Э. уменьшается. Наличие флуктуации показывает, что закон возрастания Э. выполняется только в ср. для большого промежутка времени.Э. в статистич. физике тесно связана с информац. Э., к-рая служит мерой неопределённости сообщений (сообщения описываются множеством величин x1, х2, . . ., хn и вероятностей Р1, Р2,. . .,Рn появления этих величин в сообщении). Для определённого (дискретного) статистич. распределения вероятностей Рk информац. Э. называют величинуHи=-Snk=1РkInPk при Snk=1Pk=1.(8)Ни=0, если к.-л. из Рk равно 1, а ост.— нулю, т. е. информация достоверна, неопределённость отсутствует. Э. принимает наибольшее значение, когда все Pk одинаковы (неопределённость в информации максимальна). Информац. Э., как и термодинамическая, обладает св-вом аддитивности (Э. неск. сообщений равна сумме Э. отд. сообщений). Из вероятностной трактовки информац. Э. могут быть выведены осн. распределения статистич. физики: каноническое Гиббса распределение, к-рое соответствует макс. значению информац. Э. при заданной ср. энергии, и большое канонич. распределение Гиббса — при заданных ср. энергии и числе ч-ц в системе.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- ЭНТРОПИЯ
-
(от греч. entropia-поворот, превращение)- понятие, впервые введённое в термодинамике для определения меры необратимого рассеяния энергии. В статистической физике Э. служит мерой вероятности осуществления к.-л. макроскопич. состояния, в теории информации- мерой неопределённости к.-л. опыта (испытания), к-рый может иметь разл. исходы. Эти трактовки Э. имеют глубокую внутр. связь. Напр., на основе представлений об информационной энтропии можно вывести все равновесные статистич. распределения (см. Гиббса распределения).
Энтропия в термодинамике была введена Р. Клаузиусом (R. Clausius, 1865) на основе второго начала термодинамики, к-рое можно сформулировать математически в виде Клаузиуса неравенства
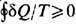 . Интеграл берётся по замкнутому циклич. процессу, при к-ром система получает (или у неё отбирают) малые количества теплоты dQ при соответствующих значениях абс. темп-ры Т. Знак равенства относится к обратимым процессам (р а в е н с т в о К л а у з и у с а). Из равенства Клаузиуса следует, что для обратимого процесса
. Интеграл берётся по замкнутому циклич. процессу, при к-ром система получает (или у неё отбирают) малые количества теплоты dQ при соответствующих значениях абс. темп-ры Т. Знак равенства относится к обратимым процессам (р а в е н с т в о К л а у з и у с а). Из равенства Клаузиуса следует, что для обратимого процесса

есть полный дифференциал ф-ции состояния S, называемый Э. (дифференциальное определение Э.). Разность Э. системы в двух произвольных состояниях А и В (заданных, напр., значениями темп-р и объёмов) равна
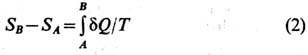
(интегральное определение Э.). Интегрирование здесь ведётся вдоль пути любого квазистатич. обратимого процесса, связывающего состояния А и В. Т. о., из второго начала термодинамики следует, что существует однозначная ф-ция состояния S, к-рая при обратимых адиабатич. процессах (dQ =0) остаётся постоянной. Из неравенства Клаузиуса вытекает, что при необратимых процессах
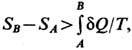
поэтому в адиабатически изолированных системах (см. Термодинамическая система )при необратимых процессах Э. может только возрастать (закон возрастания Э.).
Согласно первому началу термодинамики,
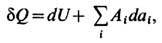
т. е. сообщаемое системе кол-во теплоты равно сумме приращения внутренней энергии dU и совершаемой системой элементарной работы, где а i - внеш. параметры состояния, Ai - сопряжённые им внутр. параметры. Когда единственным внеш. параметром является объём системы V, элементарная работа равна pdV, где р- давление. С учётом первого начала термодинамики дифференциальное определение Э. принимает вид
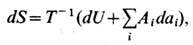
откуда следует, что Э. представляет собой потенциал термодинамический при выборе в качестве независимых переменных внутр. энергии U и внеш. параметров а i . Частные производные Э.

определяют уравнения состояния системы. Уравнение (3) определяет абсолютную температурную шкалу.
Ф-ла (2) определяет Э. лишь с точностью до аддитивной постоянной (т. е. оставляет начало отсчёта Э. произвольным). Абс. значение Э. можно установить с помощью третьего начала термодинамики, согласно к-рому принимается S= 0 при Т=0.
Энтропия в неравновесной термодинамике может быть определена для таких неравновесных состояний, когда можно ввести представление о локальном равновесии термодинамическом в отд. подсистемах (напр., в малых, но мак-роскопич. объёмах). По определению, Э. неравновесной системы равна сумме Э. её частей, находящихся в локальном равновесии. Термодинамика неравновесных процессов позволяет более детально исследовать процесс возрастания Э. и вычислить кол-во Э., образующееся в единице объёма в единицу времени вследствие отклонения от тер-модинамич. равновесия - производство энтропии. Для пространственно неоднородных неравновесных систем второе начало термодинамики может быть записано в виде у р а в н е н и я б а л а н с а д л я п л о т н о с т и
э н т р о п и и S(x, t), где х - радиус-вектор физически бесконечно малого элемента среды:
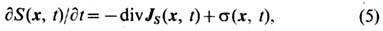
JS(x, t) - вектор потока Э.; s(x,t)>=0-л о к а л ь н о е п р ои з в о д с т в о э н т р о п и и. Полное производство Э. равно интегралу от s( х, t )по объёму системы. Если т е р м о д ин а м и ч. с и л ы Xi(x, t )(градиенты темп-ры, хим. потенциалов компонентов, массовой скорости и т. д.) создают в системе сопряжённые им потоки Ji (x, t )(теплоты, вещества, импульса и др.), то в такой системе
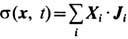 . Если величины Xi , Ji - векторы или тензоры, то в выражении для s подразумевается их полная свёртка. Потоки Ji связаны с термодинамич. силами Xk линейными соотношениями
. Если величины Xi , Ji - векторы или тензоры, то в выражении для s подразумевается их полная свёртка. Потоки Ji связаны с термодинамич. силами Xk линейными соотношениями 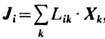 , где Lik- онсагеровские кинетические коэффициенты. Следовательно, локальное производство Э.
, где Lik- онсагеровские кинетические коэффициенты. Следовательно, локальное производство Э. 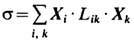 выражается квадратичной формой от термодинамич. сил.
выражается квадратичной формой от термодинамич. сил.
Энтропия в равновесной статистической физике зависит от выбора статистич. ансамбля. Для микроканонич. ансамбля Гиббса (см. Гиббса распределения), описывающего равновесное состояние изолированных систем, Э. выражается через статистический вес состояния W(
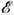 , N, V):
, N, V):
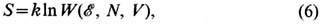
где W(
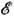 , N, V) - число квантовомеханич. состояний, энергия к-рых
, N, V) - число квантовомеханич. состояний, энергия к-рых 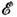 лежит в узком интервале
лежит в узком интервале 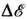 вблизи значения
вблизи значения 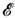 системы из N частиц в объёме V. В классич. статистич. физике W- величина безразмерного объёма в фазовом пространстве системы при заданных
системы из N частиц в объёме V. В классич. статистич. физике W- величина безразмерного объёма в фазовом пространстве системы при заданных 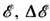 , N, V:
, N, V:
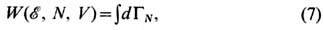
где d Г N = dpdq/N!h3N; dpdq - элемент объёма в 6N -мерном фазовом пространстве системы из N частиц ( р - обобщённый импульс; q - обобщённая координата). Интегрирование ведётся в пределах
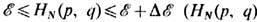 - Гамильтона функция системы из N частиц). Для канонич. ансамбля Гиббса, описывающего равновесное состояние систем в термостате, Э. выражается через каноническое распределение Гиббса f(p, q):
- Гамильтона функция системы из N частиц). Для канонич. ансамбля Гиббса, описывающего равновесное состояние систем в термостате, Э. выражается через каноническое распределение Гиббса f(p, q):
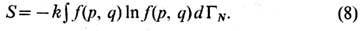
Аналогичным образом определяется Э. для систем с переменным числом частиц в термостате через большое каноническое распределение Гиббса fN(p, q):
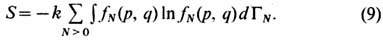
В квантовой статистике Э. для всех равновесных ансамблей выражается через статистич. оператор (или матрицу плотности)
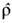 :
:

Символ Sp
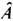 означает сумму диагональных матричных элементов оператора
означает сумму диагональных матричных элементов оператора 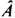 ; суммирование ведётся по волновым ф-циям состояний допустимой симметрии относительно перестановки частиц.
; суммирование ведётся по волновым ф-циям состояний допустимой симметрии относительно перестановки частиц.
Вдали от областей сосуществования фаз и критич. точек значения Э., вычисленные с помощью разл. ансамблей Гиббса, совпадают с термодинамич. Э. в пределе N
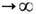 , V
, V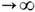 . при N/V=const (см. Термодинамический предел).
. при N/V=const (см. Термодинамический предел).
Информационная энтропия. Э. в статистич. физике связана с информационной Э., к-рая служит мерой неопределённости сообщений (сообщения описываются множеством величин х1 х2, ..., х n и вероятностей Р1,Р2,...,Р n их появления). Для дискретного статистич. распределения вероятностей Pk информационной Э. (с точностью до постоянного множителя) наз. величину
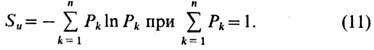
Величина Su =0, если к.-л. из Pk равна 1, а остальные - нулю, т. е. информация достоверна, неопределённость отсутствует. Э. принимает наибольшее значение, когда все Pk одинаковы (неопределённость в информации максимальна). Непрерывной случайной величине х сф-цией распределения f(x )соответствует информационная Э.
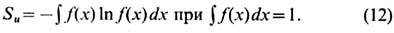
Информационная Э., как и термодинамическая, обладает свойством аддитивности (Э. неск. сообщений равна сумме Э. отд. сообщений). Из вероятностной трактовки Э. в статистич. физике выводятся осн. равновесные распределения: канонич. распределение Гиббса, к-рое соответствует макс. значению информационной Э. при заданной ср. энергии, и большое канонич. распределение Гиббса - при заданных ср. энергии и ср. числе частиц в системе.
Энтропия в неравновесной статистической физике зависит от способа описания неравновесного состояния системы. Напр., неравновесное гидродинамич. состояние од-нокомпонентных газов и жидкостей определяется неоднородными распределениями ср. значений плотностей энергии <
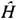 (x)>t, числа частиц <
(x)>t, числа частиц <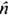 (x)>t и импульса <
(x)>t и импульса <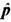 (x)>t, т. е. плотностей интегралов движения. Динамические переменные
(x)>t, т. е. плотностей интегралов движения. Динамические переменные 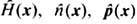 в классич. случае являются ф-циями координат и импульсов частиц, а в кван. случае-соответствующими операторами. Операция усреднения <...>t выполняется с н е р а в н о в е с н о й ф у н к ц и е й р а с п р е д е л е н и я f(p, q, t), удовлетворяющей Лиувилля уравнению дf/дt ={H, f}; Н - гамильтониан системы, {Н, f} - Пуассона скобка. В квантовом случае в уравнении Лиувилля надо заменить f на неравновесный статистич. оператор p^(t), а классич. скобку Пуассона - на квантовую.
в классич. случае являются ф-циями координат и импульсов частиц, а в кван. случае-соответствующими операторами. Операция усреднения <...>t выполняется с н е р а в н о в е с н о й ф у н к ц и е й р а с п р е д е л е н и я f(p, q, t), удовлетворяющей Лиувилля уравнению дf/дt ={H, f}; Н - гамильтониан системы, {Н, f} - Пуассона скобка. В квантовом случае в уравнении Лиувилля надо заменить f на неравновесный статистич. оператор p^(t), а классич. скобку Пуассона - на квантовую.
Э. в неравновесной статистич. физике пропорциональна (S = kSu )максимуму информационной Э. Su=-<ln f>t при заданных ср. значениях динамических переменных, выбранных для описания неравновесного состояния. Напр., если неравновесное состояние характеризуется ср. значениями
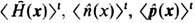 , то максимуму информац. Э. соответствует л о к а л ь н о-р а в н о в е с н о е р а с п р е д ел е н и е
, то максимуму информац. Э. соответствует л о к а л ь н о-р а в н о в е с н о е р а с п р е д ел е н и е
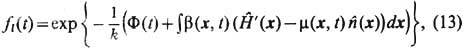
где
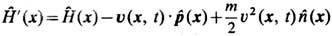 -плотность энергии в сопровождающей системе координат, движущейся с массовой скоростью u(x, t). Ф у н к ц и о н а л М а -с ь е - П л а н к а Ф(t) определяется из условия нормировки fl и зависит от b(x, t), b( х, t)m(x, t),u(x,t), где b(x, t) - обратная локальная темп-pa, m(x, t) - локальный хим. потенциал. В этом случае неравновесная Э.
-плотность энергии в сопровождающей системе координат, движущейся с массовой скоростью u(x, t). Ф у н к ц и о н а л М а -с ь е - П л а н к а Ф(t) определяется из условия нормировки fl и зависит от b(x, t), b( х, t)m(x, t),u(x,t), где b(x, t) - обратная локальная темп-pa, m(x, t) - локальный хим. потенциал. В этом случае неравновесная Э.
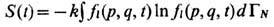
является функционалом
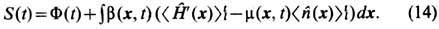
Операция <...>tl означает усреднение по распределению (13), причём
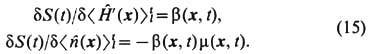
Основная идея неравновесной термодинамики состоит в том, что термодинамич. равенства должны выполняться для элемента среды, движущегося с массовой скоростью. Из (15) следует, что для этого необходимо, чтобы
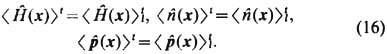
Равенства (16) являются условиями самосогласованного выбора параметров b(x, t),m(x,t), u(x, t )и определяют их зависимость от неравновесных ср. значений <H^(x)>t ,
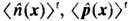 .
.
Локально-равновесное распределение служит вспомогательным распределением для определения понятия Э. неравновесного состояния, но не описывает необратимых переноса явлений. Потоки энергии и импульса, вычисленные с помощью fl (t), соответствуют потокам этих величин в идеальной гидродинамике. Неравновесная ф-ция распределения может быть получена как формальное решение ур-ния Лиувилля с нач. условием локального равновесия в нек-рый момент времени t0: f(t; t0) = exp [- iL(t - t0)] fl(t0). Оператор Лиувилля L определяется через скобки Пуассона: iLf= {H, f}. Это решение зависит от нач. состояния, к-рое реальная система должна "забывать" из-за корреляций между элементами среды. Можно считать, что пучок фазовых траекторий с различными t0(-
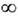 <t0<t )реализует ансамбль Гиббса для неравновесных состояний. Предполагая, что нач. состояния распределены с экспоненциальной вероятностью T-1 ехр[-(t - t0)/Т](г и п о т е з а о б а п р и о р н ы х в е р оя т н о с т я х), получим неравновесную ф-цию распределения
<t0<t )реализует ансамбль Гиббса для неравновесных состояний. Предполагая, что нач. состояния распределены с экспоненциальной вероятностью T-1 ехр[-(t - t0)/Т](г и п о т е з а о б а п р и о р н ы х в е р оя т н о с т я х), получим неравновесную ф-цию распределения
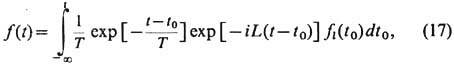
Т-1 =e
 +0 после термодинамич. предельного перехода при вычислении средних. Ф-ция распределения (17) удовлетворяет уравнению Лиувилля с малым источником в правой части e
+0 после термодинамич. предельного перехода при вычислении средних. Ф-ция распределения (17) удовлетворяет уравнению Лиувилля с малым источником в правой части e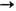 +0. Кроме того, предполагаются выполненными условия самосогласования (16).
+0. Кроме того, предполагаются выполненными условия самосогласования (16).
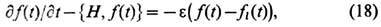
С помощью ф-ции распределения (17) можно усреднить уравнения движения для
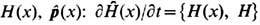 ,
, 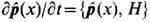 и получить теплопроводности уравнение и Навье - Стокса уравнение, в к-рых коэффициенты тепло-проводности и вязкости представлены в виде пространственно-временных корреляционных функций потоков энергии и импульса ( Грина-Кубо формулы). Отсюда следует уравнение баланса (5) для плотности Э. и другие соотношения неравновесной термодинамики.
и получить теплопроводности уравнение и Навье - Стокса уравнение, в к-рых коэффициенты тепло-проводности и вязкости представлены в виде пространственно-временных корреляционных функций потоков энергии и импульса ( Грина-Кубо формулы). Отсюда следует уравнение баланса (5) для плотности Э. и другие соотношения неравновесной термодинамики.
В неравновесной статистич. физике закон возрастания Э. тесно связан со свойством симметрии уравнения Лиувилля относительно обращения времени. Малый член ~e
 +0 в уравнении (18) нарушает эту симметрию, снимая вырождение, т. е. отбирая запаздывающее решение уравнения Лиувилля. Такое решение приводит к s>0 в уравнении (5), т. е. делает возможным возрастание Э. При этом существенно, что e
+0 в уравнении (18) нарушает эту симметрию, снимая вырождение, т. е. отбирая запаздывающее решение уравнения Лиувилля. Такое решение приводит к s>0 в уравнении (5), т. е. делает возможным возрастание Э. При этом существенно, что e +0 после термодинамич. предельного перехода. Другое решение уравнения Лиувилля (c e
+0 после термодинамич. предельного перехода. Другое решение уравнения Лиувилля (c e -0) приводит к убыванию Э. и должно быть отброшено как нефизическое.
-0) приводит к убыванию Э. и должно быть отброшено как нефизическое.
Э. для других процессов, отличных от гидродинамических, может быть определена с помощью к в а з и р а в н ов е с н о г о с о с т о я н и я, к-рое соответствует максимуму информационной Э. при заданных средних значениях не-к-рого набора динамических переменных, характеризующих неравновесное состояние. В общем случае квазиравновесное состояние может сильно отличаться от локального равновесия.
Понятие Э. используется также в классич. механике как характеристика хаоса динамического в системах с неустойчивостью движения-экспоненциальной расходимостью близких в нач. момент траекторий. Количественной мерой неустойчивости таких систем служит э н т р о п и я К р ыл о в а- К о л м о г о р о в а - С и н а я, или К- э н т р о п и я. Для широкого класса систем K -энтропия выражается через положительные показатели Ляпунова по формуле
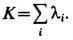
Если положительные показатели Ляпунова отсутствуют и, следовательно, движение устойчиво, то K -энтропия равна нулю.
Лит.: Майер Дж., Гепперт-Майер М., Статистическая механика, пер. с англ., 2 изд., М., 1980; де Гроот С., Мазур П., Неравновесная термодинамика, пер. с англ., М., 1964; Зубарев Д. Н., Неравновесная статистическая термодинамика, М., 1971; его же, Современные методы статистической теории неравновесных процессов, в кн.: Итоги науки и техники, сер. Современные проблемы математики, т. 15, М., 1980; Исихара А., Статистическая физика, пер. с англ., М., 1973; Ахиезер А. И., Пелет-минский С. В., Методы статистической физики, М., 1977; Гиббс Дж., Термодинамика. Статистическая механика, М., 1982; Леон-тович М. А., Введение в термодинамику. Статистическая физика, М., 1983; Климонтович Ю. Л., Статистическая теория открытых систем, М., 1995. Д. Н. Зубарев, В. Г. Морозов.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.