Akademik

СОЛИТОН

СОЛИТОН: структурно устойчивая уединённая волна в нелинейной диспергирующей среде. С. ведут себя подобно ч-цам: при вз-ствии между собой или с нек-рыми др. возмущениями С. не разрушаются, а расходятся вновь, сохраняя свою структуру неизменной. Структура С. поддерживается стационарной за счёт баланса между действием нелинейности среды (см. НЕЛИНЕЙНЫЕ СИСТЕМЫ) и дисперсии (см. ДИСПЕРСИЯ ВОЛН). Напр., в случае гравитац. волн на поверхности жидкости для достаточно длинной плоской волны (l->2pH, где Н — глубина водоёма) дисперсия отсутствует, волны распространяются с фазовой скоростью v=?(g(H+h)), где g— ускорение свободного падения, h — возвышение поверхности воды в данной точке профиля волны. Вершина волны движется быстрее её подножия (нелинейность), поэтому крутизна фронта волны растёт до тех пор, пока протяжённость фронта не станет соизмеримой с величиной 2pН, после чего скорость v будет зависеть от крутизны фронта (дисперсия). В результате на профиле волны появляются осцилляции (рис. 1), развитие к-рых приводит к образованию С.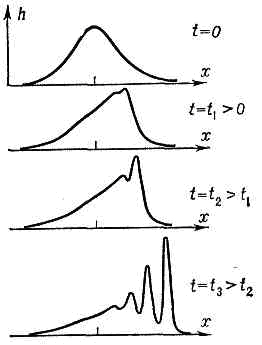

Рис. 1. Эволюция профиля волны на поверхности водоёма глубины Н.

С др. стороны, короткие волны (l-2pH) малой амплитуды обладают сильной дисперсией, т. к. их фазовая скорость v=?(gl/2p). Поэтому достаточно коротковолновое нач. возвышение расплывается, образуя осциллирующий цуг (подобно волне от брошенного в воду камня). Волны же с таким соотношением между l и амплитудой колебаний hмакc, что «обострение» фронта из-за нелинейности в точности компенсируется расплыванием из-за дисперсии, остаются стационарными, т. е. не изменяют своего профиля при распространении. Такая компенсация возможна в среде без притока и потерь энергии только для определ. класса волн, периодических или уединённых, т. е. С., к-рые чаще всего описываются решениями нелинейных дифф. ур-ний в обыкновенных производных.

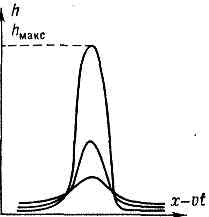Рис. 2. Форма солитонов разл. высоты h на поверхности воды; v — скорость распространения; t — время; х — координата

Нестационарные же волновые процессы, связанные с С., описываются нелинейными дифф. ур-ниями в частных производных. Наиболее детально изучено применительно к С. уравнение Кортевега — де Фриса, описывающее волны в средах с достаточно малыми нелинейностью и дисперсией, в частности С. на поверхности воды. Семейство С. небольшой высоты (hмакс-H) на поверхности воды (рис. 2) описывается выражением:

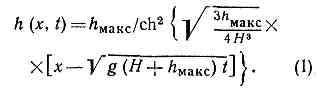С ростом hмакс растёт скорость С. v=?(g(H+hмакс)) и уменьшается его длина (пропорц. 1/hмакс). Аналогичный вид имеют С. др. природы, напр. ионнозвуковые и магнитозвуковые С. в плазме, С. внутренних гравитац. волн, С. в слоистой жидкости и т. д.

Рис. 3. Солитон в системе связанных маятников (вид сбоку).

В др. случаях, напр. в цепочке маятников, связанных пружинами, также существует движение в виде С. (рис. 3), описываемое выражением: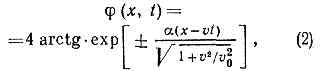

к-рое явл. решением т. н. синус-Гордона ур-ния. Здесь j — угол поворота маятника, a и v0 — постоянные, определяемые параметрами системы, v — скорость С. Такой С. представляет собой последоват. поворот маятников на 2p, причём знак плюс отвечает повороту по часовой стрелке, а минус — в противоположном направлении («антисолитон»). Характерная длина такого С. (число маятников, не находящихся в равновесии) тем больше, чем больше его скорость v. С., описываемые выражением (2), существуют в распределённых сверхпроводящих структурах (джозефсоновские переходы) и др.

Для ур-ний Кортевега — де Фриса, синус-Гордона и ряда др. ур-ний найдены решения, описывающие вз-ствие произвольного числа С., параметры к-рых не изменяются в результате вз-ствий, а также формирование С. в результате эволюции произвольного нач. импульса (рис. 1).

Впервые С. наблюдался в 1834 шотл. учёным Дж. С. Расселом в форме возвышения, бегущего по поверхности воды в канале. Теоретич. описание его было дано в 1895 голл. учёными Д. Кортевегом и Г. де Фрисом. В дальнейшем С. наблюдались в плазме, линиях передачи с ПП диодами и др. С., сближаясь, влияют друг на друга, т. к. в нелинейной среде не выполняется принцип суперпозиции. Тем не менее после вз-ствия С. не разрушаются, а расходятся вновь (рис. 4), сохраняя те же параметры, что и до вз-ствия,— как если бы столкнулись и разлетелись ч-цы, отсюда назв. «С.» (появилось в 1965, по аналогии с протоном и нейтроном, от лат. solus — один, уединённый).

Рис. 4. Вз-ствие двух бегущих в одном направлении солитонов вида (1) с близкими амплитудами.

Оказалось, что С. могут сохранять свою структуру длит. время при наличии небольшого затухания или в результате плавного искривления фронта волны в пр-ве (в частности, цилиндрич. и сферич. С.). С., как и ч-цы, могут образовывать связанные состояния из двух или более импульсов (рис. 5). В системе из многих С. это приводит, в частности, к появлению сложных стохастич. движений («газ. С.»).

Рис. 5. Связанная пара солитонов.

В системах с сильной дисперсией, если профиль стационарной волны близок к синусоидальному, также возможно существование модулир. волн в виде локализованных волн. пакетов со стационарно движущейся огибающей, к-рые также обнаруживают «частицеподобное» поведение при вз-ствии (С. «огибающей»). Такие С. возможны для волн на поверхности глубокого водоёма, ленгмюровских волн в плазме, мощных коротких (пикосекундных) световых импульсов в рабочей среде лазера и т. д.

С. играют важную роль в теории конденсир. состояния в-ва, в частности в квант. статистике, теории фазовых переходов. Солитонные решения имеют нек-рые ур-ния, предложенные для описания элем. ч-ц. Изучение св-в С. как «частицеподобных» волн, в т. ч. и возможных трёхмерных С., в к-рых поле убывает по всем направлениям в трёхмерном пр-ве (а не только по одной координате, как в приведённых выше примерах), привело к попыткам использовать С. при построении квант. нелинейной теории поля.

СОЛИТОН

(от лат. solus - один) - локализованное стационарноеили стационарное в среднем возмущение однородной или пространственно-периодич. нелинейной среды.

С. характеризуется следующими свойствами: локализован в конечной области;распространяется без деформации, перенося энергию, импульс, момент импульса;сохраняет свою структуру при взаимодействии с др. такими же С.; может образовыватьсвязанные состояния, ансамбли. Профиль (форма) С. определяется в нелинейнойсреде двумя конкурирующими процессами: расплыванием волны из-за дисперсиисреды и «опрокидыванием» нарастающего волнового фронта из-за нелинейности.

До нач. 1960-х гг. С. называли уединённую волну - волновой пакет неизменнойформы, распространяющийся с пост. скоростью по поверхности тяжёлой жидкостиконечной глубины и в плазме. Ныне под определение С. попадает множестворазнообразных физ. объектов. Первая классификация С. может быть сделанапо числу пространственных измерений, вдоль к-рых происходит локализациястационарного возмущения нелинейной среды. К одномерным С. относятся классич. уединённые волны в жидкостях, доменные стенки в ферро- и антиферромагнетиках,2p -импульсы и солитоны огибающей в нелинейной оптике (см. Солитоны оптические), локализов. моды коллективной проводимости в молекулахорганич. полупроводников и в одномерных металлах (см. Волны зарядовойплотности), С. (кванты магн. потока) в джозефсоновских контактах всверхпроводниках (см. Джозефсона эффект )и т. д. К двумерным С. относят дислокации в кристаллич. решётке, дисклинации в жидкихкристаллах, вихревые структуры в тонком слое сверхтекучей жидкости, особенно разнообразные в сверхтекучем Не ³ (см. Сверхтекучесть), магн. трубки (вихри Абрикосова) в сверхпроводниках 2-го рода (см. Сверхпроводимость), антициклональные области в геофиз. гидродинамике, в т. ч. «Большоекрасное пятно» на Юпитере, каналы самофокусировки в нелинейной оптике. Трёхмерные С.- это тороидальные вихревые структуры в ферромагнетиках итолстом слое сверхтекучего Не ³, солитонные модели элементарныхчастиц (см. Солитон в квантовой теории поля), чёрные дыры втеории гравитации. В квантовой теории поля рассматривают С., локализованныев четырёхмерном пространстве-времени,- инстантоны.

Математически С. представляют собой локализованные стационарные решениянелинейных дифференциальных уравнений в частных производных или их обобщений(дифференциально-разностных, интегро-дифференциальных и т. п. ур-ний).Во мн. случаях разл. физ. ситуации и явления описываются одними и темиже ур-ниями, напр. Кортевега - де Фриса уравнением, синус-Гордона уравнением, Шрёдингера уравнением нелинейным, Кадомцева- Петвиашвили уравнением. Линейные ур-ния (кроме одномерного волнового ур-ния) не имеют локализованныхстационарных решений. С. представляют собой существенно нелинейные объекты, поведение и свойства к-рых принципиально отличаются от поведения волновыхпакетов малой амплитуды. Различие особенно сильно, если С. обладает топологическимзарядом, т. е. если конфигурация волнового поля в присутствии С. топологическиотлична от конфигурации невозмущённого состояния. Значит. часть ур-ний, имеющих солитонные решения, принадлежит к классу ур-ний, в к-ром применим обратной задачи рассеяния метод, большинство из них являются интегрируемымигамильтоновыми системами.

Одномерные солитоны. Уединённая волна на поверхности жидкости конечнойглубины впервые наблюдалась в 1834 Дж. С. Расселлом (J. S. Russell). Матем. выражение для формы этой волны было получено в 1854 Ж. В. Буссинеском (J.V. Boussinesq):

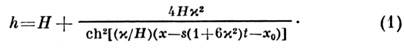
Здесь Н - невозмущённая глубина жидкости,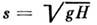- скорость длинных волн малой амплитуды, x₀ - положениецентра С.,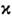В холодной замагниченной плазме и в плазме без магн. поля с горячими электронамитакже могут распространяться уединённые волны, аналогичные С. на поверхностижидкости (Р. 3. Сагдеев, 1957). С. были использованы Р. 3. Сагдеевым припостроении теории бесстолкновительных ударных волн в плазме, возникающих, напр., при обтекании Земли солнечным ветром.

Моделируя на ЭВМ поведение цепочки атомов, связанных нелинейными упругимисилами и описываемых ур-ниями движения

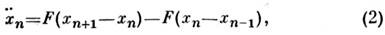
где 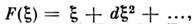л - номер атома в цепочке, Э. Ферми (Е. Fermi), Дж. Паста (J. Pasta) иС. Улам (S. Ulam) в 1954 обнаружили аномально медленную стохастизацию вэтой системе. Система не термализовалась (в ней не устанавливалось термодинамич. равновесие), а периодически возвращалась в исходное состояние с нач. распределением. При исследовании этой проблемы выяснилось, что в непрерывном пределе онапереходит в Кортевега - де Фриса ур-ние (КдФ)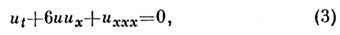

выведенное в 1895 для описания эволюции волнового пакета на поверхностижидхости малой глубины. Ур-ние КдФ является универсальным ур-нием, описывающимодномерные или квазиодномерные среды, в к-рых конкурируют слабая квадратичнаянелинейность [член 6 ии _х вур-нии (3)] и слабаялинейная дисперсия [член и _ххх^в ур-нии (3)].Оказалось, что оно описывает также и колебат. поведение цепочки атомов, а в пределе малой амплитуды и большой длины волны имеет солитонное решение:

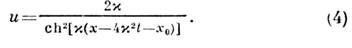
В зависимости от соотношения указанных выше двух факторов система переходитиз одного состояния в другое, а в случае их взаимной компенсации возникаетС.

Из численного решения ур-ния (3) [Н. Забуски (N. Zabusky) и М. Крускал(М. Kruskal), 1964] следует, что С. обладают значит. устойчивостью и пристолкновениях рассеиваются упруго, сохраняя свою форму и амплитуду. Анализируяэто явление, М. Крускал, Дж. Грин (G. Green), Ч. Гарднер (С. Gardner) иР. Миура (R. Miura) открыли в 1967 фундам. метод обратной задачи рассеяния, позволивший явно проинтегрировать ур-ние (3), к-рое можно представить какусловие совместности переопределённой системы линейных ур-ний для вспомогат. ф-ции :

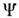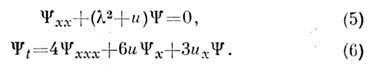
Ур-ние (5) представляет собой стационарное ур-ние Шрёдингера с потенциалом- u(x,t). Если потенциал удовлетворяет ур-нию КдФ (3), то дискретныесобств. значения ур-ния Шрёдингера не зависят от времени и непосредственносвязаны с С. Если ур-ние (5) имеет N дискретных собств. значений 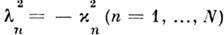, то при 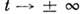будут присутствовать N С. вида (4) с параметрами 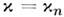.В общем случае в решении содержится также осциллирующая «несолитонная часть».Решение ур-ния (5), определённое методом обратной задачи рассеяния, имеетвид: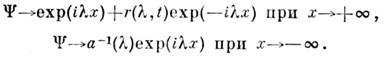

В чисто солитонном случае

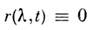
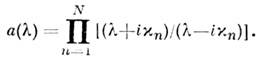
N-солитонное решение описывает рассеяние N С. друг на друге. Это рассеяние происходит упруго с сохранением амплитуд , сдвигаются лишьасимптотич. координаты С. При 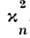парном столкновении С. с амплитудами 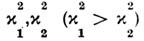С. приобретают сдвиги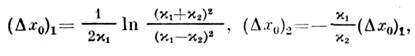

т. е. быстрый С. приобретает положительный, а медленный - отрицательныйсдвиги. При взаимодействии N С. полный сдвиг каждого С. равен алгебраич. сумме сдвигов от парных соударений, т. е. отсутствуют многосолитонные взаимодействия. Столкновения С., описываемых ур-ниями КдФ, можно наглядно представлятькак взаимодействие нерелятивистских частиц, между к-рыми действуют парныесилы отталкивания. Напр., для двух С. (4) с одинаковыми амплитудами 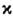,разделённых расстоянием L, много большим характерного размера С.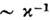, потенциал силы отталкивания

Типичная картина возникновения С. в океане, сфотографированная из космоса, изображенана рис.: чётко видны пять полос (солитонов), перемещающихся снизу справавверх налево.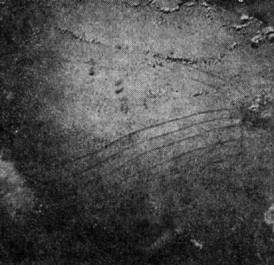

Шрёдингера нелинейное ур-ние для комплексной ф-ции u(x,t)

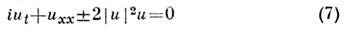
является одним из осн. ур-ний нелинейной физики, описывающим эволюциюоптич. волн в нелинейных кристаллах, ленгмюровских волн в плазме, тепловыхволн в твёрдых телах и др. При распространении одномерных квазигармонич. волн в слабонелинейных средах и результате кубичной нелинейности (член и _хх )и линейной дисперсии (член 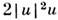) происходит самомодуляция - возникают волны огибающей. В случае равновесиянелинейного самосжатия и дисперсионного расплывания появляются С. огибающей. В случае знака «+» в ур-нии (7) С. огибающей имеет вид: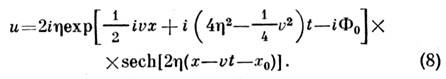

Здесь 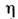и v - амплитуда и скорость С. [в отличие от С. (4), эти параметрыявляются взаимно независимыми], Ф ₀ и х₀ описывают фазу и положение С. в нач. момент.

В. Е. Захаров и А. Б. Шабат показали (1971), что ур-ние (7) также являетсяточно интегрируемым в рамках метода обратной задачи рассеяния с помощьювспомогат. переопределённой системы линейных ур-ний типа (5), (6) для многокомпонентной(векторной) ф-ции 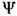. Следствием точной интегрируемости является наличие точных многосолитонныхрешений. Как и в случае ур-ния КдФ, эти решения описывают чисто упругиестолкновения С. с сохранением формы, амплитуды и скорости. Единств. следствиемстолкновения являются фазовые сдвиги - изменения параметров Ф ₀ и х ₀.

Одномерное ур-ние синус-Гордона. Точно интегрируемым с помощью вспомогат. линейных ур-ний типа (5), (6) для векторной ф-ции y является также синус-Гордонаур-ние

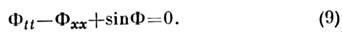
Это ур-ние встречается во мн. физ. задачах, в к-рых ангармонич. потенциалнелинейного самовоздействия волнового поля периодичен по полевой переменной Ф(х,t). Примерами являются длинные волны в джозефсоновских переходах, волны зарядовой плотности в одномерных металлах, нелинейные волнынамагниченности в легко плоскостных и слабых ферромагнетиках и т. д.

Ур-ние (9) имеет солитонные решения двух разл. типов: т. н. кинки ибризеры. К и н к

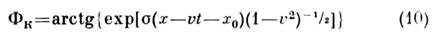
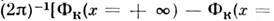
представляет собой уединённую волну, обладающую топологич. зарядом 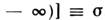, движущуюся со скоростью v (v² <1). Кинк имеет смыслт. н. флаксона - кванта магн. потока в теории длинных джозефсоновских переходов, доменной стенки - в ферромагнетиках, носителя заряда - в одномерных металлахи т. д. Точные решения ур-ния (9) описывают чисто упругие столкновениялюбого числа кинков (10), сопровождающиеся фазовыми сдвигами, т. е. изменениемпараметров x₀, характеризующих положение кинков в нач. момент. В частности, при столкновении двух кинков со скоростями v₁,v₂ (v₁v₂ )фазовыесдвиги равны: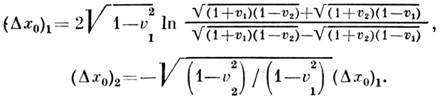

Видно, что фазовые сдвиги не зависят от топологич. зарядов кинков.

Как и для С., описываемых ур-ниями (3) и (7), полный фазовый сдвиг любогокинка при рассеянии на совокупности остальных кинков в точности равен суммесдвигов, порождённых его столкновениями с каждым из остальных кинков поотдельности.

Наглядно два кинка, разделённых расстоянием L, много большим их характерныхразмеров ~ (1 - v²)^-1/2, можно представлять как дверелятивистские частицы, взаимодействующие с потенциалом

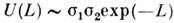
Т. о., кинки с одинаковыми зарядами 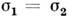отталкиваются, с противоположными 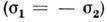- притягиваются.

Пара кинков с противоположным зарядом может образовать связанное осциллирующеесостояние - т. н. б р и з е р, представляющий собой 2-й тип точного солитонногорешения ур-ния (9):

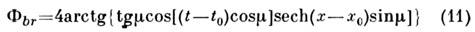
[движущийся бризер может быть получен из (11) преобразованием Лоренца].Параметр 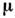,изменяющийся в пределах 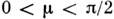, характеризует энергию связи 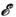бризера, определённую разность энергий пары удалённых покоящихся (v=0) кинков (10) и энергии бризера (11):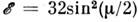. Столкновения бризеров друг с другом и с кинками также являются чистоупругими и сопровождаются аддитивными фазовыми сдвигами. В реальных системахбризер не наблюдается вследствие диссипации.

В пределе Ф ²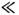1 подстановка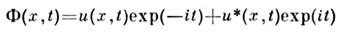

преобразует ур-ние (9) в нелинейное ур-ние Шрёдингера (7) (с верх. знаком).При этом бризер (11) (при 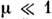) преобразуется в покоящийся С. (8) с амплитудой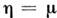

Многомерные солитоны. Двумерный С. является решением точно интегрируемогоур-ния Кадомцева - Петвиашвили

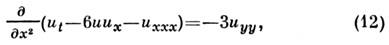
описывающего ионно-звуковые волны в плазме, капиллярные волны на поверхности«мелкой» жидкости и т. д. Точное решение ур-ния (12)

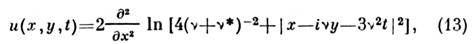
содержащее произвольный комплексный параметр v, описывает устойчивыйдвумерный С. (т. н. л а м п), движущийся со скоростью и = (v_x,Vy),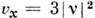,. При 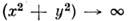решение. (13) убывает как ( х ² + y²)^-1,т. е., в отличие от одномерных С. (4), (8), (10), (11), характеризующихсяэкспоненциальным спадом профиля при ,двумерный С. (13) имеет степенную асимптотику. Столкновения любого числалампов (13) являются чисто упругими, причём, в отличие от одномерных С.,фазовые сдвиги тождественно равны нулю.

Понятие С. можно обобщить и на случай неинтегрируемых нелинейных волновыхур-ний. Сюда можно отнести почти интегрируемые с и с т е м ы, отличающиесяот универсальных интегрируемых ур-ний малыми возмущающими членами, чтоимеет место в реальных физ. системах. Теория возмущений для почти интегрируемыхсистем также основана на методе обратной задачи рассеяния [Д. Кауп (D.Каир), 1976; В. И. Карпман и Е. М. Маслов, 1977]. В почти интегрируемыхсистемах динамика С. более богата; в частности, малые возмущения могутпорождать неупругие взаимодействия С. и многосолитонные эффекты, отсутствующиев точно интегрируемом случае.

В системах, далёких от точно интегрируемых, взаимодействия С. оказываютсяглубоко неупругими. Так, неинтегрируемое релятивистски инвариантное волновоеур-ние

описывающее, напр., динамику параметра порядка при фазовых переходахтипа смещения в сегнетоэлектриках, имеет точное устойчивое решение типакинка:

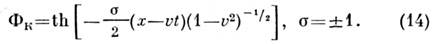
Численное исследование показывает, что столкновение двух кинков (14)с разл. топологич. зарядом 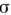может приводить к аннигиляции этих С. в квазилинейные волны (излучение).

Примером С. в неинтегрируемой трёхмерной системе является т. н. с ки р м и о н - солитон Скирма модели, хорошо описывающей низкоэнергетич. динамику нуклонов.

Нелинейное ур-ние Шрёдингера более общего вида, чем (7),

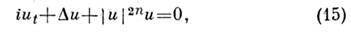
где - Лапласа оператор, действующий в пространстве произвольной размерности D, а н - произвольное положит, число, также может иметь солитонноерешение (это ур-ние интегрируемо лишь в случае п =1, D =1).Такой С. может быть устойчив лишь при nD< 2; в обратном случаеон оказывается неустойчивым относительно волнового коллапса (см.Солитон в плазме).

Лит.: Ребби К., Солитоны, пер. с англ., «УФН», 1980, т. 130,в. 2, с. 329; Теория солитонов. Метод обратной задачи, М., 1980; Солитоныв действии, под ред. К. Лонгрена, Э. Скотта, пер. с англ., М., 1981; Лэ м Д ж. Л., Введение в теорию солитонов, пер. с англ., М., 1983; Солитоны, под ред. Р. Буллафа, Ф. Кодри, пер. с англ., М., 1983; Косевич А. М., ИвановБ. А., Ковалев А. С., Нелинейные волны намагниченности. Динамические итопологические солитоны, К., 1983; Давыдов А. С., Солитоны в молекулярныхсистемах, К., 1984; Калоджеро Ф., Дегасперис А., Спектральные преобразованияи солитоны. Методы решения и исследования нелинейных эволюционных уравнений, пер. с англ., М., 1985; Раджараман Р., Солитоны и инстантоны в квантовойтеории поля, пер. с англ., М., 1985; Тахтаджян Л. А., Фаддеев Л. Д., Гамильтоновподход в теории солитонов, М., 1986; Абдуллаев Ф. X., Хабибуллаев П. К.,Динамика солитонов в неоднородных конденсированных средах, Таш., 1986;Филиппов А. Т., Многоликий солитон, М., 1986; Абловиц М. Д ж., С и г ур X., Солитоны и метод обратной задачи, пер. с англ., М., 1987; Solitons,ed. by S. E. Trullinger, V. E. Zakharov, V. L. Pokrovsky, Amst., 1986;К i v s h a r Y u. S., M a 1 о m e d B. A., Dynamics of solitons in nearlyintegrale systems, «Rev. Mod. Phys.», 1989, v. 61, р .763, В. Е. Захаров, Б. А. Маломед,

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.