Akademik

ПРОИЗВЕДЕНИЕ операторовв квантовой теории - запись произведения операторов в виде, когда все операторырождения стоят слева от всех операторов уничтожения. Н. п. возникает вметоде вторичного квантования, при этом предполагается, что любойоператор представим в виде полинома по операторам рождения и уничтожения. Отличит. свойство Н. п. - равенство нулю вакуумного среднего отлюбого оператора, записанного в виде Н. п. и не содержащего слагаемого, кратного единичному оператору. Н. п. было введено Дж. К. Виком (G. С. Wick)в 1950 для того, чтобы исключить из квантовой теории поля (КТП)формальные бесконечные величины типа энергии и заряда вакуумного состояния. Понятие Н. п. оказывается основным при решении многих фундам. вопросовКТП, таких, как вывод фейнмановской диаграммной техники (см. Фейнманадиаграммы), установление связи между операторным формализмом и формализмом функциональногоинтеграла, при построении аксиоматической квантовой теории поля ит. п.
Н. п. операторов А ₁,..., А _п обозначается символом : А ₁,..., А _п: Все свойства обычного произведения (линейностьи т. д.) остаются и для Н. п., к-рое, кроме того, обладает свойством перестановочностиоператоров под знаком Н. п., при этом операторы, подчиняющиеся Базе- Эйнштейна статистике, оказываются перестановочными, а подчиняющиеся Ферми- Дирака статистике - антиперестановочными.
Все динамич. величины, зависящие от операторовс одинаковыми аргументами (лагранжиан, тензор энергии-импульса, заряд ит. д.), во вторично-квантованной теории записываются в форме Н. п. Напр.,оператор числа частиц для свободного скалярного поля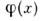 ,удовлетворяющего Клейна - Гордона уравнению, в терминах оператороврождения 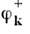и уничтожения 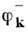частиц с импульсом k имеет вид

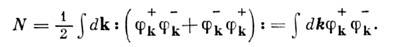Для вакуумного ср. оператора N получим (N)₀ =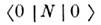=0, т. к.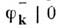N не был представлен в виде Н. п., то выражение вскобках, возникающее из принципа соответствия с классич. теорией (см. Соответствияпринцип), привело бы к (N)₀, пропорциональному расходящемусяинтегралу. Это типичный пример перестройки произведения в формализме Н. п. для операторов, подчиняющихся статистике Бозе - Эйнштейна. В случаефермионов выражение в скобках имеет вид (s- спиновая переменная),и для 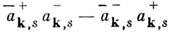полученияправильного оператора N, суммирующего все фермионные состояния, операторы рождения (а ⁺) и уничтожения (а ^-) фермионовдолжны антикоммутировать под знаком Н. п. (черта над оператором означаетдираковское сопряжение). Это - утверждение теоремы о связи спина и статистики( Паулитеорема), вытекающей пз принципа соответствия и формализма Н. п.
Для вычислений в квантовой теории полянеобходимо установить связь Н. п. с обычным произведением и хронологическимпроизведением. Эту связь устанавливают Вика теоремы. Определимспаривание двух линейных по операторам рождения и уничтожения операторов(соответственно хронологич. спаривание), обозначаемое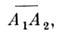 как вакуумное среднее от обычного произведения (хронологич. произведения).Спаривание даётся соответствующей перестановочной функцией. ДляН. п. двух линейных операторов получим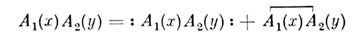

( х, у - точки пространства-времени).В общем случае справедлива след. теорема Вика: обычное (хронологическое)произведение п линейных операторов равно сумме Н. п. со всеми возможнымиспариваниями (хронологич. спариваниями), включая и Н. п. без спариваний. Линейность Н. п. гарантирует то, что спаривание выносится за знак Н. п.
При разложении действия в ряд теории возмущенийвозникает задача представить в виде Н. п. произведение операторов (напр.,лагранжианов взаимодействия), к-рые сами уже приведены к форме Н. п. Соответствующаятеорема Вика утверждает, что такое произведение равно сумме всех соответствующихН. п. со спариваниями, из числа к-рых исключены спаривания между линейнымиоператорами, находившимися в первонач. произведении под знаком одного Н. п.
Представляя процедуру нормального упорядоченияграфически, получим фейнмановскую диаграммную технику, сопоставив каждомуспариванию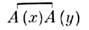 линию, соединяющую точки х и у. Найдём, напр., в квантовойэлектродинамике вакуумное среднее от произведения двух операторов электромагнитноготока: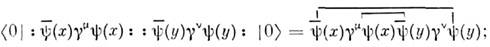

все остальные слагаемые дают нулевой вклад[здесь 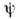- оператор спинорного поля,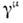( 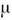= 0, 1, 2,3) - Дирака матрицы]. Графически последнее выражение даётсядиаграммой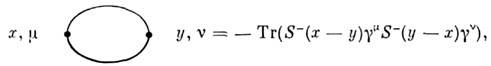

где S'(x - у) - перестановочнаяф-ция для поля электрона.

Понятие Н. п. позволяет установить связьмежду операторным формализмом и формализмом функционального интеграла. Для системы с одной степенью свободы каждому вектору Фока пространства 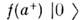ставится в соответствие аналитическая, функция f( а*) числовогоаргумента а* (* - знак комплексного сопряжения). Оператор уничтоженияв таком голоморфном представлении есть оператор дифференцирования по а*,а произвольному оператору А соответствует интегральный операторс ядром А( а*, а). Действие оператора А навектор f, скалярное произведение двух векторов, произведение операторов A₁ х _A2 описываются соответствующими свёртками с гауссовоймерой интегрирования: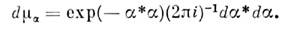

Для ядра произведения двух операторов имеем

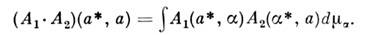
Поставим в соответствие оператору А, заданномуввиде Н. п.: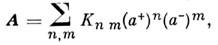функцию К(а*, а) = 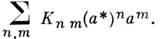Тогда ядро оператора А связано с К (а*, а )соотношением

А( а*, а) = ехр(а*а)К(а*, а).

Рассмотрим оператор эволюции 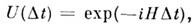где Н= :h(а⁺, а ^-):. Его ядро для малых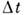

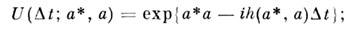
для конечного интервала 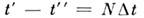следует взять свёртку N таких ядер. При этом из первого члена имеры интегрирования возникнет сумма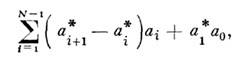

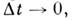
и после симметризации по а* = a_N и а = а ₀ в формальном пределе 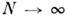получим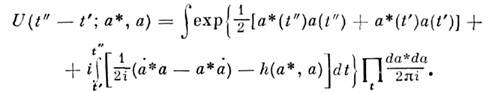

Это выражение и есть ф-ла для оператораэволюции, возникающая в методе функционального интеграла.

Лит.: Боголюбов Н. Н., Ширков Д. В., Введение в теорию квантованных полей, 4 изд., М., 1984; Березин Ф. А., Метод вторичного квантования, 2 изд., М., 1986; Славнов А. А., ФаддеевЛ. Д., Введение в квантовую теорию калибровочных полей, 2 изд., М., 1988:Боголюбов Н. Н., Ширков Д. В., Квантовые поля, 2 изд., М., 1990; ГлиммД., Джаффе А., Математические методы квантовой физики. Подход с использованиемфункциональных интегралов, пер. с англ., М., 1984.

Л. О. Чехов.