Akademik

(сверхтонкое расщепление) уровней энергии- расщепление уровней энергии атома, молекулы или кристалла на неск. подуровней, обусловленное взаимодействием магн. момента ядра с магн. полем, создаваемымгл. обр. электронами, а также взаимодействием квадрупольного момента ядрас неоднородным внутриатомным электрич. полем. Вследствие сверхтонкого расщепленияуровней в оптич. спектрах атомов и молекул вместо одной спектральной линиивозникает группа очень близких линий - С. с. спектральных линий.

Если ядро атома или одно из атомных ядер молекулы имеет спин I,то каждый подуровень С. с. характеризуется полным моментом F = J+7, где J - векторная сумма полного электронного момента и моментаорбитального движения ядер. Квантовые числа F полного момента пробегаютзначения F = |J - I|, |J - I| + 1,..., J+I(J и I- квантовые числа полного механич. электронного и ядерного спинового моментов).При 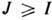числоподуровней равно 2I + 1, а при J < I оно равно 2J+ 1.Энергия подуровня записывается в виде: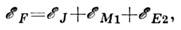

где 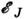- энергия уровня в пренебрежении С. с.,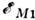- энергия магн. диполь-дипольного взаимодействия,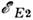- энергия электрич. квадрупольного взаимодействия.

В атомах и ионах осн. роль играет магн. взаимодействие, энергия к-рого

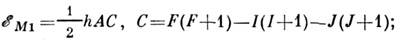
константа А (Гц) определяется усреднением по состоянию с полныммоментом F оператора магн. взаимодействия электронов с ядерным моментомВеличина взаимодействия пропорц. ядерному 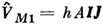магнетону 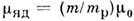' , где 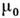- магнетон Бора, т - масса электрона и m _р - масса протона. Расстояние между подуровнями С. с. в атоме примерно в 1000 раз меньше, чем расстояние между компонентами тонкой структуры. Характерныевеличины сверхтонкого расщепления 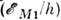для основного состояния атомов порядка одного или неск. ГГц. Сверхтонкоерасщепление возбуждённых уровней энергии убывает пропорц. энергии связивозбуждённого электрона в степени 3/2 и быстро уменьшается с увеличениеморбитального момента электрона. В случае водородрподобных атомов (Н, Не ⁺ и т. д.)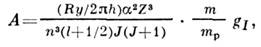

где 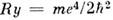- Ридберга постоянная,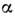- тонкой структуры постоянная, Z - заряд ядра (в единицах заряда электрона), п и l - главное и орбитальное квантовые числа, g_I- ядерный Ланде множитель. Электрич. квадрупольное взаимодействиесуществует при 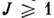для несферич. ядер с 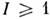.Оно даёт поправки к энергии подуровней атома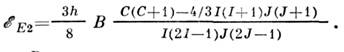

Константа В определяется усреднением по состоянию с полным моментомF оператора квадрупольного взаимодействия

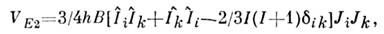
где i, k= 1, 2, 3,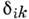- Кронекера символ. Обычно постоянная квадрупольного взаимодействия В на один-полтора порядка меньше константы А. Квадрупольноевзаимодействие приводит к нарушению правила интервалов Ланде.

Для дипольных переходов между подуровнями С. с. разных уровней выполняются отбора правила: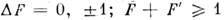. Между подуровнями С. с. одного уровня разрешены магн. дипольныепереходы с указанными выше правилами отбора, а также электрич.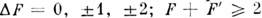квадрупольные переходы с правилами отбора.

Почти у всех молекул в основном электронном состоянии суммарный механич. момент электронов равен нулю и магн. С. с. колебательно-вращат. уровнейэнергии гл. обр. связана с вращением молекулы. В случае двухатомных, линейныхмногоатомных молекул и молекул типа симметричного волчка (см. Молекула), содержащих одно ядро со спином I на оси молекулы,

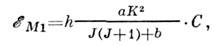
где J и К - квантовые числа полного вращат. момента и его проекциина ось волчка соответственно. Магн. расщепления составляют 1-100 кГц. Еслиспином обладают неск. ядер молекулы, то вследствие магн. взаимодействииядерных моментов возникают дополнит. расщепления порядка неск. кГц. МагнитнаяС. с. уровней энергии молекул, обладающих электронным моментом, того жепорядка, что и для атомов.

Если молекула в еостоянии 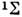содержит на своей оси ядро с 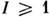, гл. роль играет квадрупольное расщепление: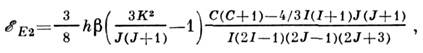

где 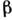(Гц) - константа, характерная для уровня с данными К и J.Величины квадрупольных расщеплений составляют десятки и сотни МГц.

В растворах, стёклах и кристаллах С. с. могут, напр., иметь уровни энергиипримесных ионов, свободных радикалов, электронов, локализованных на дефектахрешётки.

С. с. изучается методами магн. резонанса, др. методами радиоспектроскопии. Для возбуждённых состояний используют методы двойного резонанса (оптический- радиочастотный, инфракрасный - радиочастотный резонансы), а также методынелинейной лазерной спектроскопии.

Разл. изотопы хим. элементов обладают разл. значениями ядерного спина, а их линии испытывают изотопич. сдвиг. Поэтому часто происходит наложениеспектров разных изотопов и С. с. спектральных линий дополнительно усложняется.

Лит.: Таунс Ч., Шавлов А., Радиоспектроскопия, пер. с англ.,М., 1959; Собельман И. И., Введение в теорию атомных спектров, [2 изд.],М., 1977; Armstrong L. jr., Theory of the hyperfine structure of free atoms,N. Y.- [a. o.], 1971; P а д ц и г А. А., С М и р н о в Б. М., Параметрыатомов и атомных ионов. Справочник, 2 изд., М., 1986. Е. А. Юков.