Akademik

РЕНТГЕНОВСКИЙ СТРУКТУРНЫЙ АНАЛИЗ

РЕНТГЕНОВСКИЙ СТРУКТУРНЫЙ АНАЛИЗ: методы исследования структуры в-ва по распределению в пр-ве и интенсивностям рассеянного на анализируемом объекте рентгеновского излучения. Р. с. а. наряду с нейтронографией и электронографией явл. дифракц. структурным методом; в его основе лежит вз-ствие рентг. излучения с эл-нами в-ва, в результате к-рого возникает дифракция рентгеновских лучей. Дифракц. картина зависит от дл. волны используемого излучения и ат. строения объекта. Для исследования ат. структуры применяют излучение с дл. волны =1? (=0,1 нм), т. е. порядка размеров атомов. Методами Р. с. а. изучают металлы, сплавы, минералы, неорганич. и органич. соединения, полимеры, аморфные материалы, жидкости и газы, молекулы белков, нуклеиновых к-т и т. д. Наиболее успешно Р. с. а. применяют для установления ат. структуры крист. тел, т. к. кристаллы обладают строгой периодичностью строения и представляют собой созданную самой природой дифракционную решётку для рентг. излучения.

Историческая справка. Дифракция рентг. лучей на кристаллах открыта в 1912 нем. физиком М. Лауэ и его сотрудниками В. Фридрихом и П. Книппингом. Разработанная Лауэ теория дифракции рентг. лучей на кристаллах позволила связать l излучения, параметры элем. ячейки кристалла а, b, с (см. КРИСТАЛЛИЧЕСКАЯ РЕШЁТКА), углы падающего (a0, b0, g0) и дифракционного (a, b, g) лучей соотношениями:

а (cosa-cosa0)=hl,

b(cosb-cosb0)=kl, (1)

с(cosg-cosg0)=ll,

где h, k, l — целые числа (индексы кристаллографические). Ур-ния (1) наз. условием Лауэ для возникновения дифракции рентг. лучей, они требуют, чтобы разность хода между параллельными лучами, рассеянными атомами, отвечающими соседним узлам решётки, была равна целому числу l.

В 1913 англ. физик У. Л. Брэгг и одновременно с ним Г. В. Вульф показали, что дифракц. пучок можно рассматривать как отражение падающего луча от одной из систем кристаллографич. плоскостей (см. БРЭГГА — ВУЛЬФА УСЛОВИЕ). В том же году У. Г. и У. Л. Брэгги впервые исследовали ат. структуры простейших кристаллов рентг. дифракц. методами. В 1916 в Германии П. Дебай и П. Шерpep предложили дифракц. метод исследования структуры поликристаллич. материалов. В последующие годы были предложены разл. эксперим. методы изучения монокристаллов, развита теория дифракции и теория методов определения по эксперим. данным ат. структуры кристаллов, полимеров, аморфных тел и жидкостей, а также газов. В 50-х гг. начали бурно развиваться методы Р. с. а. с использованием ЭВМ в технике эксперимента и при обработке рентг. дифракц. информации.

Эксперим. методы Р. с. а. Для создания условий дифракции и регистрации излучения служат рентгеновские камеры, рентгеновские дифрактометры и рентгеновские гониометры. Рассеянное рентг. излучение в них фиксируется на фотоплёнке или измеряется детекторами ядерных излучений. В зависимости от состояния исследуемого образца и его св-в, а также от характера и объёма информации, к-рую необходимо получить, применяют разл. методы Р. с. а. Монокристаллы, отбираемые для исследования ат. структуры, должны иметь размеры =0,1 мм и по возможности обладать совершенной структурой. Исследованием дефектов в сравнительно крупных почти совершенных кристаллах занимается рентгеновская топография, к-рую иногда относят к Р. с. а.

Метод Лауэ — простейший метод получения рентгенограмм от монокристаллов. Кристалл в эксперименте Лауэ неподвижен, а используемое рентг. излучение имеет непрерывный спектр. Расположение дифракц. пятен на лауэграммах (см. рис. в ст. (см. ЛАУЭГРАММА)) зависит от симметрии кристалла и его ориентации относительно падающего луча, что позволяет установить его принадлежность к одной из 11 лауэвских групп симметрии и определять направление его кристаллографич. осей (ориентировать) с точностью до неск. угловых минут. По характеру пятен на лауэграммах, и особенно появлению астеризма, можно выявить внутр. напряжения и нек-рые др. дефекты кристаллич. структуры. Методом Лауэ проверяют качество монокристаллов при выборе образца для его более полного структурного исследования (см. ЛАУЭ МЕТОД).

М е т о д ы к а ч а н и я и в р а щ е н и я образца используют для определения периодов повторяемости (постоянной решётки) вдоль кристаллографич, направления в монокристалле. Они позволяют, в частности, установить параметры а, b, с элем. ячейки кристалла. В этом методе используют монохроматич. рентг. излучение, образец приводится в колебат. или вращат. движение вокруг оси, совпадающей с кристаллографич. направлением, вдоль к-рого и исследуют параметры а, b, с. Пятна на рентгенограммах качания и вращения, полученных в цилиндрич. кассетах, располагаются на семействе параллельных линий (рис. 1). Зная расстояние между этими линиями, l и диаметр кассеты можно вычислить искомые параметры кристалла. Условия (1) для дифракц. лучей в этом методе выполняются за счёт изменения углов при качании или вращении образца.

Р е н т г е н г о н и о м е т р и ч е с к и е м е т о д ы. Для полного исследования структуры монокристалла методами Р. с. а. необходимо не только установить положение, но и измерить интенсивности как можно большего числа дифракц. отражений, к-рые могут быть получены от кристалла при данной l и всех возможных ориентациях образца. Интенсивность определяют фотографически, измеряя микрофотометром степень почернения каждого пятна на рентгенограмме, или регистрируют непосредственно с помощью счётчиков рентг. квантов, что повышает чувствительность и точность измерений. Чтобы иметь полный набор отражений, в рентг. гониометрах получают серию рентгенограмм. На каждой из них фиксируются дифракц. отражения, на кристаллографич. индексы к-рых накладываются определ. ограничения (напр., на разных рентгенограммах регистрируются отражения типа hk0, hk1 и т. д., рис. 2).

Для установления ат. структуры ср. сложности (=50—100 атомов в элем. ячейке) необходимо измерить интенсивности неск. сотен и даже тысяч дифракц. отражений. Эту весьма трудоёмкую и кропотливую работу автоматич. микроденситометры и дифрактометры, управляемые ЭВМ, иногда выполняют в течение неск. недель (например, при анализе структур белков, когда число отражений =105).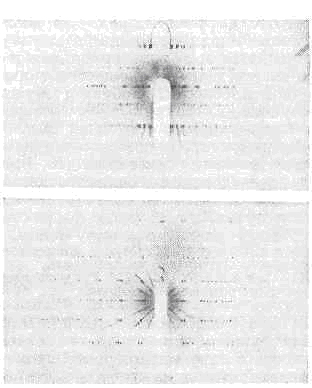

Рис. 1. Рентгенограммы минерала сейдозерита, полученные методами вращения (вверху) и качания (внизу) кристалла. Уменьшая угол качания, можно зафиксировать отд. отражения без перекрытия.

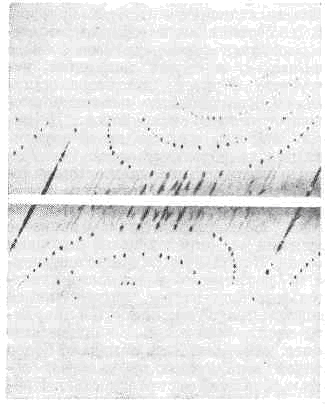Рис. 2. Рентгенограмма минерала сейдозерита, полученная в рентг. гониометре Вайсенберга. Зарегистрированные отражения имеют индексы hk0. Отражения, расположенные на одной кривой, характеризуются постоянными k.

Значительно сокращают время эксперимента многоканальные дифрактометры.

М е т о д и с с л е д о в а н и я п о л и к р и с т а л л о в (метод Дебая — Шеррера). Для исследования металлов, сплавов, крист. порошков, состоящих из множества мелких монокристаллов, используют монохроматич. излучение. Рентгенограмма поликристаллов (дебаеграмма) представляет собой неск. концентрич. колец, каждое из к-рых состоит из отражений от определённой системы плоскостей различно ориентированных кристаллов. Дебаеграммы разл. в-в имеют индивидуальный характер и позволяют идентифицировать соединения, определять фазовый состав образцов, размеры и преимуществ. ориентацию (текстурирование) зёрен в в-ве, осуществлять контроль за напряжениями в образце и др. (см. РЕНТГЕНОГРАФИЯ МАТЕРИАЛОВ, ДЕБАЯ — ШЕРРЕРА МЕТОД).

И с с л е д о в а н и е а м о р ф н ы х м а т е р и а л о в и ч а с т и ч н о у п о р я д о ч е н н ы х о б ъ е к т о в. Рентгенограмму с чёткими дифракц. максимумами можно получить только при полной трёхмерной периодичности образца. Чем ниже степень упорядоченности его ат. строения, тем более размытый, диффузный характер имеет рассеянное им рентг. излучение. Диаметр диффузного кольца на рентгенограмме аморфного в-ва (рис. 3) может служить для грубой оценки ср. межатомных расстояний в нём. С ростом степени упорядоченности (см. ДАЛЬНИЙ И БЛИЖНИЙ ПОРЯДОК) в строении объектов дифракц. картина усложняется (рис. 4) и, следовательно, содержит больше структурной информации.

Рис. 3. Рентгенограмма аморфного в-ва (ацетата целлюлозы).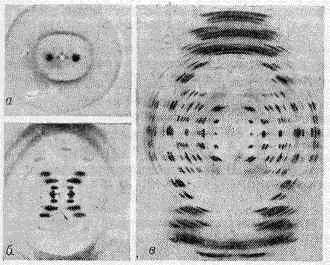

Рис. 4. Рентгенограммы биол. объектов: а — волоса; б — натриевой соли ДНК во влажном состоянии; в — текстуры натриевой соли ДНК.

М е т о д м а л о у г л о в о г о р а с с е я н и я позволяет изучать пространств. неоднородности в-ва, размеры к-рых превышают межатомные расстояния и составляют от 5—10 до =104 ?. Размеры неоднородностей в этом случае во много раз превышают длину волны используемого излучения, поэтому рассеянное рентг. излучение концентрируется вблизи первичного пучка — в области малых углов рассеяния. Распределение интенсивности в этой области отражает особенности структуры исследуемого объекта. Малоугловое рассеяние применяют для изучения пористых и мелкодисперсных материалов, сплавов и сложных биол. объектов. Для изолир. молекул белка и нуклеиновых к-т метод позволяет определять форму, размеры, мол. массу; в вирусах — характер взаимной укладки составляющих их компонент (белка, нуклеиновых к-т, липидов); в синтетич. полимерах — упаковку полимерных цепей; в порошках и сорбентах — распределение ч-ц и пор по размерам; в сплавах — возникновение и размеры фаз; в текстурах (в частности, в жидких кристаллах) — форму упаковки ч-ц (молекул) в различного рода надмолекулярные структуры. Рентг. малоугловой метод применяется и в пром-сти при контроле процессов изготовления катализаторов, высокодисперсных углей и т. д. В зависимости от строения объекта измерения производят для углов рассеяния от долей мин до нескольких град.

Определение ат. структуры по данным дифракции рентг, лучей. Расшифровка ат. структуры кристалла включает: установление размеров и формы его элем. ячейки; определение принадлежности кристалла к одной из 230 фёдоровских групп симметрии кристаллов; получение координат базисных атомов структуры. Первую и частично вторую задачи можно решить методами Лауэ и качания или вращения образца. Окончательно установить группу симметрии и координаты базисных атомов сложных структур возможно только с помощью сложного анализа и трудоёмкой матем. обработки значений интенсивностей всех дифракц. отражений от данного кристалла. Конечная цель — вычисление по эксперим. данным значений электронной плотности r(х, у, z) в любой точке ячейки кристалла с координатами х, у, z. Периодичность строения кристалла позволяет записать электронную плотность в нём через ряд Фурье:

r(х, у, z)=-1/VShklFhkl exp(-2pi(hx+ky+lz)), (2)

где V — объём элем. ячейки, Fhkl — коэфф. Фурье, к-рые в Р. с. а. наз. с т р у к т у р н ы м и а м п л и т у д а м и, i=?-1. Каждая структурная амплитуда характеризуется тремя целыми числами h, k, l и связана с тем дифракц. отражением, к-рое определяется условиями (1). Назначение суммирования (2) — математически собрать дифракц. рентг. отражения, чтобы получить изображение ат. структуры (производить синтез изображения т. о. приходится из-за отсутствия в природе линз для рентг. излучения).

Дифракц. отражение — волн. процесс. Он характеризуется амплитудой, равной ?Fhkl?, и фазой ahkl (сдвигом фазы отражённой волны по отношению к падающей), через к-рую выражается структурная амплитуда:

Fhkl=?Fhkl?(cosahkl+isinahkl).

Дифракц. эксперимент позволяет измерять только интенсивности отражений, пропорциональные ?Fhkl?2, но не их фазы. Определение фаз составляет осн. проблему расшифровки структуры кристалла, одинаковую в принципиальном отношении для кристаллов, состоящих и из атомов, и из молекул. Определив координаты атомов в молекулярном крист. в-ве, можно выделить его молекулы и установить их размер и форму.

Легко решается задача, обратная структурной расшифровке: матем. расчёт структурных амплитуд по известной ат. структуре, а по ним — интенсивностей дифракц. отражений. Метод проб и ошибок, исторически первый метод расшифровки структур, состоит в сопоставлении экспериментально полученных ?Fhkl?эксп с вычисленными на основе пробной модели значениями ?Fhkl?выч. В зависимости от величины фактора расходимости

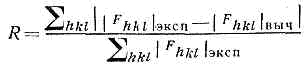пробная модель принимается или отвергается. Для некрист. объектов этот метод явл. практически единственным средством интерпретации дифракц. картины.

Другой путь к расшифровке ат. структур монокристаллов — применение т. н. ф-ций Патерсона (ф-ций межатомных векторов). Для построений ф-ций Патерсона нек-рой структуры, состоящей из N атомов, перенесём её параллельно самой себе так, чтобы в фиксир. начало координат попал сначала первый атом. Векторы от начала координат до всех атомов структуры (включая вектор нулевой длины до первого атома) укажут положения N максимумов ф-ции межатомных векторов, совокупность к-рых наз. изображением структуры в атоме 1. Добавим к ним ещё N максимумов, положение к-рых укажет N векторов от второго атома, помещённого с помощью параллельного переноса в то же начало координат. Проделав эту процедуру со всеми N атомами (рис. 5), получим N2 векторов. Ф-ция, описывающая их. положение, и есть ф-ция Патерсона Р(u, v, w) (u, v, w — координаты точек в пр-ве межатомных векторов).

Для ф-ции Р (u, v, w) можно получить выражение:

P(u, v, w)=2/VShkl?Fhkl?2cos2p(hu+kv+lw),

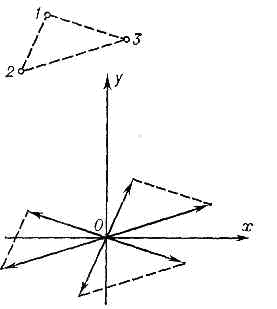Рис. 5. Схема построения ф-ции Патерсона для структуры, состоящей из трёх атомов.

из к-рого следует, что она определяется модулями структурных амплитуд, не зависит от их фаз и, следовательно, может быть вычислена непосредственно по данным дифракц. эксперимента. Трудность интерпретации ф-ции P(u, v, w) состоит в необходимости нахождения координат N атомов из N2 её максимумов, многие из к-рых сливаются из-за того, что межатомные векторы часто перекрываются. Наиболее прост для расшифровки случай, когда в структуре содержится один тяжёлый и неск. лёгких атомов. Изображение •такой структуры в тяжёлом атоме будет значительно отличаться от др. её изображений. Среди разл. методик, позволяющих определить модель исследуемой структуры по ф-ции Патерсона, наиболее эффективными оказались т. н. суперпозиц. методы, к-рые позволили формализовать анализ и выполнять его на ЭВМ.

Другой класс методов нахождения структуры но рентг. дифракц. данным — т. н. прямые методы определения фаз. Учитывая условие положительности электронной плотности в кристалле, можно получить большое число неравенств, к-рым подчиняются коэфф. Фурье (структурные амплитуды). Методами неравенств можно сравнительно просто анализировать структуры, содержащие до 20—40 атомов в элем. ячейке кристалла. Для более сложных структур применяются методы, к-рые основаны на вероятностном подходе, реализованы на ЭВМ и позволяют расшифровывать структуры, содержащие 100—200 и более атомов в элем. ячейке кристалла.

Итак, если фазы структурных амплитуд установлены, то может быть вычислено но (2) распределение электронной плотности в кристалле, причём максимумы этого распределения соответствуют положениям атомов в структуре (рис. 6). Заключит. уточнение координат атомов проводится на ЭВМ, в зависимости от качества эксперимента и сложности структуры их получают с точностью до тысячных долей А. С помощью совр. дифракц. эксперимен та можно вычислять также количеств. хар-ки тепловых колебаний атомов в кристалле с учётом анизотропии этих колебаний.

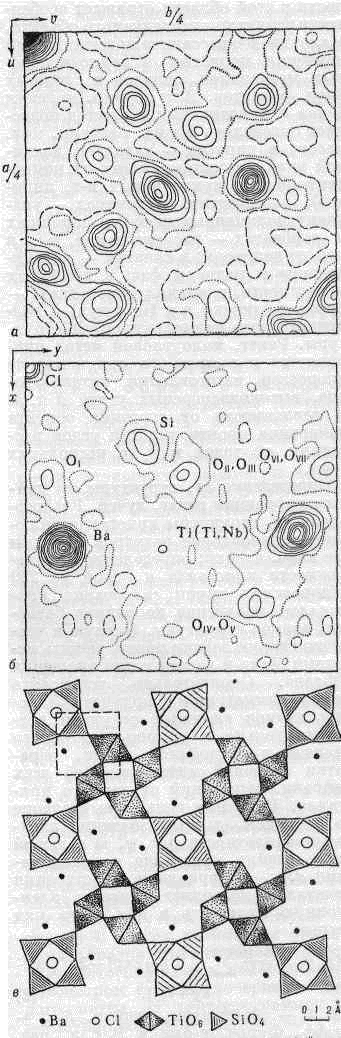Рис. 6. а — проекция на плоскость аb ф-ции межатомных векторов минерала баотита (Ba4Ti4(Ti, Nb)4(Si4Ol2)O16,Cl). Линии проведены через одинаковые значения ф-ции межатомных векторов (линии равного уровня); б — проекция электронной плотности баотита на плоскость аb, полученная расшифровкой ф-ции межатомных векторов. Максимумы электронной плотности (сгущения линий равного уровня) отвечают положениям атомов в структуре; в — изображение модели ат. структуры баотита. Каждый атом Si расположен внутри тетраэдра, образованного четырьмя атомами О; атомы Ti и Nb в октаэдрах, составленных атомами О. Тетраэдры SiO4 и октаэдры Ti(Nb)O6 в структуре баотита соединены, как показано на рис. Часть элем. ячейки кристалла, соответствующая рис. a и б, выделена штриховой линией. Точечные линии на рис. а и б определяют нулевые уровни значений соответствующих ф-ций.

Р. с. а. даёт возможность установить и более тонкие хар-ки ат. структур, напр. распределение валентных эл-нов в кристалле (эта задача решена пока только для простейших структур). Весьма перспективно для этой цели сочетание нейтронографич. и рентгенографич. исследований: нейтронографич. данные о координатах ядер атомов сопоставляют с распределением в пр-ве электронного облака. Для мн. физ. и хим. задач совместно используют Р. с. а. и резонансные методы (см. ЭЛЕКТРОННЫЙ ПАРАМАГНИТНЫЙ РЕЗОНАНС, ЯДЕРНЫЙ МАГНИТНЫЙ РЕЗОНАНС). Фазы структурных амплитуд белковых кристаллов можно определить только в результате совместных рентгеноструктурных и биохим. исследований. При исследовании белков методами Р. с. а. необходимо закристаллизовать как сам белок, так и его производные, полученные введением в них низкомолекулярных соединений, содержащих тяжёлые атомы. Таким способом исследуют белковые кристаллы, в элем. ячейке к-рых может находиться до десятков тысяч атомов.

О многочисл. применениях методов Р. с. а. для исследования нарушений структуры тв. тел (см. РЕНТГЕНОГРАФИЯ МАТЕРИАЛОВ).

РЕНТГЕНОВСКИЙ СТРУКТУРНЫЙ АНАЛИЗ

(рентгеноструктурный анализ)- методы исследования атомного строения вещества по распределению в пространствеи интенсивностям рассеянного на анализируемом объекте рентг. излучения. Р. с. а. кристаллич. материалов позволяет устанавливать координаты атомовс точностью до 0,1-0,01 нм, определять характеристики тепловых колебанийэтих атомов, включая анизотропию и отклонения от гармонич. закона, получатьпо эксперим. дифракц. данным распределения в пространстве плотности валентныхэлектронов на хим. связях в кристаллах и молекулах. Этими методами исследуютсяметаллы и сплавы, минералы, неорганич. и органич. соединения, белки, нуклеиновыекислоты, вирусы. Спец. методы Р. с. а. позволяют изучать полимеры, аморфныематериалы, жидкости, газы.

Среди дифракц. методов исследования атомного строения вещества Р. с. а. является наиб. распространённым и развитым. Его возможности дополняютметоды нейтронографии и электронографии. Дифракц. картиназависит от атомного строения изучаемого объекта, характера и длины волнырентг. излучения. Для установления атомного строения вещества наиб. эффективноиспользование рентг. излучения с длиной волны 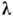~ 10 нм и меньше, т. е. порядка размеров атомов. Особенно успешно и с высокойточностью методами Р. с. а. исследуют атомное строение кристаллич. объектов, структура к-рых обладает строгой периодичностью, и они, т. о., представляютсобой естеств. трёхмерную дифракц. решётку для рентг. излучения.

Историческая справка

В основе Р. с. а. кристаллич. вещества лежит учение о симметрии кристаллов. В 1890 рус. кристаллограф Е. С. Фёдоров и нем. математик А. Шёнфлис (A.Schonflis) завершили вывод 230 пространственных групп симметрии, характеризующихвсе возможные способы размещения атомов в кристаллах. Дифракция рентг. лучей на кристаллах, составляющая эксперим. фундамент Р. с. а., была открытав 1912 М. Лауэ (М. Laue) п его сотрудниками В. Фридрихом (W. Friedrich)и П. Книппингом (P. Knipping). Разработанная Лауэ теория дифракции рентг. лучей на кристаллах позволила связать длину волны излучения 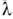,линейные размеры элементарной ячейки кристалла а, b, с, углы падающего 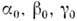и дифракционного 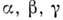лучейсоотношениями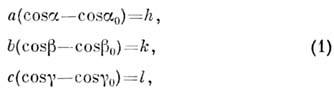

где h, k, l - целые числа ( индексы кристаллографические). Соотношения (1) получили название ур-ний Лауэ, выполнение их необходимодля возникновения дифракции рентг. лучей на кристалле. Смысл ур-ний (1)в том, что разности хода между параллельными лучами, рассеянными атомами, отвечающими соседним узлам решётки, должны быть целыми кратными .

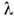В 1913 У. Л. Брэгг (W. L. Bragg) и Г. В. Вульф показали, что дифракц. рентг. пучок можно рассматривать как отражение падающего луча от нек-ройсистемы кристаллографич. плоскостей с межплоскостным расстоянием d: 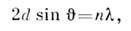где 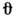- угол между отражающей плоскостью и дифракц. лучом (угол Брэгга). В 1913-14У. Г. и У. Л. Брэгги впервые использовали дифракцию рентг. лучей для эксперим. проверки предсказанного ранее У. Барлоу (W. Barlow) атомного строения кристалловNaCl, Си, алмаза и др. В 1916 П. Дебай (P. Debye) и П. Шеррер (P. Scherrer)предложили и разработали дифракц. методы рентгеноструктурных исследованийполикристаллич. материалов ( Дебая - Шеррера метод).

В качестве источника рентг. излучения использовались (и используютсяпоныне) отпаянные рентг. трубки с анодами из разл. металлов и, следовательно, с различными 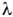соответствующего характеристич. излучения - Fe (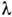= 19,4 нм), Си (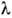= 15,4 нм), Мо (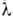= 7,1 нм), Ag (= 5,6 нм). Позднее появились на порядок более мощные трубки с вращающимсяанодом, для структурных исследований используют также наиб. мощный, имеющийбелый (непрерывный) спектр излучения источник - рентг. синхротронноеизлучение. С помощью системы монохроматоров можно непрерывным образомизменять 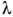применяемого в исследовании синхретронного рентг. излучения, что имеетпринципиальное значение при использовании в Р. с. а. эффектов аномальногорассеяния. В качестве детектора излучения в Р. с. а. служит рентг. фотоплёнка, к-рую вытесняют сцинтилляционные и полупроводниковые детекторы. Эффективностьизмерит. систем резко возросла с применением координатных одномерных идвумерных детекторов.

Количество п качество информации, получаемой с помощью Р. с. а., зависятот точности измерений и обработки эксперим. данных. Алгоритмы обработкидифракц. данных определяются используемым приближением теории взаимодействиярентг. излучения с веществом. В 1950-х гг. началось применение ЭВМ в техникерентгеноструктурного эксперимента и для обработки эксперим. данных. Созданыполностью автоматизированные системы для исследования кристаллич. материалов, к-рые проводят эксперимент, обработку эксперим. данных, осн. процедурыпо построению и уточнению атомной модели структуры и, наконец, графич. представление результатов исследования. Однако с помощью этих систем поканельзя изучать в автоматич. режиме кристаллы с псевдосимметрией, двойниковыеобразцы и кристаллы с др. особенностями структуры.

Экспериментальные методы рентгеновского структурного анализа

Для реализации условий дифракции (1) и регистрации положения в пространствеи интенсивностей дифрагированного рентг. излучения служат рентг. камерыи рентг. дифрактометры с регистрацией излучения соответственно фотогр. методами или детекторами излучения. Характер образца (монокристалл илиполикристалл, образец с частично упорядоченной структурой или аморфноетело, жидкость пли газ), его размер и решаемая задача определяют необходимуюэкспозицию и точность регистрации рассеянного рентг. излучения и, следовательно, определённый метод Р. с. а. Для изучения монокристаллов при использованиив качестве источника рентг. излучения отпаянной рентг. трубки достаточенобъём образца ~10^-3 мм ³. Для получения качественнойдифракц. картины образец должен обладать возможно более совершенной структурой, причём его блочность не препятствует структурным исследованиям. Реальноестроение крупных, почти совершенных монокристаллов исследует рентгеновскаятопография, к-рую иногда тоже относят к Р. с. а.

Метод Лауэ - простейший метод получения рентгенограмм монокристаллов. Кристалл в эксперименте Лауэ неподвижен, а используемое рентг. излучениеимеет непрерывный спектр. Расположение дифракц. пятен на лауэграммах зависитот размеров элементарной ячейки и симметрии кристалла, а также иот ориентации образца относительно падающего рентг. луча. Метод Лауэ позволяетотнести монокристалл к одной из 11 лауэвских групп симметрии и установитьориентацию его кристаллографич. осей с точностью до угл. минут (см. Лауэметод). По характеру дифракц. пятен на лауэграммах и особенно по появлениюастеризма (размытия пятен) можно выявить внутр. напряжения и нек-рые др. особенности строения образца. Методом Лауэ проверяют качество монокристаллови проводят отбор наиб. совершенных образцов для более полного структурногоисследования (рентгенгониометрич. методами; см. ниже).

Методами качания и вращения образца определяют периоды повторяемости(трансляции) вдоль заданных кристаллографич. направлений, проверяют симметриюкристалла, а также измеряют интенсивности дифракц. отражений. Образец вовремя эксперимента приводится в колебат. или вращат. движение относительнооси, совпадающей с одной из кристаллографич. осей образца, к-рую предварительноориентируют перпендикулярно падающему рентг. лучу. Дифракц. картина, создаваемаямонохроматич. излучением, регистрируется на рентг. плёнке, находящейсяв цилиндрич. кассете, ось к-рой совпадает с осью колебания образца. Дифракц. пятна при такой геометрии съёмки на развёрнутой плёнке оказываются расположеннымина семействе параллельных прямых (рис. 1). Период повторяемости Т вдолькристаллографич. направления равен:

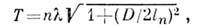
где D - диаметр кассеты,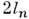- расстояние между соответствующими прямыми на рентгенограмме. Т. к.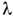постоянна, условия Лауэ (1) выполняются за счёт изменения углов при качанииили вращении образца. Обычно на рентгенограммах качания и вращения образцадифракц. пятна перекрываются. Чтобы избежать этого нежелательного эффекта, можно уменьшить угл. амплитуду колебаний образца. Такой приём применяют, напр., в Р. с. а. белков, где рентгенограммы качания используют для измеренияинтенсивностей дифракц. отражений.

Рис. 1. Рентгенограмма качания минерала сейдозерита Na₄MnTi(Zr,Ti)₂0₂(F,OH)₂[Si₂O₇]₂.

Рентгенгониометрические методы. Для полного структурного исследованиямонокристалла методами Р. с. а. необходимо определить положение в пространствеи измерить интегральные интенсивности всех дифракц. отражений, возникающихпри использовании излучения с данной 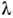.Для этого в процессе эксперимента образец должен с точностью порядка угл. минут принимать ориентации, при к-рых выполняются условия (1) последовательнодля всех семейств кристаллографич. плоскостей образца; при этом регистрируютсямн. сотни и даже тысячи дифракц. рефлексов. При регистрации дифракц. картинына рентг. фотоплёнке интенсивности рефлексов определяются микроденситометромпо степени почернения и размеру дифракц. пятен. В разл. типах гониометровреализуются разл. геом. схемы регистрации дифракц. картины. Полный наборинтенсивностей дифракц. отражений получают на серии рентгенограмм, на каждойрентгенограмме регистрируются рефлексы, на кристаллографич. индексы к-рыхналожены определ. ограничения. Напр., на разных рентгенограммах регистрируютсяотражения типа hk0, hk1 (рис. 2). Для установленияатомной структуры кристалла, в элементарной ячейке к-рого содержится ~100атомов, необходимо измерить неск. тысяч дифракц. отражений. В случае монокристалловбелков объём эксперимента возрастает до 10⁴-10⁶ рефлексов.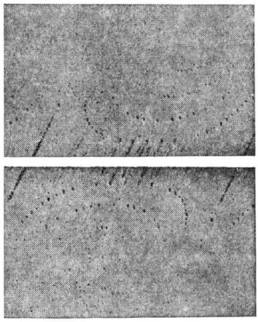

Рис. 2. Рентгенограмма минерала сейдозерита, полученная в рентгеновскомгониометре Вайсенберга. Зарегистрированные дифракционные отражения имеютиндексы 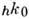.Отражения, расположенные на одной кривой, характеризуются постоянным индексомk.

При замене фотоплёнки на счётчики рентг. квантов возрастают чувствительностьи точность измерения интенсивностей дифракц. отражений. В совр. автоматич. дифрактометрах предусмотрены 4 оси вращения (3 у образца и 1 у детектора),что позволяет реализовать в них различные по геометрии методы регистрациидифракц. отражений. Такой прибор универсален, управление им осуществляетсяс помощью ЭВМ и специально разработанных алгоритмов и программ. НаличиеЭВМ позволяет ввести обратную связь, оптимизацию измерений каждого дифракц. отражения и, следовательно, естеств. образом планировать весь дифракц. эксперимент. Измерения интенсивностей производятся с необходимой для решаемойструктурной задачи статистич. точностью. Однако увеличение точности измеренияинтенсивностей на порядок требует увеличения времени измерений на два порядка. На точность измерений накладывает ограничение качество исследуемого образца. Для белковых кристаллов (см. ниже) сокращение времени эксперимента осуществляетсяза счёт использования двумерных детекторов, в к-рых параллельно идёт измерениемн. десятков дифракц. отражений. При этом утрачивается возможность оптимизацииизмерений на уровне отд. рефлекса.

Метод исследования поликристаллов (метод Дебая - Шеррера). Для Р. с. а. кристаллич. порошков, керамич. материалов и др. поликристаллич. объектов, состоящих из большого числа мелких, случайным образом ориентированных друготносительно друга монокристаллов, используется монохроматич. рентг. излучение. Рентгенограмма от поликристаллич. образца (де-баеграмма) представляет собойсовокупность концент-рич. колец, каждое из к-рых состоит из дифракц. отраженийот разл. образом ориентированных в разных зёрнах систем кристаллографич. плоскостей с определённым межплоскостным расстоянием d. Набор . и соответствующие им интенсивности дифракц. отражений индивидуальныдля каждого кристаллич. вeщества. Метод Дебая - Шеррера используется приидентификации соединений и анализе смесей поликристаллич. веществ по качеств. и количеств. составу составляющих смеси фаз. Анализ распределения интенсивностейв дебаевских кольцах позволяет оценить размеры зёрен, наличие напряженийи преимущественных ориентации (текстурирования) в расположении зёрен (см. Рентгенография материалов, Дебая - Шеррера метод).

В 1980 - 90-х гг. в Р. с. а. стал применяться метод уточнения атомногостроения кристаллич. веществ по дифракц. данным от поликристаллич. материалов, предложенный X. М. Ритвелдом (Н. М. Rietveld) для нейтронографич. исследований. Метод Рптвелда (метод полнопрофильного анализа) используется в том случае, когда известна приближённая структурная модель изучаемого соединения, поточности результатов он может конкурировать с рентгеноструктурными методамиисследования монокристаллов.

Исследование аморфных материалов и частично упорядоченных объектов. Чем ниже степень упорядоченности атомного строения анализируемого вещества, тем более размытый, диффузный характер имеет рассеянное им рентг. излучение. Однако дифракц. исследования даже аморфных объектов дают возможность получитьинформацию об их строении. Так, диаметр диффузного кольца на рентгенограммеот аморфного вещества (рис. 3) позволяет оценить ср. межатомные расстоянияв нём. С ростом степени упорядоченности в строении объектов дифракц. картинаусложняется (рис. 4) и, следовательно, содержит больше структурной информации.

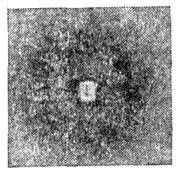
Рис. 3. Рентгенограмма аморфного вещества - ацетата целлюлозы.

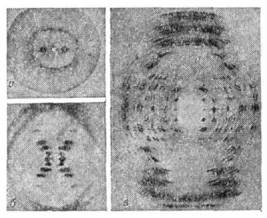
Рис. 4. Рентгенограммы биологических объектов: а - волоса; б - натриевойсоли ДНК во влажном состоянии; в - текстуры натриевой соли ДНК.

Метод малоуглового рассеяния. В том случае, когда размеры неоднородностейв объекте исследования превышают межатомные расстояния и составляют от0,5-1 до 10³ нм, т. е. во много раз превышают длину волны используемогоизлучения, рассеянное рентг. излучение концентрируется вблизи первичногопучка - в области малых углов рассеяния. Распределение интенсивности вэтой области отражает особенности строения исследуемого объекта. В зависимостиот строения объекта и размеров неоднородностей интенсивность рентг. рассеянияизмеряют в углах от долей минуты до неск. градусов.

Малоугл. рассеяние применяют для изучения пористых и мелкодисперсныхматериалов, сплавов и биол. объектов. Для молекул белка и нуклеиновых кислотв растворах метод позволяет с невысоким разрешением определять форму иразмеры индивидуальной молекулы, мол. массу, в вирусах - характер взаимнойукладки составляющих их компонент (белка, нуклеиновых кислот, липидов),в синтетич. полимерах - упаковку полимерных цепей, в порошках и сорбентах- распределение частиц и пор по размерам, в сплавах - фиксировать возникновениеновых фаз и определять размеры этих включений, в текстурах (в частности, в жидких кристаллах) - упаковку частиц (молекул) в различного рода надмолекулярныеструктуры. Эффективным оказался метод малоугл. рассеяния и для исследованиястроения ленгмюровских плёнок. Он применяется также в пром-сти при контролепроцессов изготовления катализаторов, высокодисперсных углей и т. д.

Анализ атомной структуры кристаллов

Определение атомной структуры кристаллов включает: установление формыи размеров элементарной ячейки, симметрии кристалла (его принадлежностик одной из 230 фёдоровских групп) и координат базисных атомов структуры. Прецизионные структурные исследования позволяют, кроме того, получать количеств. характеристики тепловых движений атомов в кристалле и пространственноераспределение в нём валентных электронов. Методами Лауэ и качания образцаопределяют метрику кристаллич. решётки. Для дальнейшего анализа необходимоизмерение интенсивностей всех возможных дифракц. отражений от исследуемогообразца при данной l. Первичная обработка эксперим. данных учитывает геометриюдифракц. эксперимента, поглощение излучения в образце, поляризацию и др. более тонкие эффекты взаимодействия излучения с образцом.

Трёхмерная периодичность кристалла позволяет разложить распределениеего электронной плотности 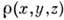в пространстве в ряд Фурье: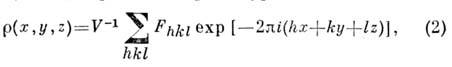

где V - объём элементарной ячейки кристалла, F_hkl- коэффициенты Фурье, к-рые в Р. с. а. наз. структурными амплитудами. Каждая структурная амплитуда характеризуется целыми числами h, k, l- кристаллографич. индексами в соответствии с (1) и однозначно отвечаетодному дифракц. отражению. Разложение (2) физически реализуется в дифракц. эксперименте.

Осн. сложность структурного исследования состоит в том, что обычныйдифракц. эксперимент даёт возможность измерить интенсивности дифракц. пучков I_hkl но не позволяет фиксировать их фазы 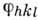.Для мозаичного кристалла в кинематич. приближении 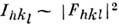. Анализ эксперим. массива 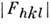с учётом закономерных погасаний рефлексов позволяет однозначно установитьего принадлежность к одной из 122 рентг. групп симметрии. При отсутствиианомального рассеяния дифракц. картина всегда центросимметрична. Для определенияфёдоровской группы симметрии необходимо независимо выяснить, обладает ликристалл центром симметрии. Эта задача может быть решена на основе анализааномальной составляющей рассеяния рентг. лучей. При отсутствии последнегостроят кривые статистич. распределения 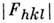по их значениям, эти распределения различны для центросимметричных и ацентричныхкристаллов. Отсутствие центра симметрии может быть однозначно установленои по физ. свойствам кристалла (пироэлектрическим, сегнетоэлектрическими др.).

Фурье-преобразование соотношения (2) позволяет получить расчётные ф-лыдля вычисления величин F_hkl (в общем случае - комплексных):

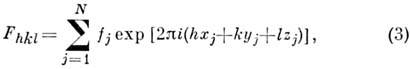
где 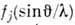- ат. фактор рассеяния рентг. излучения атомом j_j, x_j,y_j, z_j - его координаты; суммирование идёт повсем N атомам элементарной ячейки.

Задача, обратная структурному исследованию, решается следующим образом:если известна атомная модель структуры, то по (3) вычисляются модули ифазы структурных амплитуд и, следовательно, интенсивности дифракц. отражений. Дифракц. эксперимент даёт возможность измерить мн. сотни не связанных симметриейамплитуд 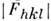, каждая из к-рых определяется по (3) набором координат базисных (независимыхпо симметрии) атомов структуры. Таких структурных параметров существенноменьше, чем модулей 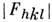,следовательно, между последними должны существовать связи. Теория структурногоанализа установила связи разного типа: неравенства, линейные неравенства, структурные произведения и детерминанты связи структурных амплитуд.

На основе наиб, эффективных статистич. связей развиты [Дж. Карле (J.Karle) и X. А. Хауптман (Н. A. Hauptman), Нобелевская премия, 1985] т. н. прямые методы определения фаз структурных амплитуд. Если взять тройкубольших по модулям структурных амплитуд, индексы к-рых связаны простымисоотношениями h₁ + h₂ + h₃ = 0, k₁+ k₂+ k₃ = 0, l₁ + l₂ + l₃= 0, то наиб. вероятная сумма фаз этих амплитуд будет равна нулю:

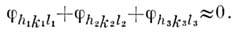
Вероятность выполнения равенства тем выше, чем больше произведение спец. образом нормированных структурных амплитуд, входящих в это соотношение. С ростом числа атомов N в элементарной ячейке кристалла надёжностьсоотношения падает. На практике используются существенно более сложныестатистич. соотношения и достаточно строгие оценки вероятностей выполненияэтих соотношений. Вычисления по этим соотношениям весьма громоздки, алгоритмысложны и реализуются только на мощных совр. ЭВМ. Прямые методы дают первыеприближённые значения фаз и только наиб. сильных по нормированным модулямструктурных амплитуд.

Для практики структурных исследований важны процедуры автоматич. уточненияфаз структурных амплитуд. На основе приближённого набора фаз 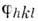сильнейших структурных амплитуд и по соответствующим эксперим. модулям 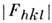по (2) вычисляется первое приближённое распределение электронной плотностив кристалле 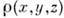.Затем 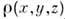модифицируется на основе физ. и кристаллохим. информации о свойствах этогораспределения. Напр., во всех точках пространства 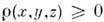,по модифициров. распределению 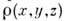путём обращения Фурье вычисляются уточнённые фазы 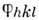и вместе с эксперим. значениями 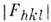используются для построения следующего приближения 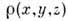и т. д. После получения достаточно точных значений 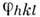по(2) строится трёхмерное распределение электронной плотности в кристалле. Оно по существу является изображением исследуемой структуры, и вся сложностьего получения вызвана отсутствием собирающих линз для рентг. излучения.

Правильность полученной атомной модели проверяют сравнением эксперим.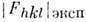и вычисленных 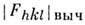по (3) модулей структурных амплитуд. Количеств. характеристика такого сравнения- фактор расходимости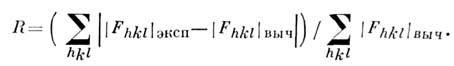

Этот фактор даёт возможность методом проб и ошибок получить оптим. результаты. Для некристаллич. объектов это практически единств. метод интерпретациидифракц. картины.

Определение фаз структурных амплитуд прямыми методами осложняется приувеличении числа атомов в элементарной ячейке кристалла. Псевдосимметрияи нек-рые др. особенности его строения также ограничивают возможности прямыхметодов.

Иной подход к определению атомного строения кристаллов по рентг. дифракц. данным был предложен А. Л. Патерсоном (A. L. Paterson). Атомная модельструктуры строится на основе анализа ф-ции межатомных векторов P(u,v,w )(ф-ции Патерсона), к-рая вычисляется по эксперим. значениям 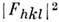. Смысл этой ф-ции можно пояснить с помощью схемы её геом. построения. Атомную структуру, содержащую в элементарной ячейке N атомов, помещаемпараллельно самой себе так, чтобы первый атом попал в начало координат. Если умножить атомные веса всех атомов структуры на значение атомного весапервого атома, то получим веса первых N пиков ф-ции межатомных векторов. Это т. н. изображение структуры в первом атоме. Затем в начало координатпомещаем таким же образом построенное изображение структуры во втором атоме, затем в третьем и т. д. Проделав эту процедуру со всеми N атомамиструктуры, получим N² пиков ф-ции Патерсона (рис. 5).Т. к. атомы не являются точками, полученная ф-ция P(u,v,w )содержитдостаточно размытые и перекрывающиеся пики: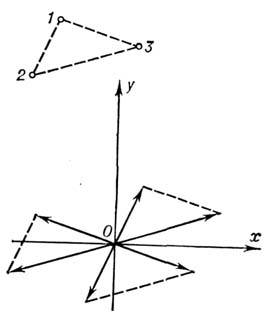

Рис. 5. Схема построения функции межатомных векторов для структуры, состоящей из трёх атомов.

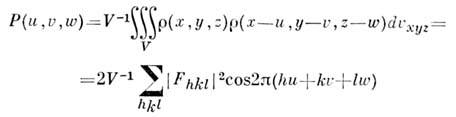
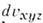[ - элементобъёма в окрестности точки ( х, у,z)]. Ф-ция межатомных векторов строитсяпо квадратам модулей эксперим. структурных амплитуд и является свёрткойраспределения электронной плотности 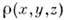с собой, но после инверсии в начале координат.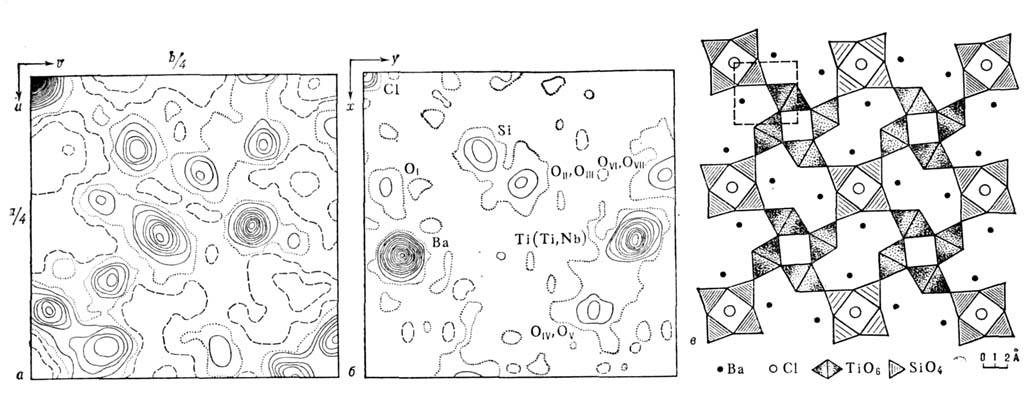

Рис. 6. Минерал баотит Ba₄Ti₄(Ti,Nb)₄[Si₄O₁₂]O₁₆Cl;a - функция межатомных векторов, проекция на плоскость аb, линии равногоуровня значений функции проведены через равные произвольные интервалы;б - проекция распределения электронной плотности на плоскость аb, полученнаяпутём интерпретации функции межатомных векторов и уточнения атомной модели, сгущения линий равного уровня отвечают положениям атомов в структуре; в- проекция атомной модели структуры на плоскость аb в полинговских полиэдрах. Атомы Si расположены внутри тетраэдров из атомов кислорода, атомы Ti иNb находятся в октаэдрах из атомов кислорода. Тетраэдры [SiO₄]и октаэдры [Ti(Nb)O₆] в структуре баотита соединены, как показанона рисунке. Атомы Ва и С1 показаны черными и светлыми кружками. Часть элементарнойячейки кристалла, изображённая на рисунках а и б, отвечает на рисунке вквадрату, выделенному штриховыми линиями.

Трудности интерпретации P(u,v,w )связаны с тем, что среди N² пиков этой ф-ции необходимо распознать пики одного изображения структуры. Максимумы ф-ции Патерсона существенно перекрываются, что ещё более осложняетеё анализ. Наиб. прост для анализа случай, когда исследуемая структурасостоит из одного тяжёлого атома и неск. значительно более лёгких атомов. В этом случае изображение структуры в тяжёлом атоме рельефно выступаетна фоне остальных пиков P(u,v,w). Разработан ряд методов систематич. анализа ф-ции межатомных векторов. Наиб. эффективными из них являются суперпозиц. методы, когда две или более копий P(u,v,w) в параллельном положениинакладываются друг на друга с соответствующими смещениями. При этом закономерносовпадающие на всех копиях пики выделяют одно или несколько из N исходных изображении структуры. Как правило, для единств. изображения структурыприходится использовать дополнит. копии P(u,v,w). Проблема сводитсяк поиску необходимых взаимных смещений этих копий. После локализации насуперпозиц. синтезе приближённого распределения атомов в структуре этотсинтез может быть подвергнут обращению Фурье и т. о. он позволяет получитьфазы структурных амплитуд. Последние вместе с эксперим. значениями 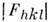используются для построения 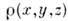.Все процедуры суперпозиц. методов алгоритмизированы и реализованы в автоматич. режиме на ЭВМ. На рис. 6 изображено атомное строение кристалла, установленноесуперпозиционными методами по ф-ции Патерсона.

Разрабатываются эксперим. методы определения фаз структурных амплитуд. Физ. основой этих методов служит эффект Реннингера - многолучевая рентг. дифракция. При наличии одноврем. рентг. дифракц. отражений имеет местоперекачка энергии между ними, к-рая зависит от фазовых соотношений междуданными дифракц. пучками. Вся картина изменения интенсивностей при этомограничена угл. секундами и для массовых структурных исследований эта методикапрактич. значения пока не приобрела.

В самостоят. раздел Р. с. а. выделяют прецизионные структурные исследованиякристаллов, позволяющие получать по дифракц. данным не только модели атомногостроения исследуемых соединений, но и количеств. характеристики тепловыхколебаний атомов, включая анизотропию этих колебаний (рис. 7) и их отклоненияот гармонич. закона, а также пространственное распределение валентных электроновв кристаллах. Последнее важно для исследования связи между атомным строениеми физ. свойствами кристаллов. Для прецизионных исследований разрабатываютсяспец. методы эксперим. измерений и обработки дифракц. данных. В этом случаенеобходимы учёт одноврем. отражений, отклонений от кинематичности дифракции, принятие во внимание динамич. поправок теории дифракции и др. тонких эффектоввзаимодействия излучения с веществом. При уточнении структурных параметровиспользуют метод наим. квадратов, причём важнейшее значение имеет учёткорреляции между уточняемыми параметрами.

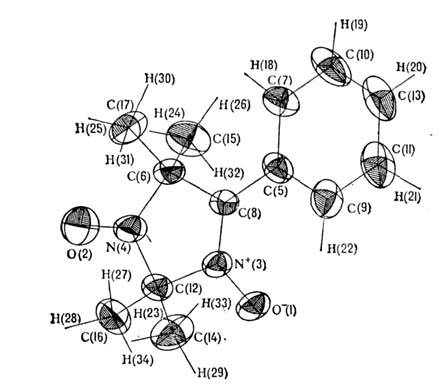
Рис. 7. Эллипсоиды анизотропных тепловых колебаний атомов стабильногонитрон-сильного радикала C₁₃H₁₇N₂O₂.

Р. с. а. используют для установления связи атомного строения с физ. свойствами сегнетоэлектриков, суперионных проводников, лазерных и нелинейныхоптич. материалов, высокотемпературных сверхпроводников и др. МетодамиР. с. а. получены уникальные результаты при исследовании механизмов фазовыхпереходов в твёрдом теле и биол. активности макромолекул. Так, анизотропияпоглощения акустич. волн в монокристаллах парателлурита 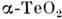связана с энгармонизмом тепловых колебаний атомов Те (рис. 8). Упругиесвойства тетрабората лития Li₂B₄ О ₇, открывающиедля него перспективы применения в качестве детектора акустич. волн, обусловленыхарактером хим. связей в этом соединении. С помощью Р. с. а. исследуютраспределение в кристалле валентных электронов, реализующих межатомныесвязи в нём. Эти связи могут исследоваться с помощью распределения деформац. электронной плотности, представляющей собой разность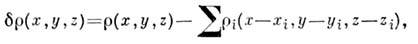

где 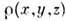- распределение электронной плотности в кристалле,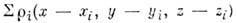- сумма сферически симметричных плотностей свободных (не вступивших в хим. связи) атомов данной структуры, к-рые расположены соответственно в точкахс координатами x_i, y_i, z_i. Приустановлении по рентг. дифракц. данным деформац. электронной плотностинаиб. сложен учёт тепловых колебаний атомов, существ. образом коррелирующихс характером и направлениями хим. связей. Т. о., деформац. плотность отражает перераспределение в пространстве той части электронной плотностиатомов, к-рая непосредственно участвует в образовании хим. связей (рис.9).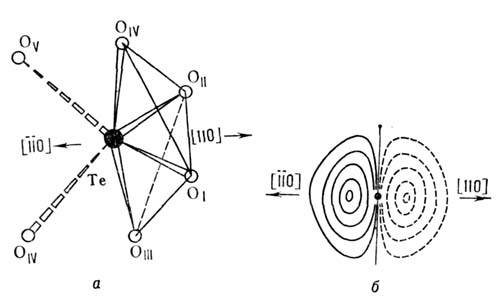

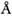Рис. 8. Ближайшее окружение теллура атомами О в структуре (a) и ангармоническая составляющая распределения плотности вероятностинахождения атома Те в данной точке пространства в процессе тепловых колебаний(б). Положительные (сплошные) и отрицательные (штриховые) линии равногоуровня проведены через 0,02^-3.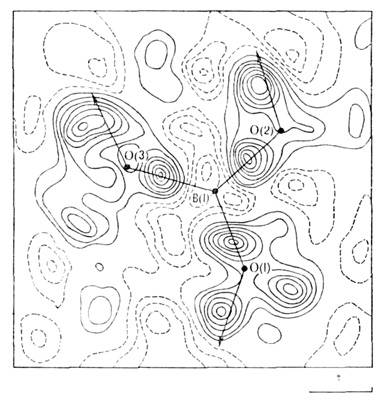

Рис. 9. Сечение синтеза деформационной электронной плотности кристаллаLi₂B₄O₇ плоскостью, проходящей через атомыО треугольной группы ВО ₃, в центре которой находится атом В. Максимумы на отрезках В - О указывают на ковалентный характер связей междуэтими атомами. Штриховыми линиями выделены области, из которых электроннаяплотность переместилась на химические связи. Линии равного уровня проведенычерез 0,2.

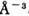
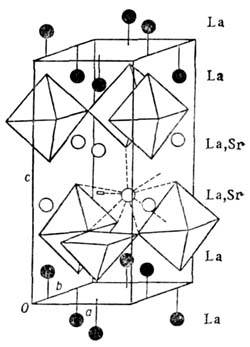
Рис. 10. Упорядоченное размещение атомов Sr по позициям лантана вструктуре 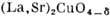Атомы Сu

Структурные исследования высокотемпературных сверхпроводников позволилиустановить их атомное строение и его связь с их физ. свойствами. Было показано, что в монокристаллах 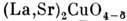темп-ра перехода в сверхпроводящее состояние Т _с зависитне только от кол-ва Sr, но и от способа его статистич. размещения. Равномерноераспределение атомов Sr в структуре является оптимальным для сверхпроводящихсвойств. Концентрация Sr в определ. слоях структуры (рис. 10) ведёт к потерев этих слоях части кислорода и к понижению Т _с. Для кристаллов 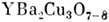методами Р. с. а. установлено упорядочение в размещении атомов О. В пределаходного кристалла установлено наличие ромбических по симметрии областейлокального состава 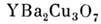с Т _с~90 К и областей находятся в [СuО ₆]-октаэдрах. Дефектность по кислороду показана отсутствием у одного из Cu-полиэдроводной кислородной вершины. Позиции, полностью заселённые атомами La, показанычёрными кружками. Светлые кружки - позиции лантана, в которых сконцентрированыи статистически размещены все атомы Sr.

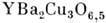с Т _с~60 К. В кристаллах с кол-вом кислорода меньше чем 6,5 атома на элементарнуюячейку, наряду с областями ромбич. симметрии локального состава 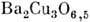появляются области тетрагональной симметрии локального состава 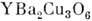,к-рые не переходят в сверхпроводящее состояние.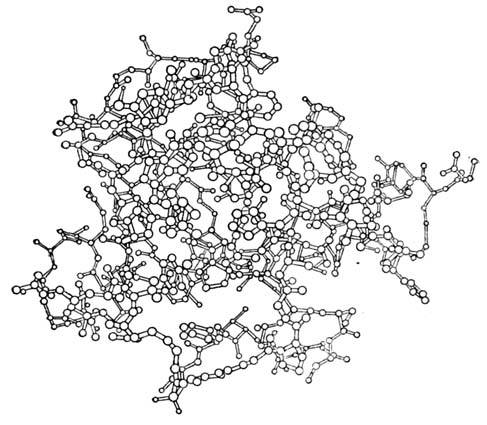

Рис. 11. Атомная модель молекулы гуанил-специфичной рибонуклеазыС ₂, построенная на основе рентгеноструктурного исследованиямонокристаллов этого белка с разрешением 1,55

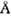
Для решения мн. задач физики твёрдого тела, химии, молекулярной биологиии др. весьма эффективно совместное использование методов рентгеноструктурногоанализа и резонансных методов (ЭПР, ЯМР и др.). При исследовании атомногостроения белков, нуклеиновых к-т, вирусов и др. объектов молекулярной биологиивозникают специфич. сложности. Макромолекулы или. более крупные биол. объектынеобходимо прежде всего получить в монокристаллич. форме, после чего дляих исследования можно применять все методы Р. с. а., развитые для изучениякристаллич. веществ. Проблема фаз структурных амплитуд для белковых кристалловрешается методом изоморфных замещений. Наряду с монокристаллами исследуемогонативного белка получают монокристаллы его производных с тяжелоатомнымидобавками, изоморфными кристаллам исследуемого белка. Разностные ф-цииПатерсона для производных и нативного белка дают возможность локализоватьв элементарной ячейке кристалла положения тяжёлых атомов. Координаты этихатомов и наборы модулей структурных амплитуд белка и его тяжелоатомныхпроизводных используются в спец. алгоритмах для оценки фаз структурныхамплитуд. В белковой кристаллографии применяются поэтапные методы установленияатомного строения макромолекул с последоват. переходом от низкого к болеевысокому разрешению (рис. 11). Разработаны и спец. методы уточнения атомногостроения макромолекул по рентг. дифракц. данным. Объёмы вычислений приэтом столь велики, что эффективно могут быть реализованы только на самыхмощных ЭВМ.

Вопросы Р. с. а., связанные с изучением реального строения твёрдоготела по дифракц. данным, рассмотрены в ст. Рентгенография материалов.

Лит.: Белов Н. В., Структурная кристаллография, М., 1951; Б ок и й Г. Б., Порай-Кошиц М. А., Рентгеноструктурный анализ, 2 изд., т.1, М., 1964; Липсон Г., К о к р е н В., Определение структуры кристаллов, пер. с англ., М., 1956; Бюргер М., Структура кристаллов и векторное пространство, пер. с англ., М., 1961; Г и н ь е А., Рентгенография кристаллвв. Теорияи практика, пер. с франц., М., 1961; Stout G, Н., J е n s е n L. Н., X-raystructure determination, N. Y.- L., 1968; X е и к е р Д. М., Рентгеновскаядифрактометрия монокристаллов, Л., 1973; Бландел Т., Джонсон Л., Кристаллографиябелка, пер. с англ., М., 1979; Вайнштейн Б. К., Симметрия кристаллов. Методыструктурной кристаллографии, М., 1979; Electron and magnetization densitiesin molecules and crystals, ed. by P. Becker, N. Y.- L., 1980; Кристаллографияи кристаллохимия, М., 1986; Structure and physical properties of crystals,Barselona, 1991. В. И. Симонов.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.