Akademik

- утверждает, что кпд hтепловой машины, в к-рой используется Карно цикл, зависит только от темп-р t₁ и t₂ нагревателя и холодильника, но не зависит от природы рабочего вещества. Доказана Н. Л. С. Карно (N. L. S. Carnot) в 1824. Если t₁ и t₂ - эмпирич. темп-ры нагревателя и холодильника, то, согласно К. т.,

h=(Q₁-Q₂)/Q₁=f(t₁, t₂),

где Q₁ - кол-во теплоты, отдаваемое нагревателем, Q₂ - кол-во теплоты, передаваемое холодильнику, f(t₁, t₂) - универсальная ф-ция выбранных эмпирия, темп-р. Теорема о том, что кпд любого теплового двигателя не может превышать кпд цикла Карно, осуществляемого при той же темп-ре нагревателя и холодильника, также наз. К. т. К. т. можно доказать, рассматривая две тепловые машины с общими нагревателем и холодильником, в к-рых цикл Карно осуществляется с разл. рабочими веществами. Если кпд машин различаются, то результат кругового процесса, в к-ром одна машина работает по прямому, а другая - по обратному циклу Карно, противоречит второму началу термодинамики. В том случае, когда в цикле Карно используют идеальный газ, Q₁/Q₂=T₁/T₂,поэтому удобно определить а б с. шкалу темп-р так, чтобы f(T_1, Т₂)=(T₁-T₂)/T₁ (шкала Кельвина). Тогда кпд цикла Карно равен h=(T₁-T₂)/T₁.Любой термодинамич. цикл можно представить состоящим из большого (в пределе - бесконечно большого) числа циклов Карно. Применив к каждому из элементарных циклов К. т., будем иметь причём кол-во теплоты dQ_i,полученное 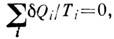системой, считается положительным, а отданное - отрицательным. В пределе для любого обратимого цикла получается равенство Клаузиуса 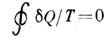, а для необратимого цикла -неравенство Клаузиуса -удобная формулировка второго начала 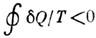термодинамики. Лит. см. при ст. Термодинамика. Д. H.. Зубарев.