Akademik

уравнение, содержащее искомую функцию под знаком несобственного интеграла в смысле главного значения по Коши. В зависимости от размерности многообразия, по к-рому распространены интегралы, различают одномерные и многомерные С. и. у. По сравнению с теорией уравнений Фредгольма теория С. и. у. является более сложной. Так, напр., теории одномерных и многомерных С. и. у. как в смысле формулировок окончательных результатов, так и применяемых для их установления методов значительно отличаются друг от друга. Теория одномерных С. и. у. разработана более полно, причем ее результаты формулируются проще, чем аналогичные результаты в многомерном случае. Ниже в основном будет рассмотрен одномерный случай.

Важным классом одномерных С. и. у. являются уравнения с ядром Коши:

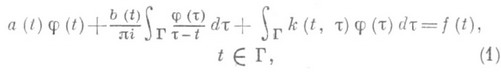
где а, b, k, f - известные функции, из к-рых k- ядро Фредгольма (см. Интегральный оператор),j - искомая функция, Г - плоская линия, а несобственный интеграл понимается в смысле главного значения по Коши, т. е.

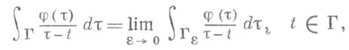
где Г _e=Гl_e , l_e обозначает дугу t'tt " линии Г такую, что длины дуг tt' и tt " равны e.

Оператор К, определяемый левой частью равенства (1), наз. сингулярным оператором (иногда его наз. общим сингулярным оператором):

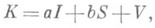(2)

где I - тождественный оператор, S - сингулярный интегральный оператор (иногда его наз. сингулярным интегральным оператором с ядром Коши), т. е.

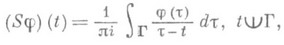
V - интегральный оператор с ядром k(t,t).

Оператор K₀=aI+bS наз. характеристической частью сингулярного оператора К, или характеристическим сингулярным оператором, а уравнение

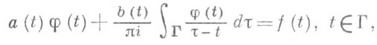(3)

- характеристическим С. и. у., функции а, b - коэффициентами соответствующего оператора или уравнения.

Уравнение

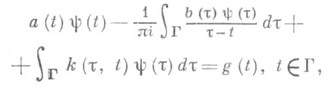
наз. союзнымс уравнением (1), а оператор K'=aI+SbI+V'(V'- интегральный оператор с ядром k(t, t)) - союзным с оператором К. В частности, К'₀=аI+SbI является союзным с К ₀.

Операторы К, К ₀, К', К'₀ или соответствующие им уравнения наз. нормального типа, если функции

А=а+b, В=а-b

не обращаются в нуль нигде на Г. В этом случае говорят также, что коэффициенты оператора или уравнения удовлетворяют условию нормальности.

Пусть 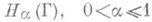,- класс функций {f}, определенных на Г и удовлетворяющих условию

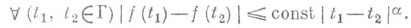
Когда предполагается, что функция f принадлежит классу H_a (Г) при нек-ром допустимом значении a и не требуется знания численного значения a, то будет употребляться обозначение 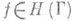или , если из контекста ясно, о какой линии Г идет речь.

Множество Нназ. функциональным классом Гёльдера; если , то говорят, что f удовлетворяет условию Гёльдера или что f является H-функцией.

Пусть G - комплекснозначная непрерывная функция, не обращающаяся в нуль на ориентированной замкнутой простой гладкой линии Г, и

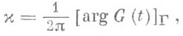(4)

где [ ] _Г обозначает приращение функции, заключенной в скобках, при однократном обходе линии Г в положительном направлении. Целое число 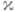наз. индексом функции G:.

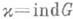Решение характеристического и союзного с ним С. и. у. Пусть Г - простая замкнутая, ориентированная гладкая линия, на к-рой положительное направление выбрано так, что оно оставляет конечную область с границей Г слева, начало координат лежит в этой области и , причем а, b удовлетворяют условию нормальности. Пусть, далее 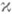определено равенством (4), в к-ром

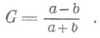(5)

Тогда справедливы следующие утверждения.

1) Если 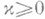, то уравнение (3) разрешимо в классе H(Г) при любой правой части и все его H-решения представляются (см. [1], [2]) формулой

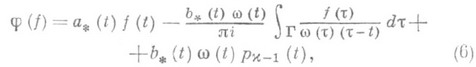
где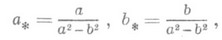

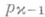- произвольный многочлен степени (p_-1=0). Если 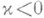, то уравнение (3) разрешимо в классе Н(Г).тогда и только тогда, когда правая часть f удовлетворяет условиям

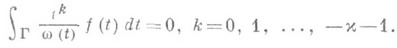
При соблюдении этих условий уравнение (3) имеет единственное H-решение, определяемое формулой (6), в к-рой .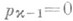

2) Союзное с (3) С. и. у.

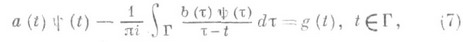
разрешимо в классе H при любой правой части 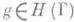, если 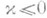, и все его H-решения представляются формулой

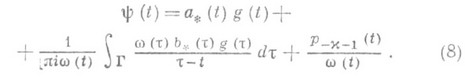
Если же , то уравнение (7) разрешимо тогда и только тогда, когда правая часть gудовлетворяет 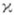условиям:

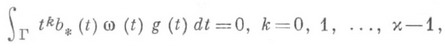
при соблюдении к-рых решение дается формулой (8), где нужно положить

Теоремы Нётера. Пусть v и v' - числа линейно

независимых решений однородных уравнений K'₀j=0 и K'₀y=0 соответственно. Тогда разность v-v' наз. индексом опера тора K₀ или уравнения K₀j=0:

ind K₀ = v- v'.

Теорема 1. Однородные С. и. у. K₀j=0 и K'₀y=0имеют конечное число линейно независимых решений.

Теорема 2. Необходимые и достаточные условия разрешимости неоднородного уравнения (3) заключаются в том, что

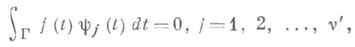
где y₁, . . ., y_g , - полная система линейно независимых решении союзного однородного уравнения K'₀y=0. Теорема 3. Индекс оператора К ₀ равен индексу функции G, определяемой равенством (5), т. е.

(9)

Эти теоремы остаются в силе и в случае общего С. и. у. (1), то есть в сформулированных теоремах операторы К ₀, К'₀ можно заменить операторами К, К'. Надо только иметь в виду, что в случае общих С. и. у. числа v и v', вообще говоря, оба отличны от нуля, в отличие от характеристических С. и. у., когда одно из этих чисел обязательно равно нулю.

Теоремы 1-3 наз. теоремами Нётера, в честь Ф. Нётера (F. Noether), впервые доказавшего их [9] в случае одномерного С. и. у. с Гильберта ядром:

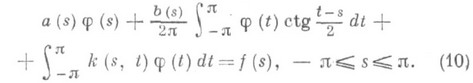
Эти теоремы аналогичны теоремам Фредгольма (см. Фредгольма уравнение).и отличаются от них только тем, что числа линейно независимых решений однородного уравнения и союзного с ним уравнения, вообще говоря, различны, т. е. тогда как индекс уравнения Фредгольма всегда равен нулю, С. и. у. может иметь отличный от нуля индекс.

Формулы (6), (8) так же, как теоремы Нётера, остаются в силе и в случае, когда состоит из конечного числа гладких взаимонепересекающихся замкнутых линий. В этом случае в равенстве (4) символ [ ] _Г обозначает сумму приращений выражения, заключенного в скобках при обходе отдельных линий . Случай же, когда Г- конечная совокупность гладких разомкнутых взаимонепересекающихся линий 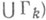, требует специального рассмотрения.

Если функция j является H-функцией внутри каждой из закрытой части линий , не содержащей концов этой линии, вблизи же любого конца спредставима в виде 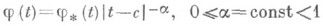, где j_* является H-функцией в окрестности с, включая с, то говорят, что j принадлежит классу H*. Если 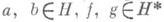и решения уравнений (3), (7) разыскиваются в классе H*, то можно так определить число 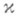и функцию w, что и в этом случае остаются в силе формулы (6), (8). Далее, если соответствующим образом определить подклассы класса H*, в к-рых разыскиваются решения данного и союзного с ним С. и. у., то остаются н силе и теоремы Нётера (см. [1]).

Указанные выше результаты обобщены в различных направлениях. Показано (см. [1]), что при нек-рых условиях они остаются справедливыми и в случае кусочно гладкой линии Г (т. е. когда Г-объединение конечного числа гладких разомкнутых дуг, к-рые могут попарно пересекаться только по своим концам). С. и. у. исследованы также в функциональных пространствах Лебега L_p (Г).и L _р (Г ,r), где р>1, а r - нек-рый вес (см. [4] - [7]). В работах [4] - [6] приведены результаты, к-рые непосредственно обобщают выше сформулированные утверждения.

Пусть уравнение простой спрямляемой линии Г есть 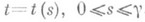, где s - дуга этой линии, отсчитываемая от нек-рой фиксированной точки на ней, g - длина Г. Говорят, что функция f, определенная на Г, почти всюду конечна, измерима, интегрируема и т. д., если функция f(t(s)).на сегменте [0, g] обладает соответствующим свойством. Интеграл Лебега от f на Г определяют равенством

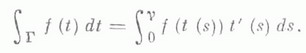
Через L_p (Г).обозначается множество измеримых на Г функций таких, что |f|^p интегрируема на Г. Функциональный класс 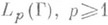, превращается в банахово пространство, если норму элемента f определить равенством

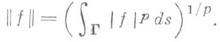
Если в уравнениях (3), (7), в к-рых равенства соблюдаются почти всюду, коэффициенты a, b непрерывны и удовлетворяют условию нормальности, , p>1, то остаются в силе утверждения 1) и 2), если в них класс Нзаменить классом L _р (Г), р>1. Далее, если решения уравнения K_j=f, где оператор Кимеет вид (2), разыскиваются в банаховом пространстве L_p (Г), р>1, а решения союзного однородного сним уравнения K'y=0 - в пространстве L _Р' (Г), где р'=р/( р-1), то остаются в силе и теоремы Нётера, причем Vможет быть любым вполне непрерывным оператором в L_p (Г).

Когда Г является конечной совокупностью разомкнутых линий или Г замкнута, но коэффициенты С. и. у. терпят разрывы, то решения уравнений часто разыскиваются в весовых функциональных пространствах

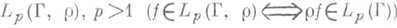. При определенных условиях относительно весовой функции р остаются справедливыми результаты, аналогичные вышеприведенным .

Задача регуляризации. Одной из основных задач, возникающих при построении теории С. и. у., является задача регуляризации, т. е. задача приведения С. и. у. к уравнению Фредгольма.

Пусть Еи Е ₁ - банаховы пространства, к-рые могут и совпадать, А - линейный ограниченный оператор . Ограниченный оператор В наз. левым регуляризатором оператора. A, если BA=I+V, где I, V - тождественный и вполне непрерывный операторы в Е. Если уравнения Aj=f и ВАj=Bf эквивалентны, каков бы ни был элемент 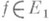, то Вназ. левым эквивалентным регуляризатором оператора А. Ограниченный оператор Вназ. правым регуляризатором оператора А, если AB=I₁+V₁, где I₁, V₁ - тождественный и вполне непрерывный операторы в E₁ соответственно. Если при любом 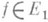уравнения Aj=f и ABy=f одновременно разрешимы или неразрешимы, причем в случае разрешимости между их решениями существует связь j=By, то Вназ. правым эквивалентным регуляризатором оператора A. Если В является одновременно левым и правым регуляризатором оператора А, то его наз. двусторонним регуляризатором, или просто регуляризатором, оператора A. Говорят, что оператор Адопускает регуляризацию левую, правую, двустороннюю, эквивалентную, если существует его регуляризатор (соответственно левый, правый, двусторонний, эквивалентный).

Пусть К - оператор, определяемый равенством (2), где Г- замкнутая простая гладкая линия, а, b суть H-функции (или непрерывные функции), удовлетворяющие условию нормальности, V - вполне непрерывный оператор в пространстве L_p (Г), р>1. Тогда в этом последнем пространстве оператор Кимеет бесчисленное множество регуляризаторов, среди к-рых находится, напр., оператор

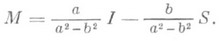
Для того чтобы оператор Кдопускал левую эквивалентную регуляризацию, необходимо и достаточно, чтобы индекс 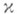оператора Кбыл неотрицательным [7]. В качестве эквивалентного левого регуляризатора можно взять оператор М. Если , то оператор Кдопускает правую эквивалентную регуляризацию, к-рую можно осуществить с помощью оператора М(см. [1]).

Системы С. и. у. Если в (1) а, b, k - квадратные матрицы ге-го порядка, рассматриваемые как матрицы линейных преобразований искомого вектора j=(j₁,. . ., j_n), а f=(f₁, . . ., f_n) - известный вектор, то (1) наз. системой С. и. у. Система (1) наз. нормального тина, если матрицы А=а+b и В=а-b неособенные на Г, то есть .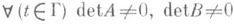

Теоремы Нётера остаются в силе для системы С. и. у. в классе Н(см. [1], [3]) и обобщаются на случай функциональных пространств Лебега (см. [4], [5]). В отличие от одного уравнения характеристич. системы С. и. у. в общем случае не решаются в квадратурах, но для вычисления индекса и в этом случаен айдена (см. [1]) формула, аналогичная формуле (9):

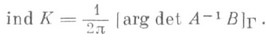
В случае системы С. и. у. задачи регуляризации (см. [3]) аналогичны задачам регуляризации для одного С. и. у.

В различных постановках исследованы как одно С. и. у., так и их системы, когда нарушаются условия нормальности (см. [11] и указанную там библиографию) .

Многомерные С. и. у. Так называются уравнения вида

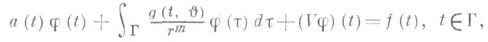
(11)

где Г - область евклидова пространства Е _т, m>1; Г может быть конечной или бесконечной, в частности может совпасть с Е _т; t,t; - точки пространства Е _т, r=|t-t|, J=(t-t)/r, dt-элемент объема в пространстве Е _т, V - вполне непрерывный оператор в банаховом функциональном пространстве, в к-ром ищется решение j; a, g - заданные функции; несобственный сингулярный интеграл понимается в смысле главного значения, т. е.

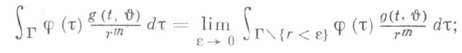(12)

точка tназ. полюсом, функция g(t,J). -характеристикой, функция j - плотностью сингулярного интеграла (12). Предел в равенстве (11), как правило, не существует, если не выполняется условие

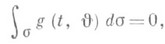(13)

где s - единичная сфера с центром в начале координат. Поэтому условие (13) всегда предполагается выполненным.

В теории многомерных С. и. у. важную роль играет понятие символа сингулярного оператора А, к-рый строится с помощью функций a, g, причем по данному символу сингулярный оператор восстанавливается с точностью до вполне непрерывного слагаемого. Композиции сингулярных операторов соответствует произведение их символов. Доказано [7], что при нек-рых ограничениях уравнение (11) допускает регуляризацию в пространстве L_p, р>1, тогда и только тогда, когда модуль его символа имеет положительную нижнюю грань и в этом случае справедливы теоремы Фредгольма.

Историческая справка. Исследование одномерных С. и. у. было начато почти одновременно с построением теории Фредгольма уравнения в работах Д. Гильберта (D. Hilbert) и А. Пуанкаре (A. Poincare). В одном частном случае С. и. у. с ядром Коши было рассмотрено гораздо раньше в докторской диссертации Ю. В. Сохоцкого, опубликованной в Петербурге в 1873; однако это исследование осталось незамеченным.

Основополагающие результаты по построению общей теории уравнения (1), (10) были получены в нач. 20-х гг. 20 в. Ф. Нётером [9] и Т. Карлеманом [10]. Ф. Нётер впервые ввел понятие индекса и доказал сформулированные выше теоремы 1-3 с помощью применения способа левой регуляризации. Этот способ впервые был указан (в различных частных случаях) А. Пуанкаре и Д. Гильбертом, но в общем виде он появляется именно у Ф. Нётера. Основным моментом в реализации упомянутого способа является применение формулы перестановки (композиции) в повторных сингулярных интервалах в смысле главного значения по Коши (Пуанкаре - Бертрана формула). Т. Карлеман для нек-рых частных классов уравнения (3) дал основную идею метода редукции этого уравнения к следующей граничной задаче теории аналитических функций (задача линейного сопряжения, см. [1]):

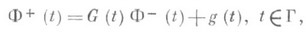
и указал путь построения явного решения. Т. Карлеману и И. Н. Векуа принадлежит способ регуляризации уравнения (1) с привлечением решения характеристич. уравнения (3).

Большое теоретическое и прикладное значение С. и. у. особенно проявилось с кон. 30-х гг. в связи с решением нек-рых весьма важных задач механики сплошной среды (теории упругости, гидро- и аэромеханики и др.) и теоретич. физики. Теория одномерных С. и. у. была значительно продвинута в 40-х гг. и получила в определенном смысле законченный вид в трудах советских математиков. Изложение такой теории одномерных С. и. у. в гёльдеровых классах функций дано в монографии одного из создателей этой теории Н. И. Мусхелишвили (см. [1]). Эта монография стимулировала научные исследования и в нек-рых других направлениях, напр. в теории С. и. у., не удовлетворяющих условию нормальности по Хаусдорфу, С. и. у. с недиагональными особенностями (со смещениями), уравнений Винера - Хопфа, многомерных С. и. у. и т. д. Первые исследования по многомерным С. и. у. принадлежат Ф. Трикоми (F. Tricomi, 1928), к-рый установил формулу перестановки двумерных сингулярных интегралов и применил ее к решению одного класса С. и. у. В этом направлении фундаментальное исследование принадлежит Ж. Жиро (G. Giraud, 1934), доказавшему справедливость теорем Фредгольма для нек-рых классов многомерных С. и. у. на ляпуновских многообразиях.

Лит.:[1] Мусхелишвили Н. И., Сингулярные интегральные уравнения, 3 изд., М., 1968; [2] Гахов Ф. Д., Краевые задачи, 3 изд., М., 1977; [3] Векуа Н. П., Системы сингулярных интегральных уравнений и некоторые граничные задачи, 2 изд., М., 1970; [4] Хведелидзе Б. В., "Тр. Тбилисск. матем. ин-та АН Груз. ССР", 1956, т. 23, с. 3-158; [5] Данилюк И. И., Нерегулярные граничные задачи на плоскости, М., 1975; [6] Гохберг И. Ц., Крупник Н., Введение в теорию одномерных сингулярных интегральных операторов, Киш., 1973; [7] Михлин С. Г., Многомерные сингулярные интегралы и интегральные уравнения, М., 1962; [8] Бицадзе А. В., Краевые задачи для эллиптических уравнений второго порядка, М., 1966: [9] Nоеthеr F., "Math. Ann.", 1921, Bd 82, S. 42-63; [10] Саrlemаn Т., "Arkiv mat., astron. och fys.", 1922, Bd 16, № 26, S. 1-19; [1l] Пресдорф 3., Некоторые классы сингулярных уравнений, пер. с нем., М , 1979 А. В. Бицадзе, Б. В. Хведелидзе.