Akademik

- одно из основных понятий математического анализа.

Пусть действительная функция f определена на нек-ром подмножестве Едействительных чисел , т. е. 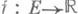. Функция f наз. непрерывной в точке (или, подробнее, непрерывной в точке по множеству Е), если для любого числа 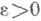существует такое число 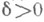, что для всех точек , удовлетворяющих условию 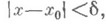выполняется неравенство

Если обозначить

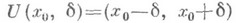
и

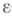соответственно и -окрестности точек и , то данное определение можно перефразировать следующим образом: функция f наз. непрерывной в точке 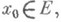если для любой 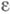-окрестност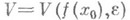и точки 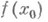существует такая -окрестность 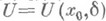точки , что

Используя понятие предела, можно сказать, что функция /непрерывна в точке х ₀ , если в этой точке существует ее предел по множеству Еи этот предел равен :

Это равносильно тому, что

где т. е. бесконечно малому приращению аргумента в точке х ₀ соответствует бесконечно малое приращение функции.

В терминах предела последовательности определение Н. ф. в точке : функция fнепрерывна в точке , если для любой последовательности точек

имеет место

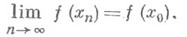
Все приведенные определения Н. ф. в точке эквивалентны между собой.

Если функция f непрерывна в точке по множеству (соответственно по множеству ), то функция наз. непрерывной справа (слева) в точке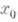

Все основные элементарные функции являются непрерывными во всех точках их областей определения. Важным свойством Н. ф. является замкнутость класса непрерывных функций относительно арифметич. операций и операции композиции функций. Более точно, если действительные функции , непрерывны в точке 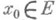, то их сумма 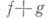и произведение , а при и частное 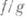(заведомо определенное в пересечении нек-рой окрестности точки х ₀ с множеством Е)непрерывны в точке х ₀. Если, как и выше, функция непрерывна в точке а функция такова, что и, следовательно, имеет смысл композиция , причем существует такое 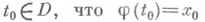и функция непрерывна в точке t₀, то композиция также непрерывна в точке t₀. Таким образом, в этом случае

т. е. в этом смысле операция предельного перехода перестановочна с операцией взятия Н. ф. Из перечисленных свойств Н. ф. следует, что не только основные, но и любые элементарные функции непрерывны в области их определения. Сохраняется свойстве непрерывности и при равномерном предельном переходе: если последовательность функций равномерно сходится на множестве Еи каждая функция 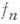непрерывна в точке то и предельная функция непрерывна в этой точке.

Если функция непрерывна в каждой точке множества Е, то она наз. непрерывной на множестве Е. Если и функция f непрерывна в точке х ₀, то сужение функции f на множестве Е' также непрерывно при . (Обратное, вообще говоря, неверно. Напр., сужение Дирихле функции как на множестве рациональных, так и иррациональных точек непрерывно, а сама функция Дирихле разрывна во всех точках.

Важный класс действительных Н. ф. одного переменного образуют функции, непрерывные на отрезках. Они обладают следующими свойствами.

Первая теорема Вейерштрасса: функция, непрерывная на отрезке, ограничена на нем.

Вторая теорема Вейерштрасса: функция, непрерывная на отрезке, принимает на нем наибольшее и наименьшее значения.

Теорема Коши о промежуточных значениях: функция, непрерывная на отрезке, принимает на нем любое значение, заключенное между значениями, к-рые она принимает на концах отрезка.

Теорема об обратной функции: если функция непрерывна и строго монотонна на отрезке, то у нее существует однозначная обратная функция, к-рая также определена на нек-ром отрезке, строго монотонна и непрерывна на нем.

Теорема Кантора о равномерной непрерывности: функция, непрерывная на отрезке, равномерно непрерывна на нем.

Всякая функция, непрерывная на отрезке, может быть равномерно сколь угодно точно приближена алгебраич. многочленом, а всякая функция f, непрерывная на отрезке и такая, что может быть равномерно сколь угодно точно приближена тригонометрич. полиномами (см. Вейерштрасса теорема о приближении функций).

Понятие Н. ф. обобщается на более общие виды функций, прежде всего на функции многих переменных. Сформулированное выше определение Н. ф. формально сохраняется, если под Епонимать подмножество и-мерного евклидова пространства 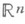, под 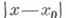- расстояние в этом пространстве между точками и , под - -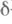окрестность в точки 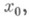а под

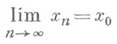
понимать предел последовательности точек в пространстве 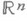. Функция , многих переменных непрерывная в точке наз. также непрерывной в этой точке по совокупности переменных в отличие от функций многих переменных, непрерывных по отдельным переменным. Функция 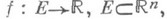наз. непрерывной в точке х ₀, напр., п о переменной х ₁ , если в точке 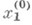непрерывно сужение функции f на множестве

т. е. в точке непрерывна функция 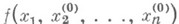одного переменного . Функция 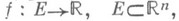, может быть непрерывной в точке хпо каждому переменному но может не быть непрерывной в этой точке по совокупности переменных. Определение Н. ф. непосредственно переносится на комплекснозначные функции. Следует лишь в данном выше определении под понимать абсолютную величину комплексного числа , а под

- предел в комплексной плоскости.

Все эти определения являются частным случаем более общего понятия Н. ф. f, областью определения которой является некоторое топологическое пространство Xи значения которой принадлежат некоторому топологическому пространству Y (см. Непрерывное отображение).

На непрерывные отображения топологич. пространств переносятся многие свойства действительных Н. ф. одного переменного. Обобщение упомянутых выше теорем Вейерштрасса: непрерывный образ бикомпактного топологич. пространства в хаусдорфовом топологич. пространстве является бикомпактом. Обобщение теоремы Коши о промежуточных значениях непрерывной на отрезке функции: непрерывный образ в топологич. пространстве связного топологич. пространства также связен. Обобщение теоремы о функции, обратной к непрерывной строго монотонной функции: взаимно однозначное непрерывное отображение бикомпакта на топологич. хаусдорфово пространство есть гомеоморфизм. Обобщение теоремы о пределе равномерно сходящейся последовательности непрерывных функций: если -равномерно сходящаяся последовательность непрерывных в точке отображений топологич. пространства Xв метрич. пространство Y, то предельное отображение 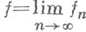также непрерывно в точке x₀.

Обобщением теоремы Вейерштрасса о приближении функций непрерывных на отрезке многочленами является Вейерштрасса- Стоуна теорема.

Лит.:[1] Александров П. С, Введение в теорию множеств и общую топологию, М., 1977; [2] Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 5 изд., М., 1981; [3] Никольский С. М., Курс математического анализа, 2 изд., т. 1-2, М., 1975; [4] Ильин В. А., Позняк Э. Г., Основы математического анализа, 3 изд., ч. 1, М., 1971. Л. Д. Кудрявцев,