Akademik

- линейная дифференциальная форма в на главном расслоенном пространстве Р, к-рая принимает значения в алгебре gструктурной группы Gпространства Р, определяется нек-рой линейной связностью Г в Р и сама определяет эту связность однозначно. По связности Г значение С. ф. q_y (Y), где 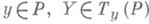, определяется как тот элемент в g,к-рый в действии Gна Рпорождает вторую компоненту вектора Yотносительно прямого расслоения Т _y (Р)=, где G _у- слой, содержащий у, а - горизонтальное распределение связности Г. По С. ф. q горизонтальное распределение , а тем самым и связность Г, восстанавливается следующим образом.

Т е о р е м а К а р т а н а - Л а п т е в а. Чтобы нек-рая форма q на Р со значениями в g была С. ф., необходимо и достаточно следующее: 1) при 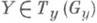значением q_y (Y)является тот элемент в g, к-рый в действии G на Р порождает Y,2) g- значная 2-форма

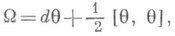
составленная из q, является полубазовой, или горизонтальной, т. е. 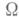_у(Y, Y')=0, если хотя бы один из векторов Y и Y' принадлежит Т _y(G _у).2-форма 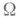наз. кривизны формой связности. Если в g задан базис {е _1;. . ., е _r}, то условие 2) выражается локально в виде равенств:

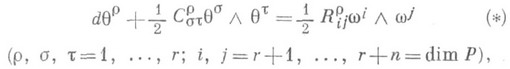
где w¹,. . ., wⁿ - нек-рые линейно независимые полубазовые 1-формы. В такой форме необходимость условия 2) установил Э. Картан [1]; его достаточность при выполнении условия 1) доказал Г. Ф. Лаптев [2]. Уравнения (*) на компоненты С. ф. наз. структурными уравнениями связности в Р, в них 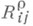составляют о б ъ е к т к р и в и з н ы.

Пусть Р, в качестве примера, является пространством аффинных реперов в касательных пространствах n-мерного гладкого многообразия М. Тогда Gи g являются соответственно группой и алгеброй Ли матриц вида

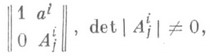И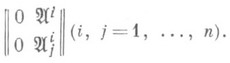

В силу теоремы Картана - Лаптева g-значная 1-форма

на Р является С. ф. нек-рой аффинной связности на Мтогда и только тогда, когда

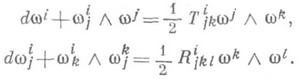
Здесь и 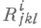составляют соответственно тензор кручения и тензор кривизны аффинной связности на М. Последние два уравнения на компоненты С. ф. наз. структурными уравнениями полученной на Маффинной связности.

Лит.:[1] C a r t a n Е., "Acta math.", 1926, v. 48, р.1-42; [2]| Л а п т е в Г. Ф., "Тр. Моск. матем. об-ва", 1953, т. 2, с. 275-382; [3] К о б а я с и Ш., Н о м и д з у К., Основы дифференциальной геометрии, т. 2, пер., с англ., М., 1981.

Ю. Г. Лумисте.