Akademik

на расслоенном пространстве - дифференциально-геометрическая структура на гладком расслоенном пространстве со структурной группой Ли, обобщающая связности на многообразии, в частности, напр., Леви-Чивита связность в римановой геометрии. Пусть является гладким локально тривиальным расслоением, на типовом слое Fк-рого эффективно и гладко действует группа Ли G. С. в этом расслоении - это отображение категории кусочно гладких кривых базы Вв категорию диффеоморфизмов слоя на слой, к-рое кривой L=L(x₀, х₁). с началом х ₀ и концом х ₁ сопоставляет диффеоморфизм и удовлетворяет следующим аксиомам:

1) при и справедливы

2) при произвольном тривиализующем диффеоморфизме и при диффеоморфизм , где ,

определяется действием нек-рого элемента ;

3) для нек-рой кусочно гладкой параметризации отображение , где

L_t - образ отрезка [0, t]при l, определяет кусочно гладкую кривую в G, начинающуюся в единице , причем и с общим ненулевым касательным вектором определяют пути в G с общим касательным вектором , гладко зависящим от x₀ и X.

Диффеоморфизм ГLназ. параллельным перенесением вдоль L. Параллельные перенесения вдоль всевозможных замкнутых кривых L(х ₀, х₀ )составляют голономии группу связности Г в точке х ₀, изоморфную нек-рой подгруппе Ли в G, независящей от х ₀. Кривая

(у ₀, у ₁ )в Еназ. горизонтальной для связности Г, если для любого при нек-рой ее кусочно гладкой параметризации. Если заданы L(x₀, х₁ )и , то всегда существует единственная горизонтальная , наз. горизонтальным п о д н я т и е м кривой L, такая, что ; она состоит из . Множество горизонтальных поднятий всех Lв Вопределяет связность Г однозначно: ГLотображает концы всех поднятий кривой Lв их начала.

С. наз. линейной, если q_j ( х, X )при произвольных j и хзависит от Xлинейно или, что равносильно, если для любой касательные векторы горизонтальных кривых с началом уобразуют в Т _у (Е)векторное подпространство , наз. горизонтальным подпространством. При этом , где F_y - слой, проходящий через у, то есть F_y=p^-1 (р(у)). Гладкое распределение 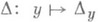наз. горизонтальным распределением линейной связности Г. Оно определяет Г однозначно: горизонтальными поднятиями являются его интегральные кривые.

Расслоенное пространство Еназ. главным (соответственно пространством однородного типа) и обозначается Р(соответственно Q), если Gдействует на Fпросто транзитивно (соответственно транзитивно), т. е. если для произвольных существует точно один (соответственно существует) элемент , к-рый переводит z в z'. Пусть Gдействует на Fслева; тогда на Ропределяется ее естественное правостороннее действие, в к-ром gопределяет . При этом Qотождествимо с фактормногоооразием P/H, составленном из орбит yo Н, где Н - стационарная подгруппа нек-рой точки из F=G/H. Общее Еотождествимо с фактормногообразием орбит относительно действия, определяемого формулой

Гладкое распределение на Рявляется горизонтальным распределением нек-рой линейной С. (к-рую оно определяет однозначно) тогда и только тогда, когда

для произвольных и . Все горизонтальные распределения на Q(соответственно Е).являются образами таких D при канонич. проекции (соответственно естественных поднятий таких на при канонич. проекции Часто линейная С. определяется прямо как распределение с указанными выше свойствами. Известно, что в каждом Р, а вместе с тем и в каждом Qи Е, существует нек-рая линейная С.

Исследование линейной С. в Р проводится обычно с помощью связности формы, к-рая определяет С. однозначно и может быть положена в основу еще одного ее определения. Важной ее характеристикой является кривизны форма, с помощью к-рой можно вычислить алгебру Ли группы голономии.

Впервые понятие С. возникло в 1917 в работе Т. Леви-Чивита [1] о параллельном перенесении вектора в римановой геометрии. Уже в 1918 Г. Вейль [2] дал понятие аффинной связности. В 20-е гг. Э. Картан (см. [3] - [5]) перешел к исследованию проективной связности и конформной связности, в 1926 дал общую концепцию "неголономного пространства с фундаментальной группой" (см. Связности на многообразии), где эти пространства освещены с точки зрения общей теории С. В 40-е гг. В. В. Вагнер развивал еще более общую концепцию, близкую по духу (но не по методу) к современному понятию С. Решающим был 1950, когда появились сводное изложение В. В. Вагнера [6], первые заметки Г. Ф. Лаптева, открывающие новые подходы, особенно в части аналитич. аппарата, и работа Ш. Эресмана [7], положившая начало современной глобальной теории С. См. также Вейля связность, Линейная связность, Риманова связность, Симплектическая связность, Эрмитова связность.

Лит.:[1] L e v i-C i v i t а Т., "Rend. circ. mat. Palermo", 1917, t. 2, p. 173-205; [2] W e y l H., Raum, Zeit, Materie,

5 Aufl., В., 1923; [3] C a r t a n E., "Ann. Soc. pol. math.", 1923, t. 2. p. 171-221; [4] е г о ж е, "Bull. Soc. math, de France", 1924 t. 52, p. 205-41; [5] e г о ж е, "Acta math.", 1926, t. 48, p. 1-42; [6] В а г н е р В. В., "Тр. Семин, по вект. и тенз. анализу", 1950, в. 8, с. 11-72; [7] E h r e s m a n n С., в кн.: Coll. de Topologie. Bruxelles, 1950, P., 1951, p. 29-55; [8] Л а п т е в Г. Ф., "Тр. Моск. матем. об-ва", 1953, т. 2, с. 275-382;[9] Н о м и д з у К., Группы Ли и дифференциальная геометрия, пер. с англ., М., 1960; [10] Л и х н е р о в и ч А., Теория связностей в целом и группы голономий, пер. с франц., М., 1960; [11] Л у м и с т е Ю. Г., в кн.: Итоги науки. Сер. Математика, в. 21 - Алгебра. Топология. Геометрия. 1969, М., 1971, с. 123-68. Ю. Г. Лумисте.