на векторном пространстве Vнад нолем k - элемент tвекторного пространства

где V*=Hom(V, k) - пространство, сопряженное с V. Говорят, что тензор tявляется рраз контравариантным и qраз ковариантным или что tимеет тип ( р, q). Число р наз. контравариантной валентностью, q - ковариантной валентностью, а число р+q - общей валентностью тензора t. Пространство Т 0,0(V)отождествляется с k. Тензоры типа ( р,0) наз. контравариантными, типа (0, q) - ковариантными, а остальные - смешанными.
Примеры Т.
1) Вектор пространства V(Т. типа , (1,0)).
2) Ковектор пространства V(Т. типа (0, 1)).
3) Каждый ковариантный Т.

где 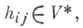 определяет q-линейную форму
определяет q-линейную форму  на Vпо формуле
на Vпо формуле

отображение  пространства Т 0,q в пространство Lq(V) всех q-линейных форм на Vлинейно и инъектив-но; если dim
пространства Т 0,q в пространство Lq(V) всех q-линейных форм на Vлинейно и инъектив-но; если dim  то это отображение является изоморфизмом, так что любая q-линейная форма отвечает нек-рому Т. типа (0, q).
то это отображение является изоморфизмом, так что любая q-линейная форма отвечает нек-рому Т. типа (0, q).
4) Аналогично, каждый контравариантный Т. из Т р,0(V)определяет нек-рую р-линейную форму на V*, а если Vконечномерно, то верно и обратное.
5) Каждый Т.

где  определяет линейное преобразование
определяет линейное преобразование  пространства V, заданное формулой
пространства V, заданное формулой

если 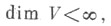 то любое линейное преобразование пространства Vопределяется Т. типа (1, 1).
то любое линейное преобразование пространства Vопределяется Т. типа (1, 1).
6) Аналогично, любой Т. типа (1, 2) определяет в Vбилинейную операцию, т. е. структуру k-алгебры; при этом, если dim  то любая структура k-алгебры в Vопределяется век-рым Т. типа (1, 2), к-рый наз. структурным тензором алгебры.
то любая структура k-алгебры в Vопределяется век-рым Т. типа (1, 2), к-рый наз. структурным тензором алгебры.
Пусть Vконечномерно и v1, . .., vn - его базис, v1, . . ., vn - сопряженный базис пространства V*. Тогда Т.

составляют базис пространства Tp,q (V). Координаты  тензора
тензора 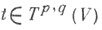 в этом базисе наз. также к о-ординатами тензора tвбазисе v1, . . ., vn пространства V. Напр., координаты вектора и ковектора совпадают с их обычными координатами в базисах
в этом базисе наз. также к о-ординатами тензора tвбазисе v1, . . ., vn пространства V. Напр., координаты вектора и ковектора совпадают с их обычными координатами в базисах  и
и  , координаты Т. типа (0, 2) совпадают с элементами матрицы соответствующей билинейной формы, координаты Т. типа (1, 1) - с элементами матрицы соответствующего линейного преобразования, координаты структурного Т. алгебры - с ее структурными константами. Если
, координаты Т. типа (0, 2) совпадают с элементами матрицы соответствующей билинейной формы, координаты Т. типа (1, 1) - с элементами матрицы соответствующего линейного преобразования, координаты структурного Т. алгебры - с ее структурными константами. Если  - другой базис пространства
- другой базис пространства  то координаты
то координаты  тензора tв этом базисе определяются по формулам
тензора tв этом базисе определяются по формулам 
Здесь, как это часто делается в тензорном исчислении, применимо правило суммирования Эйнштейна: по каждой паре одинаковых индексов, один из к-рых - верхний, а другой - нижний, подразумевается суммирование от 1 до п. Обратно, если система п p+q элементов поля k, зависящая от базиса пространства V, изменяется при переходе от базиса к базису по формулам (1), то эта система является набором координат нек-рого Т. типа ( р, q).
В векторном пространстве Т p,q (V)определены операции сложения Т. и умножения Т. на екаляр из k. При этих операциях соответствующие координаты Т. складываются или умножаются на скаляр. Определена также операция умножения Т. разных типов, к-рая вводится следующим образом. Имеет место естественный изоморфизм векторных пространств

переводящий

в 
Поэтому для любых 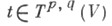 и
и 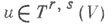 элемент
элемент  может рассматриваться как Т. типа (p+r, q+s), к-рый и наз. произведением тензоров tи и. Координаты произведения вычисляются по формуле
может рассматриваться как Т. типа (p+r, q+s), к-рый и наз. произведением тензоров tи и. Координаты произведения вычисляются по формуле
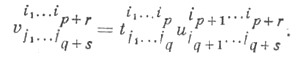
Пусть р>0, q>0 и пусть фиксированы числа  и
и 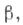 где
где  Тогда определено линейное отображение
Тогда определено линейное отображение

такое, что

Оно наз. свертыванием (или сверткой) по  -му контравариантному и
-му контравариантному и 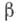 -му ковариантному индексам. В координатах свертка записывается формулами
-му ковариантному индексам. В координатах свертка записывается формулами

Напр., свертка 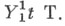 типа (1, 1) есть след соответствующего линейного преобразования.
типа (1, 1) есть след соответствующего линейного преобразования.
Аналогично определяются Т. на произвольном унитарном модуле Vнад коммутативно-ассоциативным кольцом с единицей. Перечисленные выше примеры и свойства Т. переносятся с соответствующими изменениями на этот случай, причем иногда надо предполагать, что V- свободный или конечно порожденный свободный модуль.
Пусть в конечномерном векторном пространстве над полем kфиксирована невырожденная билинейная форма g(напр., V - евклидово или псевдоевклидово пространство над 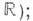 форму gназывают в этом случае метрическим тензором. Метрический Т. определяет изоморфизм
форму gназывают в этом случае метрическим тензором. Метрический Т. определяет изоморфизм  по формуле
по формуле
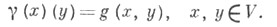
Пусть р>0 и пусть фиксирован индекс  Тогда формула
Тогда формула
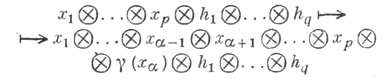
определяет изоморфизм  называемый опусканием
называемый опусканием  -го контравариантного индекса. Иначе,
-го контравариантного индекса. Иначе,

В координатах опускание индекса имеет вид

Аналогично определяется изоморфизм подъема  -го ковариантного индекса
-го ковариантного индекса 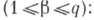
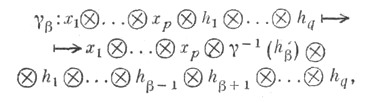
отображающий  на
на  В координатах подъем индекса записывается формулой
В координатах подъем индекса записывается формулой
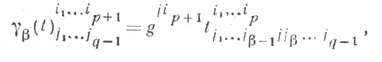
где 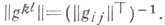 В частности, подъем сначала 1-го, а потом и оставшегося ковариантного индекса метрич. тензора gприводит к Т, типа (2, 0) с координатами gkll (контравариантный метрический тензор). Иногда опущенный (поднятый) индекс не передвигают на первое (последнее) место, а пишут на том же месте в нижней (верхней) группе индексов, ставя на образовавшемся пустом месте точку. Напр., для
В частности, подъем сначала 1-го, а потом и оставшегося ковариантного индекса метрич. тензора gприводит к Т, типа (2, 0) с координатами gkll (контравариантный метрический тензор). Иногда опущенный (поднятый) индекс не передвигают на первое (последнее) место, а пишут на том же месте в нижней (верхней) группе индексов, ставя на образовавшемся пустом месте точку. Напр., для  координаты Т.
координаты Т.  записывают в виде
записывают в виде

Любое линейное отображение  векторных пространств над k естественным образом определяет линейные отображения
векторных пространств над k естественным образом определяет линейные отображения

и 
Если f - изоморфизм, то определяется также линейное отображение

причем 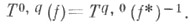 Соответствие
Соответствие  обладает функторными свойствами. В частности, оно определяет линейное представление
обладает функторными свойствами. В частности, оно определяет линейное представление  группы GL(V) в пространстве Tp,q(V)(тензорное представление).
группы GL(V) в пространстве Tp,q(V)(тензорное представление).
Лит.:[1] Бурбаки Н., Алгебра. Алгебраические структуры. Линейная и полилинейная алгебра, пер. с франц., М., 1962; [2] Гельфанд И. М., Лекции по линейной алгебре, 4 изд., М., 1971; [З] Кострикин А. И., Манин Ю. И., Линейная алгебра и геометрия, М., 1980; [4] Постниковы. М., Линейная алгебра и дифференциальная геометрия, М., 1979; [5] Рашевский П. К., Риманова геометрия и тензорный анализ, 3 изд., М., 1967.
А. Л. Онищик.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.