Akademik

топологическое пространство, в каждом открытом покрытии к-рого содержится конечное подпокрытие того же пространства. Следующие утверждения равносильны: 1) пространство Xбикомпактно; 2) пересечение любой центрированной системы замкнутых в Xмножеств не пусто; 3) пересечение любой максимальной центрированной системы замкнутых в Xмножеств не пусто; 4) пересечение произвольной убывающей вполне упорядоченной последовательности любой мощности непустых замкнутых в X множеств не пусто; 5) каждая центрированная система подмножеств множества Xимеет точку прикосновения в X; 6) каждый ультрафильтр на Xсходится в X;7) для каждого бесконечного подмножества Ммножества Xв Xсуществует точка полного накопления. Подпространство n-мерного евклидова пространства бикомпактно тогда и только тогда, когда оно замкнуто и ограничено. Понятие бикомпактного топологического пространства занимает фундаментальное положение в топологии и современном функциональном анализе; при этом нек-рые принципиальные свойства Б. п. (с многочисленными приложениями) рассматриваются уже в математическом анализе, например всякая непрерывная функция, определенная на Б. п., ограничена и принимает наибольшее ц наименьшее значения.

Термин "Б. п." принадлежит П. С. Александрову, внесшему огромный вклад в создание и развитие теории Б. п., начало к-рой положено "Мемуаром о компактных топологических пространствах" П. С. Александрова и П. С. Урысона.

Понятие бикомпактного пространства явилось первоначально усилением введенного М. Фреше (М. Frechet) понятия компактного пространства: топологич. пространство компактно - в первоначальном смысле слова, или счетно компактно, как говорят теперь) если в нем имеет место к.-л. из следующих эквивалентных между собою предложений: 1) в каждом счетном открытом покрытии этого пространства содержится его конечное подпокрытие; 2) пересечение любой счетной центрированной системы непустых замкнутых его подмножеств не пусто; 3) пересечение любой счетной убывающей последовательности непустых замкнутых множеств не пусто; 4) каждая счетная централизованная подмножеств множества система его подмножеств имеет точку прикосновения; 5) для каждого счетного подмножества в нем существует точка полного накопления.

Однако дальнейшее развитие математики и ее приложений показало, что понятие бикомпактности настолько важнее первоначального понятия компактности, что сейчас часто под компактностью понимают именно бикомпактность, а компактные в старом смысле пространства называют счетно компактными. Оба понятия равносильны в применении к метрическим пространствам.

Замкнутое подпространство Б. п. бикомпактно. Топологич. произведение любого множества Б. п. бикомпактно (теорема Тихонова, см. Тихоновское произведение). Топологич. пространство, являющееся образом Б. п. при непрерывном отображении, бикомпактно. Эти свойства Б. п. показывают устойчивость класса Б. и. по отношению к основным для общей топологии операциям, и на них в первую очередь базируются приложения понятия бикомпактности. Особое значение имеют Б. и., удовлетворяющие аксиоме отделимости Хаусдор-фа и на. з. бикомпактам и. При этом топологич. произведение любого множества бикомпактов есть бикомпакт; замкнутое подпространство бикомпакта является бикомпактом; образ бикомпакта при непрерывном отображении в хаусдорфово пространство есть бикомпакт. Далее перечисляются свойства бикомпактов, не имеющие места для произвольных Б. и. Каждый бикомпакт является нормальным и, тем более, вполне регулярным пространством. Пересечение любого счетного семейства открытых всюду плотных в бикомпакте множеств всюду плотно в нем. Равносильное утверждение: никакой бикомпакт нельзя представить в виде объединения счетного семейства нигде не плотных множеств. Бикомпакты характеризуются как регулярные пространства, замкнутые в любом объемлющем их ха-усдорфовом пространстве. На этом основана теорема о том, что каждое непрерывное отображение Б. п. в хаусдорфово пространство замкнуто. Эта теорема имеет важное следствие: любое взаимно однозначное непрерывное отображение Б. п. на хаусдорфово пространство есть гомеоморфизм.

Класс Б. п., равно как и класс бикомпактов, устойчив относительно перехода к пространству замкнутых подмножеств (взятому с топологией Вьеториса); при этом'вес пространства не повышается. Пространство непустых замкнутых подмножеств канторова совершенного множества Сгомеоморфно С. Особую роль в теории Б. п. играют тихоновские кубы.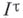 и обобщенные канторовы дисконтинуумы , определяемые соответственно как топологич. произведения отрезков [0,1] и как произведения простых двоеточий, где 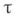- произвольное кардинальное число. При получаем гильбертов кирпич. Все являются бикомпактами и каждый бикомпакт веса, не превосходящего , гомеоморфен нек-рому замкнутому подпространству куба 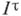Таким образом, каждый бикомпакт может быть получен из отрезков применением всего лишь двух операций: топологического произведения и перехода к замкнутому подпространству. Класс всех подпространств бикомпактов также допускает теперь точное описание - как класс всех подпространств кубов 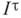. С другой стороны, это в точности класс всех вполне регулярных пространств.

Вес пространства - один из самых общих топологич. инвариантов - в случае бикомпактов становится особенно существенной характеристикой. Бикомпакт метризуем в том и только в том случае, если он обладает счетной базой. В то же время, если бикомпакт является образом процгранства Xпри непрерывном отображении, то вес не превышает веса X, т. е. среди непрерывных образов пространств со счетной базой нет неметрнзуемых бикомпактов. Вес бикомпакта 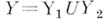не превосходит наибольшего из весов 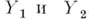, т. е. никакой неметризуемый бикомпакт нельзя представить в виде суммы двух пространств со счетной базой. В основе последних двух фактов лежит понятие сети. Если бикомпакт обладает сетью мощности 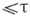, то он имеет и базу мощности . В частности, всякий счетный бикомпакт имеет счетную базу, метризуем и даже гомеоморфен замкнутому подмножеству отрезка. Обычно метризуемые бикомпакты наз. компактами. Всякая метрика на компакте полна и вполне ограничена, и каждое метризуемое пространство с этим свойством есть компакт (Ф. Хаусдорф, F. Hausdorff).

Топологич. произведение счетного еемейства компактов и замкнутые подмножества компактов суть компакты. Каждый нульмерный компакт гомеоморфен нек-рому компакту, лежащему в канторовом совершенном множестве (в качестве замкнутого подмножества). Всякий компакт есть непрерывный образ канторова совершенного множества (П. С. Александров). Каждый бикомпакт есть непрерывный образ нек-рого нульмерного бикомпакта.

В связи с важной ролью кубов 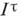в топологии был изучен класс бикомпактов, разлагающихся в произведение компактов, а также класс их непрерывных образов.

Бикомпакты, являющиеся непрерывными образами дисконтинуумов 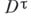, наз. диадическими. Класс диадич. бикомпактов достаточно широк: все компакты, все кубы , пространства всех бикомпактных топологич. групп суть диадич. бикомпакты. Класс диадич. бикомпактов есть наименьший класс топологич. пространств, замкнутый относительно топологич. произведений и непрерывных отображений и содержащий все бикомпакты, состоящие из конечного числа точек.

Простейшим примером недиадич. бикомпакта является несчетный бикомпакт с единственной неизолированной точкой. Диадич. бикомпакты обладают рядом замечательных свойств, напр.: всякая дизъюнктная система непустых открытых множеств диадич. бикомпакта конечна или счетна (свойство Суслина); всякий диадич. бикомпакт с первой аксиомой счетности метризуем, т. е. имеет счетную базу; произведение диадич. бикомпактов есть диадич. бикомпакт; бикомпакт, являющийся непрерывным образом диадич. бикомпакта, диадичен.

Специфич. свойствами обладают и упорядоченные бикомпакты. Связный сепарабельный упорядоченный бикомпакт обладает счетной базой. Примером связного сепарабельного (диадического) бикомпакта без счетной базы служит куб 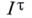при 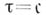(мощностьконтинуума). Каждый бикомпакт, являющийся непрерывным образом упорядоченного бикомпакта, имеет базу, границы элементов к-рой компакты. Пересечение класса диадич. бикомпактов с классом всех бикомпактов, являющихся непрерывными образами упорядоченных бикомпактов, состоит в точности из всех компактов.

Среди Б. п. важное место занимают совершенно нормальные бикомпакты. Нормальное пространство наз. совершенно нормальным, если каждое замкнутое в нем множество есть пересечение счетного семейства открытых множеств. Каждый совершенно нормальный бикомпакт обладает свойством Суслина. Любое пространство со счетной сетью, лежащее в совершенно нормальном бикомпакте, обладает счетной базой. Произведение даже двух совершенно нормальных бикомпактов может не быть совершенно нормальным бикомпактом: пространство будет совершенно нормальным бикомпактом в том и только в том случае, если X - компакт. Но образ совершенно нормального бикомпакта и произведение совершенно нормального бикомпакта на компакт совершенно нормальны. Бикомпакт совершенно нормален в том и только в том случае, если каждое его подпространство финально компактно. Проблема существования несепарабельного упорядоченного совершенно нормального бикомпакта эквивалентна Суслина проблеме.

Многие исследования посвящены выяснению связи между кардинальнозначными топологич. инвариантами для случая бикомпактов. Если база бикомпакта точечно счетна, то она счетна. Мощность любого несчетного бикомпакта с первой аксиомой счетности равна мощности континуума. Если бикомпакт секвенциален и удовлетворяет условию Суслина, то его мощность не превышает мощности континуума. Если однородный бикомпакт секвенциален, то 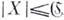. В специальном предположении построен наследственно сепарабельный бикомпакт мощности, большей, чем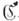

Имеется цикл теорем о бикомпактах, связанный с понятием универсальности (см. Универсальное пространство]. Для каждого кардинального числа 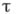существует такой бикомпакт веса 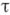, что каждый бикомпакт веса, не большего, чем , вкладывается в него посредством гомеоморфизма. Этим свойством обладает, напр., 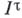. 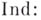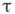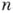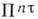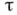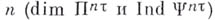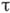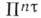Аналогичный результат имеет место для случая, когда фиксированы вес и размерность или каковы бы ни были кардинальное число и натуральное число , существуют такие бикомпакты, и веса и размерности , что каждый бикомпакт, вес к-рого не превосходит , а размерность не превосходит , вкладывается в (соответственно ) посредством гомеоморфизма. В качестве 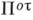и 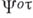можно взять 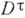. В предположении справедливости обобщенной континуум-гипотезы получен двойственный результат: для каждого кардинального числа существует нульмерный бикомпакт Xвеса 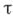, к-рый можно непрерывно отобразить на произвольный бикомпакт веса, не большего, чем .

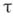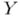Раздел общей топологии, посвященный непрерывным отображениям бикомпактов, является одним из самых разработанных и богатых результатами. Так, если и бикомпакты, а 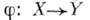непрерывное отображение и 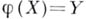, то существует замкнутое в Xподпространство , для к-рого и сужение 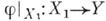является неприводимим отображением. Это выясняет фундаментальную роль неприводимых отображений. Для произвольного фиксированного бикомпакта Xво множеству 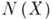всех бикомпактов Z, допускающих неприводимое отображение на X, существует бикомпакт 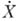, к-рый можно неприводимо отобразить на любой бикомпакт из 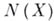. Этот бикомпакт 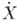наз. абсолютом бикомпакта X(см. Абсолют регулярного топологического пространства); он определен с точностью до гомеоморфизма. Бикомпакт тогда и только тогда гомео-морфен своему абсолюту, когда он экстремально несвязен (см. Экстремально несвязное пространство). Экстремально несвязных бикомпактов очень много: по каждому бикомпакту определяется его абсолют, являющийся экстремально несвязным бикомпактом. При этом неприводимые отображения бикомпактов определяются гомеоморфизмами их абсолютов. Они имеют весьма своеобразную структуру, в частности бесконечный экстремально несвязный бикомпакт всегда неоднороден. Два бикомпакта называются соабсолютны-ми, если их абсолюты гомеоморфны. Одной из общих задач здесь является отыскание эффективных внутренних критериев соабсолютности топологических пространств. Следует отметить, что естественная область действия теории абсолютов гораздо шире класса бикомпактов.

Неприводимые отображения важны не только в связи с понятием абсолюта. Известно (А. Н. Колмогоров), что каждое неприводимое отображение компакта на компакт имеет всюду плотное множество точек взаимной однозначности. Если диадич. бпкомпакт Xнеприводимо отображается на бикомпакт Yвеса , то вес Xравен .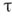

Важны также открытые отображения бикомпактов. Если два бесконечных бикомпакта связаны открытым конечнократным отображением, то их веса равны. Но существует открытое счетнократное отображение неметризуемого совершенно нормального бикомпакта на компакт. При этом каждое открытое счетнократное отображение бикомпакта на бикомпакт имеет всюду плотное множество точек локальной топологичности.

Бикомпакты много изучались в рамках теории размерности. Для любого бикомпакта Xимеет место 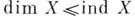(П. С. Александров). Существует бикомпакт 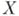с первой аксиомой счетности (а, следовательно, мощности, не превосходящей мощность континуума), для к-рого для всех совершенно нормальных бикомпактов.

Представляет интерес сопоставление теоремы о том, что открытые счетнократные отображения не повышают размерности бикомпактов, с теоремой о представлении: каждый бикомпакт положительной размерности есть образ нек-рого одномерного бикомпакта при открыто-замкнутом непрерывном отображении, в к-ром прообраз каждой точки нульмерен. 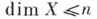Важное значение имеет факторизационная теорема: пусть - непрерывное отображение, - бикомпакты, и вес меньше или равен ; тогда существуют бикомпакт и непрерывные отображения 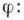меньше или равен .

Соотношениями между Б. п. и произвольными топо-логич. пространствами занимается теория бикомпактных расширений.

Лит.:[1] Александров П. С., Введение в общую теорию множеств и функций, М., 1948; [2] Александров П. С., Пасынков Б. А., Введение в теорию размерности, М., 1973; [3] Еngе1king R., Outline of General Topology, Amst., 1968; [4] Александров П. С., Урысон П. С., "Тр. Матем. ин-та АН СССР", 1950, т. 31, с. 1-96; [5] Александров П. С., "Матем. сб.", 1939, т. 5, в. 2, с. 403-24; 16] Архангельский А. В., "Докл. АН СССР", 1959, т. 126, № 2, с. 239-41; [7] его же, "Труды Моск. матем. об-ва", 1965, т. 13, с. 3-55; [8] его же, "Докл. АН СССР", 1969, т. 184, № 4, с. 767-71; [9] Мищенко А. С., там же, 1962, т. 144, № 5, с. 985-8; [10] Gleasоn A.M., "Illinois Math. J.", 1958, v. 2, № 4A, p. 482-9; [11] Архангельский А. В., "Докл. АН СССР", 1969, т. 187, №. 5, с. 967-70; [12] МаrdеsiсS., "Pacific 3.Math.", 1967, v. 23, № 3, p. 557- 568; [13] Колмогоров А. Н., "Докл. АН СССР", 1941, т. 30, №, с. 477-79; [14] Архангельский А. В., там же, 1967, т. 174, № 6, с. 1243-46; [15] Нanf W., "Math. Scand.", 1957, v. 5, № 2, p. 205-17. А. В. Архангельский.