Akademik

- непрерывное отображение топологич. пространства Xна топологич. пространство Y такое, что образ всякого замкнутого в Xмножества, отличного от X, отличен от Y. Если 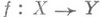- непрерывное отображение, причем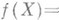 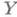и все прообразы точек при f бикомпактны, то существует замкнутое в Xподпространство Х ₁ такое, что 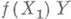и сужение f на Х ₁ является Н. о. Яркий эффект дает соединение требований неприводимости отображения и его замкнутости. Пространства, соединенные таким отображением, не отличимы по ряду важных характеристик: в частности, по числу Суслина и p-весу. Но главное значение замкнутым Н. о. дает центральная роль, к-рую они играют в теории абсолютов.

Лит.:[1J Архангельский А. В., Пономарев В. И., Основы общей топологии в задачах и упражнениях, М. 1974.

А. В. Архангельский.