Akademik

полугруппы - производная в нуле от полугруппы линейных ограниченных операторов 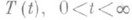, действующих в комплексном банаховом пространстве X. Если T(t).непрерывна по норме операторов, то она имеет вид T(t)= е ^tA0, где А ₀ - ограниченный оператор,

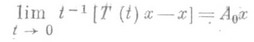(1)

при любом 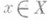и А ₀ есть П. о. T(t). Обратно, если предел слева существует при всех , то .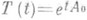

Более сложная картина возникает, когда Т(t).только сильно непрерывная полугруппа. В этом случае предел (1) существует не при всех х. Оператор А ₀, определенный на линейном множестве D(A₀).всех тех х, для к-рых предел существует, является линейным неограниченным оператором и наз. инфинитезимальным оператором. В частности, A₀ определен

на всех элементах вида

.

Если обозначить через Х ₀ замыкание объединения областей значений всех операторов Т(t), t>0, то D( А ₀).плотно в Х ₀ и, более того, 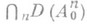плотно в Х ₀. Все значения оператора А ₀ также лежат в Х ₀. Если оператор А ₀ неограничен, то D(A₀).является множеством первой категории в Х ₀.

Если в Х ₀ нет элементов х, на к-рых 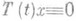, то оператор А ₀ допускает замыкание 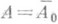, к-рое и наз. производящим оператором полугруппы Т(t). В этом случае при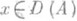

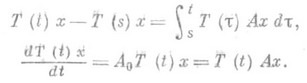(2)

Равенство (2) определяет замкнутый оператор А, к-рый, вообще говоря, шире, чем замыкание А ₀. Его иногда наз. обобщенным производящим оператором полугруппы Т(t).

На множестве D_R тех же 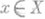, для к-рых сходится несобственный интеграл

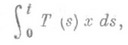(3) определен оператор

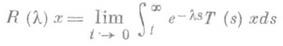
при Re l>w, где w - тип полугруппы Т(t). Этот оператор обладает свойствами:

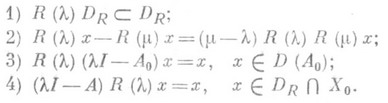
Если интеграл (3) абсолютно сходится при любом 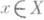, то П. о. Асуществует тогда и только тогда, когда из 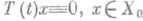, следует х=0;оператор R (l) ограничей, и, если Х ₀=Х, он совпадает о резольвентой оператора А; для того чтобы А ₀ был замкнутым ( А = А ₀), необходимо и достаточно, чтобы

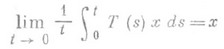
при любом .

Основной задачей теории полугрупп операторов является установление связи между свойствами полугрупп и свойствами их П. о., причем последние обычно формулируются в терминах операторов R(l).

Лит.:[1]Xилле Э., Филлипс Р., Функциональный анализ и полугруппы, пер. с англ., М., 1962; [2] Забрейко П. П., Зафиевский А. В., "Докл. АН СССР", 1969. т. 189, № 5, с. 934-37; [З] его ж е, там же, 1970, т. 195, № 1, с. 24-27. С. Г. Крейн.