Akademik

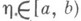- интеграл от неограниченной функции или от функции по неограниченному множеству. Пусть функция f определена на конечном или бесконечном полуинтервале , и для любого функция f интегрируема но Риману (по Лебегу) на отрезке 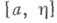Тогда предел

(в случае 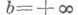условие понимается как ) наз. несобственным интегралом

Если предел (1) существует, то говорят, что Н. и. сходится, если не существует - расходится. Напр., Н. и.при сходится, а при расходится. Если же , то

сходится при и расходится при .

Если и функция f интегрируема по Риману (по Лебегу) на отрезке [ а, b], то Н. и. (1) совпадает с определенным интегралом.

Аналогично при соответствующих предположениях определяют Н. и. по промежутку

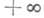
Если функция/ интегрируема по Риману (по Лебегу) на каждом отрезке и существуют то Н. и.

определяется как сумма

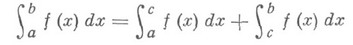
и не зависит от выбора точки с.

Если на интервале ( а, b )имеется конечное число точек

: таких, что функция f интегрируема по Риману (по Лебегу) на каждом отрезке , не содержащем ни одной точки 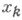, и для каждого существуют Н. и.

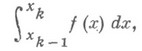
то Н. и.

Это определение не зависит от выбора точек .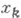

На Н. и. переносятся общие свойства интегралов: линейность, аддитивность относительно промежутков, по к-рым производится интегрирование, правило интегрирования неравенств, теоремы о среднем, интегрирование по частям и замены переменного, формула Ньютона - Лейбница. Напр., если функция f почти всюду на [ а, b )совпадает с производной функции F, к-рая абсолютно непрерывна на каждом отрезке то

Для выяснения сходимости Н. и. от знакопостоянных функций применяется признак сравнения: напр., для Н. и. вида (1) при выполнении условия

из сходимости Н. и.

следует сходимость Н. и.

функция наз. в этом случае функцией сравнения. В качестве функции сравнения для интегралов (1) в случае конечного предела интегрирования bчасто используются функции ; для интегралов вида (2) в случае конечности предела интегрирования а- функции , при наличии одного или двух бесконечных пределов интегрирования - функции 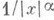. Из признака сравнения следует, напр., если для неотрицательной функции f, определенной при , существует предел

то пр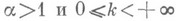и Н. и.

вида (1) сходится, а при Н. и. расходится.

Необходимое и достаточное условие сходимости Н. и. дает критерий Коши. Так, Н. и. вида (1) сходится тогда и только тогда, когда для любого 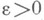существует такое что для всех выполняется неравенство

-

Н. и.

наз. абсолютно сходящимся, если сходится Н. и.

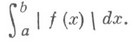
Если Н. и, абсолютно сходится, то он сходится и совпадает с интегралом Лебега. Существуют Н. и. сходящиеся, но не абсолютно. Напр., для конечного промежутка Н. и.:

а для бесконечного:

Существуют различные признаки для установления сходимости Н. и. Так, если функции f и gопределены для , функция f имеет на полуоси ограниченную первообразную, a g- монотонная функция, стремящаяся к нулю при то Н. и.

сходится. Другой признак: если Н. и.

сходится, а функция gмонотонна и ограничена при , то Н. и.

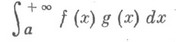
сходится.

Сходимость Н. и. можно выразить в терминах сходящихся рядов: напр., для того чтобы Н. и. (1) сходился, необходимо и достаточно, чтобы для любой последовательности сходился ряд

причем в случае его сходимости сумма ряда совпадает с Н. и. (1).

Понятие Н. и. обобщается для функций многих переменных. Пусть функция f определена на открытом (ограниченном или неограниченном) множестве G n -мерного евклидова пространства и интегрируема по Риману на любом измеримом по Жордану множестве Функцию f наз. интегрируемой в несобственном смысле по множеству G, если для любой последовательности измеримых по Жордану множеств таких, что 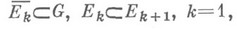существует предел

не зависящий от выбора указанной последовательности 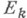. Этот предел, если он существует, наз. Н. и.

и, как в одномерном случае, говорят, что этот интеграл сходится. Он существует тогда и только тогда, когда существует интеграл

В этом случае Н. и.

совпадает с интегралом Лебега. Это обстоятельство связано с тем, что при n=1 и данном выше определении Н. и. переход к пределу осуществлялся по весьма специальному классу измеримых по Жордану множеств, а именно по отрезкам. В качестве же 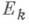были взяты произвольные измеримые по Жордану множества. Впрочем, при сделанное утверждение остается в силе и в том случае, когда в качестве множеств взяты только измеримые по Жордану области. Таким образом, в этом случае понятие Н. и. не приводит к новому понятию по сравнению с интегралом Лебега.

Для Н. и. от функции многих переменных справедлив признак сравнения, аналогичный одномерному случаю. В качестве интегралов сравнения берут

где

Первый сходится при и расходится при , второй сходится при и расходится при .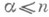

К Н. и. относятся интегралы в смысле главного значения. Пусть функция f определена на открытом множестве , кроме, быть может, точки , и пусть для любого функция f интегрируема (по Риману или по Лебегу) на множестве есть 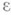-окрестность точки х. Тогда если существует предел

то его наз. интегралом в смысле главного значения и обозначают

Если интеграл

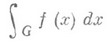
существует как Н. и., то он существует и в смысле главного значения. Обратное, вообще говоря, неверно. Напр., Н. и. расходится, а

Аналогично определяют интегралы в смысле главного значения в бесконечно удаленной точке.

Лит.:[1] Ильин В. А., Позняк Э. Г., Основы математического анализа, т. 2, М., 1973; [2] Кудрявцев Л. Д., Курс математического анализа, т. 2, М., 1981; [3] Никольский С. М., Курс математического анализа, 2 изд., т. 2, М., 1975.

Л. Д. Кудрявцев.